初识“回溯算法”讲解及LeetCode对应例题解析
- 回溯算法
- 1、回溯算法的概念
- 2、回溯算法的一般解题思路
- 3、解决问题的方法
- 例题一:二叉树中和为某一值的路径
- (1)题目描述
- (2)题目分析
- (3)代码实现
- 例题二:电话号码的字母组合
- (1)题目描述
- (2)题目分析
- (3)代码实现
回溯算法
1、回溯算法的概念
xxxx回溯算法也叫试探法,它是一种系统地搜索问题的解的方法。回溯算法的基本思想是:从一条路往前走,能进则进,不能进则退回来,换一条路再试。
xxxx上述文字有些抽象,如果将其具化来说。回溯法思路的具体描述是:把问题的解空间转化成了图或者树的结构表示,然后使用深度优先搜索策略进行遍历,遍历的过程中记录和寻找所有可行解或者最优解。
2、回溯算法的一般解题思路
1、定义一个解空间,它包含问题的解。
2、利用适于搜索的方法组织解空间。
3、利用深度优先法搜索解空间。
4、利用限界函数避免移动到不可能产生解的子空间。
注:问题的解空间通常是在搜索问题的解的过程中动态产生的,这是回溯算法的一个重要特性
3、解决问题的方法
xxxx对于常见的问题,既然我们将其解空间转化为了多叉树的深度优先遍历(DFS)/后序遍历,那么我们最常用的方法就是递归!!
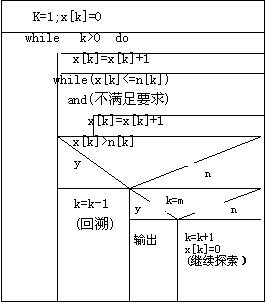
xxxx总结:我们在不断“尝试”之后就可以得到最终的结果,尝试的过程就是不断的枚举式的对每种情况进行检验,找出符合题目要求的结果。
例题一:二叉树中和为某一值的路径
(1)题目描述
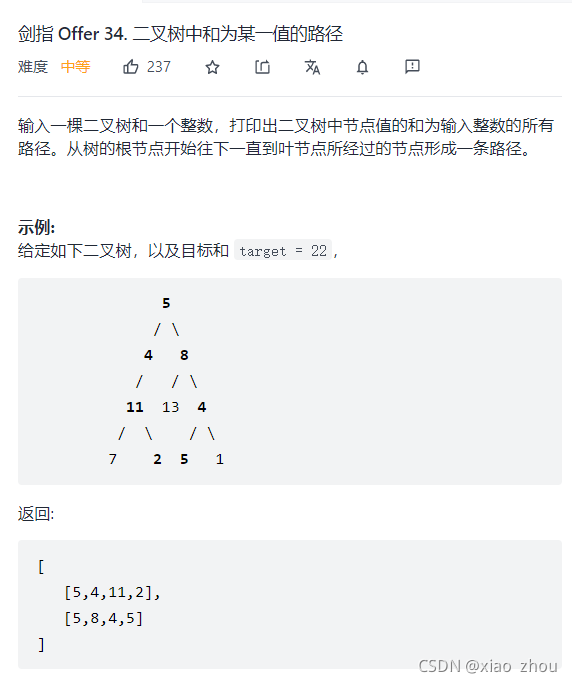
(2)题目分析
xxxx这道题其实比较简单,因为它直接具化成或者本身就是二叉树,所以,我们直接对这个二叉树进行操作即可,并不需要化抽象为具象,把一个事物转化为二叉树。而对于这道题,我们就需要从根节点出发,按照【根,左子树,右子树】这种前序的遍历序列。而前序遍历,我们在处理根的时候,处理的内容就是到这个节点时,路径值之和。只有当节点是叶子节点,并且路径值之和等于目标值即是答案之一。

(3)代码实现
class Solution {
//递归子函数
//参数ret,因为ret要实时变化,所以我们要传引用
//参数ans,因为,每次到达一个结点,都要将值push进ans,但是到叶子结点才能判断是否正确,当我们回溯时,前一个的路径不是下一个路径,递归回去时,值不应该改变,因此要传值
//参数sum,到达某一结点后路径值和,也同ans一样道理,不能实时改变
//目标值固定,是否使用引用都可
void pathSumHelper(TreeNode* root, vector<vector<int>>& ret, vector<int> ans, int sum, int& target)
{
//如果访问到空结点,直接返回即可
if(root == nullptr)
return;
//不是空结点,处理该结点(前序遍历)
sum += root->val;//sum+该结点值
ans.push_back(root->val);//把该结点作为路径push到当前路径ans中
//开始判断,如果是叶子结点,并且路径值之和==目标值,就是正确结果,push进ret
if(root->left==nullptr &&root->right==nullptr && sum==target)
{
ret.push_back(ans);
return;
}
//分别处理左右子树
pathSumHelper(root->left,ret,ans,sum,target);
pathSumHelper(root->right,ret,ans,sum,target);
}
public:
//“主函数”
vector<vector<int>> pathSum(TreeNode* root, int target) {
//用于保存最后结果的vector
vector<vector<int>> ret;
//保存每一个路径,会随着递归进行
vector<int> ans;
//递归子函数
//参数:排查的结点,最终返回的vector,每一个路径,路径值之和,目标路径和
pathSumHelper(root,ret,ans,0,target);
return ret;
}
};
例题二:电话号码的字母组合
(1)题目描述
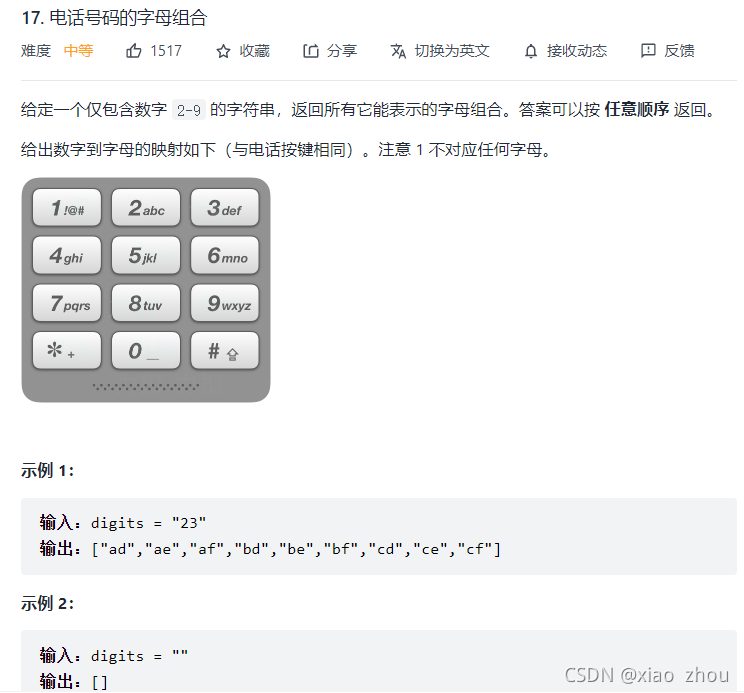
(2)题目分析
xxxx这道题,乍一看可能没有上一道题那么直接就是看出来是树状但是其实想到他是回溯算法也不难。
xxxx这道题就是想得到所有情况,跟一个一个尝试没有区别,只不过它无需判断是否符合条件,只需要将尝试的结果全部接收就好
xxxx对于所有情况,我觉得大家初中时候就学到过“树状图”----用于处理所有可能发生的情况,将所有的情况列出的一种树状结构。这道题就是这种,为了将所有情况列出,就可以采取树状图。下面通过举一个例子,我给大家把树状图实现一下。
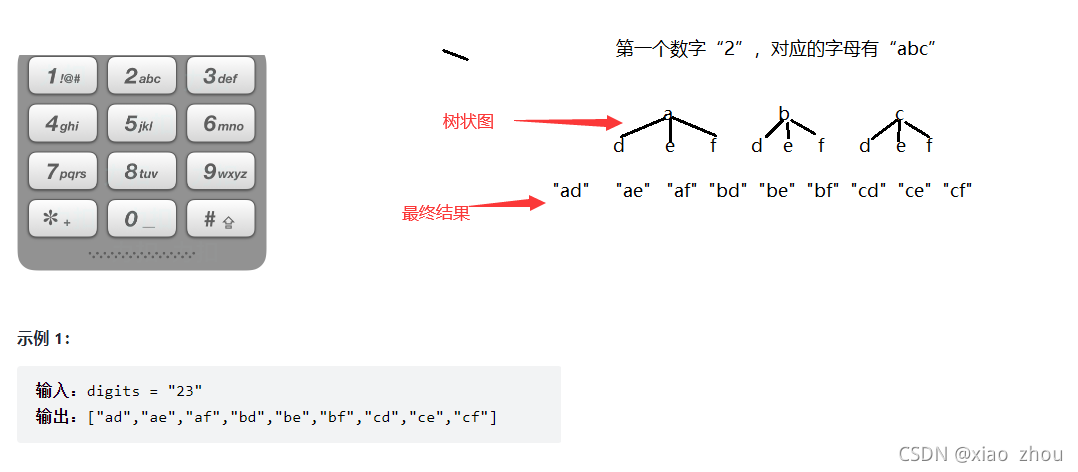
xxxx通过这个树状图我们就可以清楚的明白,这就是一个树状结构,有几个数字,就相当于,这个要递归多少次,按照前序遍历的方式,我们就可以将所有的结果得到。
(3)代码实现
//这是一个小细节,我们定义一个全局的vector<string>,对应数字我们就可以通过这个vector找到对应的所有字母
vector<string> character={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
class Solution {
public:
//递归子函数
void _letterCombinations(const string& digits, vector<string>& ret, int k,string str)
{
//如果k等于了digits的size,说明,所有数字都取完了,一条路径结束。第一次递归结束,是递归的出口,
if(k == digits.size())
{
ret.push_back(str);
return;
}
//取到数字
int num = digits[k]-'0';
//for循环,遍历对应数字的所有字母,每个字母分别对应自己的递归,形成树状结构
for(int i=0;i<character[num].size();i++)
{
//取到该字母
char ch = character[num][i];
//k+1,说明要进行下一个数字,str+ch,将本数字对应的字母添加到str中,保存路径
//继续递归 _letterCombinations(digits,ret,k+1,str+ch);
}
}
//主函数
vector<string> letterCombinations(string digits) {
//也是定义一个用于存储每一个字符串的string
string str;
//存储所有的结果
vector<string> ret;
//如果digits是空的,就直接返回
if(digits.empty())
return ret;
//参数:digits存储数字的字符串
//ret存储最终的结果
//0,digits的其实位置为0
//str,存每一条路径,最后将每一条完整的路径push进ret
_letterCombinations(digits,ret,0,str);
return ret;
}
};