---

typora-copy-images-to: upload

---

前言

此篇文章介绍的排序主要有3个,冒泡排序,选择排序,插入排序,他们有一个共同的特点,那就是时间复杂度都为O(n²).

---

冒泡排序

冒牌排序的思想是,先遍历数组一次,在遍历过程中,通过两两交换的方式把较大的数据放到后面(保证了每次遍历时都能把最大的数放在后面),然后又从头到尾重复此过程,直到有序.如下图(绿色代表在遍历过程中两两比较,橙色代表已经部分排好序):

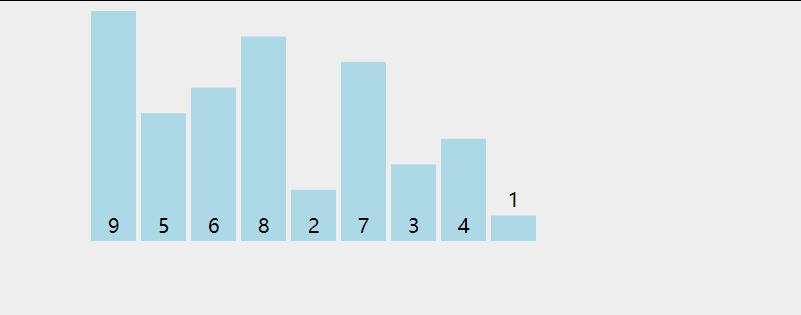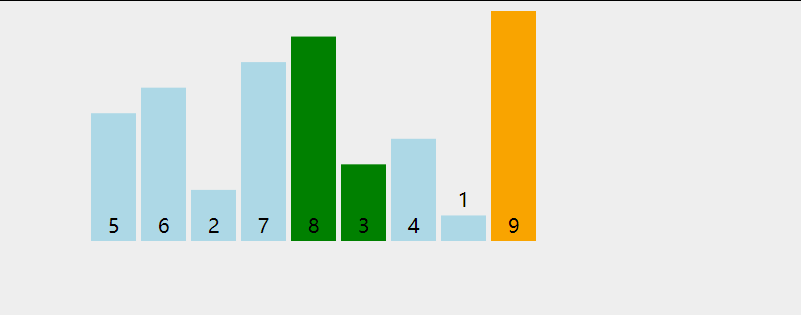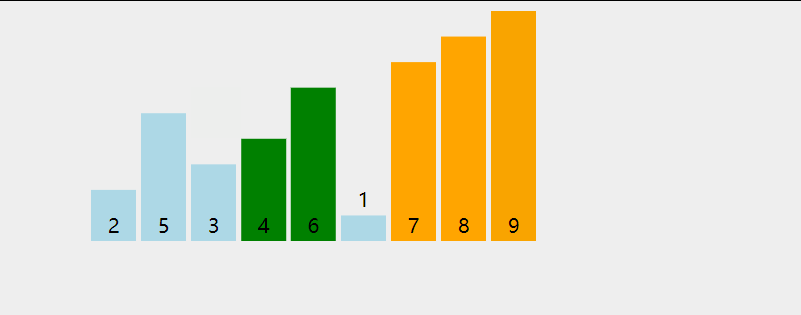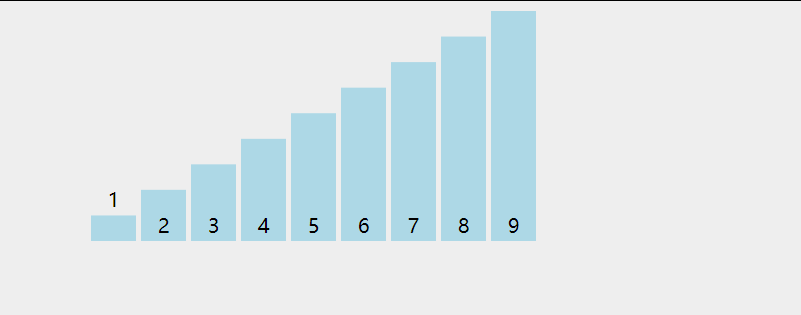
知道了思想,怎么写代码呢,我们先从最简单的一步开始,即只遍历一次,该怎么写,先看看需求:

• 两两交换,说明需要一个交换函数.
• 什么时候需要交换呢?当前者大于后者的时候,也就是说我们需要比较.

所以如果只遍历一次,代码如下:

void swap(int* a,int* b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}
//n是数组长度
for(int j = 0;j<n-1;j++) //小于n-1是因为索引最大为n-1,j代表当前索引,那么j最大只能为n-2
{
    if(num[j] > num[j+1]) //如果前者大于后者就交换,否则继续遍历.
    {
        swap(&num[j],&num[j+1]);
    }
}

现在我们结合遍历一次的代码和上面的动图仔细想想,既然遍历一次就调整好一个最大的数字在最后面,那么我们要遍历多少次才能把全部的数字排好序呢?没错,答案是n-1次,因为有n个数字,但是是通过两两比较实现的,**当索引[1,n-1]**都有序后,索引为0的数字一定比索引为1的数字小,就不需要再比较了.

所以冒泡排序的代码如下:

void BubbleSort(int num[],int n)
{
    for(int i = 0;i<n-1;i++) //需要遍历n-1次
    {
        //n是数组长度
        for(int j = 0;j< n-1 - i;j++) //小于n-1-i是因为每一次完整遍历数组后,最后一个数字一定是最大的,下一次遍历就不需要再管它.
        {
            if(num[j] > num[j+1]) //如果前者大于后者就交换,否则继续遍历.
            {
                swap(&num[j],&num[j+1]);
            }
        }
    }
}

测试:

---

选择排序

选择排序的思想是,先假设未排序第一元素是最小的,然后遍历一遍数组看是否有比假想的最小数更小的数,如果有就记录索引,遍历完成以后把真正的最小数与最初的假想最小数交换.然后继续重复上面过程.如下图(绿色代表正在遍历,红色代表定位最小数,橙色代表部分排好序):

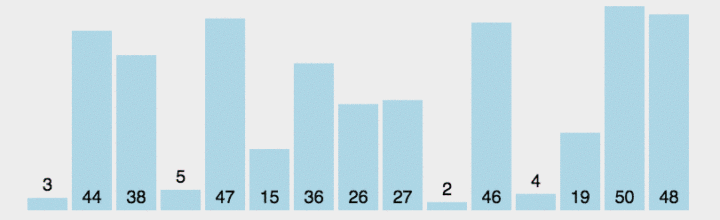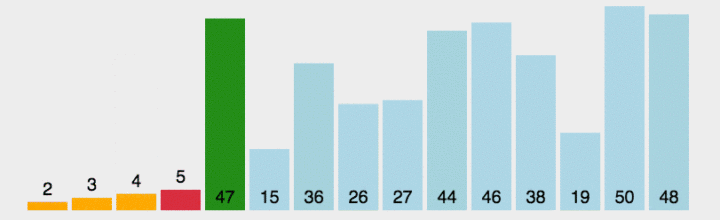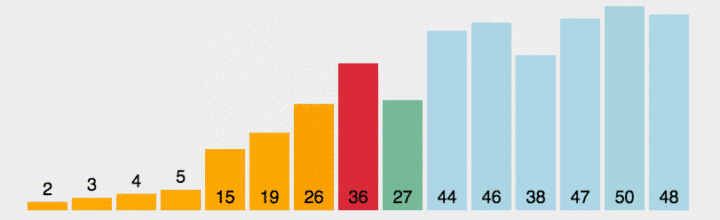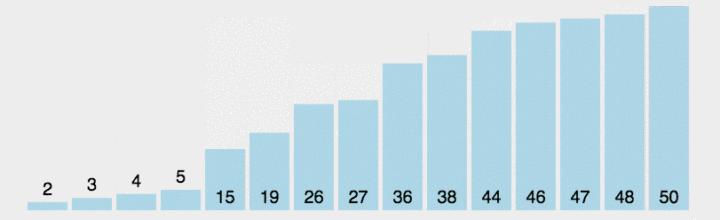
同样道理,我们由简到繁,先写出只遍历一次时候的代码,那么只遍历一次时候需要的准备是:

• 用于记录最小元素的索引变量min_index.
• 交换函数.

代码如下:

//n是数组长度
int min_index  = 0; //0代表未排序元素的头的索引.
for(int j = 0 + 1;j<n;j++) //j从头的下一个位置开始
{
	if(num[j] < num[min_index])  //如果当前元素比最小元素小
    {
        min_index = j;    //就记录最下元素的索引
    }
}
swap(&num[0],&num[min_index]);  //最小元素与头进行交换.

这个和冒泡排序是不是几乎一样?遍历一次便能够确定一个最小的数,然后放到首位,那么需要多少次呢?答案是n-1次

所以完整的代码如下:

void SelectSort(int num[],int n)
{
    for(int i = 0;i<n-1;i++) //需要遍历n-1次
    {
        int min_index  = i; //i代表   未排序元素   的头的索引.
        for(int j = i + 1;j<n;j++) //j从头的下一个位置开始
        {
            if(num[j] < num[min_index])  //如果当前元素比最小元素小
            {
                min_index = j;    //就记录最下元素的索引
            }
        }
        swap(&num[i],&num[min_index]);  //最小元素与头进行交换.
    }
}

测试:

---

插入排序

插入排序的思想是,从索引j(范围为1到n-1)开始,保证[0,i]区间的元素有序,怎么保证呢? 先把索引为i的元素保存下来(变量target),然后依次往前比较,如果前面的元素比target大,就往后放,否则停止.如图(橙色代表部分有序,绿色代表从i开始往前遍历,红色代表原索引i元素):

仍然一样的思想,先从简到繁,如若只执行一次,该怎样操作?

int target = num[i];  //索引为[0,i]区间中索引为i的元素
int aim = i;          //aim是用于记录target真正应该的位置
for(int j = i;j>0;j--)  
{
    if(num[j-1] > target) num[j] = num[j-1],aim = j-1;//如果前面大于target,前面就覆盖后面,并且aim更新位置.
}
num[aim] = target; //target回到自己应该的位置.

现在我们看向上图,可以发现,i是从1开始递增的.所以完整代码为:

void InsertSort(int num[],int n)
{   
    for(int i =1;i<n;i++)
    {
        int target = num[i];  //索引为[0,i]区间中索引为i的元素
        int aim = i;          //aim是用于记录target真正应该的位置
        for(int j = i;j>0;j--)  
        {
            if(num[j-1] > target) num[j] = num[j-1],aim = j-1;//如果前面大于target,前面就覆盖后面,并且aim更新位置.
        }
        num[aim] = target; //target回到自己应该的位置.
    }
}

测试

---

冒泡排序优化

大家有没有想过,对于冒泡排序,如果数据本来就是有序的,是没必要再比下去的,但是冒泡排序却不得不仍然要比n*(n-1)/2次,所以我们给其加个flag,第一遍遍历时判断是否有序,如果有序,就结束.

void BubbleSort(int num[],int n)
{
    for(int i = 0;i<n-1;i++) //需要遍历n-1次
    {
        int flag =  1; //等于1代表假设是有的
        for(int j = 0;j< n-1 - i;j++)
        {
            if(num[j] > num[j+1]) 
            {
                swap(&num[j],&num[j+1]);
                flag = 0; //如果交换了数字,说明无效,变为0;
            }
        }
        if(flag) break;//如果有序就停止
    }
}

---

选择排序优化

受到上面冒泡排序的启示,大家可能会想,如果有序就怎么样…但是这种形式的优化对于选择排序来说是没有意义的,因为根本无法达到.

那么优化选择排序是优化的哪些呢?

选择的思路是把最小的放到最前面,那么我们可不可以在遍历一次的时候同时找到最大和最小呢?然后最小放前面,最大放后面呢?

void SelectSort(int num[],int n)
{
    for(int i = 0;i<n-1;i++)
    {
        int min_index = i; //假设索引为i元素最小
        int max_index = i; //假设索引为i元素最大
        for(int j = i + 1;j < n-i;j++)  //j小于n-i是因为最后面的元素在逐渐有序,便不需要再管
        {
            if(num[j] < num[min_index]) 
            {
                min_index = j;    //更新最小
            }
            if(num[j] > num[max_index])
            {
                max_index = j;    //更新最大
            }
        }
        
        swap(&num[i],&num[min_index]); //把最小的放前面
        
        if(max_index == i) max_index = min_index; //如果最大值在头,那么最小值放在前面后,最大值就被换到min_index位置
        
        swap(&num[n-1-i],&num[max_index]);//最大的放后面
        
    }
}

---

插入排序优化

大家想想,插入排序可以怎么优化呢?其实插入排序由于自身的特性,几乎优化不了,比如数据有序,插入排序遍历一遍就知道了,那我们说的插入排序优化是什么呢?这个博主会放到另一篇文章讲,因为插入的改进后就是另一个排序,希尔排序