本文目录
- 针对词语
- 针对句子
- 针对文章
针对词语
关键词提取
TF-IDF
TF-IDF是一种统计方法,用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成反比下降。TF-IDF加权的各种形式常被搜索引擎应用,作为文件与用户查询之间相关程度的度量或评级。除了TF-IDF以外,因特网上的搜索引擎还会使用基于链接分析的评级方法,以确定文件在搜寻结果中出现的顺序。
词频(Term Frequency ): 𝑡𝑓𝑡,𝑑 =𝑐𝑜𝑢𝑛𝑡(𝑡, 𝑑)
逆文档频率(Inverse Document Frequency): 𝑖𝑑𝑓𝑡 = log10(𝑁/𝑑𝑓𝑡)
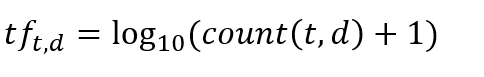

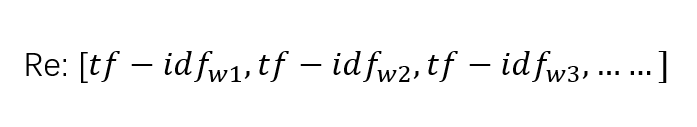
Text-Rank
先介绍下PageRank。
谷歌的两位创始人的佩奇和布林,借鉴了学术界评判学术论文重要性的通用方法,“那就是看论文的引用次数”。由此想到网页的重要性也可以根据这种方法来评价。于是PageRank的核心思想就诞生了:
如果一个网页被很多其他网页链接到的话说明这个网页比较重要,也就是PageRank值会相对较高
如果一个PageRank值很高的网页链接到一个其他的网页,那么被链接到的网页的PageRank值会相应地因此而提高
Text-Rank
- 如果一个单词出现在很多单词后面的话,那么说明这个单词比较重要
- 一个TextRank值很高的单词后面跟着的一个单词,那么这个单词的TextRank值会相应地因此而提高


针对句子
分句-NLTP工具
- 输入:句子或者句子序列的混合物
- 输出:单个句子的序列
分词-结巴分词
使用案例
import sys
sys.path.append("../")
import jieba
import jieba.posseg
import jieba.analyse
print('='*40)
print('1. 分词')
print('-'*40)
seg_list = jieba.cut("我来到我理想的大学", cut_all=True)
print("Full Mode: " + "/ ".join(seg_list)) # 全模式
seg_list = jieba.cut("我来到我理想的大学", cut_all=False)
print("Default Mode: " + "/ ".join(seg_list)) # 默认模式
seg_list = jieba.cut("他来到了腾讯大厦")
print(", ".join(seg_list))
seg_list = jieba.cut_for_search("A硕士毕业于哈佛大学,后在东京大学深造") # 搜索引擎模式
print(", ".join(seg_list))
print('='*40)
print('2. 添加自定义词典/调整词典')
print('-'*40)
print('/'.join(jieba.cut('如果放到post中将出错。', HMM=False)))
#如果/放到/post/中将/出错/。
print(jieba.suggest_freq(('中', '将'), True))
#494
print('/'.join(jieba.cut('如果放到post中将出错。', HMM=False)))
#如果/放到/post/中/将/出错/。
print('/'.join(jieba.cut('「台中」正确应该不会被切开', HMM=False)))
#「/台/中/」/正确/应该/不会/被/切开
print(jieba.suggest_freq('台中', True))
#69
print('/'.join(jieba.cut('「台中」正确应该不会被切开', HMM=False)))
#「/台中/」/正确/应该/不会/被/切开
print('='*40)
print('3. 关键词提取')
print('-'*40)
print(' TF-IDF')
print('-'*40)
s = "从实时画面看,京藏高速北京清河收费站双向顺畅,京沪高速上海江桥收费站通行缓慢,车辆已经排起长龙,绵延数公里。"
for x, w in jieba.analyse.extract_tags(s, withWeight=True):
print('%s %s' % (x, w))
print('-'*40)
print(' TextRank')
print('-'*40)
for x, w in jieba.analyse.textrank(s, withWeight=True):
print('%s %s' % (x, w))
print('='*40)
print('4. 词性标注')
print('-'*40)
words = jieba.posseg.cut("我是中国人,我爱中国")
for word, flag in words:
print('%s %s' % (word, flag))
print('='*40)
print('6. Tokenize: 返回词语在原文的起止位置')
print('-'*40)
print(' 默认模式')
print('-'*40)
result = jieba.tokenize('江南造船厂')
for tk in result:
print("word %s\t\t start: %d \t\t end:%d" % (tk[0],tk[1],tk[2]))
print('-'*40)
print(' 搜索模式')
print('-'*40)
result = jieba.tokenize('江南造船厂', mode='search')
for tk in result:
print("word %s\t\t start: %d \t\t end:%d" % (tk[0],tk[1],tk[2]))


命名实体识别
详见
词性标注
词性标注(Part-Of-Speech tagging, POS tagging)也被称为语法标注(grammatical tagging)或词类消疑(word-category disambiguation),是语料库语言学(corpus linguistics)中将语料库内单词的词性按其含义和上下文内容进行标记的文本数据处理技术 [1-2] 。
词性标注可以由人工或特定算法完成,使用机器学习(machine learning)方法实现词性标注是自然语言处理(Natural Language Processing, NLP)的研究内容。常见的词性标注算法包括隐马尔可夫模型(Hidden Markov Model, HMM)、条件随机场(Conditional random fields, CRFs)等 [2-3] 。
词性标注主要被应用于文本挖掘(text mining)和NLP领域,是各类基于文本的机器学习任务,例如语义分析(semantic analysis)和指代消解(coreference resolution)的预处理步骤。
依存分析
基于依存文法的句法分析。分析结果为句子中词语间依存关系组成的依存树。
序列标注
序列标注是NLP中一个重要的任务,它包括分词、词性标注、命名实体识别等等,一般使用以下方法解决:
- HMM 隐马尔可夫模型
- CRF 条件随机场
- BiLSTM+CRF
- Lattice+LSTM+CRF
- BERT+CRF
针对文章
PLSA
PLSA是一个词袋模型(BOW, Bag Of Word),它不考虑词在文档中出现的顺序,但可以把词在文档中的权重考虑进来。
SVD奇异值分解
对矩阵分解从而得到特征
对于奇异值,它跟我们特征分解中的特征值类似,在奇异值矩阵中也是按照从大到小排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。
LDA
线性判别式分析(Linear Discriminant Analysis),简称为LDA。也称为Fisher线性判别(Fisher Linear Discriminant,FLD),是模式识别的经典算法,在1996年由Belhumeur引入模式识别和人工智能领域。
基本思想是将高维的模式样本投影到最佳鉴别矢量空间,以达到抽取分类信息和压缩特征空间维数的效果,投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离,即模式在该空间中有最佳的可分离性。
LDA与前面介绍过的PCA都是常用的降维技术。PCA主要是从特征的协方差角度,去找到比较好的投影方式。LDA更多的是考虑了标注,即希望投影后不同类别之间数据点的距离更大,同一类别的数据点更紧凑。
EM算法
最大期望算法(Expectation-Maximization algorithm, EM),或Dempster-Laird-Rubin算法 [1] ,是一类通过迭代进行极大似然估计(Maximum Likelihood Estimation, MLE)的优化算法 [2] ,通常作为牛顿迭代法(Newton-Raphson method)的替代用于对包含隐变量(latent variable)或缺失数据(incomplete-data)的概率模型进行参数估计 [2-3] 。
EM算法的标准计算框架由E步(Expectation-step)和M步(Maximization step)交替组成,算法的收敛性可以确保迭代至少逼近局部极大值 [4] 。EM算法是MM算法(Minorize-Maximization algorithm)的特例之一,有多个改进版本,包括使用了贝叶斯推断的EM算法、EM梯度算法、广义EM算法等 [2] 。
由于迭代规则容易实现并可以灵活考虑隐变量 [3] ,EM算法被广泛应用于处理数据的缺测值 [1-2] ,以及很多机器学习(machine learning)算法,包括高斯混合模型(Gaussian Mixture Model, GMM) [5] 和隐马尔可夫模型(Hidden Markov Model, HMM) [6] 的参数估计。