缘起
最近项目中用到了终端在仅有电流的情况下启动并正常工作的需要。此时需要先给系统充电,充电时间是毫秒级别。而 MCU 在 2V 基本就可以工作了,此时的 ADC 的基准电压也在 2V(使用的基准电压芯片只能保证在 2.5V ~ 3.3V 内是准确的),这就造成了 ADC 在这段时间内工作采样数据不准确。问题就是想搞明白此时基准电压低了,采样值会如何变化?
知其然,也要知其所以然!
国内基本找不到太有效的讲解 ADC 原理的资料(至少我是没找到),在 TI、ADI 等公司官网倒是有不少资料可供参考!
基本原理
STM32 微控制器中内置的 ADC 使用 SAR(Successive Approximation Register,逐次逼近)原则,分多步执行转换。SAR ADC 的工作原理基本都是一样的。下图左侧是 ST 给出的 ADC(以 10 位为例) 的基本原理图,右侧是专用 16 位高精度 SAR ADC 基本原理图:
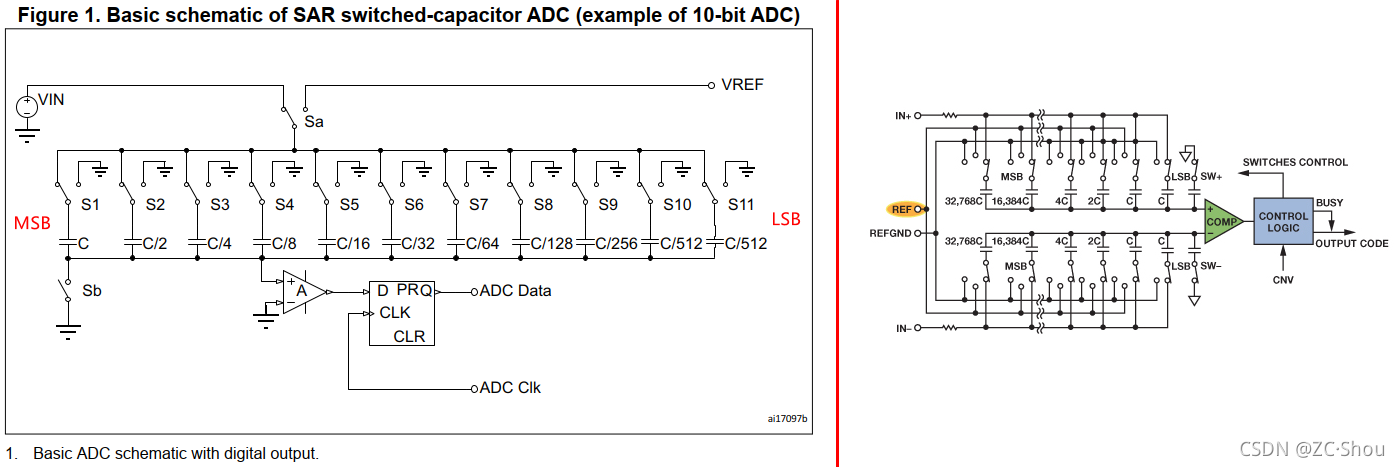
- VIN / IN+:很多专用 ADC 手册都是都是标注为 VIN,这个就是 ADC 的输入引脚
- VREF / REF:这个就是 ADC 的参考电压,部分手册标注为 Vref
- REFGND 和 IN- 在 ST MCU 的实际使用中,多数都是直接接系统地的。因此,左侧图中,地都是一样的。
- 注意以上电容容量一共是 2C:
C / 2 + C / 4 + C / 8 + C / 16 + C / 32 + C / 64 + C / 128 + C / 256 + C / 512 + C / 512 = C,C + C = 2C,这在下面转换时需要用到。
LSB:Least Significant Bit,最低有效位
MSB:Most Significant Bit,最高有效位
ADC 输入电压的最小可检测增量变化用 LSB 表示,1LSB = VREF / 2n,n 表示 ADC 的有效位数。例如,上图 10 位 ADC,VREF 为 3.3V 时:1LSB = 3.3 / 210 = 0.0032226V = 3.222mV = 322.2uV
转换步骤
SAR ADC 的转换步骤数等于 ADC 转换器中的位数,每个 ADC 时钟产生一个数据位。转换步骤可以大体上划分为 采样 -> 保持 -> 逐次转换 这三步。下面我们来具体看看这三步是怎么来执行的。
- 采样状态: 开关 Sa 切换至 VIN,采样期间开关 Sb 闭合,电容充电至电压 VIN。
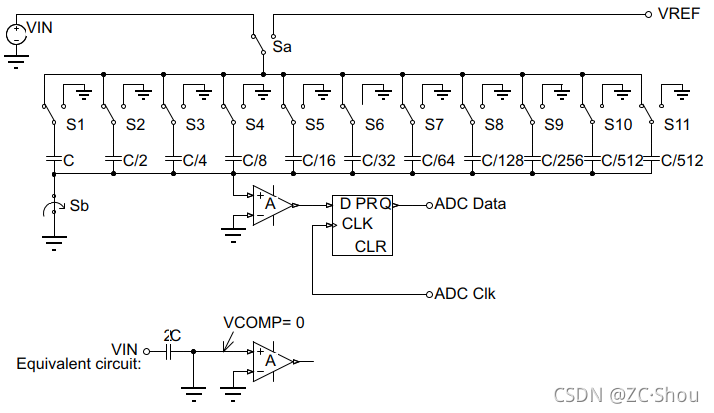
- 保持状态: 开关 Sb 打开,然后开关 S1 ~ S11 切换至接地且 Sa 切换至 VREF,输入断开,电容保持输入电压。保持状态仅仅是个临时态,实际在这个阶段就开始进行转换。
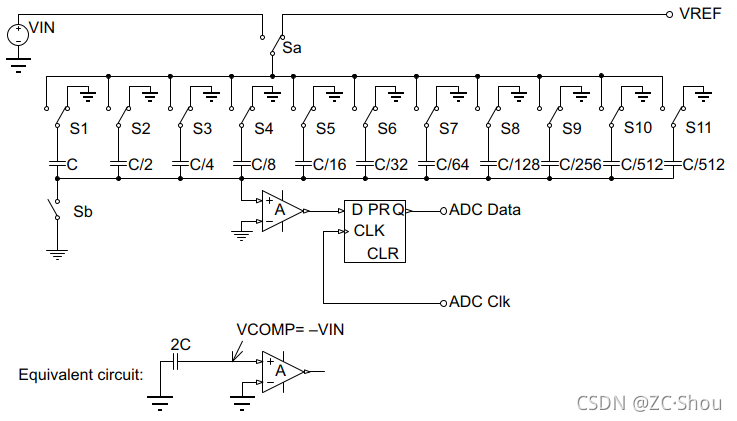
- 转换: 每个 ADCCLK 执行一步,每一步 ADC 输出一位数。首先来看下图:
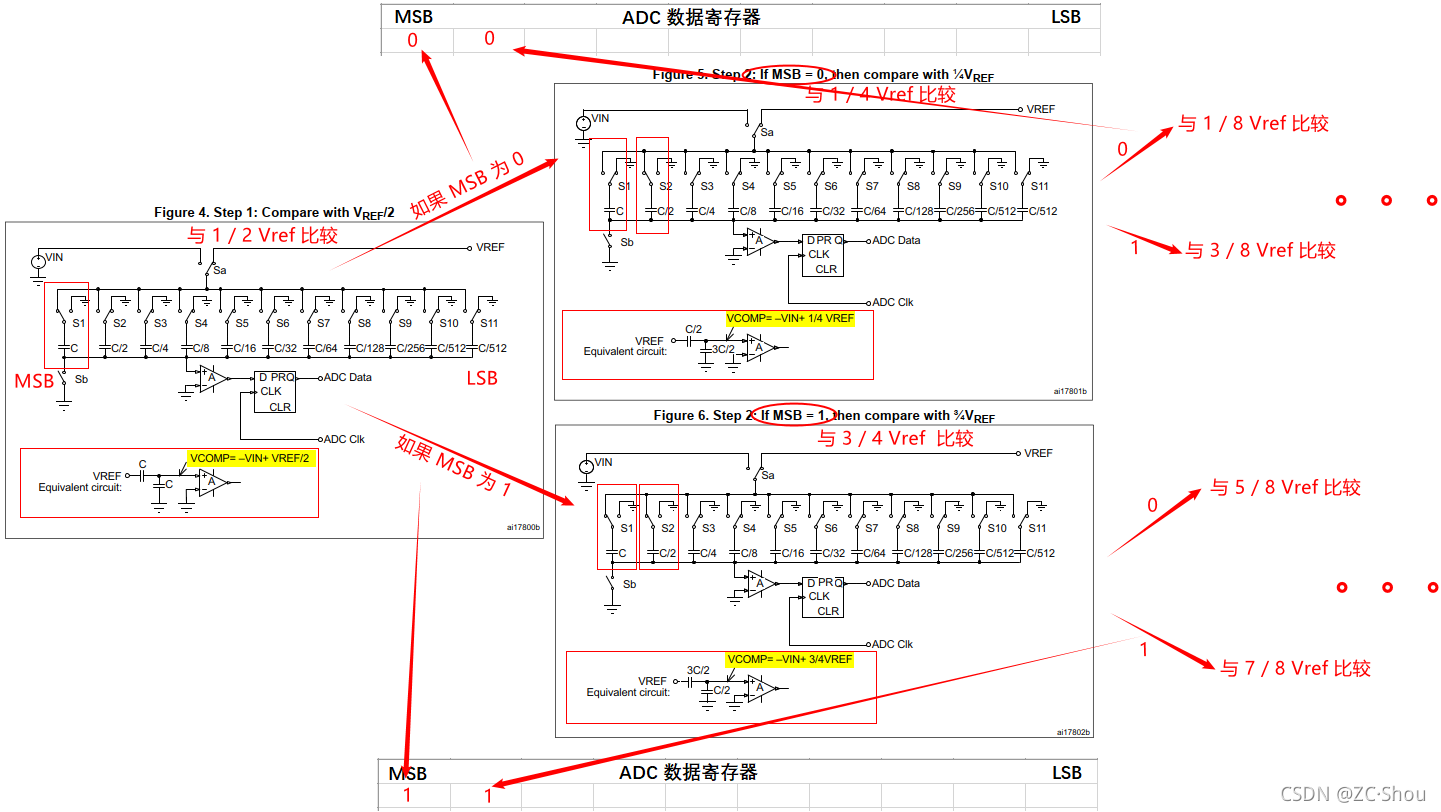
其实,看上面的电容值就可以看出来,对比过程就是简单的二分法进行逐次逼近到 ADC 指定的精度(位数),就是个二叉树。如下图所示的分解图:
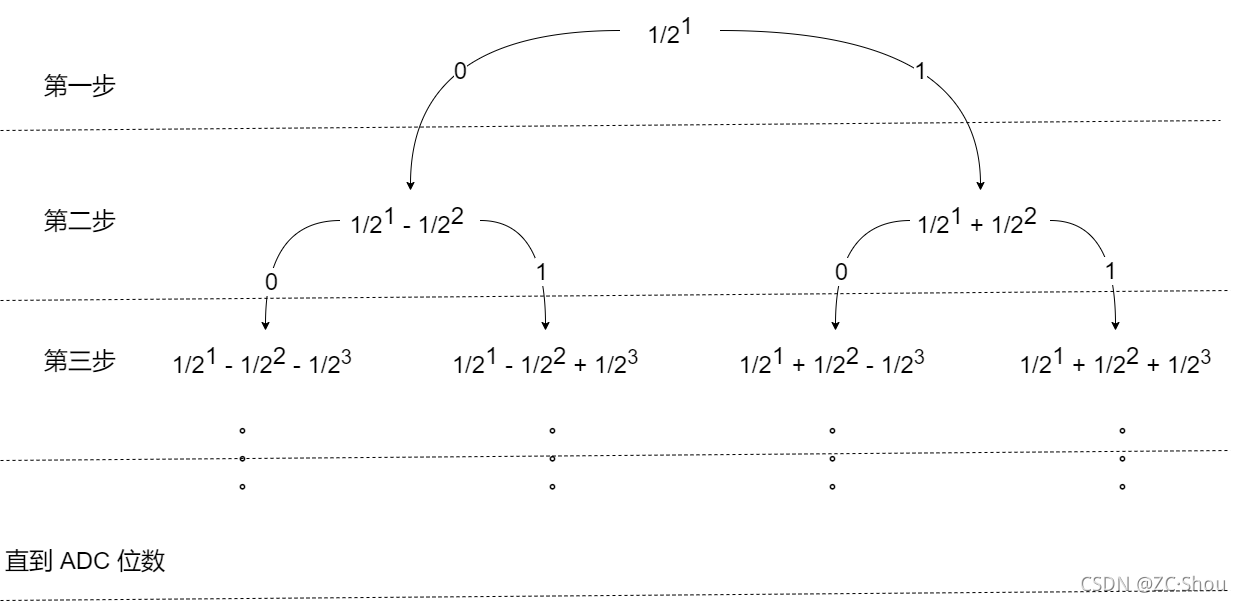
有了以上原理之后,很容易得出 ,对于一个有 10 位有效位的 ADC 来说,其可能步骤有 210 = 1024 个可能的步骤,ADC 转换的数值 = (VIN x 1024) / VREF。通用公式:ADCsrc = VIN * 2n / Vref,n 为 ADC 的有效位数 。
转换时间
搞明白了以上工作原理之后,我们再来看看 ST 手册中给出的 ADC 采样时间公式:每个通道总的转换时间 = TSampling + Tconversion
- TSampling :这个是我们在配置 ADC 时指定的。该值需要和外部电路的输入阻抗匹配。这一步就是保证在采用阶段,采样保持电容有足够的时间充电。
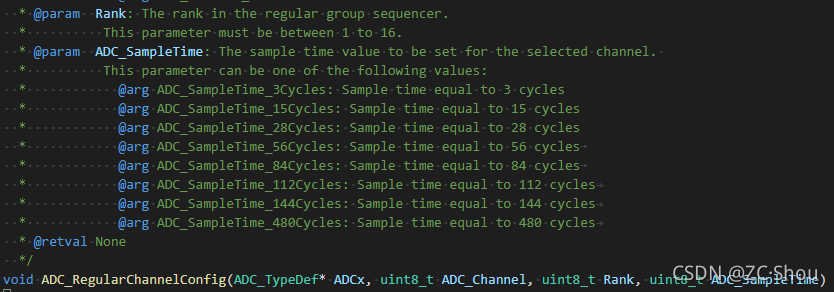
- Tconversion :取决于转换精度,这个也是在配置 ADC 时指定的。具体取值如下:
精度 TConversion 12 bits 12 * ADCCLK 10 bits 10 * ADCCLK 8 bits 8 * ADCCLK 6 bits 6 * ADCCLK
因此,每个通道总的转换时间就是:Ttotal = (SMP + RES) * ADCCLK。其中,SMP 是采样时间,需要和外部输入阻抗搭配;RES 是转换精度,降低精度可提高速度;ADCCLK 是 ADC 模块工作时钟
外部输入阻抗和采样时间
上面我们说道,TSampling 需要和外部输入阻抗相匹配。那么,这个外部输入阻抗具体怎么来计算,或者说如何进行确定呢?首先,来看一下 ST 给出的下图:
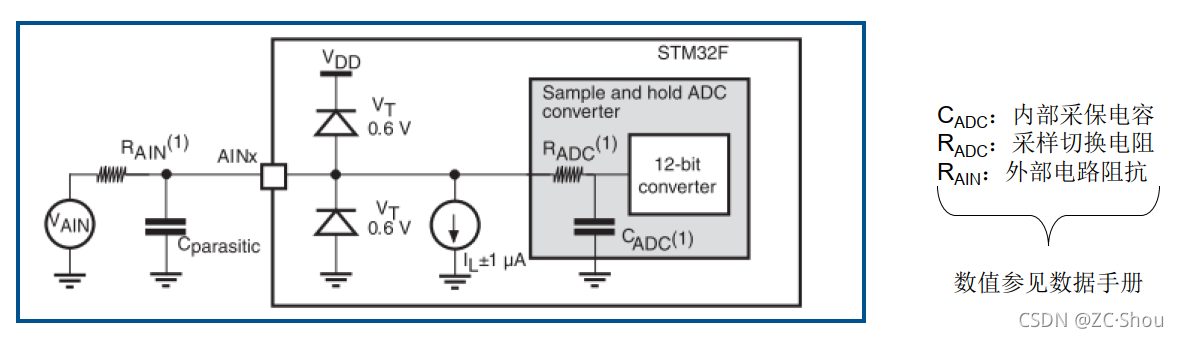
不同 ADC 配置下允许的最大外部输入阻抗计算公式如下 :
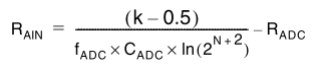
- K:采样周期
- N:转换精度
- fADC:取决于工作电压
- CADC 和 RADC:这个是设计 ADC 的固有参数,位置见上图,具体数值参考数据手册
举个例子,在 30MHz 的 ADC 时钟;12 位转换精度;3 个周期采样的配置下,允许的最大外部输入阻抗 RAIN = [ ( 3 - 0.5 ) / ( 30M * 4 * 14 * ln2 ) ] – 1.5KΩ = 0.65KΩ。注意,这里的 CADC 和 RADC 的值取自于 STM32Fx 的数据手册。
参考电压
为 VREF 提供电压的源的稳定性是影响 ADC 精度的一个重要因素。电源或电压调节器的输出可能会因温度或负载波动等原因而变化。下图表示了 ADC 的参考电压在不同值时导致输出变化的关系。
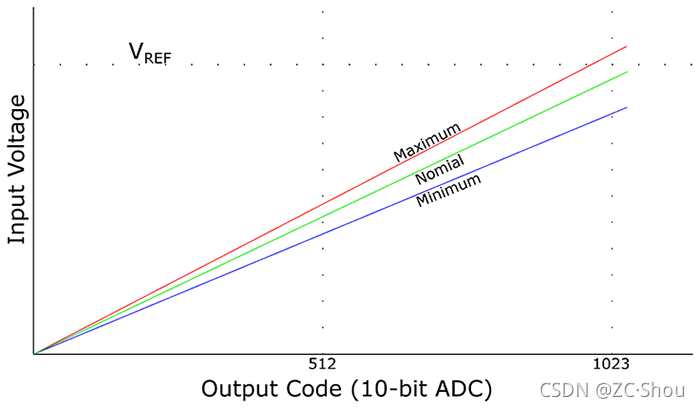
当 ADC 输入电压超出基准电压,哪怕只有很短的一段时间,它也会向基准电压源注入电流,因此基准电压源必须要能吸取一定量的电流。基准电压源可集成具有足够驱动电流的缓冲器,也可采用适当的运算放大器作为缓冲器。下图是一个典型的精密逐次逼近型 ADC 基准电压源电路:
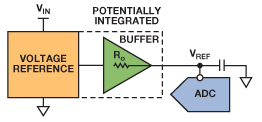
ADC 基准电压输入端的开关电容具有动态负载,因此基准电压源电路必须能够处理与时间和吞吐速率相关的电流。为避免转换误差,特定吞吐速率下所需的平均电流不应使基准电压下降超过 ½ LSB。
ADC 误差
前面说了,基准电压会影响 ADC 的精度,在使用了合适的基准电压芯片之后,参考电压的误差我们暂且不考虑,ADC 本身也会有很多原因造成误差。非理想 ADC 的直流误差主要是偏置电压误差和增益误差。下图是一个三位 ADC 带有偏移和增益误差的理想和实际ADC 转换对比图。
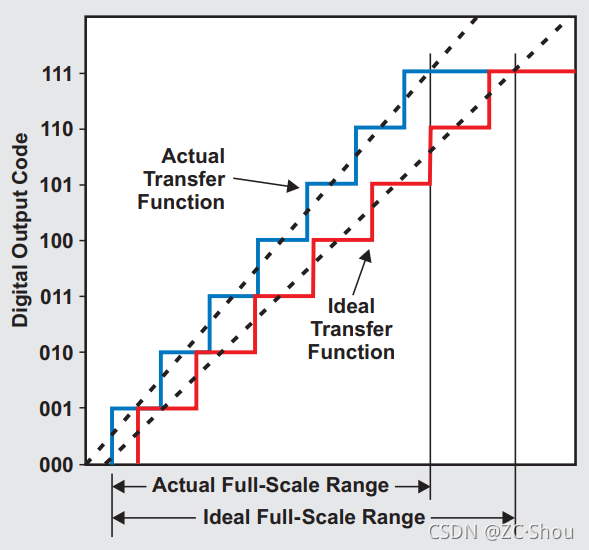
偏移误差是第一次实际转换和第一次理想转换之间的偏移造成的误差。第一次转换发生在数字 ADC 输出从 0 变为 1 时。引入了偏移误差之后,原来 ADC 采样值的公式就可以表示为:ADCsrc = (VIN - Voffsef) * 2n / Vref,n 为 ADC 的有效位数
增益误差等于从零到满刻度的理想斜率与从零到满刻度的实际斜率之间的差。再引入了增益误差之后,原来 ADC 采样值的公式就可以表示为:ADCsrc = (VIN - Voffsef) * 2n / ( Vref ( 1 - GEADC)),n 为 ADC 的有效位数,GEADC = (实际增益 - 理想增益) / 实际增益
除了以上两个误差之外,ST 还列举了以下一些误差:
- 微分线性误差:微分线性误差(DLE)为实际步进和理想步进之间的最大偏离。
- 积分线性误差:积分线性误差为任何实际转换和端点相关线间的最大偏离。
- 总未调整误差:总未调整误差(TUE)为实际和理想传输曲线间的最大偏离。
关于每个误差的解释以及对应的处理,ST 给出的手册中有很详细的说明,这里就不多说,具体参见 《AN2834 Application note How to get the best ADC accuracy in STM32 microcontrollers》
参考
- https://www.analog.com/cn/analog-dialogue/articles/precision-successive-approximation-adcs.html
- https://www.st.com/resource/en/application_note/cd00211314-how-to-get-the-best-adc-accuracy-in-stm32-microcontrollers-stmicroelectronics.pdf
- http://news.eeworld.com.cn/mcu/article_2017021933866.html
- https://www.ti.com/lit/an/slyt331/slyt331.pdf?ts=1631704840654&ref_url=https%253A%252F%252Fwww.google.com%252F