文章目录
- 方法概述
- 什么是方法?
- 方法的结构
- 方法使用
- 方法定义和调用
- 方法调用注意
- 方法三种调用格式
- 方法重载
- 方法重载前
- 方法重载后
- 重载练习
- 练习1
- 练习2
- 方法递归
- 递归常见应用
- 求n的阶乘
- 第n个斐波那契数
- 青蛙跳台阶问题
- 汉诺塔问题
- 迷宫回溯问题
- 八皇后问题
- 代码块
- 代码块的作用
- 代码块分类
- 静态代码块
- 非静态代码块
- 类中对属性可以赋值的位置
方法概述
什么是方法?
方法是将一组完成特定功能的代码整合在一起,以达到简化开发,减少代码耦合,提高代码复用性的结构,类似与C语言中的函数。
简化开发:将完成特定功能的代码封装在方法内,当我们在调用所需要的方法时,无须关心方法内部的具体实现,只需要知道哪些方法可以完成我们的功能,可以使得开发人员更加专注于自己所要去实现的功能。
减少代码耦合:好的程序设计是高内聚、低耦合的,将具有特定功能得代码封装在方法内,可以使得程序结构变得更加清晰,代码的可读性也更加好,降低了开发的复杂度。
提高代码复用性:方法可以减少冗余的代码,当我们在编写程序时,出现了大量冗余代码时,应该考虑使用方法将其封装在内,这样每当我们需要使用相应功能时只需要调用相应的方法即可。实现了一个方法的多处使用。
方法的结构
[权限修饰符] [关键字] 返回值类型 方法名([参数列表]) [throws 异常类型] {
方法体
}
- 权限修饰符,对应了4种权限,public、protected、缺省(包权限)、private。【封装内容】
- 关键字,修饰方法的关键字常用的有:static(静态)、abstract(抽象)、final(断子绝孙)、synchronized(同步)…
- 返回值类型,可以是基本数据类型和引用类型
- 方法名,见名知意,小驼峰命名
- 参数列表,方法所需要的参数,包括数据类型和参数名。【注意】java中采用的值传递机制,基本数据类型传递的是变量的值,引用数据类型传递的是引用变量的hash地址值
- throws 异常类型,声明方法可能抛出的异常,异常是程序执行中发生的不正常情况,异常在Java中也是类,所有异常的最高父类是Throwable,其下有两个子类Error和Exception。
- 方法体,方法功能的具体实现。
// 例如: main方法
public static void main(String[] args) {
//...
}
tips:
- static修饰的方法属于静态方法,静态方法中不能调用非静态的方法和属性
原因:
静态方法属于类不属于对象(面向对象,目前了解),在类中,静态的结构(static修饰的)随着类的加载而加载,而非静态结构属于类的对象,只有在对象被创建后,才会在堆空间中创建,所以非静态结构是晚于静态结构加载的。因此,静态方法中不能调用非静态的方法和属性。
方法使用
方法定义和调用
- 方法定义的先后顺序无所谓。
- 方法定义在当中,方法不能嵌套定义。
- 方法定义关系平等,不能嵌套。
- 使用方法需要调用方法。
// 原来写在main函数中的代码, 可以写在方法中
public class Demo01Method {
public static void main(String[] args) {
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 20; j++) {
System.out.print('*'); // 不换行
}
System.out.println(); // 只换行不输出
}
}
}
将上诉代码封装在方法中实现
public class Demo01Method {
public static void main(String[] args) {
printMethod(); //方法调用
}
// 方法定义
public static void printMethod(){
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 20; j++) {
System.out.print('*');
}
System.out.println();
}
}
}
方法调用注意
- 方法传参时,实参的数据类型和个数要严格与方法定义中的参数列表匹配
// 方法定义
public void method(int a, double b){
//...
}
public void test(){
method(); // 错误, 没有参数
method(1); // 错误, 参数个数不匹配
method(1.23,1); // 错误, 参数类型不匹配, double无法自动向下转型
method(1,1.23); // 【正确】
}
-
方法只能有一个返回值。使用return关键字来返回值。
return的作用:1)结束当前方法 2)返回方法的返回值。
// 方法定义
public int method(int a, double b){
//...
return 1,2; // 错误
}
public int method(int a, double b){
//...
return 1;
return 2; // 错误, return会结束当前方法, 后面的代码永远执行不到,并且编译也会报错
}
public int method(int a, double b){
//...
return 0;
}
// 需要返回多个值时,可以使用容器(数组,集合)
- return的返回值类型必须严格与定义的返回值类型相同。
public int method(int a, double b){
//...
return 1.0; // 错误返回值类型为int,return企图返回double
}
public int method(int a, double b){
return 0; // 正确
}
- 方法的调用会在栈空间开辟栈帧,方法内部的变量
方法三种调用格式
- 单独调用
method(para1,...); - 打印调用
System.out.println(method(para1,...)); - 赋值调用
dataType var = method(para1,...);
public class Demo02MethodDefine {
// 方法实现求和
public static void main(String[] args){
// 单独调用
getSum(10,20);
// 打印调用
System.out.println(getSum(10,20));
// 赋值调用
int res = getSum(10,20);
System.out.println(res);
}
public static int getSum(int x, int y){
return x + y;
}
}
方法的返回值类型为void,只能单独调用,不能打印或者赋值调用,因为没有返回值。
方法重载
方法重载(overload):指在同一个类中,允许存在一个以上的同名方法,只要它们的参数列表不同即可,与修饰符、参数的名称和返回值类型无关。
参数列表:参数个数不同,数据类型不同,多类型的顺序不同。
重载方法调用:JVM通过方法的参数列表,调用不同的方法。
说明:对于继承关系中的“重载”,个人认为子类继承了父类的方法,也就是子类结构中隐式存在继承的方法,对于这个方法的重载应该也是发生在本类中的,个人观点。
方法重载前
在没有方法重载之前,如果要需要对不同的数据进行功能大体相同的操作,需要定义多个不同名的方法。
例如:需要完成加法功能的方法,但是方法的参数可能是两个整型,两个浮点型或者是三个整型,四个浮点型… 那么就需要编写多个不同名的方法进行调用,但是这些方法所实现的核心功能都是进行加法计算,当参数列表变化很多时,方法的名字也就越来越多,对于实际开发非常不友好。
public class Demo01Method {
public static void main(String[] args){
// 这样调用方法非常复杂,需要记住对应方法的名字。
System.out.println(sumInt1(10, 20));
System.out.println(sumInt2(10, 20, 30));
System.out.println(sumDouble1(11.1, 22.2));
System.out.println(sumDouble2(11.1, 22.2, 33.3, 44.4));
}
// 参数不同,但是功能大致相同的方法
public static int sumInt1(int a, int b){
return a + b;
}
public static int sumInt2(int a, int b,int c){
return a + b + c;
}
public static double sumDouble1(double a, double b){
return a + b;
}
public static double sumDouble2(double a, double b, double c, double d) {
return a + b + c + d;
}
}

方法重载后
有了方法重载,可以将这些功能相似,只是参数不同的方法命名为同一个方法名,在调用JVM会根据参数列表来调用对应的重载方法,这样就简化了开发的复杂度。
public class Demo01MethodOverload {
public static void main(String[] args) {
// 根据传递的参数不同,调用对应的重载方法
System.out.println(sum(10, 20));
System.out.println(sum(10, 20, 30));
System.out.println(sum(11.1, 22.2));
System.out.println(sum(11.1, 22.2, 33.3, 44.4));
}
// 方法名相同,参数列表不同
public static int sum(int a, int b) {
return a + b;
}
public static int sum(int a, int b, int c) {
return a + b + c;
}
public static double sum(double a, double b) {
return a + b;
}
public static double sum(double a, double b, double c, double d) {
return a + b + c + d;
}
}

重载练习
练习1
// 判断哪些方法是重载关系。
public static void open(){} // 正确重载
public static void open(int a){} // 正确重载
static void open(int a,int b){} // 和第9行冲突
public static void open(double a,int b){} // 正确重载
public static void open(int a,double b){} // 和第7行冲突
public void open(int i,double d){} // 和第6行冲突
public static void OPEN(){} // 代码正确,不会报错,但这不是有效重载,名称与第2行不同,区分大小写
public static void open(int i,int j){} // 和第4行冲突

练习2
/*
定义一个方法用来显示不同类型
shitf + F6所有修改所有相同字符
*/
public class Demo04MthodOverloadPrint {
public static void main(String[] args){
myPrinter((byte) 1);
myPrinter((short) 10);
myPrinter(100);
myPrinter(1000L);
myPrinter('A');
myPrinter(1.23F);
myPrinter(1.234);
myPrinter(100 == 200);
myPrinter("Hello,World!");
}
public static void myPrinter(byte num){
System.out.println(num);
}
public static void myPrinter(short num){
System.out.println(num);
}
public static void myPrinter(int num){
System.out.println(num);
}
public static void myPrinter(long num){
System.out.println(num);
}
public static void myPrinter(char ch){
System.out.println(ch);
}
public static void myPrinter(float fl){
System.out.println(fl);
}
public static void myPrinter(double df){
System.out.println(df);
}
public static void myPrinter(boolean truth){
System.out.println(truth);
}
public static void myPrinter(String str){
System.out.println(str);
}
}
方法递归
方法递归,即方法自己调用自己,递归属于一种算法思想,其核心是将一个复杂的问题通过层层的递归变成一个与原问题相似但规模更小的子问题。递归往往可以通过少量的代码来完成多此重复的计算,大大减少了程序的代码量。
递归需要有边界条件,并且需要在过程中不断向该条件靠近,这属于递过程。当满足边界条件后,则返回上一层方法调用处,这属于归过程。
注意:递归的实现一定要具备边界条件,否则会造成栈溢出现象。
递归的实现是利用了栈的数据结构特点,栈是后进先出(LAST IN FIRST OUT)的,也就是先进入栈结构的元素是最后出栈的,就向弹夹一样。而在Java中每次调用方法都会在虚拟机栈的栈顶为该方法开辟一块空间,当前栈帧结束后,会弹栈返回上一级方法调用处,也就是新的栈顶。
递归常见应用
常见的递归应用有求n的阶乘、求第n个斐波那契数、青蛙跳台阶、汉诺塔问题、以及更加复杂的迷宫问题和八皇后问题等。
求n的阶乘
// 求阶乘
public int fact(int n) {
while (n > 1) {
// 利用了求阶乘公式
// n! = n * (n - 1)!
return n * fact(n - 1);
}
return n;
}
@Test
public void testFact() {
int fact = fact(10);
System.out.println(fact); // 3628800
}
第n个斐波那契数
斐波那契数列指的是这样一个数列:
这个数列从第3项开始,每一项都等于前两项之和。
@Test
public void testFib() {
System.out.println(fib(10)); // 55
}
public int fib(int n) {
// 利用了斐波那契数列的公式
// F[n]=F[n-1]+F[n-2](n>=2,F[0]=0,F[1]=1)
if (n < 1) return 0;
if (n < 2) return 1;
return fib(n - 1) + fib(n - 2);
}
青蛙跳台阶问题
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个n级的台阶总共有多少种跳法?
假设:
-
如果只有1级台阶那么只有1种跳法,即只跳一级台阶。
-
如果有2级台阶则有2种跳法,即一次跳一级台阶,或者直接跳两级台阶。
-
如果有3级台阶则有3种跳法:
1)每次跳一级台阶。
2)第一次跳一级台阶,第二次跳两级台阶。
3)第一次跳两级台阶,第二次跳一级台阶。

其实青蛙跳到3级台阶时,只有2种状态,要么是从第1级台阶通过2级跳跳上来,要么从第2级台阶通过1级跳跳上来。
那么假设有n级台阶时,青蛙跳到第n级台阶也只有2种状态,从n-1级台阶通过1级跳到达,或者n-2级台阶通过2级跳到达。
这里应该可以看出来,青蛙跳台阶也是一个斐波那契数列问题,因此按照分析直接实现代码即可。
@Test
public void testFrogJump() {
System.out.println(frogJump(3));
}
// 青蛙跳台阶
public int frogJump(int n) {
if (n < 1) return 0;
// 当n == 1时,只有一种跳法
if (n == 1) return 1;
// 当n == 2时,有两种跳法
if (n == 2) return 2;
// 否则n级台阶就有 F(n-1) + F(n-2)种跳法
return frogJump(n - 1) + frogJump(n - 2);
}
汉诺塔问题
汉诺塔问题是指:一块板上有三根柱子 A、B、C。A 柱上套有 n 个大小不等的圆盘,按照大的在下、小的在上的顺序排列,要把这 n 个圆盘从 A 柱移动到 C 柱上,每次只能移动一个圆盘,移动过程可以借助 B 柱。但在任何时候,任何针上的圆盘都必须保持大盘在下,小盘在上。从键盘输入需移动的圆盘个数,给出移动的过程。
假设只有一个盘,则直接将这个盘从A柱子移动到C柱子

假设有两个盘子则需要将1号盘从a柱移动到b柱,2号盘从a柱移动到c柱,1号盘从b柱移动到c柱

如果是三个盘子,则需要把3号盘子放到C柱,而移动3号盘子之前需要将上面两个盘子移走,并且这两个盘子也不能在c柱上,所以第一步是需要将上面1、2号盘子移动到b柱上,然后将3号盘移动到c柱,接着将1、2号盘子移动到c柱上。我们可以将1、2号盘子看成一个整体。
第一步解决的就是将上面两个盘子经由c柱移动到b柱。
第二步解决的就是将3号盘移动到c柱子(目标柱)
第三步解决的就是将b柱的两个盘子经由a柱移动到c柱,则完成。
第一步的的移动又可以看成是2个盘子的移动,目标柱为b柱。而这又可以划分为1号盘一个盘子的移动,目标柱为c柱。
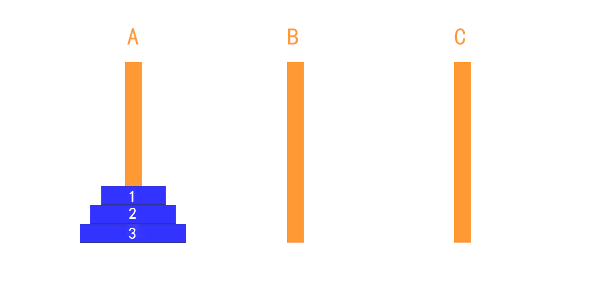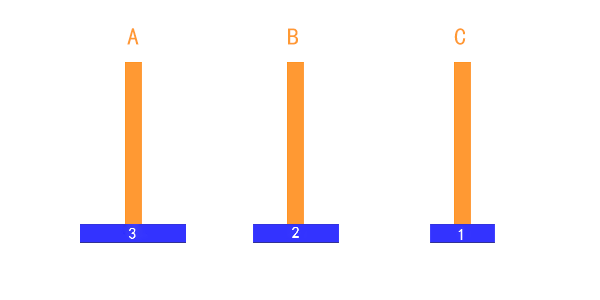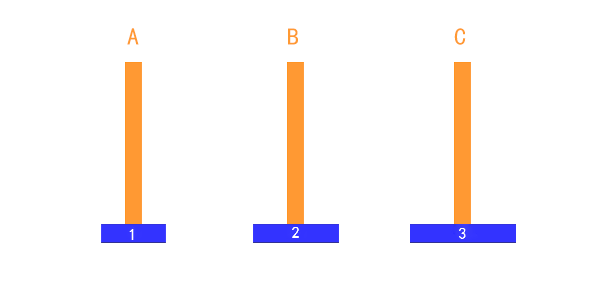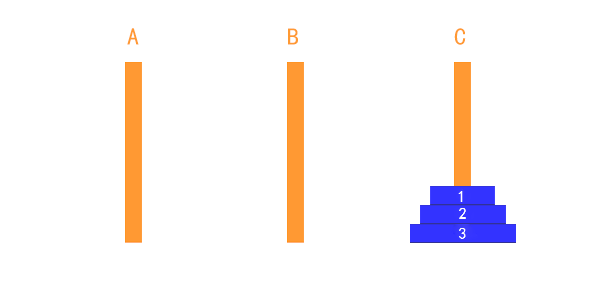
我们不需要深入到每一个步骤,不管有多少个盘子,只需要看成2个部分:
-
最下面的盘子n(需要移动到目标柱)
-
上面的n-1个盘子(需要先从n盘子上经由目标柱移动到中间柱)
接着这n-1个盘子继续拆分…
所以解决汉诺塔问题总体也可以看成三个步骤:
- 将a柱n-1个盘子经由c柱移动到到b柱
- 将a柱盘子移动到c柱
- 将b柱子n-1个盘子经由a柱移动到c柱
@Test
public void test() {
hanoi(3, 'a', 'b', 'c');
}
public static void hanoi(int n, char a, char b, char c) {
// 如果只有一个盘子直接从a柱移动到c柱
if (n == 1)
System.out.println(a + "--->" + c);
else {
// 三步
// 第一步: 将a柱n-1个盘子经由c柱移动到到b柱
hanoi(n - 1, a, c, b);
// 第二步: 将a柱盘子移动到c柱
System.out.println(a + "--->" + c);
// 第三步: 将b柱子n-1个盘子经由a柱移动到c柱
hanoi(n - 1, b, a, c);
}
}
/*
a--->c
a--->b
c--->b
a--->c
b--->a
b--->c
a--->c
*/
迷宫回溯问题
// 测试
public static void main(String[] args) {
int[][] map = new int[8][7];
int row = map.length;
int col = map[0].length;
// 1. 设置地图的墙
// 上下全部置为1
for (int i = 0; i < col; i++) {
map[0][i] = 1;
map[row - 1][i] = 1;
}
// 左右全部置为1
for (int i = 1; i < row - 1; i++) {
map[i][0] = 1;
map[i][col - 1] = 1;
}
// 设置地图中的挡板
map[3][1] = 1;
map[3][2] = 1;
for (int[] arr : map) {
for (int i : arr) {
System.out.print(i + "\t");
}
System.out.println();
}
System.out.println("****************************");
getWay(map, 1, 1);
for (int[] arr : map) {
for (int i : arr) {
System.out.print(i + "\t");
}
System.out.println();
}
}
/**
* 约定:
* 0 表示未经过的点,
* 1 表示墙,
* 2 表示可以经过的点,
* -1 表示不能经过的点。
* <p>
* 思路: 下 --> 右 --> 上 --> 左
* 1. 默认先从(x,y)的位置【向下】探路, 当向下探路遇到 1 或 -1 则表示此路不同, 返回false
* 2. 如果返回false, 接着从(x,y)的位置【向右】探路, 当向下探路遇到 1 或 -1 则表示此路不同, 返回false
* 3. 如果返回false, 接着从(x,y)的位置【向上】探路, 当向下探路遇到 1 或 -1 则表示此路不同, 返回false
* 4. 如果返回false, 接着从(x,y)的位置【向左】探路, 当向下探路遇到 1 或 -1 则表示此路不同, 返回false
* 当所有路径均返回false, 则将当前(x,y)置为3表示此路不通
* 只有当最终递归到终点位置才会返回true, 并回溯
*
* @param map 表示地图
* @param x 表示当前点的横坐标
* @param y 表示当前点的纵坐标
* @return 找到通路返回true, 找不到返回false
*/
public static boolean getWay(int[][] map, int x, int y) {
int row = map.length;
int col = map[0].length;
if (map[row - 2][col - 2] == 2) { // 当终点坐标被置为2, 递归调用结束
return true;
} else {
if (map[x][y] == 0) { // 开始选择路径
map[x][y] = 2; // 先假设本次可以走通
if (getWay(map, x + 1, y)) { // 向下探路, 如果返回值为true, 则本层递归调用不再继续往下直接, 而是直接返回true, 如果返回false, 则会向下继续执行其它几条if,直到抵达终点(终点坐标被置为2)或者本级递归之下的子递归尝试所有路径都返回3表示无路可走。如果最终返回false, 则会执行else语句将当前坐标置为-1,同时也返回false到上一级调用处,上一级调用处也重复一样的操作。
return true;
} else if (getWay(map, x, y + 1)) { // 向右探路
return true;
} else if (getWay(map, x - 1, y)) { // 向上探路
return true;
} else if (getWay(map, x, y - 1)) { // 向左探路
return true;
} else {
// 说明找不到通路
map[x][y] = -1; // 将该点置为-1
return false;
}
} else { // 如果map[x][y] != 0, 则map[x][y] == -1 || 1 || 2; 说明当前点要么不通, 要么已经走过, 则直接return false;
return false;
}
}
}

八皇后问题
感兴趣的可以看这篇博客: 利用递归和回溯解决八皇后问题
代码块
代码块的作用
- 用来初始化类、对象
- 代码块如果有修饰的话,只能使用static修饰
代码块分类
静态代码块
- 内部可以有输出语句。
- 随着类的加载而执行。
- 只会在类加载的时候,执行唯一一次。
- 如果一个类中定义了多个静态代码块,则按照声明的先后顺序执行。
- 静态代码块内只能调用静态的属性。静态的方法,不能调用非静态的结构。
- 作用:初始化静态属性。
非静态代码块
- 内部可以有输出语句。
- 随着对象的创建而执行。
- 每创建一个对象,就执行一次非静态代码块。
- 非静态代码块内可以调用静态的属性、静态的方法。或非静态的属性、非静态的方法。
- 作用:可以在创建对象时,对对象的属性当进行初始化。
注意:静态代码块的执行优先于非静态代码块的执行。
类中对属性可以赋值的位置
- 默认初始化。
- 显示初始化。
- 构造器中初始化。
- 有了对象以后,可以通过"对象.属性" 或 "对象.方法"的方式,进行赋值。
- 在代码块中赋值。
执行的先后顺序: 1 --> 2 / 5 --> 3 --> 4
public class BlockTest {
public static void main(String[] args) {
// 静态代码块随着类的加载而执行
System.out.println("--------------------");
// 非静态代码块随着对象的创建而执行
BlockTest blockTest = new BlockTest();
// 非静态代码块可以执行多次
BlockTest blockTest1 = new BlockTest();
}
int age;
// 静态代码快
static {
System.out.println("hello,static block");
}
// 非静态代码块
{
age = 10;
System.out.println("hello,block");
}
}
// 由父及子,静态先行

