前言+说明

❤️旺仔兄弟们！这个是字节跳动2022届校招生笔试，总共四道编程题！
如果觉得博主分享的不错，希望能留下您的一键❤️三连❤️（点赞+评论+收藏） ，您的支持就是我前进的动力❤️，您的三连对我特别重要。
注明：下述题目只用于学习交流所用，禁止用于商业销售。同时在题解方面也希望大家能提出宝贵建议，共同进步❤️！
❤️此次博文受益于大神“英雄哪里出来”的启发和指点，加了下面文章中的动图。
❤️大神“英雄哪里出来”的算法题图解很漂亮，特别推荐！❤️

一、算法编程题（种树）

时间限制： 3000MS
内存限制： 1048576KB
题目描述：
每年的3月12日是我国的植树节，为了保证树苗的存活率，栽种每颗树苗都需要有一定的间隔，即不能种植在相邻的土地上，否则会发生争夺养分而导致树苗枯萎。你作为一名爱护坏境的Bytedancer分到了一块长度为n乘1的土地，即由n块地组成的一个数组，其中如果种了树的地块用“B”表示，没有种树的地块用“Y”表示，每个地块最多只能种一颗树苗，并且没有相邻地块种了树苗。请你计算出最多还能种多少棵树？

输入描述

第一行输入一个正整数N代表数组大小 1 ≤ N ≤ 10000。
第二行输入数组 bytetreed，其中bytetreed[i] 为 B 或 Y

输出描述

非负整数

示例1

输入：

5
B    Y    Y    Y    B

输出

 1

示例2

输入：

4
Y    Y    Y    B

输出

 1

规则

请尽量在全场考试结束10分钟前调试程序，否则由于密集排队提交，可能查询不到编译结果，点击“调试”亦可保持代码
本编程题不可以使用本地编译器

解题思路：

一、能种树的空缺位置为奇数个时：
       如下图：索引i = 0~14，可种树的索引范围为0 ~ 2、6 ~ 8、12 ~ 14，每段都有3个位置可选。



       1、首段：temp的初始值为-1，i从0指向4。在此过程中能种树的索引范围为：0~2（3个位置），此段最多可种的树num = i/2。

       2、中间段：temp的值变为i的值，即从-1变为4。i从4指向10。在此段能种树的索引范围为：6~8（3个位置），此段最多为(i-temp-2)/2，最多可种的树num = num+(i-temp-2)/2。

       3、末尾段：temp的值再更新为i的值，即从4变为10。i从10指向14。在此段能种树的索引范围为：12~14，此段最多为(i-temp)/2，最多可种的树num = num+(i-temp)/2。

二、能种树的空缺位置为偶数个时：
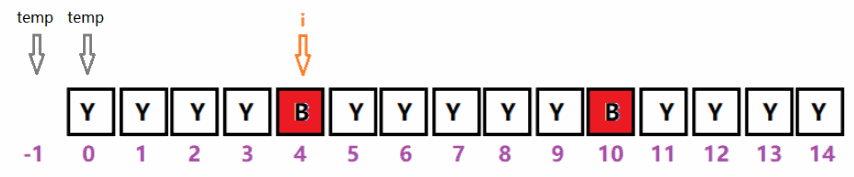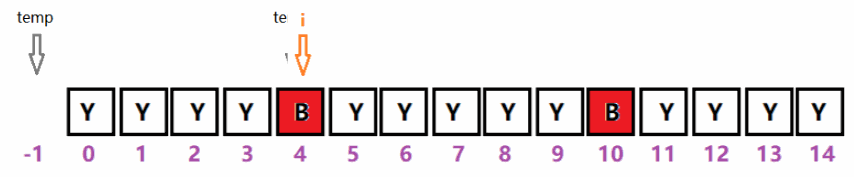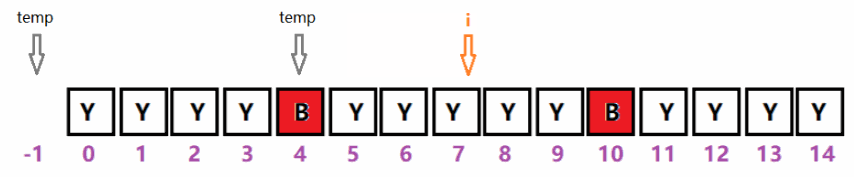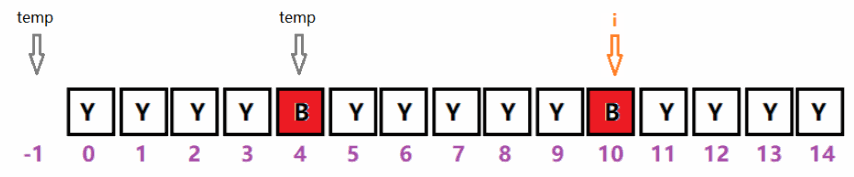
       如下图：索引i = 0~15，可种树的索引范围为0 ~ 1、5 ~ 8、12 ~ 15，每段分别有2、4和4个位置可选。

       1、首段：temp的初始值为-1，i从0指向3。在此过程中能种树的索引范围为：0~1（2个位置），此段最多可种的树num = (i-1)/2。

       2、中间段：temp的值变为i的值，即从-1变为3。i从3指向10。在此段能种树的索引范围为：5~8（4个位置），此段最多为(i-temp-3)/2，最多可种的树num = num+(i-temp-3)/2。

       3、末尾段：temp的值再更新为i的值，即从3变为10。i从10指向15。在此段能种树的索引范围为：12~15（4个位置），此段最多为(i-temp-1)/2，最多可种的树num = num+(i-temp-1)/2。

        综合一二，由于当可以插入的位置为偶数个（即，i-1、i-temp-3和i-temp-1都为偶数）时，首段(i-1)/2 = i/2；中间段(i-temp-3)/2 = (i-temp-2)/2；末尾段(i-temp-1)/2 = (i-temp)/2。
       所以得出奇数段和偶数段的最大种植树苗的树苗通式为：
       首段：num = i/2；
       中间段：num = num+(i-temp-2)/2；
       末尾段：num = num+(i-temp)/2。

参考代码：

import java.util.Scanner;

public class TikTok_Test01 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = Integer.parseInt(sc.nextLine());
        String[] arrs = sc.nextLine().split(" ");
        int ans = plant(arrs);
        System.out.println(ans);
    }
    public static int plant(String[] arrs){
        int ans = 0;
        int n = arrs.length;
        int temp = -1;
        for (int i=0; i<n; i++){
            if (arrs[i].equals("B")){
                if (temp < 0){
                    //最左边的空位置
                    ans += i/2;
                }else {
                    //temp与i之间最多能种的树位置范围为：i-temp-3；
                    //当i-temp-3为奇数时，能种树的数目为：(i-temp-2)/2;
                    //当i-temp-3为偶数时，能种树的数目为：(i-temp-3)/2;
                    //在整数运算中，i-temp-3为偶数时，(i-temp-3)/2=(i-temp-2)/2
                    ans += (i-temp-2)/2;
                }
                //存下种了树的位置索引
                temp = i;
            }
        }
        if (temp < 0){//所有位置都未栽树。当n为偶数时ans=n/2，当n为奇数时ans=（n+1）/2。
            ans += (n+1)/2;
        }else {//在temp之后都是空位，最右边的空位置
            ans += (n-temp-1)/2;
        }
        return ans;
    }
}

二、算法编程题（小A的吃鸡之旅）

时间限制： 2000MS
内存限制： 524288KB
题目描述：
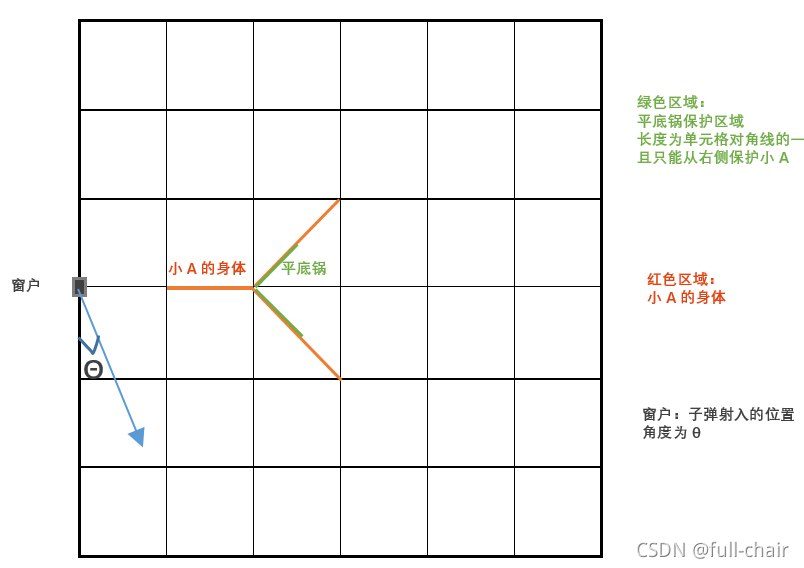
    众所周知，小A不管玩什么游戏都很菜，总是拖队伍的后腿。在小A和朋友组队开黑一款跳伞大逃杀游戏的时候，他总是到处乱闯，胡乱开枪，带领队伍反向吃鸡。为了带领小A赢下游戏，体会到吃鸡的快感，小A的队友们不得己卸下了小A的武器，让小A在房间里好好地“苟着”，其他人出去搜索物资。可小A一点也不老实，总在窗户晃悠，不仅被轰炸得只剩了一丝血，还因此引来窗外狙击手的注意。
    狙击手以一定角度向窗内进行射击，小A听到枪声后吓得直接以“人”字形趴了下去。假设子弹在屋内最多反弹三次（镜面反射，第4次撞击时不会再反弹），而且只要子弹击中或者擦到小A，小A就会阵亡。需要注意的是小A身上带了一个队友留给他的平底锅，如果子弹中了平底锅（包括擦到平底锅）就会陷入平底锅不再反弹，而且也不会对小A造成伤害。房间是一个6×6的格子，可以简单抽象为下图：

输入描述

输入第一行包含一个正整数n（1 ≤ n ≤ 1000），代表有n行输入。
接下来n行每行给出子弹射入的角度θ（0 ≤ θ ≤ π 且 θ ≠ π / 2）的tan值，请你判断每次射击小A能否存活下来。

输出描述

如果一颗子弹未击中小A或者击中平底锅，请在一行内输出“YES”，否则，输出“NO”。

示例1

输入：

3
0
0.8
999.9999

输出

 YES
 YES
 NO

备注

浮点数精度控制在1e-6即可。

规则

请尽量在全场考试结束10分钟前调试程序，否则由于密集排队提交，可能查询不到编译结果，点击“调试”亦可保持代码
本编程题不可以使用本地编译器

解题思路：
采用分类并递归的方式：（大神说这是会让面试官晕倒的方法）。
【参数解释：】
顺时针方向为正
@param x 子弹与墙面相交的横坐标
@param y 子弹与墙面相交的纵坐标
@param tanh 子弹与墙面的夹角
@param n 子弹的反弹次数，初始为0
@return 是否击中小A
1、当x=0时，表示在左侧墙面。
  (1.1)当tanh > 0时有以下情形
    (1.1.1)打中底侧墙面：
      ①重置x,y,n和tanh的值：x=y×tanh、y=0、tanh=1/tanh和n=n+1。
      ②递归调用此方法
    (1.1.2)打中小A，直接返回值true。
    (1.1.3)打中平底锅，直接返回值false。
    (1.1.4)打中右侧墙面：
      ①重置x,y,n和tanh的值：x=6、y=y-6/tanh、tanh=-tanh和n=n+1。
      ②递归调用判断方法
  (1.2)当tanh < 0时有以下情形
    (1.2.1)打中顶侧墙面：
      ①重置x,y,n和tanh的值：x=-(6-y)×tanh、y=6、tanh=1/tanh和n=n+1。
      ②递归调用此方法
    (1.2.2)打中小A，直接返回值true。
    (1.2.3)打中平底锅，直接返回值false。
    (1.2.4)打中右侧墙面：
      ①重置x,y,n和tanh的值：x=6、y=y-6/tanh、tanh=-tanh和n=n+1。
      ②递归调用判断方法
  (1.3)当tanh = 0时,返回false。
2、当y=0时，表示在底侧墙面。
  与1同理。
3、当x=6时，表示在右侧墙面。
  与1同理。
4、当y=6时，表示在顶侧墙面。
  与1同理。

三、算法编程题（有序最大K位数）

时间限制： 2000MS
内存限制： 254288KB
题目描述：
给定N个数组成的序列，其中每个元素都是0~9之间的个数。要求从这个序列中找出K个元素，组成一个K位数，并且这K个元素在原N个数中的相对顺序不变。为这个K位数最大是多少？

输入描述

第一行 输入为N和K（1 ≤ N ≤ 1e⁶,1 ≤ K ≤ N），用空格分隔，其中N为无序序列的长度，K为需要得到的有序数长度。
第二行 依次输入N个个位数，用空格分隔，表示这个序列

输出描述

能够得到的最大K位数的数值（前缀0不输出）

示例1

输入：

2    2    
1    2    

输出

 12

示例2

输入：

8    4    
4    6    2    5    4    1    9    8

输出

 6598

示例3

输入：

6    2    
0    0    0    0    0    0

输出

 0

规则

请尽量在全场考试结束10分钟前调试程序，否则由于密集排队提交，可能查询不到编译结果，点击“调试”亦可保持代码
本编程题不可以使用本地编译器

解题思路：

1、将数组中索引为0 ~ n-k的数存入集合curList，如下图pre与i之间的数值（黄色区域）存入curList集合，并求出curList集合中的最大值6及索引。

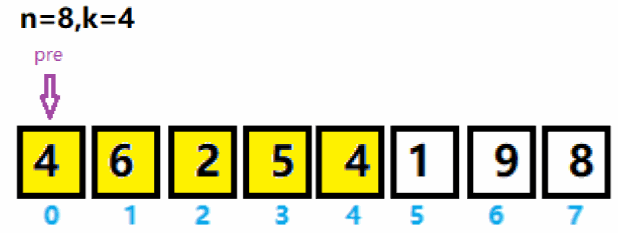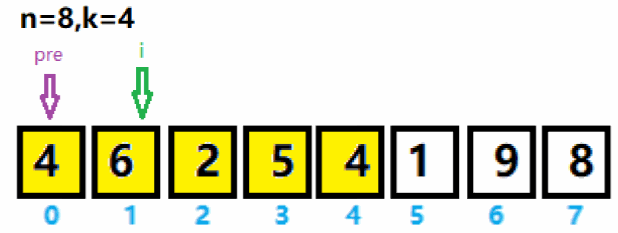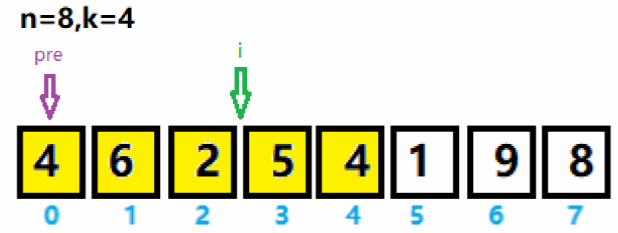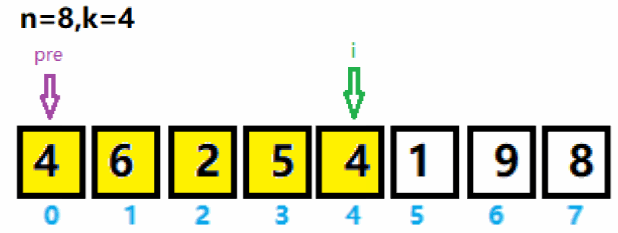
2、将pre指针移到最大值索引后一位，将i向后移动一位。重新将pre与i之间数值（绿色区域）存入curList集合，并求集合里的最大值及索引。与上次求出的最大值6作拼接，得到65。

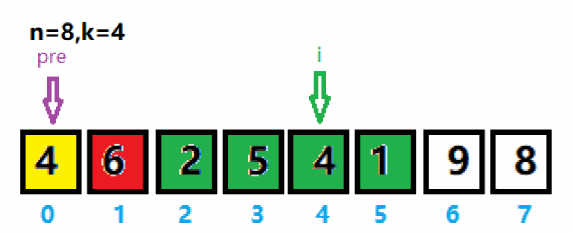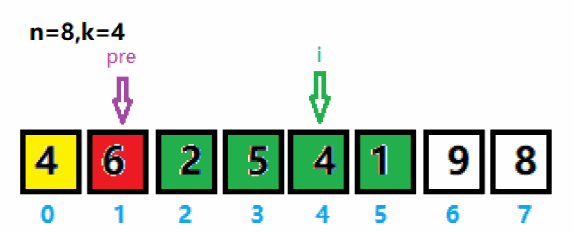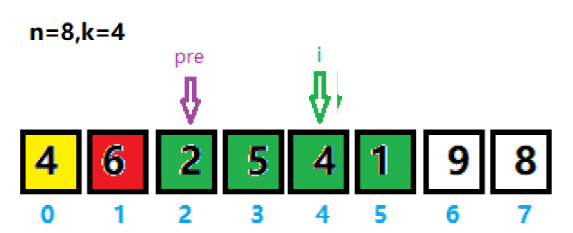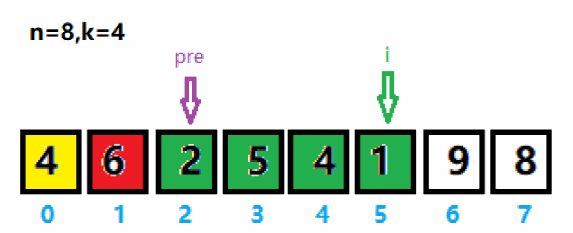
3、重新将pre指针移到最大值5索引后一位，将i向后移动一位。重新将pre与i之间的黄色区域存入curList集合，并求集合里的最大值及索引。与上次求出的最大值65作拼接得到659。

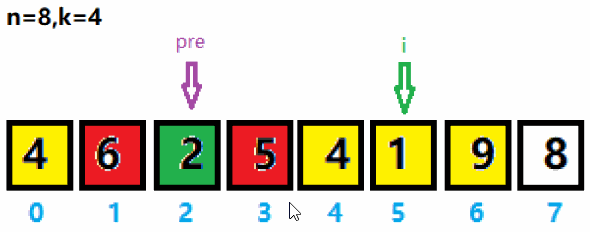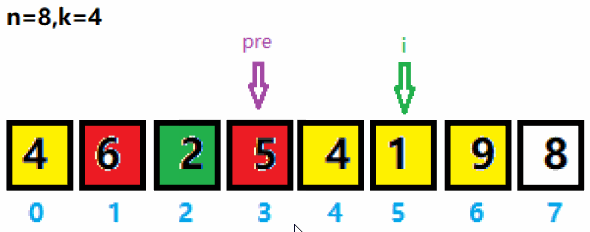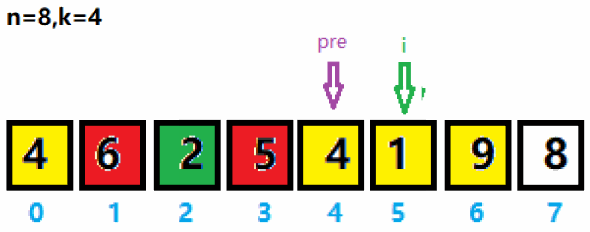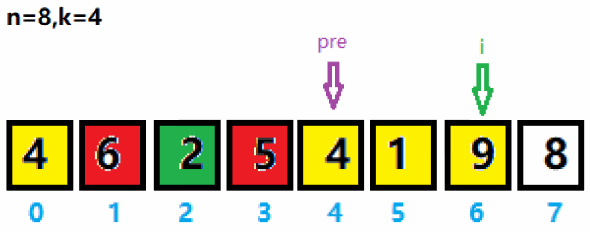
4、依次循环k次。

参考代码：

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;

public class TikTok_Test03 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int k = sc.nextInt();
        int[] arr = new int[n];
        for (int i=0; i<n; i++){
            arr[i] = sc.nextInt();
        }

        int ans = maxNum(arr,k);
        System.out.println(ans);
    }
    public static int maxNum(int[] arr, int k){
        List<Integer> list = new ArrayList<Integer>();
        List<Integer> curList = new ArrayList<Integer>();
        int n = arr.length;
        int pre = -1;
        int max = 0;
        for (int i=0;i<n; i++){
            list.add(arr[i]);
        }

        StringBuilder sb  =  new StringBuilder();
        for (int i=k-1; i>=0; i--){
            for (int j=pre+1;j<n-i; j++){
                curList.add(arr[j]);
            }
            max = Collections.max(curList);
            pre = list.indexOf(max);
            sb.append(max);
            curList.clear();
        }

        int ans = Integer.parseInt(sb.toString());
        return ans;
    }
}

四、算法编程题（测试计划的最大成功率）

时间限制： 2000MS
内存限制： 524288KB
题目描述：
某测试计划有N个测试用例串行执行，现已知条件如下：
1、每个测试用例都是可重复执行的独立事件；
2、用例的执行成功率分别为A1，A2…An （0.9 ≤ An ≤ 1）；
3、每个用例的执行时间均为1秒；
4、每个用例需要事先设置重复执行次数；
5、测试用例需要至少通过一次，则认为该测试用例通过；
6.、如果全部测试用例执行通过，则认为该测试计划执行通过；
请问在M秒内(2N＞M≥N)，该测试计划通过的成功率最大为多少？

输入描述

第一行是一个正整数N（2 ≤ N ≤ 10000）
第二行是N个成功率A1,A2…An，其中0.9 ≤ An ≤ 1
第三行是一个正整数M （2N ＞ M ≥ N）

输出描述

输出一个数字x（保留4位小数），表示最大成功率。

示例1

输入：

5
0.9    0.92    0.94    0.92    0.95
10

输出

 0.9714

规则

请尽量在全场考试结束10分钟前调试程序，否则由于密集排队提交，可能查询不到编译结果，点击“调试”亦可保持代码
本编程题不可以使用本地编译器

解题思路：
【分析】
想要测试通过的成功率最大，则需要排除掉因某个事件失败而导致的整体测试失败；
事件Ai不影响整个测试集测试成功的单个事件最大发生率为：1-（1 - Ai）^m-n （其中：1 ≤ i≤n），可得出最大成功率：

    R_max = ∏ i = 1 m − n ( 1 − （ 1 − A i ） K i ) \prod_{i=1}^{m-n} (1-（1 - Ai）^{Ki}) ∏i=1m−n​(1−（1−Ai）Ki) ∏ j = m − n + 1 m ( A j ) \prod_{j=m-n+1}^{m} (Aj) ∏j=m−n+1m​(Aj)，

     ∑ i = 1 N K i = m − n \sum_{i=1}^N K_i=m-n ∑i=1N​Ki​=m−n 。

【代码思路】
1、将各事件发生的概率k按升序排序。
2、当rep = m-n＞0时：
    2.1、当 1-（1 - A_i）^k ≤ A_i+1，则k++(2 ≤ k ≤ m-n)，rep = rep-1。
    2.2、当 1-（1 - A_i）^k > A_i+1，则i++(1 ≤ i ≤ n-1)。
    2.3、当i=n时，A_n= 1-（1 - A_n）^rep 。
3、当rep=0且i<n时。
    事件的概率不发生改变
4、将所有的事件相乘并保留4位小数输出。

参考代码

import java.util.*;
public class TikTok_Test04 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        List<Double> list = new ArrayList<Double>();
        for (int i=0; i<n; i++){
            list.add(sc.nextDouble());
        }
        int m = sc.nextInt();
        System.out.println(list.toString());
        double ans = maxRate(list,m,n);
        System.out.printf("%.4f",ans);
    }
    public static double maxRate(List<Double> list, int m,int n){
        double ans = 1.0;
        int rep = m-n;
        List<Double> temp = new ArrayList<Double>();
        Collections.sort(list);
        temp.addAll(list);

        for (int i=0; i<n; i++){
            while (rep>0){
                if (i!=n-1){
                    if (temp.get(i)<=temp.get(i+1)){
                        temp.set(i,1-(1-temp.get(i))*(1-list.get(i)));
                    }else {
                        break;
                    }
                }else{
                    temp.set(i,1-(1-temp.get(i))*(1-list.get(i)));
                }
                rep--;
            }
            ans *= temp.get(i);
        }

        return ans;
    }
}