计算机中整数的存储与大小端
文章目录
- 计算机中整数的存储与大小端
- 原码、反码与补码
- 进制
- 二进制的原码、反码和补码
- 大小端模式
原码、反码与补码
进制
日常生活中使用的数字一般都是使用十进制来描述的。而在计算机世界里,数据是以二进制的形式存储的。
关于计数系统和进制,以下是相关资料给出的描述:
在基数b的位置记数系统(其中b是一个正自然数,叫做基数,b个基本符号(或者叫数字)对应于包括0的最小b个自然数。 要产生其他的数,符号在数中的位置要被用到。最后一位的符号用它本身的值,向左一位其值乘以b。一般来讲,若b是基底,我们在b进制系统中的数表示为
的形式,并按次序写下数字a0a1a2a3…ak。这些数字是0到b-1的自然数 。 ------摘录于百度百科
一般情况下,在b进制系统中,数据可以写成以下形式1:

比如,对于整数255,用十进制表示如下:
255
=
2
∗
1
0
2
+
5
∗
1
0
1
+
5
∗
1
0
0
255=2*10^2+5*10^1+5*10^0
255=2∗102+5∗101+5∗100
用八进制表示如下:
255
=
3
∗
8
2
+
7
∗
8
1
+
7
∗
8
0
255=3*8^2+7*8^1+7*8^0
255=3∗82+7∗81+7∗80
用十六进制表示如下:
255
=
15
∗
1
6
1
+
15
∗
1
6
0
255=15*16^1+15*16^0
255=15∗161+15∗160
用二进制表示如下:
255
=
1
∗
2
7
+
1
∗
2
6
+
1
∗
2
5
+
1
∗
2
4
+
1
∗
2
3
+
1
∗
2
2
+
1
∗
2
1
+
1
∗
2
0
255=1*2^7+1*2^6+1*2^5+1*2^4+1*2^3+1*2^2+1*2^1+1*2^0
255=1∗27+1∗26+1∗25+1∗24+1∗23+1∗22+1∗21+1∗20
于是,可以省略权重,统一处理,以达到简记数字的目的。
| 十进制 | 八进制 | 十六进制 | 二进制 |
|---|---|---|---|
| 255 | 377 | FF | 11111111 |
二进制的原码、反码和补码
整数有正负之分。一个整数存储在二进制中也要分正负分别存储,对应于不同的存储规则。整数的二进制表示有三种形式:原码,反码,补码。
- 对于正数而言,其原码、反码和补码相同。直接按照其原始二进制位写出即可,最高位为0。

-
对于负数而言,原码是直接按照原二进制位写出,其最高位是1。
-
符号位不变,其他位按位取反得到反码。
-
反码加1得到补码。

-
整数在内存中是以补码的形式存储的。
-
对整数的运算等操作也是针对补码进行的。
-
而从内存中读取数据时,编译器读取的是转换后的原码。
下面通过一个小案例来说明整数的写入和取出:
int main()
{
int a = -3;
int b = 2;
printf("%d\n", a + b); //以有符号的形式取出并打印
printf("%u\n", a + b); //以无符号的形式取出并打印
return 0;
}
程序运行结果:

程序运行结果显示,不同的读取方式得到的结果完全不同!
下面对这一结果的必然性进行分析解剖:
1、先要把数据a和b以补码的形式存储在内存块中;
2、 直接对补码进行二进制计算;
3、计算得到的直接结果是一个补码;

4、得到计算后的值,需要转换成用户能直接看懂或需要的值,即转换成需要类型的原码。
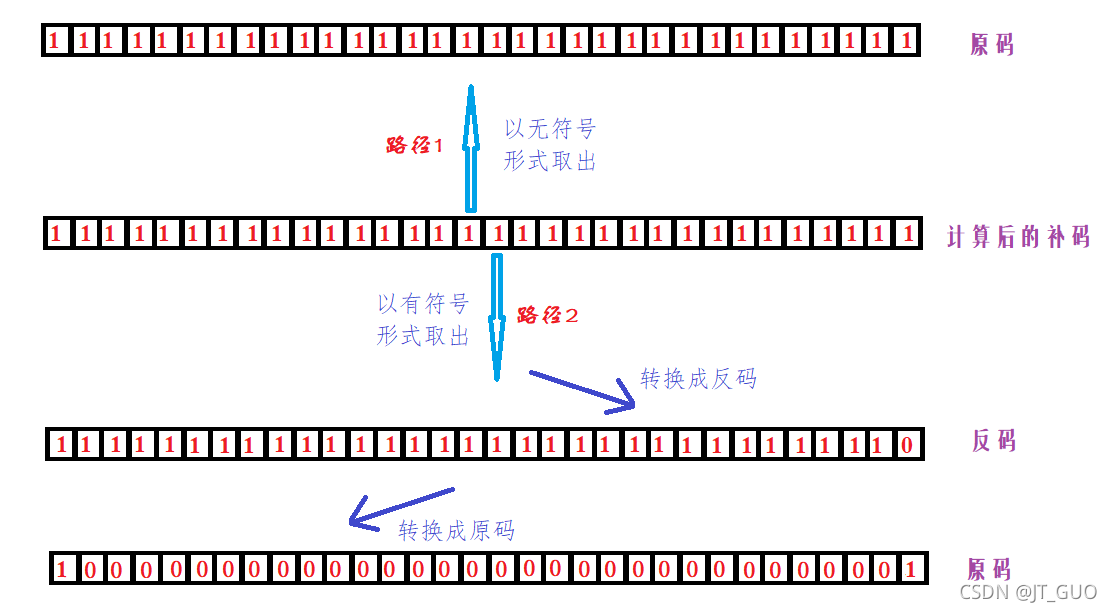
对于直接计算的得到的补码,有两种解读形式供用户选择,即上图所示的路径1和路径2。
- 以无符号整型取出,没有符号位的概念,直接以该补码读出二进制;
- 以有符号位整型取出,最高位是符号位,其中1代表负数,0代表正数,然后按照前面所介绍的正负数的原反补之间的关系转换成二进制原码即可。
据以上分析,第一次打印的是一个非常大的无符号整数,第二次打印的是-1.
大小端模式
对于同一整型数据而言,在内存中存储的排列方式会影响用户读取数据或操纵程序以达到目标需求。
对于大小端的处理也和编译器的实现有关,在C语言中,一般默认是小端; Java是平台无关的,默认是大端。在网络上传输数据普遍采用的都是大端2。
以下是一个案例:
| 十进制 | 二进制 | 十六进制 |
|---|---|---|
| 287,454,020 | 1 0001 0010 0010 0011 0011 0100 0100 | 0x 1122 3344 |
对于这么一个整型数据的存储,在不同的存储模式下,其在内存空间的布局是不一样的。
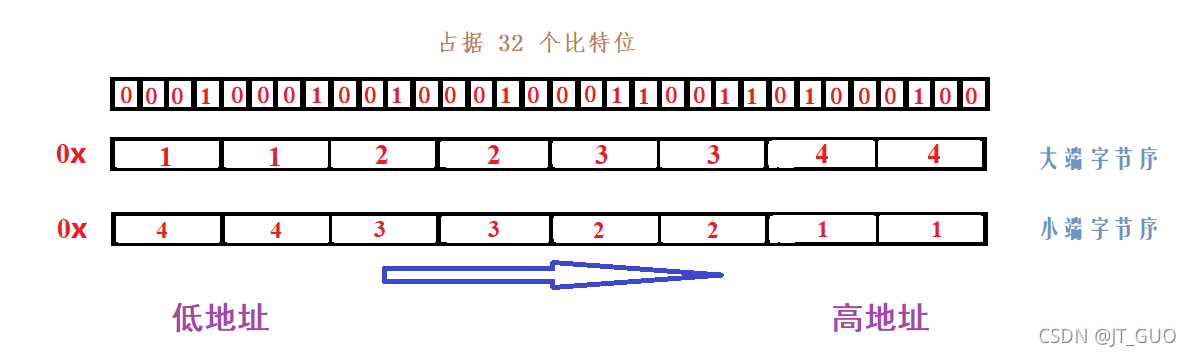
- 把一个数字的低位字节的内容存放在内存的低地址处,把高位字节的内容存放在高地址处的存储方式叫小端字节序存储;
- 反之,把一个数字的低位字节的内容存放在内存的高地址处,把高位字节的内容存放在低地址处的存储方式叫大端字节序存储。
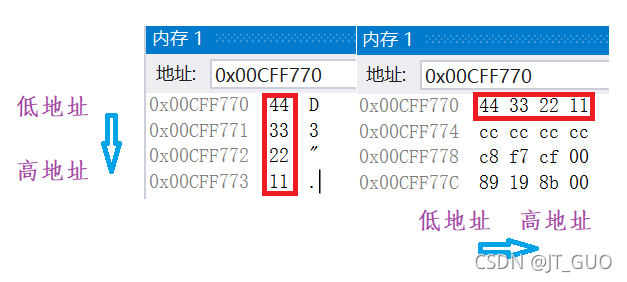
在调试状态下,通过对内存进行监视,可以发现VS编译器对内存地址的使用是小端模式:
好啦,今天的分享到此结束咯,希望小伙伴们都收获满满哦~~

田祖伟, 孙光, 杨素萍. 进制转换的快速方法及应用[J]. 电脑编程技巧与维护, 2008(17):28-29. ↩︎
字节存放顺序:大尾, 小尾. ChinaUnix. ↩︎
