直接跳到末尾 获取粉丝专属福利。
零、前言
「 数据结构 」 和 「 算法 」 是密不可分的,两者往往是「 相辅相成 」的存在,所以,在学习 「 数据结构 」 的过程中,不免会遇到各种「 算法 」。
数据结构 常用的操作一般为:「 增 」「 删 」「 改 」「 查 」。基本上所有的数据结构都是围绕这几个操作进行展开的。
那么这篇文章,作者将用 「 十张动图 」 来阐述一种 「 一端插入 」「 两端删除 」 的数据结构
「 单调队列 」


单调队列的操作浓缩为以下一张图:

看不懂没有关系,我会把它拆开来一个一个讲,首先来看一下今天要学习的内容目录。
文章目录
- 零、前言
- 一、滑动窗口
- 1、引例
- 2、暴力求解
- 3、区间最值
- 4、容器抽象
- 二、FIFO 队列
- 1、FIFO 队列的概念
- 1)队列的定义
- 2)队首
- 3)队尾
- 2、FIFO 队列的接口
- 1)数据入队
- 2)数据出队
- 3)清空队列
- 4)获取队首数据
- 5)获取队列元素个数
- 6)队列的判空
- 3、队列的实现
- 三、双端队列
- 1、双端队列的概念
- 1)双端队列的定义
- 2)队首
- 3)队尾
- 2、双端队列的接口
- 1)队首入队
- 2)队尾入队
- 3)队首出队
- 4)队尾出队
- 5)清空队列
- 6)获取队列元素个数
- 7)队列判空
- 8)获取队首元素
- 9)获取队尾元素
- 3、双端队列的实现
- 四、单调队列
- 1、定义
- 2、询问
- 3、删除
- 4、插入
- 5、性质
- 1)保序性
- 2)下标存储
- 3)单调性
- 五、单调队列的应用
- 1、最值问题
- 1)问题描述
- 2)思路分析
- 3)源码详解
- 2、DP 优化
- 1)问题描述
- 2)思路分析
- 3)源码详解
- 3、前缀和
- 1)问题描述
- 2)思路分析
- 3)源码详解
- 六、单调队列相关题集整理
- 七、粉丝专属福利
一、滑动窗口
1、引例
【例题1】给定一个长度为 n ( n ≤ 1 0 5 ) n(n \le 10^5) n(n≤105) 整数数组 a i a_i ai,有一个大小为 k ( k ≤ 1 0 5 ) k(k \le 10^5) k(k≤105) 的滑动窗口从数组的最左侧移动到数组的最右侧。只能看到在滑动窗口内的 k k k 个数字。滑动窗口每次只向右移动一位。返回 每个滑动窗口 的最大值。
2、暴力求解
看到这个问题,最简单的思路就是:枚举一个起点 s s s,然后记录区间 [ s , s + k − 1 ] [s, s + k-1] [s,s+k−1] 内的最大值。枚举起点的时间复杂度为 O ( n ) O(n) O(n),记录区间最值的时间复杂度为 O ( k ) O(k) O(k),所以总的时间复杂度为 O ( n k ) O(nk) O(nk),对于这个问题的数据量,最大的数据量达到了 1 0 10 10^{10} 1010 量级,所以这个做法是行不通的。
3、区间最值
这个问题是个经典的区间最值问题,可以通过 ST表 (Sparse Table, 稀疏表) 求解,时间复杂度为 O ( n l o g 2 k ) O(nlog_2k) O(nlog2k),除了 ST表,还可以采用 线段树 求解区间最值,时间复杂度也为 O ( n l o g 2 k ) O(nlog_2k) O(nlog2k)。当然,这两块内容都不是本文讨论的重点,如果对 ST表 感兴趣,可以参考以下文章:夜深人静写算法(六)- RMQ。对线段树感兴趣,可以参考以下文章:夜深人静写算法(四十一)- 线段树。
4、容器抽象
本文将介绍一种
O
(
n
)
O(n)
O(n) 的算法。它将会用到一种数据结构 —— 单调队列。
在这个问题中,两个相邻的滑动窗口,实际上只相差两个元素,如下图所示:

假设,我们提供了一种容器,这个容器能够支持三种操作:
1)【询问】通过 O ( 1 ) O(1) O(1) 的时间,获取容器中元素的最大值。
2)【删除】通过 O ( 1 ) O(1) O(1) 的时间,删除元素;
3)【插入】通过 O ( 1 ) O(1) O(1) 的时间,插入元素;
那么,我们只要不断的移动滑动窗口,每一次移动,删除一个元素,插入另一个元素,并且记录下最大值,那么,每一次滑动,只需要三步
O
(
1
)
O(1)
O(1) 的操作。总共
n
n
n 次滑动,只需要
O
(
n
)
O(n)
O(n) 的时间复杂度就能解决这个问题。
这种容器存在吗?让我们首先简单了解一下 FIFO 队列 和 双端队列,如果你对 以上两种数据结构 已经 了如指掌,则可以跳过相关内容,直接观看 👉🏻单调队列👈🏻 部分。
二、FIFO 队列
1、FIFO 队列的概念
1)队列的定义
队列 是仅限在 一端 进行 插入,另一端 进行 删除 的 线性表。
队列 又被称为 先进先出 (First In First Out) 的线性表,简称 FIFO 队列。

2)队首
允许进行元素删除的一端称为 队首。如下图所示:

3)队尾
允许进行元素插入的一端称为 队尾。如下图所示:

2、FIFO 队列的接口
1)数据入队
队列的插入操作,叫做 入队。它是将 数据元素 从 队尾 进行插入的过程,如图所示,表示的是 插入 两个数据(绿色 和 蓝色)的过程:

2)数据出队
队列的删除操作,叫做 出队。它是将 队首 元素进行删除的过程,如图所示,表示的是 依次 删除 两个数据(红色 和 橙色)的过程:

3)清空队列
队列的清空操作,就是一直 出队,直到队列为空的过程,当 队首 和 队尾 重合时,就代表队尾为空了,如图所示:

4)获取队首数据
对于一个队列来说只能获取 队首 数据,一般不支持获取 其它数据。
5)获取队列元素个数
队列元素个数一般用一个额外变量存储,入队 时加一,出队 时减一。这样获取队列元素的时候就不需要遍历整个队列。通过 O ( 1 ) O(1) O(1) 的时间复杂度获取队列元素个数。
6)队列的判空
当队列元素个数为零时,就是一个 空队,空队 不允许 出队 操作。
3、队列的实现
队列的实现,可以参考以下这篇文章:❤️《画解数据结构》九张动图,画解队列❤️。
三、双端队列
1、双端队列的概念
1)双端队列的定义
双端队列 是一种具有 队列 和 栈 的性质的数据结构,是我们常说的 deque(double-ended queue),是一种限定 插入 和 删除 操作在表的两端进行的线性表。这两端分别被称为 队首 和 队尾。

2)队首
双端队列的一端被称为 队首,如下图所示:

3)队尾
双端队列的另一端被称为 队尾,如下图所示:

2、双端队列的接口
1)队首入队
队列的插入操作,叫做 入队。
队首入队 就是将 数据元素 从 队首 进行插入的过程。如图所示,表示的是在队首 插入 一个蓝色数据的过程:

2)队尾入队
队尾入队 就是将 数据元素 从 队尾 进行插入的过程。如图所示,表示的是在队尾 插入 一个紫色数据的过程:

3)队首出队
队列的删除操作,叫做 出队。
队首出队 是将 队首 元素进行删除的过程,如图所示,表示的是在队首 删除 一个蓝色数据的过程:

4)队尾出队
队尾出队 是将 队尾 元素进行删除的过程,如图所示,表示的是在队尾 删除 一个紫色数据的过程:

5)清空队列
队列的清空操作,就是一直 出队,直到队列为空的过程,当 队首 和 队尾 正好错开一个位置时,就代表队尾为空了,如图所示,细心的读者会发现,队尾 和 队首 错开了一个位置:

6)获取队列元素个数
队列元素个数一般用一个额外变量存储,入队 时加一,出队 时减一。这样获取队列元素的时候就不需要遍历整个队列。通过 O ( 1 ) O(1) O(1) 的时间复杂度获取队列元素个数。
7)队列判空
当队列元素个数为零时,就是一个 空队,空队 不允许 出队 操作。
8)获取队首元素
队首指针 指向的数据被称为 队首元素,可以通过 O ( 1 ) O(1) O(1) 的时间复杂度来获取。
9)获取队尾元素
队尾指针 指向的数据被称为 队尾元素,可以通过 O ( 1 ) O(1) O(1) 的时间复杂度来获取。
3、双端队列的实现
需要了解双端队列的实现,可以参考如下文章:❤️《画解数据结构》十张动图,画解双端队列❤️
四、单调队列
单调队列 就是能够完美支持下面三种操作的一种容器:
1)【询问】通过 O ( 1 ) O(1) O(1) 的时间,获取容器中元素的最大值。
2)【删除】通过 O ( 1 ) O(1) O(1) 的时间,删除元素;
3)【插入】通过 O ( 1 ) O(1) O(1) 的时间,插入元素;
1、定义
单调队列是一个限制只能 队尾插入,但是可以 两端删除 的 双端队列 。单调队列 存储的元素值,是从 队首 到 队尾 呈单调性的(要么单调递增,要么单调递减)。
对于求解最大值的问题,则需要维护一个 单调递减 的队列。

如图所示,⑨ 为原先的 队首元素,执行 队首删除(出队) 操作以后,⑥ 成为新的 队首元素;而在队尾执行插入④这个元素的时候,为了保持单调性,需要将①②依次从队尾删除;当队尾执行插入②这个元素的时候,满足单调性。
2、询问
由于单调队列是单调递减的,所以队首元素 最大,直接 O ( 1 ) O(1) O(1) 获取队首元素。

如图所示,head 指向 队首元素,直接获取,由于这是一个单调递减队列,所以得到的,就是最大值。
3、删除
删除分为 队首删除 和 队尾删除。
队首删除即直接队首元素出队,
O
(
1
)
O(1)
O(1) 即可完成操作。如图所示:

队尾删除 一般是配合 队尾插入 进行的。我们接着往下看。
4、插入
在进行 队尾插入 的时候,我们往往需要明白一个重要的点,就是需要保证它 单调递减 的性质,所以如果 队尾元素
≤
\le
≤ 插入元素 ,则当前的 队尾元素 是需要执行删除操作的(也就是上文提到的 队尾删除),直到满足 队尾元素
>
\gt
> 插入元素,才能真正执行 插入 操作。
这样才能保证,执行 队尾插入 后,单调队列仍然是 单调递减 的。插入过程,虽然伴随着元素的删除,但是每个元素至多被 插入一次 和 删除一次,所以均摊时间复杂度还是
O
(
1
)
O(1)
O(1) 的。

如图所示,在队尾执行插入④这个元素的时候,为了保持单调性,需要将①②依次从队尾删除;当队尾执行插入②这个元素的时候,满足单调性,所以直接执行插入操作。
5、性质
1)保序性
由于单调队列执行插入的时候,一定是从队尾进行插入,所以单调队列中的数据,从队首到队尾的顺序,一定是和原序列严格保序的;
2)下标存储
为了让单调队列的数据足够干净,在单调队列中,一般存储 原序列的下标 即可,而不需要存储原序列的值,根据保序性,存储的下标一定是单调递增的;
3)单调性
单调队列中的元素是 原序列的下标,对应到原序列时,根据求解问题的不同,当需要求最大值时,它是单调递减的;当需要求最小值时,它是单调递增的;
五、单调队列的应用
1、最值问题
1)问题描述
继续回到上文提到的滑动窗口中的最大值问题。
【例题1】给定一个长度为 n ( n ≤ 1 0 5 ) n(n \le 10^5) n(n≤105) 整数数组 A i A_i Ai,有一个大小为 k ( k ≤ 1 0 5 ) k(k \le 10^5) k(k≤105) 的滑动窗口从数组的最左侧移动到数组的最右侧。只能看到在滑动窗口内的 k k k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值。
2)思路分析
我们要实现的,就是把原序列
A
A
A 中的元素逐个执行单调队列的 插入 操作。当 插入 的原序列的下标为
i
i
i 时,期望是单调队列中的元素从 队首 到 队尾 都在原序列的区间
(
i
−
k
,
i
]
(i-k, i]
(i−k,i] 范围内(也就是以
i
i
i 为右端点,长度为
k
k
k 的区间内),且对应到原序列的值单调递减,这样每次插入完毕,就可以在
O
(
1
)
O(1)
O(1) 的时间内,从队首获取到最大值(即区间
(
i
−
k
,
i
]
(i-k, i]
(i−k,i] 内的最大值)。
为什么是单调递减?而不是单调递增?
对于每个需要插入的下标
i
i
i,队尾的元素为原序列的下标
j
j
j,则根据保序性,一定能够满足
j
<
i
j \lt i
j<i,如果对应到原序列中,满足
A
j
≤
A
i
A_j \le A_i
Aj≤Ai,那么
A
j
A_j
Aj 不会比
A
i
A_i
Ai 更优,原因是:对于区间
(
i
−
k
,
i
]
(i-k, i]
(i−k,i] 来说,
A
i
A_i
Ai 一定在区间内,而
A
j
A_j
Aj 则未必,也就是说 下标
j
j
j 没必要存储到单调队列中。于是对于单调队列中的存储的元素
i
1
<
i
2
<
.
.
.
<
i
n
i_1 < i_2 < ... < i_n
i1<i2<...<in 需要满足:
A
i
1
>
A
i
2
>
.
.
.
>
A
i
n
A_{i_1} > A_{i_2} > ... > A_{i_n}
Ai1>Ai2>...>Ain,即 维护一个单调递减的队列。
实际执行过程中,每次插入后,队尾元素 减去 队首元素 必须小于等于
k
−
1
k-1
k−1,一旦超过
k
−
1
k-1
k−1,就要从队首不断出队了。
3)源码详解
int* maxSlidingWindow(int* nums, int numsSize, int k, int* returnSize){
int i, pos = 0;
struct Queue *q = (struct Queue*)malloc( sizeof(struct Queue)); // (1)
int *ret = (int *)malloc( (numsSize - k + 1) * sizeof(int) ); // (2)
*returnSize = numsSize - k + 1; // (3)
for(i = 0; i < numsSize; ++i) {
while( !QueueIsEmpty(q) && i - QueueGetFront(q) > k-1 ) // (4)
QueueDequeueFront(q);
while( !QueueIsEmpty(q) && nums[ QueueGetRear(q) ] <= nums[i]) // (5)
QueueDequeueRear(q);
QueueEnqueueRear(q, i); // (6)
if(i >= k - 1)
ret[i - k + 1] = nums[ QueueGetFront(q) ]; // (7)
}
return ret;
}
- ( 1 ) (1) (1) 申请一个队列的内存空间;
- ( 2 ) (2) (2) 申请 返回数组 需要的内存空间;
-
(
3
)
(3)
(3) 设置 返回数组 的
size; - ( 4 ) (4) (4) 时刻保持 队尾元素 减去 队首元素 小于等于 k − 1 k-1 k−1,不满足时,队首出队;
- ( 5 ) (5) (5) 单调队列 元素存的是原序列 下标,所以需要索引到值,且值 单调递减,不满足时,队尾出队;
- ( 6 ) (6) (6) 满足以上两个条件以后,将原序列的下标 i i i 插入单调队列(即 队尾入队);
- ( 7 ) (7) (7) 取队首,索引原数组后,就是区间 ( i − k , i ] (i-k, i] (i−k,i] 的最大值;
2、DP 优化
1)问题描述
【例题2】给定一个下标从 0 开始,元素个数为 n ( n ≤ 1 0 5 ) n(n \le 10^5) n(n≤105) 的整数数组 a a a 和一个整数 k k k 。开始在下标 0 处。每一步,最多可以往前跳 k k k 步,但不能跳出数组的边界。也就是说,可以从下标 i i i 跳到 [ i + 1 , m i n ( n − 1 , i + k ) ] [i + 1, min(n - 1, i + k)] [i+1,min(n−1,i+k)] 包含 两个端点的任意位置。
目标是到达数组最后一个位置(下标为 n − 1 n - 1 n−1 ),得分 为经过的所有数字之和,求得分的最大值。
2)思路分析
比较容易想到的是动态规划,假设跳到位置
i
i
i 的最大值是
d
p
[
i
]
dp[i]
dp[i], 那么一定是从
[
i
−
k
,
i
−
1
]
[i-k, i-1]
[i−k,i−1] 中的某个位置跳过来的,可以得到状态转移方程如下:
d
p
[
i
]
=
a
i
+
m
a
x
(
d
p
[
i
−
1
]
,
.
.
.
,
d
p
[
i
−
k
]
)
dp[i] = a_i + max(dp[i-1], ..., dp[i-k])
dp[i]=ai+max(dp[i−1],...,dp[i−k]) 但是这一步的问题在于,数组长度为
n
n
n 时,每次状态转移的时间为
O
(
k
)
O(k)
O(k),所以整個算法的时间复杂度为
O
(
n
k
)
O(nk)
O(nk)。所以我们需要想办法将
m
a
x
(
d
p
[
i
−
1
]
,
.
.
.
,
d
p
[
i
−
k
]
)
max(dp[i-1], ..., dp[i-k])
max(dp[i−1],...,dp[i−k]) 这步操作化为
O
(
1
)
O(1)
O(1)。
维护一个单调递减的队列,这样就能通过
O
(
1
)
O(1)
O(1) 的时间找到从队首找到最大值。单调队列始终保持
d
p
[
.
.
.
]
dp[...]
dp[...] 的元素在队列中是单调递减的。对于队列中的两个元素,下标位置为
j
<
i
j < i
j<i, 如果
d
p
[
j
]
≤
d
p
[
i
]
dp[j] \le dp[i]
dp[j]≤dp[i],则
d
p
[
j
]
dp[j]
dp[j] 不能放入 单调队列中,因为它不会比
d
p
[
i
]
dp[i]
dp[i] 更优。并且时刻保证,当前元素插入单调队列之后,单调队列队列的 队首元素
x
x
x,满足
i
−
x
≤
k
i - x \le k
i−x≤k。
3)源码详解
int dp[maxn];
int maxResult(int* nums, int numsSize, int k){
int i;
struct Queue *q = (struct Queue *) malloc (sizeof(struct Queue));
dp[0] = nums[0]; // (1)
QueueClear(q);
QueueEnqueue(q, 0); // (2)
for(i = 1; i < numsSize; ++i) { // (3)
while(!QueueIsEmpty(q) && i - QueueGetFront(q) > k) // (4)
QueueDequeueFront(q);
dp[i] = nums[i] + dp[ QueueGetFront(q) ]; // (5)
while(!QueueIsEmpty(q) && dp[ QueueGetRear(q) ] <= dp[i]) // (6)
QueueDequeueRear(q);
QueueEnqueueRear(q, i); // (7)
}
return dp[numsSize-1]; // (8)
}
- ( 1 ) (1) (1) 初始化位置;
- ( 2 ) (2) (2) 初始情况,队列里面只有 0 这个位置;
- ( 3 ) (3) (3) 从第 1 个位置开始计算 d p [ i ] dp[i] dp[i];
- ( 4 ) (4) (4) 确保计算过程中的 区间范围在 [ i − 1 , i − k ] [i-1, i-k] [i−1,i−k] 范围内;
-
(
5
)
(5)
(5) 利用单调队列性质,队首
dp[ QueueGetFront(q) ]必然最大,直接进行状态转移; - ( 6 ) (6) (6) d p [ i ] dp[i] dp[i] 一定会插入单调队列,所以比它小的都应该出队;
- ( 7 ) (7) (7) 执行插入操作;
- ( 8 ) (8) (8) 返回一个位置的计算结果;
3、前缀和
1)问题描述
【例题3】返回数组 A A A 的最短的非空连续子数组的长度,该子数组的和至少为 k k k。如果没有和至少为 k k k 的非空子数组,返回 − 1 -1 −1。
2)思路分析
前缀和预处理:令
s
u
m
i
sum_i
sumi 代表
A
i
A_i
Ai 的前缀和,对于一段左开右闭子数组
(
t
,
i
]
(t, i]
(t,i],
s
u
m
i
−
s
u
m
t
sum_i - sum_t
sumi−sumt 就是这段子数组的和,其中
−
1
≤
t
<
i
-1 \le t \lt i
−1≤t<i,并且必须满足子数组和
s
u
m
i
−
s
u
m
t
≥
k
sum_i - sum_t \ge k
sumi−sumt≥k。
单调性的思考:对于两个下标
t
1
<
t
2
t_1 \lt t_2
t1<t2, 如果
s
u
m
t
1
≥
s
u
m
t
2
sum_{t_1} \ge sum_{t_2}
sumt1≥sumt2,则
s
u
m
t
1
sum_{t_1}
sumt1 不会比
s
u
m
t
2
sum_{t_2}
sumt2 更优,所以,我们只需要维护一个
s
u
m
sum
sum 值单调递增的单调队列;
维护单调队列:单调队列的队首一定是
s
u
m
sum
sum 值最小的,
s
u
m
i
−
s
u
m
q
u
e
u
e
f
r
o
n
t
≥
k
sum_i - sum_{queuefront} \ge k
sumi−sumqueuefront≥k,则记录
i
−
q
u
e
u
e
f
r
o
n
t
i - queuefront
i−queuefront 作为一个候选解,并且弹出队首;
实际落地方案:然后只需要枚举
i
i
i,维护
s
u
m
i
sum_i
sumi 的单调队列,且单调队列插入的是前缀和的下标值,候选最优值
i
−
q
u
e
u
e
f
r
o
n
t
i - queuefront
i−queuefront 用于和最终最优值进行比较取小者,不存在候选解则返回
−
1
-1
−1。
3)源码详解
struct Queue q;
int sum[maxn];
int getValue(int index) {
if(index == -1) {
return 0;
}
return sum[index]; // (1)
}
int shortestSubarray(int* nums, int numsSize, int k){
int i;
int len, minlen;
for(i = 0; i < numsSize; ++i) {
sum[i] = nums[i];
if(i)
sum[i] += sum[i-1]; // (2)
}
QueueClear(&q);
QueueEnqueue(&q, -1); // (3)
minlen = numsSize + 1;
for(i = 0; i < numsSize; ++i) {
while(!QueueIsEmpty(&q) && getValue( QueueGetRear(&q) ) >= getValue(i))
QueueDequeueRear(&q); // (4)
while(!QueueIsEmpty(&q) && getValue(i) - getValue( QueueGetFront(&q) ) >= k) {
len = i - QueueGetFront(&q);
if (len < minlen) {
minlen = len; // (5)
}
QueueDequeueFront(&q);
}
QueueEnqueue(&q, i);
}
return minlen == numsSize + 1 ? -1 : minlen;
}
- ( 1 ) (1) (1) 需要考虑前缀和存在 s u m [ − 1 ] sum[-1] sum[−1] 的情况,为了数组下标不越界,封装一个函数返回前缀和;
- ( 2 ) (2) (2) 初始化前缀和;
- ( 3 ) (3) (3) 相当于插入一个 s u m [ − 1 ] sum[-1] sum[−1];
- ( 4 ) (4) (4) 保证一个单调递增的队列;
- ( 5 ) (5) (5) 找到一个可行解;
六、单调队列相关题集整理
👉🏻👉🏻👉🏻 队列 / 单调队列 相关题集整理

关于 「 单调队列 」 的内容到这里就结束了。
如果还有不懂的问题,可以通过 「 电脑版主页 」找到作者的「 联系方式 」 ,线上沟通交流。
有关🌳《画解数据结构》🌳 的源码均开源,链接如下:《画解数据结构》

相信看我文章的大多数都是「 大学生 」,能上大学的都是「 精英 」,那么我们自然要「 精益求精 」,如果你还是「 大一 」,那么太好了,你拥有大把时间,当然你可以选择「 刷剧 」,然而,「 学好算法 」,三年后的你自然「 不能同日而语 」。
那么这里,我整理了「 几十个基础算法 」 的分类,点击开启:
如果链接被屏蔽,或者有权限问题,可以私聊作者解决。
大致题集一览:

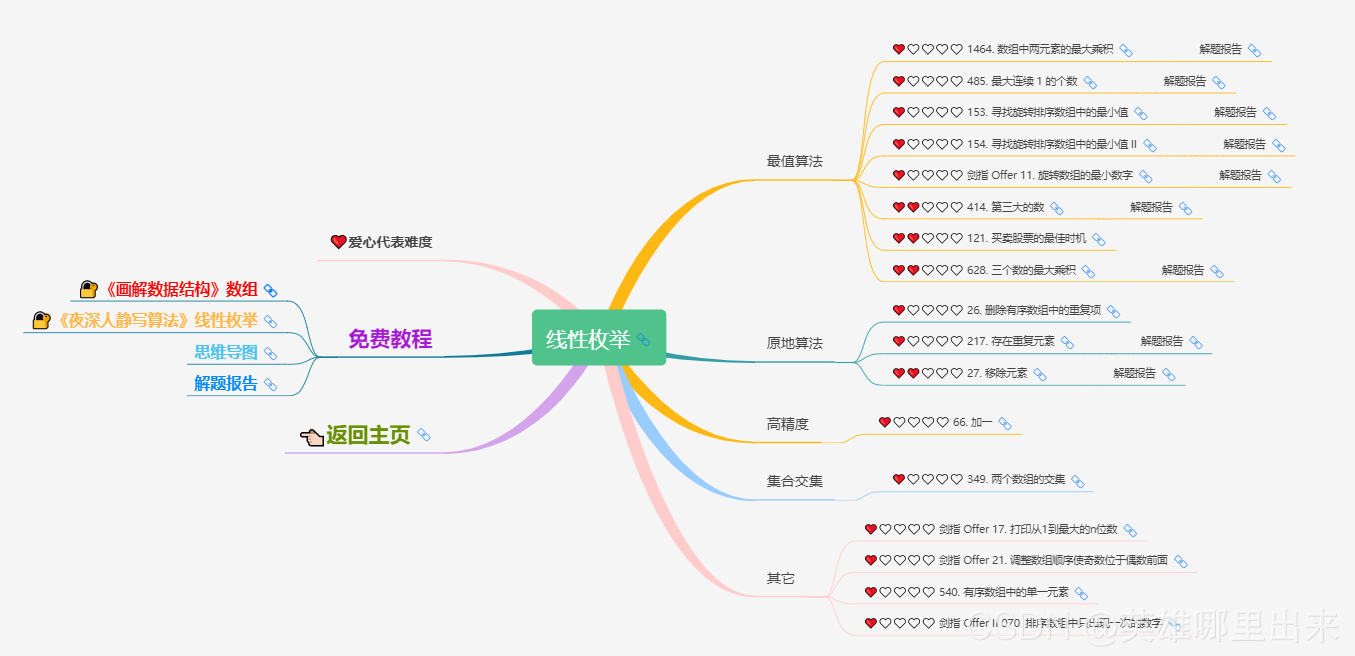
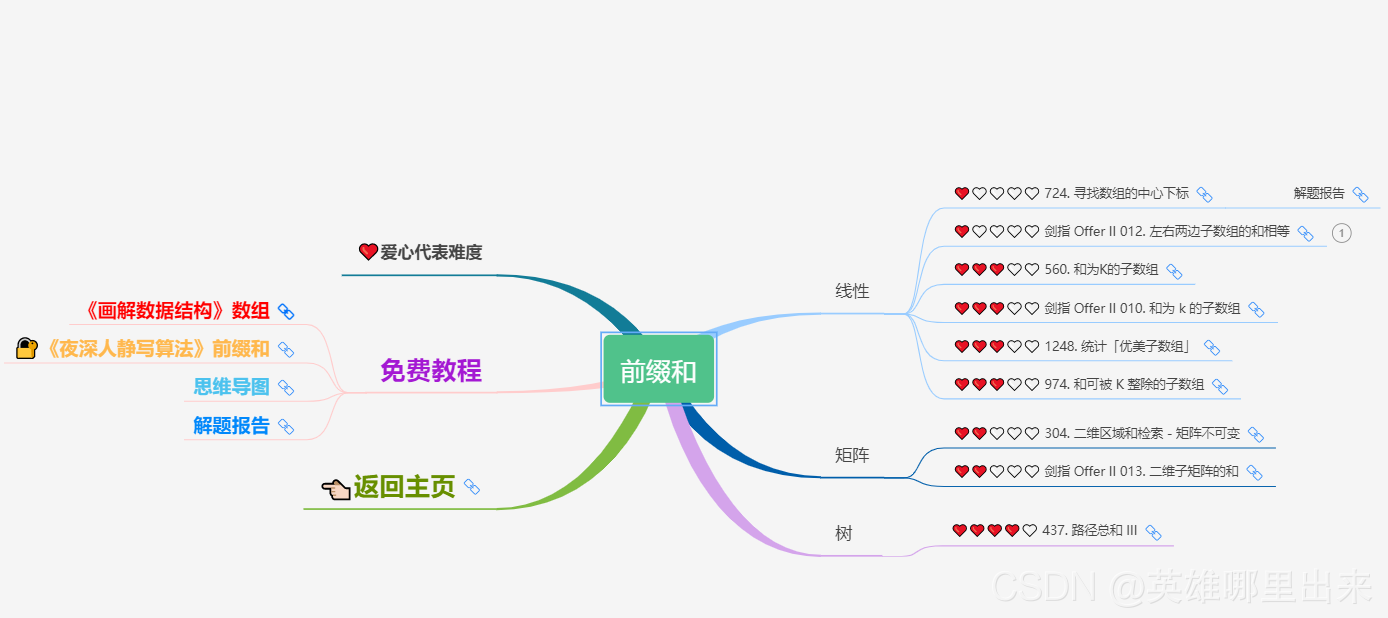
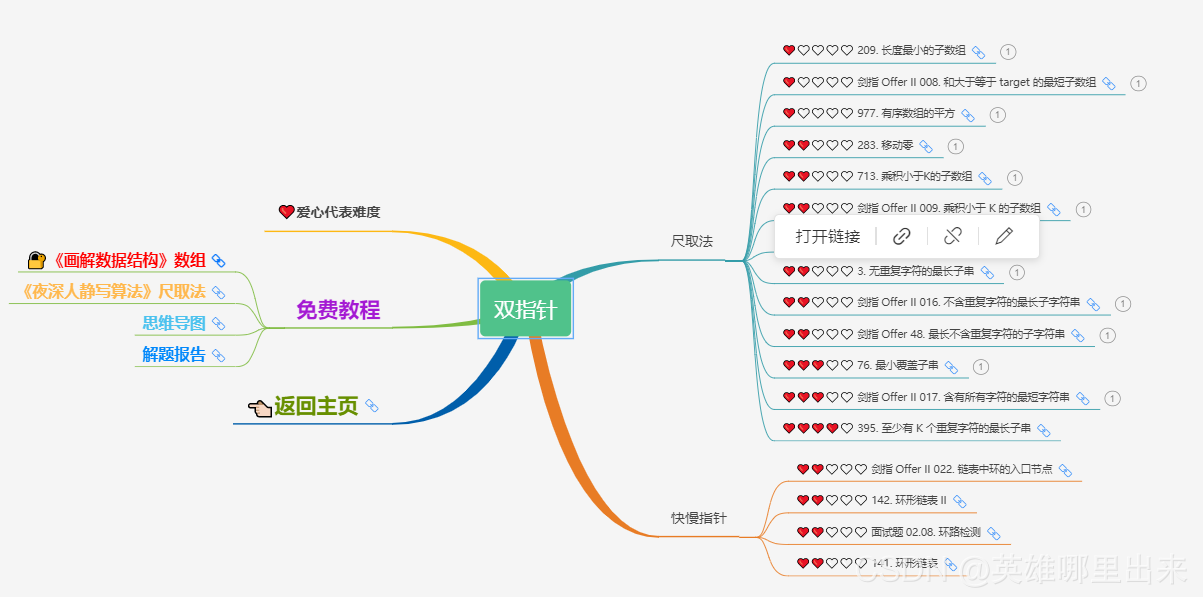
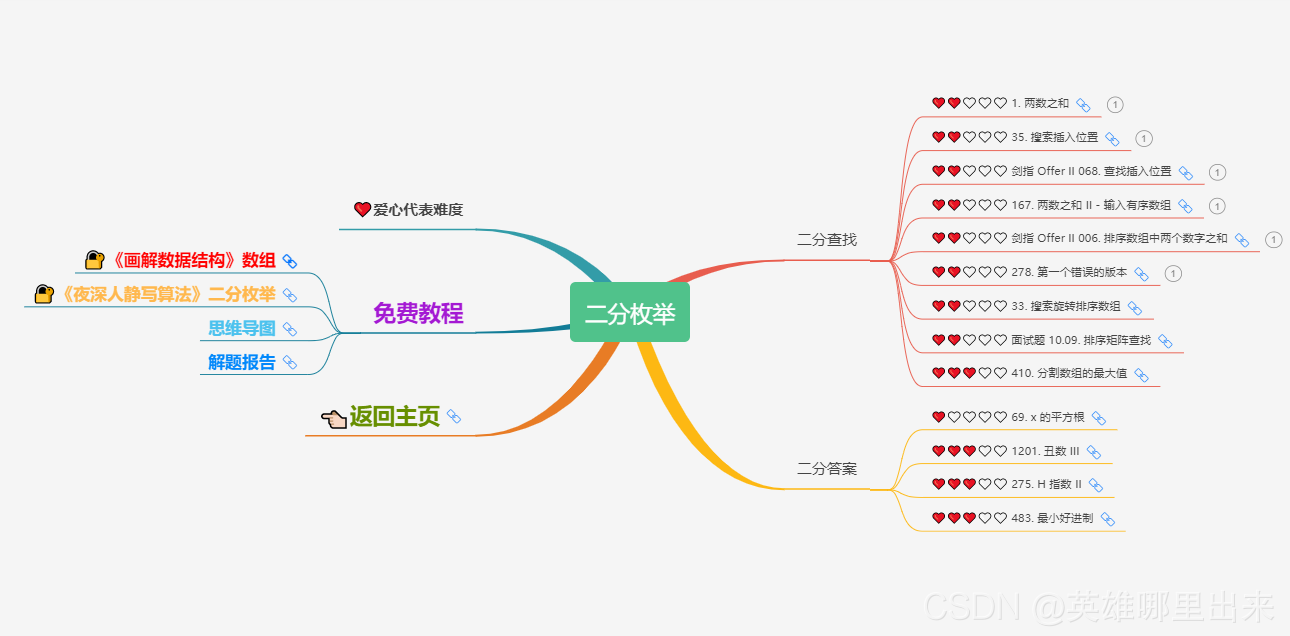


为了让这件事情变得有趣,以及「 照顾初学者 」,目前题目只开放最简单的算法 「 枚举系列 」 (包括:线性枚举、双指针、前缀和、二分枚举、三分枚举),当有 一半成员刷完 「 枚举系列 」 的所有题以后,会开放下个章节,等这套题全部刷完,你还在群里,那么你就会成为「 夜深人静写算法 」专家团 的一员。
不要小看这个专家团,三年之后,你将会是别人 望尘莫及 的存在。如果要加入,可以联系我,考虑到大家都是学生, 没有「 主要经济来源 」,在你成为神的路上,「 不会索取任何 」。
🔥让天下没有难学的算法🔥
C语言免费动漫教程,和我一起打卡! 🌞《光天化日学C语言》🌞
入门级C语言真题汇总 🧡《C语言入门100例》🧡
几张动图学会一种数据结构 🌳《画解数据结构》🌳
组团学习,抱团生长 🌌《算法入门指引》🌌
竞赛选手金典图文教程 💜《夜深人静写算法》💜
七、粉丝专属福利
语言入门:《光天化日学C语言》(示例代码)
语言训练:《C语言入门100例》试用版
数据结构:《画解数据结构》源码
算法入门:《算法入门》指引
算法进阶:《夜深人静写算法》算法模板
