文章目录
- 作业题积累
- 1判断闰年
- 题目
- 答案
- 解析
- 2最大公约数和最小公倍数
- 题目
- 答案
- 解析
- 3分数求和
- 题目
- 答案
- 解析
- 4二分查找
- 题目
- 答案
- 解析
- 5字符串逆序
- 题目
- 答案
- 解析
- 代码逻辑
- 6进制转换
- 题目
- 答案
- 解析
- 7冒泡排序
- 题目
- 答案
- 解析
- 8数组操作
- 题目
- 答案
- 解析
- 9打印二进制奇数偶数位
- 题目
- 答案
- 解析
- 10交换两个变量
- 题目
- 答案
- 解析
- 11统计二进制中1的个数
- 题目
- 答案
- 解析
- 12计算求和
- 题目
- 答案
- 解析
- 13自幂数
- 题目
- 答案
- 解析
- 14字符串逆序
- 题目
- 答案
- 解析
- 15喝汽水问题
- 题目
- 答案
- 解析
- 16程序解释
- 题目
- 答案
- 解析
- 17调整奇偶顺序
- 题目
- 答案
- 解析
- 18杨辉三角
- 题目
- 答案
- 解析
- 19猜凶手
- 题目
- 答案
- 解析
- 20程序解释
- 题目
- 答案
- 解析
- 21猜名次
- 题目
- 答案
- 解析
- 22杨氏矩阵
- 题目
- 答案
- 解析
- 23模拟`qsort`
- 题目
- 答案
- 解析
- 24字符串左旋
- 题目
- 答案
- 解析
- 25检查字符串旋转结果
- 题目
- 答案
- 解析
作业题积累
1判断闰年
题目
判断闰年函数。
答案
int main() {
int i = 0;
int leapyear = 0;
for (i = 1000; i <= 1900; i++) {
if ((i % 400 == 0) || (i % 4 == 0 && i % 100 != 0)) {
printf("%d ", i);
}
}
return 0;
}
int is_leap_year(int year) {
return (((year % 4 == 0) && (year % 100 != 0)) || (year % 400 == 0));
}
解析
闰年分为普通闰年和世纪闰年,其判断方法为:
- 普通闰年:年份是4的倍数,且不是100的倍数。
y%4==0&&y%100!=0 - 世纪闰年:年份是整百数,且必须是400的倍数。
y%400==0
若将万年内,设可整除4年的为 S A S_A SA,可整除100年的为 S B S_B SB,可整除400年的为 S C S_C SC。
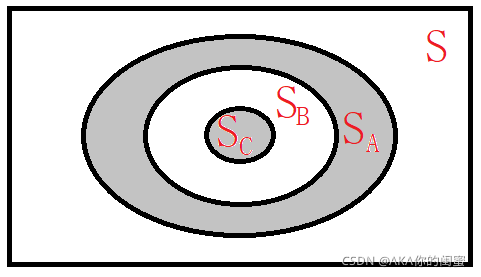
利用这张图,闰年 S S S 可表示为 S A + S C S_A+S_C SA+SC。
四年一闰。百年不闰,四百年再闰。
2最大公约数和最小公倍数
题目
求出最大公因数和最小公倍数。
答案
//1.遍历元素,暴力求解
int main() {
int num1 = 0;
int num2 = 0;
scanf("%d %d", &num1, &num2);
int min = num1 < num2 ? num1 : num2;
int max = num1 < num2 ? num2 : num1;
//遍历元素
for (int i = min; i > 0; i--) {
if (num1 % i == 0 && num2 % i == 0) {
printf("%d", i);
break;
}
}
for(int i = max; i > 0; i++) {
if(i % num1 == 0 && i % num2 == 0) {
printf("%d\n", i);
break;
}
}
return 0;
}
//2.辗转相除法
int main()
{
int a = 0;
int b = 0;
scanf("%d%d", &a, &b);
int tmp = a * b;
int c = 0;
while (c = a % b) {
a = b;
b = c;
}
//最大公约数
printf("%d\n", b);
//最小公倍数
printf("%d\n", tmp / b);
return 0;
}
//1.更相减损法
#include <math.h>
int main()
{
int a = 0;
int b = 0;
scanf("%d %d", &a, &b);
if (a % 2 == 0 && a > 2) {
a /= 2;
}
if (b % 2 == 0 && b > 2) {
b /= 2;
}
if (a < b) {
int tmp = a;
a = b;
b = tmp;
}
int tmp = a - b;
while (b != tmp) {
tmp = abs(tmp - b);
}
printf("%d\n", b);
return 0;
}
解析
- 最小公倍数比二者都大,最大公约数比二者都小。找最小公倍数则从二者中较大的向后遍历,最大公约数是从最小值前前遍历。
- 辗转相除法
- 在二者之模不为0的情况下,除数赋给被除数,模赋给除数,再执行整数除法直至模为0时,除数为最大公约数,初始二者数值乘积除以最大公约数即为最小公倍数。
- 更相减损法
- 若二者能整除2则除,不可的话,那么用大数减去小数,互相减来减去,一直到减数与差相等为止,此时所得即最大公约数。
3分数求和
题目
计算1/1-1/2+1/3-1/4+1/5 …… + 1/99 - 1/100 的值,打印出结果。
答案
int main()
{
int num = 100;
double flg = 1.0;
double sum = 0;
for (int Den = 1; Den <= num; Den++) {
//1.
double pro = flg / (Den / 1.0);//小数能影响除法
//2.
double pro = flg / Den;
sum += pro;
flg = -flg;
}
printf("%lf\n", sum);
return 0;
}
解析
注意只有一个小数参与除法运算才可以触发小数除法。故第二中直接把分子定义为浮点数,通过取负得到±1。
4二分查找
题目
二分查找,在一个有序整型数组中查找某个数字。
答案
int main() {
int arr[10] = { 1,2,3,4,5,6,7,8,9,10 };
int sz = sizeof(arr)/sizeof(arr[0]);
int key = 0;
scanf("%d", &key);
int left = 0;
int right = sz - 1;
while(left <= right) {
int mid = (left + right) / 2;
if (arr[mid] > key) {
right = mid - 1;
}
else if (arr[mid] < key) {
left = mid + 1;
}
else {
printf("找到了下标为%d\n", mid);
}
}
if (left > right) {
printf("找不到\n");
}
return 0;
}
解析
通过下标访问元素进行对比,从中间开始。临界条件是左下标小于右下标。当然折半法仅限有序数组。
5字符串逆序
题目
编写一个函数 reverse(char* str),用递归的方式实现:将参数字符串中的字符反向排列,不是逆序打印。
要求:不能使用C函数库中的字符串操作函数。
例如:char arr[] = "abcdef";,逆序之后数组内容变成:fedcba
答案
void reverse_string3(char* ch)//递归
{
char* left = ch;
char* right = ch + strlen(ch) - 1;
if (*ch != '\0')
{
char tmp = *left;//提取
*left = *right;//赋值
*right = '\0';//赋\0
reverse_string3(ch+1);//ch+1,而不是ch++
*right = tmp;//赋值
}
}
解析
abcdef递推:(先把后面赋值给前面,后面用覆盖\0)
$ \Rightarrow$
f b c d e \0⇒ \Rightarrow ⇒
f e c \0\0⇒ \Rightarrow ⇒
f e d \0\0\0回归:(把前面转移出去的字符对应赋值给\0)
$ \Rightarrow$
f e d c \0\0⇒ \Rightarrow ⇒
f e d c b \0⇒ \Rightarrow ⇒
f e d c b a
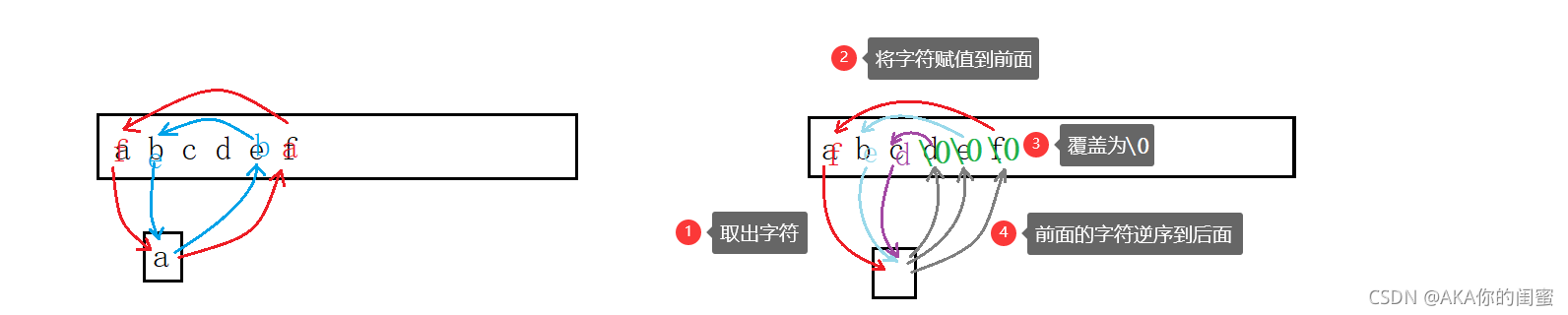
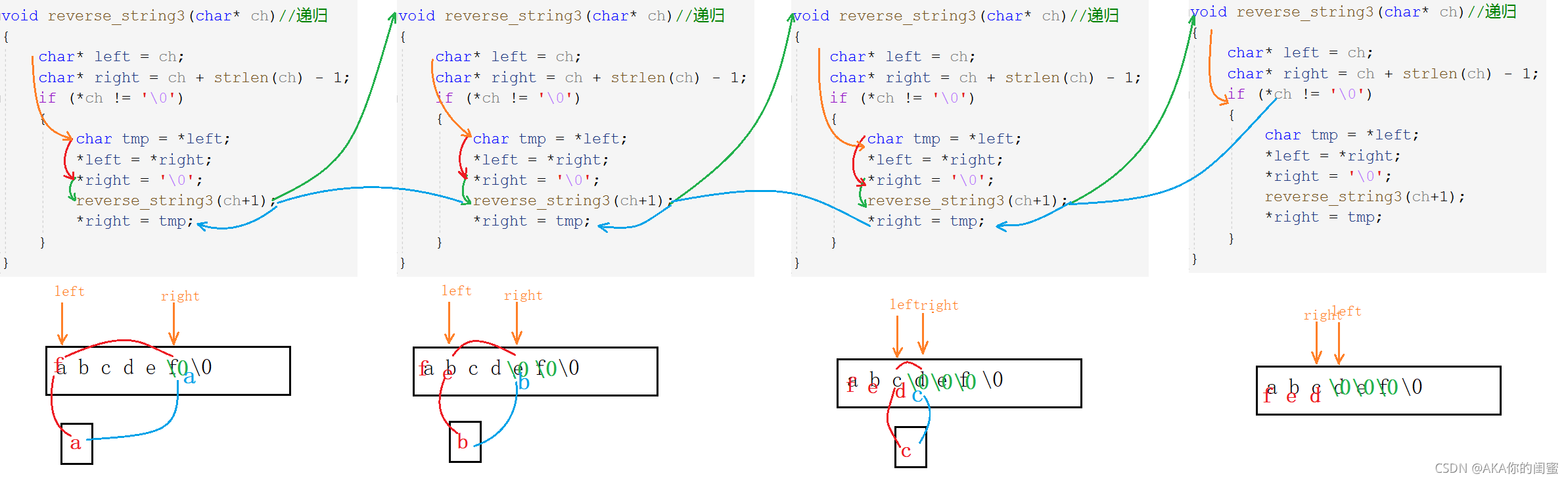
代码逻辑
reverse(“abcdef\0”)
交换a和f+reverse(“f bcde\0\0”)
交换a和f+交换b和e+reverse(“fe cd\0\0\0”)
交换a和f+交换b和e+交换c和d+reverse(“fed \0\0\0\0”)
- 交换两个字符
- 将在前的字符先放到一边存着
- 把在后的字符赋值到前面的位置
- 再把后面的位置对应覆盖为
\0- 原在前字符替换
\0
- 把事先存好的在前的字符对应替换到
\0的位置上
6进制转换
题目
将一个十进制数转换成二进制并打印二进制序列的每一位。
答案
void Bin(n)
{
if (n / 2 != 0)
{
Bin(n / 2);
}
printf("%d", n % 2);
}
解析
10进制数转换成二进制数,这是一个连续除2的过程:
- 把要转换的数,除以2,得到商和余数,
- 将商继续除以2,直到商为0。
最后将所有余数倒序排列,得到数就是转换结果。
7冒泡排序
题目
有一个无序的整型数组,使用冒泡排序的方法使其按升序或降序的方式排序。
答案
int BubbleSort() {
int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
int sz = sizeof(arr) / sizeof(arr[0]);
for (int i = 0; i < sz - 1; i--) {
for (int j = 0; j < sz - 1 - i; j++) {
if (arr[j] < arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
}
解析

冒泡排序的核心思想是相邻两数相比,可以抽象为一个比较函数。
基本思路是比较 n − 1 n-1 n−1 趟,每趟比较 n − 1 − i n-1-i n−1−i 次。
因为外循环结束一次排序完一个数,使其来到其最终位置上,内循环一次使其与未经和其比较的数进行比较,并在满足条件的情况下进行交换,所以每次减
i。
8数组操作
题目
实现reverse()函数完成数组元素的逆置。
答案
void reverse(int arr[], int sz)
{
int left = 0;
int right = sz - 1;
while (left < right)
{
int tmp = arr[left];
arr[left] = arr[right];
arr[right] = tmp;
left++;
right--;
}
}
解析
通过下标访问数组元素从左向右依次进行交换。这种逆序整型数组也可以逆序字符串。都是一样的字符串也可以通过下标访问。
9打印二进制奇数偶数位
题目
输入一个整数,分别打印其二进制序列的奇数位和偶数位。
答案
int main() {
int n = 0;
int i = 0;
scanf("%d", &n);
printf("奇数位:");
for (i = 30; i >= 0; i -= 2) {
printf("%d ", (n >> i) & 1);
}
printf("\n偶数位:");
for (i = 31; i >= 1; i -= 2) {
printf("%d ", (n >> i) & 1);
}
return 0;
}
解析

循环遍历二进制序列中的每一位,让每一位右移上i位都有机会来到最后一位和整数1按位与,这样得到的数也只能1或0,这样就相当于变相得到二进制序列的每一位。由于要区分奇数位和偶数位且按照顺序打印,故要从后往前遍历。
10交换两个变量
题目
不创建临时变量的条件下,交换两个整型变量。
答案
int main()
{
int a = 10;
int b = 20;
printf("a=%d,b=%d\n", a, b);
//1.
a = a + b;
b = a - b;
a = a - b;
//2.
//(a^b)^a=b (a^b)^b=a
a = a ^ b;
b = a ^ b;
a = a ^ b;
printf("a=%d,b=%d\n", a, b);
return 0;
}
解析
不创建临时变量来交换两个整数数据。
- 通过赋值的方法,把
a+b赋值给a,此时a已经等于a+b,再将a-b赋值给b,这样b就等于原来的a,再用a-b,这样就得到了b再赋值给a。这样a,b就完成了交换。 - 通过按位异或的方法,按位异或的特点是,相同为0,相异为1。这样就会导致一个结果
(a^b)^a=b,(a^b)^b=a。这样的话把a^b的结果再与b异或然后赋值给b,再将a^b,也就是(a^b)^a=b赋值给a。
但二者都有局限,前者的大小受限,a+b加起来不可以大于一个整型不然就会溢出。后者因按位操作符仅是由于整型,故后者也受限于变量类型为整型。
11统计二进制中1的个数
题目
输入一个整数,统计其二进制序列中1的个数。
答案
- 方法1
int Return_Number_1(int n)
{
int i = 0;
int count = 0;
for (i = 0; i < 32; i++)
{
if (((n >> i) & 1) == 1)
{
count++;
}
}
return count;
}
int main()
{
int n = 0;
scanf("%d", &n);
printf("%d\n", Return_Number_1(n));
return 0;
}
- 方法2
int main()
{
int n = 0;
int count = 0;
scanf("%d", &n);
while (n) {
n = n & (n - 1);
count++;
}
printf("%d\n", count);
return 0;
}

解析
如图所示我们用n&(n-1)作为计数器的条件,可以发现n&(n-1)的结果比n的二进制序列少一个1,再将结果赋值给n,就可以依靠循环来实现计数器。
12计算求和
题目
求 S n = a + a a + a a a + a a a a + a a a a a Sn = a + aa + aaa + aaaa + aaaaa Sn=a+aa+aaa+aaaa+aaaaa 的前5项之和,其中 a a a 是一个数字,例如: 2 + 22 + 222 + 2222 + 22222 2 + 22 + 222 + 2222 + 22222 2+22+222+2222+22222。
答案
第一种思路:
2 = 2*10^0
22 = 2*10^1 + 2
222 = 2*10^2 + 22
2222 = 2*10^3 + 222
22222 = 2*10^4 + 2222
22222 = 2*10^4 + 2222
第二种思路:
2 = 2 + 0
22 = 2 * 10 + 2
222 = 22 * 10 + 2
2222 = 222 * 10 + 2
22222 = 2222 * 10 + 2
#include <math.h>
int main()
{
int a = 0;
scanf("%d", &a);
int sum = 0;
int ret = 0;
for (int i = 0; i < 5; i++) {
//1.
ret += a * (int)pow(10, i);
//2.
ret = ret * 10 + a;
sum += ret;
}
printf("%d\n", sum);
return 0;
}
第三种方法:
#include <math.h>
int main()
{
int a = 0;
int n = 0;
int sum = 0;
scanf("%d %d", &a, &n);
while (n) {
int i = n;
int ite = 0;
while (i) {
ite += a * pow(10, i - 1);
i--;
}
sum += ite;
n--;
}
printf("%d\n", sum);
return 0;
}
解析
-
第一种是把 a a a 看作 a × 1 0 0 a×10^0 a×100, a a aa aa 看成 a × 1 0 1 + a × 1 0 0 a×10^1+a×10^0 a×101+a×100 ……
-
第二种每次在前一次运算的结果上乘10并加上2。
-
第三种是可以规定位数。
13自幂数
题目
求出0~100000之间的所有“水仙花数”并输出。
“水仙花数”是指一个n位数,其各位数字的n次方之和确好等于该数本身,如:
153
=
1
3
+
5
3
+
3
3
153=1^3+5^3+3^3
153=13+53+33 。
则153是一个“水仙花数”。
答案
#include<math.h>
int main() {
for (int i = 0; i < 10000; i++) {
//1. 求位数
int n = 1;
int num = i;
while (num /= 10) {
n++;
}
//2. 求每项和
int sum = 0;
num = i;
while (num) {
sum += (int)pow((num % 10), n);
num /= 10;
}
//3. 判断
if (sum == i) {
printf("%d\n", i);
}
}
return 0;
}
解析
求自幂数需要三步,1求出该数的位数2求每项和3.判断是否相等。每次做出改变i动作时,要把i赋值给临时变量以免在循环内改变临时变量。
14字符串逆序
题目
现有一字符串i am a student,将其全部逆序得tneduts a ma i。
进阶版:将其单词外逆序,单词内顺序不变,得:student a am i。
答案
#include <string.h>
char* reverse(char* arr) {
int len = strlen(arr);
char* left = arr;
char* right = arr + len - 1;
while (left < right) {
char tmp = *left;
*left = *right;
*right = tmp;
left++;
right--;
}
return arr;
}
int main()
{
char arr[] = "i am a student";
reverse(arr);
printf("%s\n", arr);
return 0;
}
进阶版:
char* reverse(char* left, char* right) {
while (left < right) {
char tmp = *left;
*left = *right;
*right = tmp;
left++;
right--;
}
return left;
}
char* move(char* arr) {
int len = strlen(arr);
reverse(arr, arr + len - 1);
reverse(arr, arr + 6);
reverse(arr + 8, arr + 8);
reverse(arr + 10, arr + 11);
reverse(arr + 13, arr + 13);
return arr;
}
//tneduts a ma i
//01234567890123
int main()
{
char arr[] = "i am a student";
move(arr);
printf("%s\n", arr);
return 0;
}
解析
把所有单词都可视为字符,故逆序字符串即可。进阶版只需要将全部逆序后的结果数清每个字符的下标位置,并单独在逆序就可以了。
15喝汽水问题
题目
喝汽水,1瓶汽水1元,2个空瓶可以换一瓶汽水,给20元,可以多少汽水。
答案
//喝汽水
int main()
{
int money = 20;
//买的
int total = money;
int empty = money;
//换的
while (empty > 1) {
total += empty / 2;
empty = empty / 2 + empty % 2;
}
printf("%d\n", total);
return 0;
}
解析
喝到的汽水可以分为两种,一种是买来的一种是换来的。首先花已有的钱买来的一元一瓶故先total等于money。
然后计算换来的,定义空瓶数,两个空瓶换一瓶,故total等于empty/2,empty执行整数除法,故empty等于不仅要/2还要%2,奇数瓶还会剩下奇数瓶。
16程序解释
题目
请解释下列代码的运行结果和问题原因。
#include <stdio.h>
int main()
{
int i = 0;
int arr[] = { 1,2,3,4,5,6,7,8,9,10 };
for (i = 0; i <= 12; i++)
{
arr[i] = 0;
printf("hello bit\n");
}
return 0;
}
答案

解析
数组其后第三块空间正好被编译器用来放置存储下标的变量,故每次到这里都会清零,就重新开始了。每个编译器的位置不一样,这个属于编译器的自我优化,不是我们可以改变的。且在release版本会优化掉这个问题。
17调整奇偶顺序
题目
调整数组使奇数全部都位于偶数前面。
输入一个整数数组,调整该数组中数字的顺序,使得数组中所有的奇数位于数组的前半部分,所有偶数位于数组的后半部分。
答案
int main()
{
int arr[] = { 1,2,3,4,5,6,7,8,9,10 };
int sz = sizeof(arr) / sizeof(arr[0]);
int* pl = arr;
int* pr = &arr[sz - 1];
while (pl < pr) {
while (*pl % 2 == 1) {
pl++;
}
while (*pr % 2 == 0) {
pr--;
}
if (pl < pr) {
int tmp = *pl;
*pl = *pr;
*pr = tmp;
}
}
for (int i = 0; i < sz; i++) {
printf("%d ", arr[i]);
}
return 0;
}
解析
pl和pr不可以同时加减。在前面用pl寻找奇数,后面用pr寻找偶数。找到之后再两者交换。
18杨辉三角
题目
打印如图所示的数据三角形。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
打印杨辉三角菱形形式。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
答案
int main()
{
int n = 0;
scanf("%d", &n);
int arr[20][20] = { 0 };
arr[1][1] = 1;
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= i; j++) {
arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];//规律
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
printf("%d ", arr[i][j]);
}
printf("\n");
}
}
进阶版:
int main()
{
int arr[10][10] = { 0 };
for (int i = 0; i < 10; i++) {
for (int j = 0; j <= i; j++) {
//初始化
arr[i][0] = arr[i][i] = 1;
//计算
if (i >= 2 && j >= 1) {
arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
}
//打印
printf("%d ", arr[i][j]);
}
printf("\n");
}
for (int i = 0; i < 10; i++) {
for (int j = 0; j < 10; j++) {
if (j < 9 - i) {
printf(" ");
}
else {
printf("%d ", arr[i][j - 9 + i]);
}
}
printf("\n");
}
return 0;
}
解析
首先杨辉三角的规律为 a r r [ i ] [ j ] = a r r [ i − 1 ] [ j − 1 ] + a r r [ i − 1 ] [ j ] arr[i][j] = arr[i-1][j-1]+arr[i-1][j] arr[i][j]=arr[i−1][j−1]+arr[i−1][j] 。
- 第一种初始化时是从第2行第2列初始化,将arr[1][1]置为1。
- 第二种是将第1列和对角线初始化为1,然后从第3行第2列开始初始化。
19猜凶手
题目
日本某地发生了一件谋杀案,警察通过排查确定杀人凶手必为4个嫌疑犯的一个。以下为4个嫌疑犯的供词:
A说:不是我。
B说:是C。
C说:是D。
D说:C在胡说
已知3个人说了真话,1个人说的是假话。
现在请根据这些信息,写一个程序来确定到底谁是凶手。
答案
int main()
{
int kill = 0;
//枚举法,一一列举
for (kill = 'A'; kill <= 'D'; kill++) {
//利用表达式返回值特点,直观
if ((kill != 'A') +
(kill == 'C') +
(kill == 'D') +
(kill != 'D') == 3) {
printf("%c\n", kill);
break;
}
}
return 0;
}
解析
定义killer变量,将是与不是转化为关于killer变量的关系运算。因为只有ABCD每人一个条件故只要一个循环即可。三人真话,一人假话,故所有条件表达式相加的结果应为3,在killer假设条件正确时。
20程序解释
题目
求代码中strlen(a)的结果,并解释清楚原因。
int main()
{
char a[1000] = { 0 };
int i = 0;
for (i = 0; i < 1000; i++)
{
a[i] = -1 - i;
}
printf("%d", strlen(a));
return 0;
}
答案
255
解析
求strlen(a)的值,也就是求a[i]=0的时候,i为多少,准确的来说应该是-1-i等于多少。因为数组a为字符元素数组,故当-1-i的尾七位二进制补码为全1的时候,由于存入数组时发生截断故存入的是0。
21猜名次
题目
5位运动员参加了10米台跳水比赛,有人让他们预测比赛结果:
A选手说:B第二,我第三;
B选手说:我第二,E第四;
C选手说:我第一,D第二;
D选手说:C最后,我第三;
E选手说:我第四,A第一;
比赛结束后,每位选手都说对了一半,请编程确定比赛的名次。
答案
int main()
{
int a = 0;
int b = 0;
int c = 0;
int d = 0;
int e = 0;
for (a = 1; a <= 5; a++) {
for (b = 1; b <= 5; b++) {
for (c = 1; c <= 5; c++) {
for (d = 1; d <= 5; d++) {
for (e = 1; e <= 5; e++) {
//循环5^5次
//判断条件1.
//if ((b == 2) + (a == 3) +
// (b == 2) + (e == 4) +
// (c == 1) + (d == 2) +
// (c == 5) + (d == 3) +
// (e == 4) + (a == 1) == 5) {
//判断条件2.
if (((b == 2) + (a == 3) == 1) &&
((b == 2) + (e == 4) == 1) &&
((c == 1) + (d == 2) == 1) &&
((c == 5) + (d == 3) == 1) &&
((e == 4) + (a == 1) == 1)) {
if (a * b * c * d * e == 120) {//1*2*3*4*5=120
printf("a=%d,b=%d,c=%d,d=%d,e=%d\n", a, b, c, d, e);
goto again;
return 0;
}
}
}
}
}
}
}
again:
}
解析
找凶手的题目凶手只有一个,猜名次必须要排序,所以要有5个循环,每个循环判断一个选手的名次。同样是把所有人的话作为一个条件,限制条件是每个人只有半句是对的,所以是两个条件加起来是1。最后要取出排名重复的情况。
22杨氏矩阵
题目
有一个数字矩阵,矩阵的每行从左到右是递增的,矩阵从上到下是递增的,
请编写程序在这样的矩阵中查找某个数字是否存在。
要求:时间复杂度小于O(N);
答案
void find_key(int(*pa)[3], int* px, int* py, int k) {
int x = *px;
int y = *py;
while (x < 3 && y >= 0) {
if (pa[x][y] > k) {
y--;
}
else if (pa[x][y] < k) {
x++;
}
else {
printf("(%d,%d)\n", x, y);
return;
}
}
printf("NO\n");
}
int main() {
int arr[3][3] = { {1,2,3},{4,5,6},{7,8,9} };
int key = 7;
int x = 0;
int y = 2;
find_key(arr, &x, &y, key);
return 0;
}
解析
因为所谓杨氏矩阵的定义就是该矩阵从左向右递增从上到下递增,不一定是按照某种顺序。同时要求时间复杂度不超过 O ( N = n 2 ) O(N=n^2) O(N=n2),所以不可以遍历,所以从矩阵的特点入手,从矩阵的右上角入手,该数字是该行的最大值,又是该列的最小值。这样就可以通过大小比较来控制行和列。
23模拟qsort
题目
模拟实现my_qsort函数,并排序整型数组。
答案
//打印函数
Print(int* arr, int sz) {
for (int i = 0; i < sz; i++) {
printf("%d ", arr[i]);
}
putchar(10);
}
//比较函数
int cmp(const void* e1, const void* e2) {
return *(int*)e1 - *(int*)e2;
}
//交换函数
void Swap(char* buf1, char* buf2, size_t width) {
for (size_t i = 0; i < width; i++) {
char tmp = *(buf1 + i);
*(buf1 + i) = *(buf2 + i);
*(buf2 + i) = tmp;
}
}
//模拟实现qsort
void my_qsort(void* base, size_t num, size_t width, int(*cmp)(const void*, const void*)) {
for (size_t i = 0; i < num; i++) {
for (size_t j = 0; j < num - i - 1; j++) {
if (cmp((char*)base + j * width, (char*)base + (j + 1) * width) > 0) {
Swap((char*)base + j * width, (char*)base + (j + 1) * width, width);
}
}
}
}
int main() {
int arr[] = { 9,8,7,6,5,4,3,2,1,0 };
int sz = sizeof(arr) / sizeof(arr[0]);
my_qsort(arr, sz, sizeof(arr[0]), cmp);
Print(arr, sz);
return 0;
}
解析
排序函数的要素:起始位置,元素大小,元素宽度以及比较函数。比较函数中要内嵌交换函数。
24字符串左旋
题目
实现一个函数,可以左旋字符串中的k个字符。
例如:ABCD左旋一个字符得到BCDA,ABCD左旋两个字符得到CDAB。
答案
- 第一种方案
#include <string.h>
#include <assert.h>
char* left_hand(char* arr, int k) {
assert(arr);
int len = strlen(arr);
//0. 判断次数
k %= len;
while (k) {
//1. 提取第一个字符
char tmp = arr[0];
//2. 后面的字符向前移动一位
for (int i = 1; i < len; i++) {
arr[i - 1] = arr[i];
}
//3. 插入最后一个字符
arr[len - 1] = tmp;
k--;
}
//4. 返回字符串地址
return arr;
}
int main() {
char arr[] = "ABCD";
int k = 2;
printf("%s\n", left_hand(arr, k));
return 0;
}
- 第二种方案
//AB CDEF
//BA FECD
//CD EFAB
char* reverse(char* left,char* right) {
char* begin = left;
while (left <= right) {
char tmp = *left;
*left = *right;
*right = tmp;
left++;
right--;
}
return begin;
}
char* hand(char* arr, int k) {
int len = strlen(arr);
reverse(arr, arr + k - 1);
reverse(arr + k, arr + len - 1);
reverse(arr, arr + len - 1);
}
int main()
{
char arr[] = "ABCDEF";
int k = 2;
hand(arr, k);
printf("%s\n", arr);
return 0;
}
解析
- 第一种是每次左旋一个字符,再循环k次。左旋的逻辑是提取字符然后剩余元素前移一位最后字符放入最后位置。
- 第二种是确定左旋字符个数后,先分别逆序前后两个字符串,再将整个字符串逆序。
25检查字符串旋转结果
题目
写一个函数,判断一个字符串是否为另外一个字符串旋转之后的字符串。
例如:给定s1 = AABCD和s2 = BCDAA,返回1;给定s1 = ABCD和s2 = ACBD,返回0。
AABCD左旋一个字符得到ABCDA
AABCD左旋两个字符得到BCDAA
AABCD右旋一个字符得到DAABC
答案
- 第一种方案
#include <string.h>
#include <assert.h>
int check_hand(char* s1, char* s2) {
assert(s1 && s2);
int len1 = strlen(s1);
int len2 = strlen(s2);
if (len1 != len2) {
return 0;
}
else {
for (int k = 0; k < len2; k++) {
if (strcmp(left_hand(s1, 1), s2) == 0) {
return 1;
}
}
return 0;
}
}
int main()
{
char s1[] = "AABCD";
char s2[] = "DAABC";
int ret = check_hand(s1, s2);
printf("%d\n", ret);
return 0;
}
- 第二种方案
#include <string.h>
int check_by_add(char* s1, char* s2) {
assert(s1 && s2);
int len = strlen(s1);
char* ps = strncat(s1, s1, len);
if ((size_t)len != strlen(ps)) {
return 0;
}
else {
if (strstr(ps, s1)) {
return 1;
}
else
return 0;
}
}
//AABCD AABCD
int main()
{
char s1[20] = "AABCD";
char s2[20] = "DAABC";
if (check_by_add(s1, s2)) {
printf("Yes\n");
}
else {
printf("No\n");
}
return 0;
}
解析
-
第一种是将需判断字符串与源字符串所有旋转的结果进行比较,同样右旋k个字符也就等于左旋n-k个字符。
-
第二种是字符串最后追加一个源字符串,这样任意旋转后的结果字符串必然是该字符串的子字符串。