本鼠鼠在大三下学期的信息内容安全课程设计报告，我的选题是使用聚类算法实现网页聚类
希望对你的课设或者项目有帮助

---

一、选题内容

该题目给出一组网页地址，然后对指定的网页按内容聚成3类。
网页地址如下：

步骤：
1.抓取指定网址的源码；
2.解析网页文章内容；
3.对文章内容进行分词，并转换成向量表示；(可以考虑用词袋法或TF.IDF。)
4.选取合适的距离公式和聚类算法进行聚类，要求聚成3类。(可以用欧式距离或余弦距离等。聚类方法可以考虑用K-means方法等。)
要求：
1.显示解析后网页文章的内容；(步骤2)
2.显示文章对应的向量；(步骤3)
3.显示文章向量与三个类的类中心的距离。(步骤4)
4.显示最终的分类结果，即哪些网址分为一类。(步骤4)
3、4结果展示可以如下表所示：

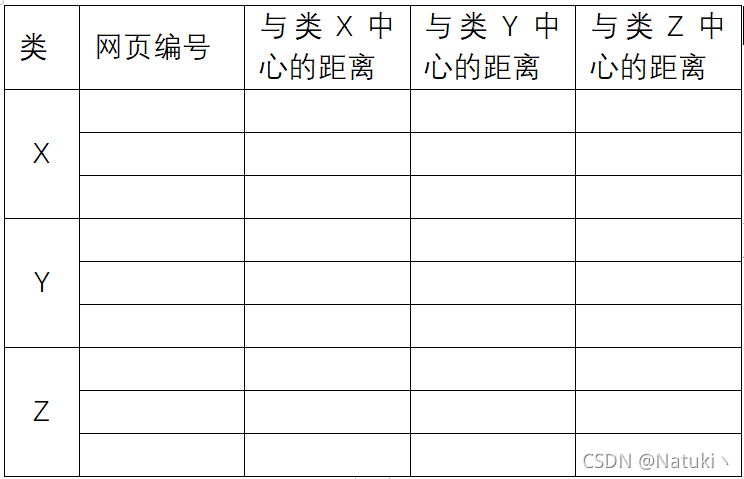
二、方案设计内容

选题：网页聚类系统的设计与实现

任务要求：
（1）显示解析后网页文章的内容；
（2）显示文章对应的向量；
（3）显示文章向量与三个类的类中心的距离。
（4）显示最终的分类结果，即哪些网址分为一类。

2.1、解析网站

读取指定若干网页的url并解析出其源码以及网页内容。

2.2、过滤停用词

其中网页内容中有许多诸如停用词之类的噪声信息，不利于我们对关键信息的把控，所以要通过一个停用词词库来过滤掉这些通用词。

2.3、分词处理

根据现有的词库字典对过滤掉停用词的网页文本内容进行分词处理。

2.4、权重值及向量化表示

每个网页将分词后的词组数据转化成字符串数组储存起来，通过计算每个网页词组数据的权重值TF.IDF并将其结果转化成向量化表示显示。选用余弦距离公式计算不同网页权重值的多维向量。

2.5、聚类初始化处理

选用K-means算法作为聚类算法，思路如下：任选一个对象作为第一个聚类的中心，计算和第一个中心最远的对象作为第二个中心,分别计算剩下的对象与第一个和第二个对象的距离，设D1是该对象距离第一个中心的距离，D2是该对象距离第二个中心的距离，从中取Max（Min（D1，D2）），即剩下的对象中距离两个聚类两个中心距离较小值中的最大值，该最大值所在的对象作为第三个中心。

2.6、聚类实施过程

分配各个数据对象到最近的簇中，重新计算各个聚类的中心，即该簇成员中向量和的平均值，若中心收敛则输出结果，否则将重新分配各个簇的中心重复上述步骤，直到簇的中心收敛，即中心位置不变的时候输出最终聚类的结果。

三、流程图设计

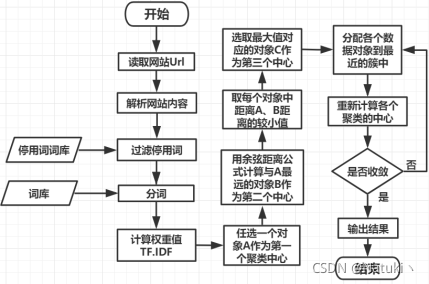
四、系统实现

本系统程序采用C#语言，运行环境为Windows10，编译环境为Microsoft Visual C#

4.1解析网站内容

解析网页内容时使用的是HTMLAgilityPack(1.11.34)，在对网站解析的时候，由于网站格式的不同，解析网站的方法也不同。
一般来说，URL只能使用英文字母、阿拉伯数字和某些标点符号，不能使用其他文字和符号，这是因为网络标准RFC 1738做了硬性规定。这意味着，如果网站内容中有汉字，就必须编码后使用，常见的中文编码有UTF-8、GB2313编码。GBK通常指GB2312编码 只支持简体中文字，utf通常指UTF-8，支持简体中文字、繁体中文字、英文、日文、韩文等语言，支持文字更广。使用HTMLAgilityPack包时要先通过预先设置好的编码方式对网站内容进行对应的解析，不同的编码方式并不互相兼容，出现乱码则意味着编码方式不正确。

4.2、过滤停用词

通过使用字典树Trie实现，字典树是一种树形结构，是哈希树的变种。它的设计和实现是比较简单的，一般来说字典树的典型应用是统计以及排序较多的的字符串，还包括对文本词频的统计。它的优点是：最大限度地减少低效的重复的字符串比较。字典树的根节点不包含字符，而除根节点外每一个节点都只包含一个字符， 从根节点到某一叶子节点，路径上经过的字符连接起来，为该节点对应的字符串， 每个节点的所有子节点包含的字符都不相同。其示意图如下：

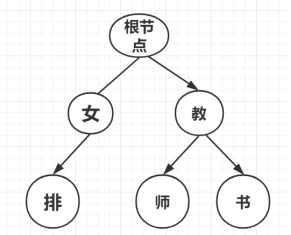
通过已有的停用词库建立一个停用词库字典树，对解析出来的网站内容进行匹配并过滤，该过滤停用词库操作的主要目的是为了除去文本中无关紧要的干扰信息和噪音信息，让有价值的信息更受关注，从而在提高聚类结果的准确性的同时较大程度地降低了计算的资源消耗。

4.3分词处理

在对解析出来的网页内容过滤后需要对该内容进行进一步地分词处理，通过已有的庞大的大概包含2万多条词语的词库字典建立一个字典树，字典在生成trie树的同时, 也把每个词的出现次数转换为了频率。根据给定的词典数进行查词匹配操作, 生成几种可能的句子切分。从句子中某个词的开始位置,到该句子的结尾，每个开始位置作为字典的键, 其中保存了可能的词语的结束位置，通过匹配字典得到词, 开始位置加上词语的长度便得到结束位置。基于前缀词典数可以实现高效的词图扫描，将生成句子中汉字所有可能成词情况所构成的有向无环图(DAG)如下图所示：

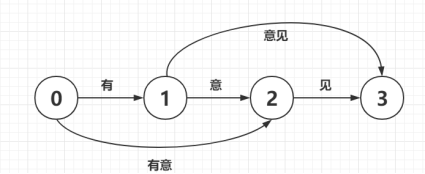
其次，采用了动态规划查找最大概率路径，找出基于词频的最大切分组合查找待分词句子中已经切分好的词语, 对该词语查找该词语出现的频率，即次数除以总数, 如果字典中没有该词就把词典中出现频率最小的那个词语的频率作为该词的频率,根据动态规划查找最大概率路径的方法, 对句子从右往左反向计算最大概率，类似于逆向最大匹配，最后得到最大概率路径对应的切分组合.

4.4、权重值及向量化表示

本程序使用的权重算法是TF.IDF，下面详细介绍它的具体内容。

4.4.1、特征项频率TF（TermFrequeney）

特征项频率是指特征项在文档中出现的次数。特征项可以是字、词、短语，也可以是经过语义概念词典进行语义归并或概念特征提取后的语义单元。不同类别的文档，在某些特征项的出现频率上有很大差异，因此频率信息是文本分类的重要参考之一。在最初的文本自动分类中，文档向量就是用来构造的。

4.4.2、倒排文档频率IDF（InverseDocumentFrequency）

只使用TF会导致两种问题：
（1）文档中大量出现一些对分类没有贡献的虚词如：感叹词、介词、连词等，如果这些词出现的频率过大，在特征提取的时候将这些词选做了特征词条，而对分类产生负面的影响。
（2）特征词的好坏是看能否代表类和文档的属性，TF值高的特征词，如果在所有的文档中值都高，那就很难说这样的特征词到底代表哪个文档。因此单纯使用是有很大的局限性的，人们往往将反文档频率和结合使用。
倒排文档频率是特征项在文档集分布情况的量化，其公式如下：

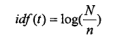
其中为文档集中的总文档数，为出现特征项的文档数。
IDF算法的核心思想是，在大多数文档中都出现的特征项不如只在小部分文档中出现的特征项重要。算法能够弱化一些在大多数文档中都出现的高频特征项的重要度，同时增强一些在小部分文档中出现的低频特征项的重要性。一个有效的分类特征项应该既能体现所属类别的内容，又能将该类别同其他类别相区分。所以，在实际应用中与通常是联合使用的，与的联合公式如公式所示，其中代表类别号：

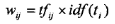
TF.IDF公式有许多变种形式，考虑文本长度对特征权值的影响以及防止聚类过程中个别权值很高的项对其他项的抑制作用，在计算各项权重的时候，应对特征项的权值作归一化处理和适当的均衡处理。本程序采用的是对特征项权值进行均衡处理的公式，如下：

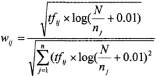
该算法的主要思想是：如果某个词或短语，在一个文档中出现的频率高，并且在其他文档中很少出现，则认为此词或者短语具有很好的类别区分能力，适合用来进行分类；的主要思想是：如果包含词条的文档越少，也就是越小，越大，说明词条具有很好的类别区分能力。

4.5、K-Means算法简介

K-Means算法是一种典型的基于划分的聚类分析算法，算法简单、收敛速度快，被广泛地应用于各个领域。虽然算法具有较强的局部搜索能力，但因对初始聚类中心敏感，容易陷入局部最优，从而影响聚类结果。其基本思想是：根据聚簇数，随机选取个点作为初始聚类中心，依据每个点与初始聚类中心的距离，将所有点划分到个簇中，以每个簇的质心作为新的聚类中心，不断地迭代以上的步骤，对簇进行调整，使簇内对象之间的距离尽可能小，而簇间对象之间的距离尽可能大，直至目标函数收敛。

4.5.1 K-Means算法优点

K-Means算法不依赖于顺序，即一旦给定一个初始中心分布，无论样本点的顺序如何，生成的聚簇都一样。对于算法来说，当结果簇是密集的，而簇类与簇类之间区别明显时，它的聚类效果较好，而且其聚类速度较快。

4.5.2 K-Means算法缺点

（1）初聚类个数k的初始化
K-Means算法的聚类结果依赖于初始值的设定，需要用户事先给出簇的个数，这样一旦用户对待聚类的数据集不了解时，是很难给出合适的值的，很可能会将原本属于同类的对象强行拆分到不同簇中，或者原本不属于一类的对象却被强行合并至一个簇中。
（2）初始聚类中心的选择
K-Means算法的结果依赖于由初始聚类中心出发所遇到的第一个局部极值点，不同的初始聚类中心很可能导致截然不同的聚类结果。一旦初值选择不好，可能无法得到有效的聚类结果，这样的依赖性就导致聚类结果的不稳定性，且容易陷入局部最优而非全局最优。

4.6、对K-Means算法初始化的改进

本课设预先给定了聚类个数k=3，所以我着重考虑了初始中心选择的设计方法。在聚类算法中，初始化是很重要的一个步骤，初始设置的合理性很大程度上直接关系到结果的准确性，如果初始设置不合理，很可能让计算程序陷入局部最优的情况。本程序初始化采用最大最小距离聚类算法，它是模式识别领域中一种比较简单的聚类分析方法。最大最小原则依据待聚类对象的相似情况选择距离尽可能远的对象作为初始聚点最大最小距离聚类算法见算法。
最大最小距离聚类算法的具体实现过程如下：
1）建立网页数据对象集Sn
2）任取其中一个网页对象作为第一个初始化聚类中心Z1
3）计算所有其他网页数据对象到Z1 的距离，取其中中距离最大的值所在的网页数据对象作为第二个初始化聚类中心Z2
4）计算剩下所有网页数据对象到Z1 和Z2的距离，选取剩下的网页数据对象到Z1 、Z2较小值并组合成一个集合，从该集合中找出最大值对应的网页数据对象作为第三个初始化剧烈中心Z3

4.7、K-Means聚类实施过程

4.7.1相似度计算公式的选取

选取的相似度公式是余弦相似度公式，即两向量夹角的余弦作为相似度度量，主要特征是相似度计算不依赖于向量的幅值，公式如下：

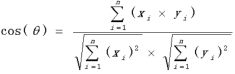
4.7.2余弦相似度公式的优点

他的优点在于其对高维数据中空值的合理性处理，而在高维空间中的某些属性上出现的空值是很普遍的现象。如本文面向的文本数据，每篇文本可以用词频向量表示，由于词表中的词可能很多，而每篇文本一般只包含其中有限的一部分词，这样在代表其他未包含的词的维上就为空，为了向量的比较方便，我们往往给这些空值置0。在使用余弦公式度量时，只是在两个向量中都有值的维才对相似度有贡献，而其中一个向量为空或者两者都为空的维，经过点乘以后都变成了0。

4.7.3聚类过程

1）在初始化完三个聚类中心后，比较每组网页对象数据与该中心的距离，将最近的对象数据添加到对应聚类中心的成员变量中。
2）更新当前聚类中心的数据向量的均值。计算聚类中心均值的方法是：将该簇成员的数据向量累加并除以成员的个数
3）重新计算每个网页数据对象到三个中心的平均值的距离，若网页距离最近的中心对象发生变化则更新对应中心的成员变量
4）若更新完各聚类中心的成员变量后结果没有发生变化，则认为结果是收敛的，输出聚类结果，否则继续执行过程2，直至收敛为止

4.8显示聚类结果

按题目要求，显示的结果需要进行表格化显示，本程序采用C#WPF实现，具有良好的人机交互UI界面。表格信息的内容包括：聚类中心X、Y、Z对应的网页编号以及网页分别与三个中心的距离。
由于上述采用的是相似度计算公式，所以实际意义上的距离是与相似度成反比的，而余弦距离公式的结果区间在[0.1]。其中0表示两个数据对象完全不同，1表示两个数据对象完全相同。所以我们在输出显示距离的时候用1减去相似度值，就可以实现实际意义上距离指标的度量，0代表完全一致，1代表距离无限大。

五、程序演示

程序主界面如图所示：

包含了四个功能：
1）显示解析后网站文章的内容
本程序默认网址页数是9，其中url数据的默认值是题目要求的九个网站，通过HTMLAgilityPack包抓取指定的9个网址后显示网址内容，程序运行结果如下图所示：

2）显示文章对应的向量
通过改进后的公式计算每个网址的TF.iDF值后将其结果向量化输出显示：

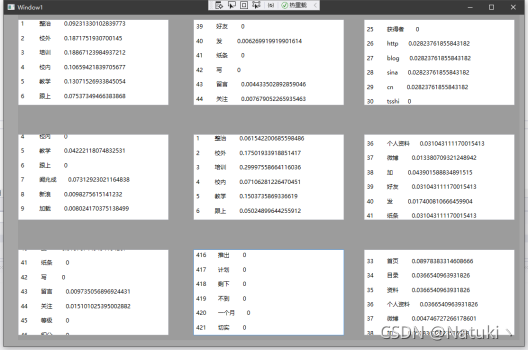
首先在建立每个网址的词组数组数据后，创建一个包含所有网址的词组数组的数据，并以该词组数据为单位每行依次显示本网站对应词组的权重值。
3）以表格形式输出聚类结果
按照题目要求的显示界面，本程序以类似表格输出的形式展示，其中每个中心所在的网页编号以及各自与X、Y、Z中心的距离如图所示，为了方便了解具体分类的情况，在聚类结束后，将距离每个中心最近的网页的前五个最高的权重值所在的词语作为关键词显示出来，如图所示：

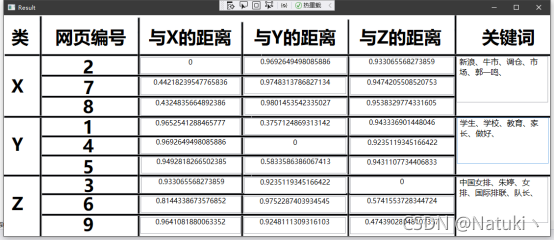
4）重置网页数据
若想重置网页数据可以手动输入或者点击“重置网页”按钮从文本文档txt中读取，默认的读取路径是程序Debug目录下的web.txt文档，这一设置的主要目的是为了避免手动输入9个网址，提高了便利。
在尝试题目要求的九个网站后，我还尝试了其他九个网站，其网站url保存在本地txt文档中方便读取，经验证，结果是准确的

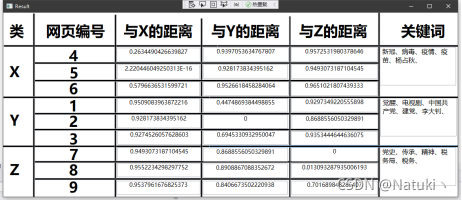
六、分析总结

6.1、比较不同距离算法

本次课设实现的是网页聚类程序，其中聚类算法选择的是K-Means，相似度计算选择的是余弦距离公式，文档权重值选用的是改进后的TF.IDF，在后续的实施过程中，曾尝试过欧氏距离算发，由于在欧式距离算法中每个坐标对欧氏距离的贡献是同等的，通过断点调试发现计算结果带有较大波动区间，并且结果不准确，随后放弃该算法，采用余弦距离公式。
以下是采用欧式距离得出的结果：

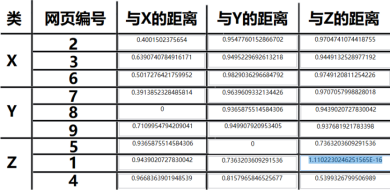
以下是采用余弦距离得出的结果：

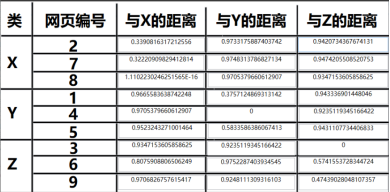
6.2、比较不同的权重距离公式

此外，改进后的TF.iDF算法是为了考虑文本长度对特征权值的影响以及防止聚类过程中个别权值很高的项对其他项的抑制作用。
以下是选用传统的TF*IDF作为权重值的结果，传统算法如下：

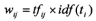
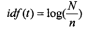
输出结果：

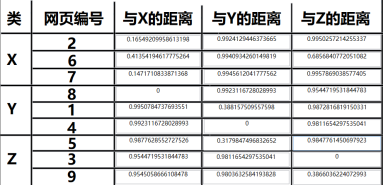
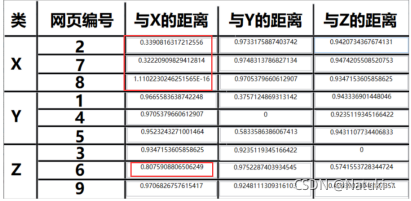
以下是选用改进的TF.IDF作为权重值的结果,改进算法如下：

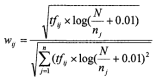
输出结果：

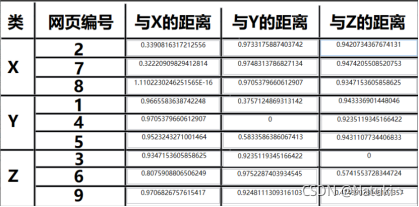
可以明显的看到使用传统距离公式的结果并不准确，并且每簇数据中距离也有不合理的地方，以计算与X的距离为例，该算法结果显示距离X较近的点有四个，并且距离最近的点没有在该聚类中，通过断点调试发现，出现该问题的原因是个别文本长度与其他文本长度差距较大，并且它对特征权值的值波动较大，从而造成聚类过程中该项对其他项产生抑制作用。
其次，由于聚类结果是收敛即输出，由于该算法对权重把控的不准确性导致个别错误数据也跟着收敛了。

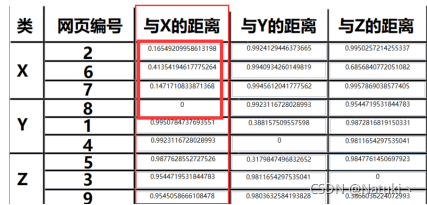
而使用改进后的算法可以看到即使网页6与中心X的距离相比于其他不是同类的网站来说更近但是没有影响到真正距离近的网站，也就是距离是0.8而不是0.9，而传统算法中网页6距离中心X的距离是0.4，可以明显地看到改进后算法的优势。

6.3、比较不同的初始化方法

在上文中已经提到了初始化的重要性，好的初始化中心设置是计算成功的一半，聚类的一大基本原则是中心簇中的数据尽可能接近，而不同中心簇的数据尽可能不同，因此初始化时需要选择最远的三个中心，本文的初始化算法采用最大最小距离算法。并对随机初始化中心和使用该算法做了比较，结果表明，使用了最大最小距离算法后结果的准确性大大提高。

6.4、分析不足之处及改进建议

6.4.1距离算法尝试较少

本次实现虽然对不同的距离算法和权重计算方式产生了比较，但是也是由于最初使用的方法并不理想才选择换一种距离算法的，还有许多诸如绝对值距离法、切比雪夫距离法以及Nsim距离法没有考虑。

6.4.2没有尝试其他聚类算法

由于在设计K-Means算法之后就产生了正确的结果，所以只实现了K-Means算法没有考虑其他方式，此外据查阅资料发现聚类算法除了本文使用的基于划分的K-Means算法外常用的聚类算法还有基于层次的聚类算法、基于密度的方法以及基于模型的聚类算法。可以改进的地方是多尝试其他算法并比较哪一个算法更适合网页聚类。

6.4.3没有考虑网页标签的权重

其次，在考虑计算权重时，只是计算TF以及IDF对应的值并进行相应的改进，没有考虑到网页是半结构化的，每一个网页内容都有相应的标签，每个标签的权重值应该是不一样的，比如标题内容的权重值应该比正文内容的权重值大等。这一思想事先考虑到了但是没有距离落实。

6.4.4输出UI界面的兼容性差

最后，根据题目的要求，本程序的UI界面是针对9个网页3个聚类中心而设计的，虽然不同个数的网页在算法执行后是没有问题的，是能够计算出聚类结果的，但是由于输出只能是9个网页3个中心，后续没有进一步优化界面达到兼容不同个数网页以及不同个数的聚类中心，尚可改进。

七、关键代码展示

主程序段

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.IO;
using System.Linq;
using System.Net;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
using HtmlAgilityPack;
using JiebaNet.Analyser;
using JiebaNet.Segmenter;
using HtmlDocument = HtmlAgilityPack.HtmlDocument;
namespace K_means_Web_Cluster
{
    public partial class Form1 : Form
    {
        private string[] urls =
            {
            "http://blog.sina.com.cn/s/blog_59d698c90102zfct.html",
            "http://blog.sina.com.cn/s/blog_9c2fe26f0102z3ja.html?tj=fina",
            "http://blog.sina.com.cn/s/blog_6479dc5b0102ymb3.html",
            "http://blog.sina.com.cn/s/blog_59d698c90102zfd2.html",
            "http://blog.sina.com.cn/s/blog_59d698c90102zfcl.html",
            "http://blog.sina.com.cn/s/blog_14fdd56530102yknf.html?tj=tiyu",
            "http://blog.sina.com.cn/s/blog_62dc4e590102zot3.html?tj=fina",
            "http://blog.sina.com.cn/s/blog_1506181220102z9x9.html?tj=fina",
            "http://blog.sina.com.cn/s/blog_683c082b0102z3qc.html"
             };
        private Trie StopTree = new Trie();
        private string[] A1;
        private double[] IDFs;
        private  Web[]Webs;
        private string[] ALLterms;
        private string[][] _2Ddocs;
        private string[][] _2Dterms;
        public Form1()
        {
            InitializeComponent();
        }
        public void InitializeWebs()
        {
            _2Ddocs = new string[9][];
            _2Dterms = new string[9][];
            List<string> AllArr = new List<string> { };
            StopTree.initialize();
            Webs = new Web[9];
            var web = new HtmlWeb();
            web.OverrideEncoding = Encoding.GetEncoding("utf-8");
            int LL = 0;
            for (int i = 0; i < 9; i++)
            {
                var doc = web.Load(urls[i]);
                var node = doc.DocumentNode;
                var segmenter = new JiebaSegmenter();
                var segments = segmenter.Cut(node.InnerText);
                string[] ids = segments.ToArray();
                ids = DelectStr(ids);
                _2Ddocs[i] = ids;
                _2Dterms[i] = GetDistinctWords(_2Ddocs[i]);
                LL = _2Dterms[i].Length;
                for (int k = 0; k < LL; k++)
                {
                    if (!AllArr.Contains(_2Dterms[i][k]))
                    {
                        AllArr.Add(_2Dterms[i][k]);
                    }
                }
            }
            ALLterms = AllArr.ToArray();
            for (int i = 0; i < 9; i++)
            {
                Webs[i] = new Web(_2Ddocs[i], ALLterms);
            }
            int AllTermsLen = ALLterms.Length;
            IDFs = new double[AllTermsLen];
            int tt = 0;
            for (int i = 0; i < AllTermsLen; i++)
            {
                for (int k = 0; k < 9; k++)
                {
                    tt += Webs[k].IsContain(ALLterms[i]);
                }
                IDFs[i] = Math.Log10(0.01 + ((double)9 / (double)(tt)));
                tt = 0;
            }
            for (int i = 0; i < 9; i++)
            {
                double aa = 0;
                Webs[i].iTFIDFs = new double[AllTermsLen];
                for (int k = 0; k < AllTermsLen; k++)
                {
                    aa += Webs[i].iTFs[k] * IDFs[k] * IDFs[k];
                }
                for (int k = 0; k < AllTermsLen; k++)
                {
                    Webs[i].iTFIDFs[k] = Math.Sqrt
                        (Webs[i].iTFs[k] * IDFs[k] / aa);
                }
            }
        }
        private void button1_Click(object sender, EventArgs e)
        {
            string url = urls[1];
            Encoding enc = Encoding.GetEncoding("utf-8");
            WebClient webClient = new WebClient();
            webClient.Credentials = CredentialCache.DefaultCredentials;
            byte[] pagedata = webClient.DownloadData(url);
            string pagehtml = enc.GetString(pagedata);
            richTextBox1.AppendText(pagehtml);
            var web = new HtmlWeb();
            web.OverrideEncoding = Encoding.GetEncoding("utf-8");
            var doc = web.Load(url);
            HtmlNode node = doc.DocumentNode;
            richTextBox2.AppendText(node.InnerText);
        }

        private void button2_Click(object sender, EventArgs e)
        {
            StopTree.initialize();
            var segmenter = new JiebaSegmenter();
            var segments = segmenter.Cut(richTextBox2.Text);
            richTextBox1.Clear();     
            string[] ids = segments.ToArray();          
            ids = DelectStr(ids);
            A1 = ids;
            for (int i = 0; i < ids.Length; i++)
            {
                richTextBox1.AppendText(ids[i] + '\n');
            }
        }
        public string[] DelectStr(string[] str)
        {
            List<string> Arr = new List<string> { };
            for (int i = 0; i < str.Length; i++)
            {
                if (str[i] == "\n" || str[i] == "" ||
                    str[i] == " " || str[i] ==" " || str[i] == "\r\n" || StopTree.Contains(str[i]) || str[i] == "\t")
                {
                    ;
                }
                else
                {
                    Arr.Add(str[i]);
                }
            }
            return Arr.ToArray();
        }
        private void button3_Click(object sender, EventArgs e)
        {
            InitializeWebs();
            WawaKMeans kmeans = new WawaKMeans(Webs, 3);
            kmeans.Start();
            WawaCluster[] clusters = kmeans.Clusters;
            foreach (WawaCluster cluster in clusters)
            {
                List<int> members = cluster.CurrentMembership;
                richTextBox3.AppendText('\n'+"-----------------"+'\n');
                foreach (int i in members)
                {
                    richTextBox3.AppendText(i.ToString());
                }
            }
        }
        public static string[] GetDistinctWords(String[] input)
        {
            if (input == null)
                return new string[0];
            else
            {
                List<string> list = new List<string>();

                for (int i = 0; i < input.Length; i++)
                    if (!list.Contains(input[i])) // N-GRAM SIMILARITY?				
                        list.Add(input[i]);

                return list.ToArray();
            }
        }
        public double ComWebDistance(Web X,Web Y)
        {
            double[] x = X.iTFIDFs;
            double[] y = Y.iTFIDFs;
            int len = x.Length;
            double dis=0;
            for(int i=0;i<len;i++)
            {
                dis += (
                    (double)(1)) / 
                    ((double)(1 + Math.Abs(x[i] - y[i]))
                    );
            }
            dis /= len;
            return dis;
        }
    }
}

K-Means实现

using System;

namespace K_means_Web_Cluster
{

    public class WawaKMeans
    {
        /// <summary>
        /// 数据的数量
        /// </summary>
        readonly int _webCount;
        /// <summary>
        /// 原始数据
        /// </summary>
        readonly Web[] _webs;
        /// <summary>
        /// 聚类的数量
        /// </summary>
        readonly int _k;
        /// <summary>
        /// 聚类
        /// </summary>
        double[,] WebDistanceCache;
         /// <summary>
         /// 网页距离缓存
         /// </summary>
        private readonly WawaCluster[] _clusters;

        internal WawaCluster[] Clusters
        {
            get { return _clusters; }
        }

        /// <summary>
        /// 定义一个变量用于记录和跟踪每个资料点属于哪个群聚类
        /// _clusterAssignments[j]=i;// 表示第 j 个资料点对象属于第 i 个群聚类
        /// </summary>
        readonly int[] _clusterAssignments;
        /// <summary>
        /// 定义一个变量用于记录和跟踪每个资料点离聚类最近
        /// </summary>
        private readonly int[] _nearestCluster;
        /// <summary>
        /// 定义一个变量，来表示资料点到中心点的距离,
        /// 其中—_distanceCache[i][j]表示第i个资料点到第j个群聚对象中心点的距离；
        /// </summary>
        private readonly double[,] _distanceCache;


        public WawaKMeans(Web[]webs, int K)
        {
            _webs = webs;
            _webCount = webs.Length;
            _k = K;
            _clusters = new WawaCluster[K];
            _clusterAssignments = new int[_webCount];
            _nearestCluster = new int[_webCount];
            _distanceCache = new double[_webCount, _k];
            InitRandom();
        }

        public void Start()
        {
            while (true)
            {
                //1、重新计算每个聚类的均值
                for (int i = 0; i < _k; i++)
                {
                    _clusters[i].UpdateMean(_webs);
                }

                //2、计算每个数据和每个聚类中心的距离
                for (int i = 0; i < _webCount; i++)
                {
                    for (int j = 0; j < _k; j++)
                    {
                        double dist = ((double)(1))/(getCosDistance(_webs[i], _clusters[j].Mean));
                        _distanceCache[i, j] = dist;
                    }
                }

                //3、计算每个数据离哪个聚类最近
                for (int i = 0; i < _webCount; i++)
                {
                    _nearestCluster[i] = nearestCluster(i);
                }

                //4、比较每个数据最近的聚类是否就是它所属的聚类
                //如果全相等表示所有的点已经是最佳距离了，直接返回；
                int k = 0;
                for (int i = 0; i < _webCount; i++)
                {
                    if (_nearestCluster[i] == _clusterAssignments[i])
                        k++;

                }
                if (k == _webCount)
                    break;

                //5、否则需要重新调整资料点和群聚类的关系，调整完毕后再重新开始循环；
                //需要修改每个聚类的成员和表示某个数据属于哪个聚类的变量
                for (int j = 0; j < _k; j++)
                {
                    _clusters[j].CurrentMembership.Clear();
                }
                for (int i = 0; i < _webCount; i++)
                {
                    _clusters[_nearestCluster[i]].CurrentMembership.Add(i);
                    _clusterAssignments[i] = _nearestCluster[i];
                }
            }

        }

        /// <summary>
        /// 计算某个数据离哪个聚类最近
        /// </summary>
        /// <param name="ndx"></param>
        /// <returns></returns>
        int nearestCluster(int ndx)
        {
            int nearest = -1;
            double min = Double.MaxValue;
            for (int c = 0; c < _k; c++)
            {
                double d = _distanceCache[ndx, c];
                if (d < min)
                {
                    min = d;
                    nearest = c;
                }

            }
            if (nearest == -1)
            {
                ;
            }
            return nearest;
        }
        /// <summary>
        /// 计算某数据离某聚类中心的距离
        /// </summary>
        /// <param name="coord"></param>
        /// <param name="center"></param>
        /// <returns></returns>
        static double getDistance(Web coord, double[] center)
        {
            double[] x = coord.iTFIDFs;
            double[] y = center;
            int len = x.Length;
            double dis = 0;
            for (int i = 0; i < len; i++)
            {
                dis += (
                    (double)(1)) /
                    ((double)(1 + Math.Abs(x[i] - y[i]))
                    );
            }
            dis /= len;
            return dis;
        }
        /// <summary>
        /// 随机初始化k个聚类
        /// </summary>
        /// 
        static public double ComWebDistance(Web X, Web Y)
        {
            double[] x = X.iTFIDFs;
            double[] y = Y.iTFIDFs;
            int len = x.Length;
            double dis = 0;
            for (int i = 0; i < len; i++)
            {
                dis += (
                    (double)(1)) /
                    ((double)(1 + Math.Abs(x[i] - y[i]))
                    );
            }
            dis /= len;
            return dis;
        }
        public static double ComputeWebCosineSimilarity(Web X, Web Y)
        {
           double[] vector1 = X.iTFIDFs;
            double[] vector2 = Y.iTFIDFs;
            if (vector1.Length != vector2.Length)
                throw new Exception("DIFER LENGTH");
            double denom = (VectorLength(vector1) * VectorLength(vector2));
            if (denom == 0D)
                return 0D;
            else
                return (InnerProduct(vector1, vector2) / denom);
        }
        static double getCosDistance(Web coord, double[] center)
        {
            double[] vector1 = coord.iTFIDFs;
            double[] vector2 = center;
            if (vector1.Length != vector2.Length)
                throw new Exception("DIFER LENGTH");
            double denom = (VectorLength(vector1) * VectorLength(vector2));
            if (denom == 0D)
                return 0D;
            else
                return (InnerProduct(vector1, vector2) / denom);
        }
        public static double VectorLength(double[] vector)
        {
            double sum = 0.0D;
            for (int i = 0; i < vector.Length; i++)
                sum = sum + (vector[i] * vector[i]);

            return (double)Math.Sqrt(sum);
        }
        public static double InnerProduct(double[] vector1, double[] vector2)
        {

            if (vector1.Length != vector2.Length)
                throw new Exception("DIFFER LENGTH ARE NOT ALLOWED");


            double result = 0D;
            for (int i = 0; i < vector1.Length; i++)
                result += vector1[i] * vector2[i];

            return result;
        }
        private void InitRandom()
        {
            WebDistanceCache = new double[_webCount, _webCount];
            for(int i=0;i<_webCount;i++)
            {
                for(int k=0;k<_webCount;k++)
                {
                    WebDistanceCache[i,k] =
                        (((double)(1))/ComputeWebCosineSimilarity(_webs[i],_webs[k]));
                }
            }
            Random r = new Random();
            int tt = r.Next(9);
            _clusterAssignments[tt] = 0;
            _clusters[0] = new WawaCluster(tt, _webs[tt].iTFIDFs);
            double LongestValue = double.MinValue;
            int LongestWeb = 0;
            for(int i=0;i<_webCount;i++)
            {
                if(WebDistanceCache[tt,i]> LongestValue)
                {
                    LongestValue = WebDistanceCache[tt,i];
                    LongestWeb = i;
                }
            }
            _clusters[1] = new WawaCluster(LongestWeb, _webs[LongestWeb].iTFIDFs);
            double[] Minarr = new double[_webCount];
            double[] MinarrValue = new double[_webCount];
/*            double NearestValue = double.MaxValue;
            int NearestWeb = 0;*/
            for(int i=0;i<_webCount;i++)
            {
                if(WebDistanceCache[i,tt]<=WebDistanceCache[i,LongestWeb])
                {
                    MinarrValue[i] = WebDistanceCache[i,tt];
                    Minarr[i] = tt;
                }
                else
                {
                    MinarrValue[i] = WebDistanceCache[i,LongestWeb];
                    Minarr[i] = LongestWeb;
                }
            }
            int xx = 0;
            double MAX = double.MinValue;
            for (int i = 0; i < _webCount; i++)
            {
                if(MinarrValue[i]>MAX)
                {
                    MAX = MinarrValue[i];
                    xx = i;
                }
            }
            double Sita = MAX / LongestValue;
            _clusters[2] = new WawaCluster(xx, _webs[xx].iTFIDFs);
        }
    }
}