为什么我们需要学习线性回归呢？

线性回归是解决回归类问题最常使用的算法模型，其算法思想和基本原理都是由多元统计分析发展而来，但在数据挖掘和机器学习领域中，也是不可多得的行之有效的算法模型。一方面，线性回归蕴藏的机器学习思想非常值得借鉴和学习，并且随着时间发展，在线性回归的基础上还诞生了许多功能强大的非线性模型。

可见，学习线性回归确实非常重要。

1 概述

在正式进入到回归分析的相关算法讨论之前，我们需要对有监督学习算法中的回归问题进行进一步的分析和理解。虽然回归问题和分类问题同属于有监督学习范畴，但实际上，回归问题要远比分类问题更加复杂。

首先是关于输出结果的对比，分类模型最终输出结果为离散变量，而离散变量本身包含信息量较少，其本身并不具备代数运算性质，因此其评价指标体系也较为简单，最常用的就是混淆矩阵以及ROC曲线。而回归问题最终输出的是连续变量，其本身不仅能够代数运算，且还具有更"精致"的方法，希望对事物运行的更底层原理进行挖掘。即回归问题的模型更加全面、完善的描绘了事物客观规律，从而能够得到更加细粒度的结论。因此，回归问题的模型往往更加复杂，建模所需要数据所提供的信息量也越多，进而在建模过程中可能遇到的问题也越多。

2 线性回归与机器学习

我们在进行机器学习算法学习过程中，仍然需要对线性回归这个统计分析算法进行系统深入的学习。但这里需要说明的是，线性回归的建模思想有很多理解的角度，此处我们并不需要从统计学的角度来理解、掌握和应用线性回归算法，很多时候，利用机器学习的思维来理解线性回归，会是一种更好的理解方法，这也将是我们这部分内容讲解线性回归的切入角度。

3 线性回归的机器学习表示方法

3.1 核心逻辑

任何机器学习算法首先都有一个最底层的核心逻辑，当我们在利用机器学习思维理解线性回归的时候，首先也是要探究其底层逻辑。值得庆辛的是，虽然线性回归源于统计分析，但其算法底层逻辑和机器学习算法高度契合。

在给定n个属性描绘的客观事物 z = ( x 1 , x 2 , . . . , x n ) z=(x_1,x_2,...,x_n) z=(x1​,x2​,...,xn​)中，每个 都用于描绘某一次观测时事物在某个维度表现出来的数值属性值。当我们在建立机器学习模型捕捉事物运行的客观规律时，本质上是希望能够综合这些维度的属性值来描绘事物最终运行结果，而最简单的综合这些属性的方法就是对其进行加权求和汇总，这即是线性回归的方程式表达形式： y ^ = w 0 + w 1 x i 1 + w 2 x i 2 + . . . + + w n x i n \hat y=w_0+w_1x_{i1}+w_2x_{i2}+...++w_nx_{in} y^​=w0​+w1​xi1​+w2​xi2​+...++wn​xin​ w w w被统称为模型的参数，其中 w 0 w_0 w0​被称为截距(intercept)， w 1 w_1 w1​~ w n w_n wn​被称为回归系数(regression coeffiffifficient)，有时也是使用 β \beta β或者 θ \theta θ来表示。这个表达式，其实就和我们小学时就无比熟悉的 y = a x + b y=ax+b y=ax+b是同样的性质。其中 x i 1 x_{i1} xi1​是我们的目标变量，也就是标签。 是样本 i i i上的特征不同特征。如果考虑我们有m个样本，则回归结果可以被写作： y ^ = w 0 + w 1 x 1 + w 2 x 2 + . . . + + w n x n \hat y=w_0+w_1x_{1}+w_2x_{2}+...++w_nx_{n} y^​=w0​+w1​x1​+w2​x2​+...++wn​xn​其中 y y y是包含了m个全部的样本的回归结果的列向量（结构为(m,1)，由于只有⼀列，以列的形式表示，所以叫做列向量）。注意，我们通常使用粗体的小写字母来表示列向量，粗体的大写字母表示矩阵或者行列式。我们可以使用矩阵来表示这个方程，其中 可以被看做是⼀个结构为(n+1,1)的列矩阵， 是⼀个结构为(m,n+1)的特征矩阵，则有： [ y ^ 1 y ^ 2 y ^ 3 . . . y ^ m ] = [ 1 x 11 x 12 x 13 . . . x 1 n 1 x 21 x 22 x 23 . . . x 2 n 1 x 31 x 32 x 33 . . . x 3 n . . . 1 x m 1 x m 2 x m 3 . . . x m n ] ∗ [ w ^ 1 w ^ 2 w ^ 3 . . . w ^ n ] \begin{bmatrix} \hat y_1 \\ \hat y_2 \\ \hat y_3 \\ ... \\ \hat y_m \\ \end{bmatrix}=\begin{bmatrix} 1 & x_{11} & x_{12} & x_{13} & ... & x_{1n} \\ 1 & x_{21} & x_{22} & x_{23} & ... & x_{2n} \\ 1 & x_{31} & x_{32} & x_{33} & ... & x_{3n} \\ ... \\ 1 & x_{m1} & x_{m2} & x_{m3} & ... & x_{mn}\end{bmatrix} * \begin{bmatrix} \hat w_1 \\ \hat w_2 \\ \hat w_3 \\ ... \\ \hat w_n \\ \end{bmatrix} ⎣⎢⎢⎢⎢⎡​y^​1​y^​2​y^​3​...y^​m​​⎦⎥⎥⎥⎥⎤​=⎣⎢⎢⎢⎢⎡​111...1​x11​x21​x31​xm1​​x12​x22​x32​xm2​​x13​x23​x33​xm3​​............​x1n​x2n​x3n​xmn​​⎦⎥⎥⎥⎥⎤​∗⎣⎢⎢⎢⎢⎡​w^1​w^2​w^3​...w^n​​⎦⎥⎥⎥⎥⎤​ y ^ = X w \hat y = Xw y^​=Xw线性回归的任务，就是构造⼀个预测函数来映射输入的特征矩阵 和标签值 的线性关系，这个预测函数在不同的教材上写法不同，可能写作 f ( x ) f(x) f(x)， y w ( x ) y_w(x) yw​(x) ，或者 h ( x ) h(x) h(x)等等形式，但无论如何，这个预测函数的本质就是我们需要构建的模型。

3.2 优化目标

对于线性回归而言，预测函数 y ^ = X w \hat y = Xw y^​=Xw就是我们的模型，在机器学习我们也称作 “决策数”。其中只有 w w w是未知的，所以线性回归原理的核心就是找出模型的参数向量 w w w 。但我们怎样才能够求解出参数向量呢？我们需要依赖一个重要概念：损失函数。

在之前的算法学习中，我们提到过两种模型表现：在训练集上的表现，和在测试集上的表现。我们建模，是追求模型在测试集上的表现最优，因此模型的评估指标往往是⽤来衡量模型在测试集上的表现的。然而，线性回归有着基于训练数据求解参数 的需求，并且希望训练出来的模型能够尽可能地拟合训练数据，即模型在训练集上的预测准确率越靠近100%越好。

因此，我们使用损失函数这个评估指标，来衡量系数为 w w w的模型拟合训练集时产生的信息损失的大小，并以此衡量参数 w w w的优劣。如果用一组参数建模后，模型在训练集上表现良好，那我们就说模型拟合过程中的损失很小，损失函数的值很小，这一组参数就优秀；相反，如果模型在训练集上表现糟糕，损失函数就会很大，模型就训练不足，效果较差，这一组参数也就比较差。即是说，我们在求解参数 w w w时，追求损失函数最小，让模型在训练数据上的拟合效果最优，即预测准确率尽量靠近100%。

（注意：对于非参数模型没有损失函数，比如KNN、决策树）

对于有监督学习算法而言，建模都是依据有标签的数据集，回归类问题则是对客观事物的⼀个定量判别。这里以 y i y_i yi​作为第 i i i行数据的标签，且 y i y_i yi​为连续变量， x i x_i xi​为第 i i i行特征值所组成的向量，则线性回归建模优化方向就是希望模型判别的 y ^ i \hat y_i y^​i​尽可能地接近实际的 y i y_i yi​。而对于连续型变量而言，邻近度度量方法可采用 S S E SSE SSE来进行计算， S S E SSE SSE称作「残差平方和」，也称作「误差平方和」或者「离差平方和」。

因此我们的优化目标可用下述方程来进行表示： m i n w ∑ i = 1 m ( y i − y ^ i ) 2 = m i n w ∑ i = 1 m ( y i − X i w ) 2 \underset {w}{min}\sum_{i=1}^{m}{(y_i-\hat y_i)^2}=\underset {w}{min}\sum_{i=1}^{m}{(y_i-X_iw)^2} wmin​i=1∑m​(yi​−y^​i​)2=wmin​i=1∑m​(yi​−Xi​w)2来看⼀个简单的⼩例子。假设现在 w w w为[1,2]这样⼀个向量，求解出的模型为 y = x 1 + 2 x 2 y=x_1+2x_2 y=x1​+2x2​。

样本	特征1	特征2	真实标签
0	1	0.5	3
1	-1	0.5	2

则我们的损失函数的值就是： ( 3 − ( 1 ∗ 1 + 2 ∗ 0.5 ) ) 2 + ( 2 − ( 1 ∗ ( − 1 ) + 2 ∗ 0.5 ) ) 2 ( y 1 − y ^ 1 ) 2 + ( y 2 − y ^ 2 ) 2 (3-(1*1+2*0.5))^2+(2-(1*(-1)+2*0.5))^2 \\ (y_1- \hat y_1)^2 + (y_2- \hat y_2)^2 (3−(1∗1+2∗0.5))2+(2−(1∗(−1)+2∗0.5))2(y1​−y^​1​)2+(y2​−y^​2​)2

3.3 最小二乘法

现在问题转换成了求解 S S E SSE SSE最小化的参数向量 w w w，这种通过最小化真实值和预测值之间的 S S E SSE SSE来求解参数的方法叫做最小二乘法。

3.3.1 回顾一元线性回归的求解过程

下面我们来用代码尝试一下。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#生成横坐标   范围 0 -10
np.random.seed(420)
x = np.random.rand(50) * 10 #50个点
x

# y = 2x - 5
#添加扰动项
np.random.seed(420)
y = 2 * x - 5 + np.random.randn(50) #正太分布下的随机数

plt.plot(x,y,'o')

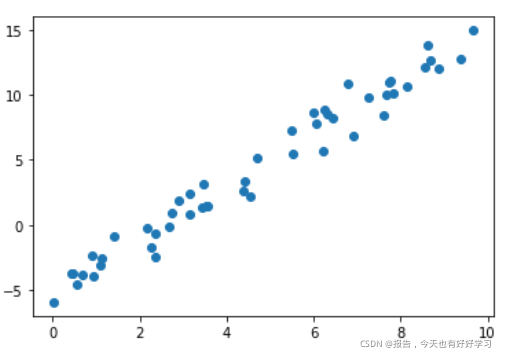
现在对上图数据进行拟合：

from sklearn.linear_model import LinearRegression

#实例化
lr = LinearRegression(fit_intercept=True)

x2 = x.reshape(-1,1)

# 训练模型
lr.fit(x2, y)

# 生成绘制直线的横坐标
xfit = np.linspace(0,10,100) #从0到10  生成100个

xfit2 = xfit.reshape(-1,1)

yfit = lr.predict(xfit2) #预测

#画出点的直线
plt.plot(xfit,yfit)
#画出原来训练集的点
plt.plot(x,y,'o')

看上去效果还是不错的。

假设该拟合直线为 y ^ = w 0 + w 1 x \hat y = w_0+w_1x y^​=w0​+w1​x。现在我们的目标是使得该拟合直线的总的残差和达到最小，也就是最小化 S S E SSE SSE。

我们令该直线是以均值为核心的「均值回归」，即散点的 x ˉ \bar x xˉ 和 y ˉ \bar y yˉ​ 必经过这条直线： y ˉ = w 0 + w 1 x ˉ \bar y = w_0+w_1 \bar x yˉ​=w0​+w1​xˉ对于真实值y来说，我们可以得到： y = w 0 + w 1 x + ϵ y = w_0+w_1 x + \epsilon y=w0​+w1​x+ϵ这里的 ϵ \epsilon ϵ即为「残差」，对其进行变形，则残差平⽅和 S S E SSE SSE就为： ∑ ϵ 2 = ∑ ( y − w 0 − w 1 x ) 2 \sum{\epsilon^2=\sum (y-w_0-w_1x)^2} ∑ϵ2=∑(y−w0​−w1​x)2要求得残差平方和最小值，我们通过微积分求偏导算其极值来解决。这⾥我们计算残差最小对应的参数 w 1 w_1 w1​：

此时，使得 S S E SSE SSE最小的量 w ^ 0 \hat w_0 w^0​， w ^ 1 \hat w_1 w^1​称为总体参数 w 0 w_0 w0​， w 1 w_1 w1​的最小⼆乘估计值，预测⽅程 y ^ = w ^ 0 + w ^ 1 x \hat y = \hat w_0+\hat w_1x y^​=w^0​+w^1​x 称为最小⼆乘直线。

3.3.2 多元线性回归求解参数

更⼀般的情形，还记得我们刚才举的小例子么？如果我们有两列特征属性，则损失函数为： ( y 1 − y ^ 1 ) 2 + ( y 2 − y ^ 2 ) 2 (y_1-\hat y_1)^2+(y_2-\hat y_2)^2 (y1​−y^​1​)2+(y2​−y^​2​)2这样的形式如果矩阵来表达，可以写成： [ ( y 1 − y ^ 1 ) ( y 2 − y ^ 2 ) ] ∗ [ ( y 1 − y ^ 1 ) ( y 2 − y ^ 2 ) ] = ( y − X w ) T ( y − X w ) \begin{bmatrix} (y_1-\hat y_1)(y_2-\hat y_2) \\ \end{bmatrix}*\begin{bmatrix} (y_1-\hat y_1) \\ (y_2-\hat y_2) \\ \end{bmatrix} \\ =(y-Xw)^T(y-Xw) [(y1​−y^​1​)(y2​−y^​2​)​]∗[(y1​−y^​1​)(y2​−y^​2​)​]=(y−Xw)T(y−Xw)矩阵相乘是对应未知元素相乘相加，就会得到和上面的式子一模一样的结果。

我们同时对 w w w求偏导：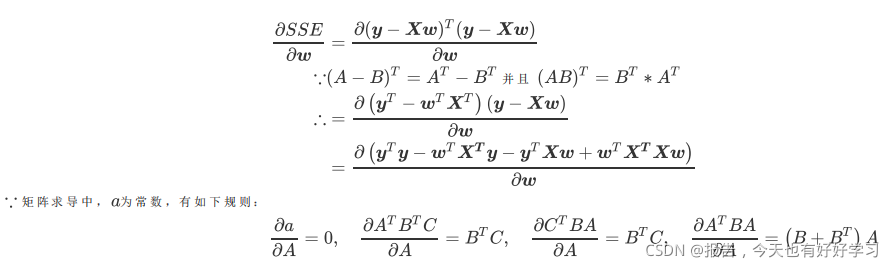
可得到：

我们让求导后的一阶导数为0：

到了这里，我们希望能够将 w w w留在等式的左边，其他与特征矩阵有关的部分都放到等式的右边，如此就可以求出 w w w的最优解了。这个功能非常容易实现，只需要我们左乘 X T X X^TX XTX的逆矩阵就可以。
在这里，逆矩阵存在的充分必要条件是特征矩阵不存在多重共线性。我们将会在后面详细讲解多重共线性这个主题。

假设矩阵的逆是存在的，此时我们的 w w w就是我们参数的最优解。求解出这个参数向量，我们就解出了我们的 X w Xw Xw，也就能够计算出我们的预测值 y ^ \hat y y^​了。

结束语

如果看到这里开始有点乱了，没有关系，本次介绍线性回归的重点是在于让你从机器学习的角度来理解和使用线性回归，如果统计学的知识你感觉不好掌握的话，可以后面再多花点时间去巩固，无须自我否定。

在下一篇文章中，我会详细讲解如何利用Python实现线性回归，以及如何评估回归模型的好坏，当然也会进一步介绍多重共线性及其应用，也欢迎大家关注我下面推荐的专栏。

推荐关注的专栏

👨‍👩‍👦‍👦 机器学习：分享机器学习实战项目和常用模型讲解
👨‍👩‍👦‍👦 数据分析：分享数据分析实战项目和常用技能整理

机器学习系列往期回顾

💙 你真的了解分类模型评估指标都有哪些吗？【附Python代码实现】
🖤 一文带你用Python玩转决策树 ❤️画出决策树&各种参数详细说明❤️决策树的优缺点又有哪些？
🧡 开始学习机器学习时你必须要了解的模型有哪些？机器学习系列之决策树进阶篇
💚 开始学习机器学习时你必须要了解的模型有哪些？机器学习系列之决策树基础篇
❤️ 以❤️简单易懂❤️的语言带你搞懂有监督学习算法【附Python代码详解】机器学习系列之KNN篇
💜 开始学习机器学习之前你必须要了解的知识有哪些？机器学习系列入门篇

往期内容回顾

🖤 我和关注我的前1000个粉丝“合影”啦！收集前1000个粉丝进行了一系列数据分析，收获满满
💚 MySQL必须掌握的技能有哪些？超细长文带你掌握MySQL【建议收藏】
💜 Hive必须了解的技能有哪些？万字博客带你掌握Hive❤️【建议收藏】

CSDN@报告，今天也有好好学习