文章目录
- 一、线性表的定义和特点及案例引入
- 1.线性表的定义和特点
- 2.案例引入
- (1) 一元多项式的运算
- (2) 稀疏多项式的运算
- (3) 图书信息管理系统
- 二、线性表的类型定义
- 三、线性表的顺序表示和实现
- 1.初始化顺序表
- 2.顺序表取值
- 3.顺序表查找
- 4.顺序表的插入
- 5.顺序表的删除
- 6.基本操作补充
- 7.顺序表的特点
- 四、线性表的链式表示和实现
- 1.链表介绍及单链表、双链表、循环链表基本定义
- 2.三个典型问题
- 3.链表的特点及优缺点
- 五、单链表
- 1.单链表的定义和实现
- 2.单链表的存储结构定义
- 3.初始化单链表
- 4.基本操作补充
- 5.单链表的取值
- 6.单链表的查找
- 7.单链表的插入
- 8.单链表的删除
- 9.链表运算时间效率分析
- 六、循环链表
- 1.循环链表的基本形态:
- 2.循环链表特点
- 3.循环链表的合并
- 七、双向链表
- 1.双向链表基本形态及特点
- 2.双向链表的插入
- 3.双向链表的删除
- 八、顺序表和链表的比较
- 九、线性表的应用
- 1.线性表的合并
- 2. 顺序有序表的合并
- 3.有序链表的合并
- 十、案例实现与分析
- 1.多项式的创建
- 2.多项式的相加
- 十一、单链表、循环链表、双向链表的时间效率的比较
- 十二、总结
线性表的知识是数据结构中的重点及基础,涉及到的知识会比较多,但对线性表的操作反复进行理解与实践会使你对线性表的理解更加深刻、学的更好。
一、线性表的定义和特点及案例引入
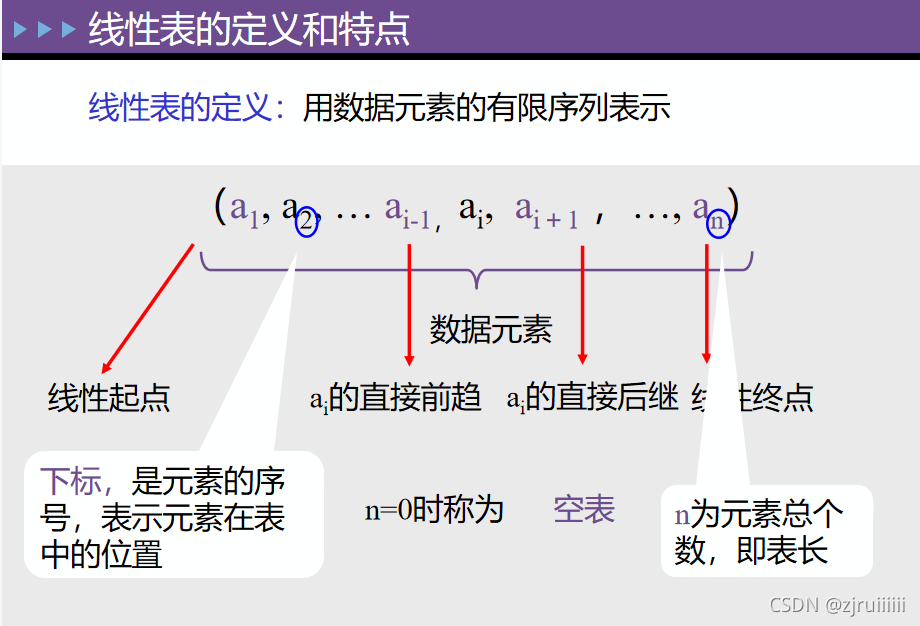
1.线性表的定义和特点
了解线性表内元素的关系,书上对这部分也有了比较详细的介绍,在此我仅用图把它们的关系罗列出来。
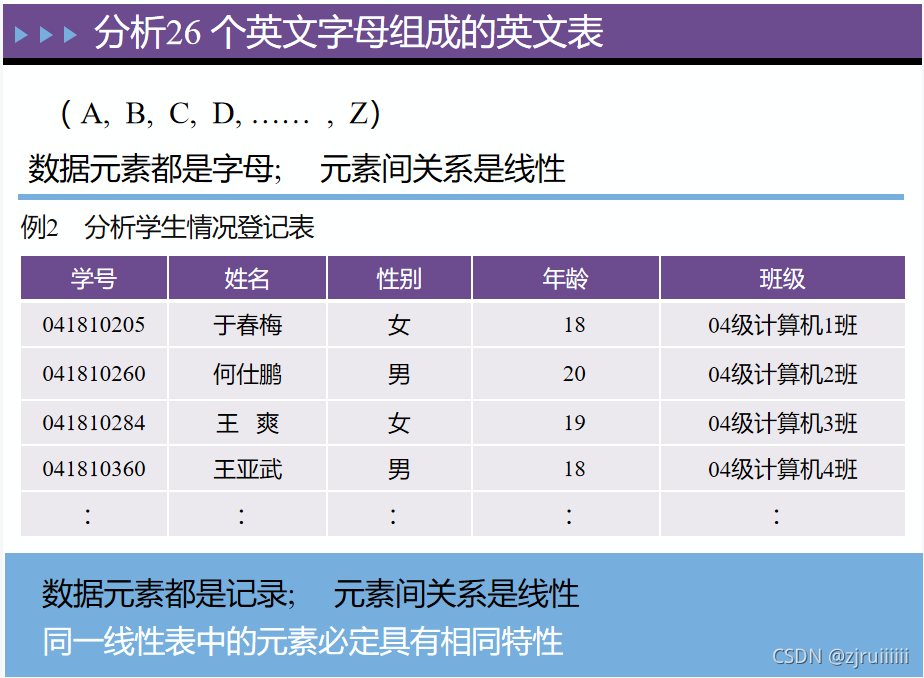
2.案例引入
(1) 一元多项式的运算
了解每一项的指数与其在线性表中的对应关系。

创建新数组c,分别从头遍历比较a和b的每一项,指数相同,对应系数相加,若其和不为零,则在c中增加一个新项。指数不相同,则将指数较小的项复制到c中。当一个多项式已遍历完毕时,将另一个剩余项依次复制到c中即可。

(2) 稀疏多项式的运算
对于稀疏多项式,每个项的指数不再代表一个数组的下标,因此分别要开辟空间存放系数和指数。
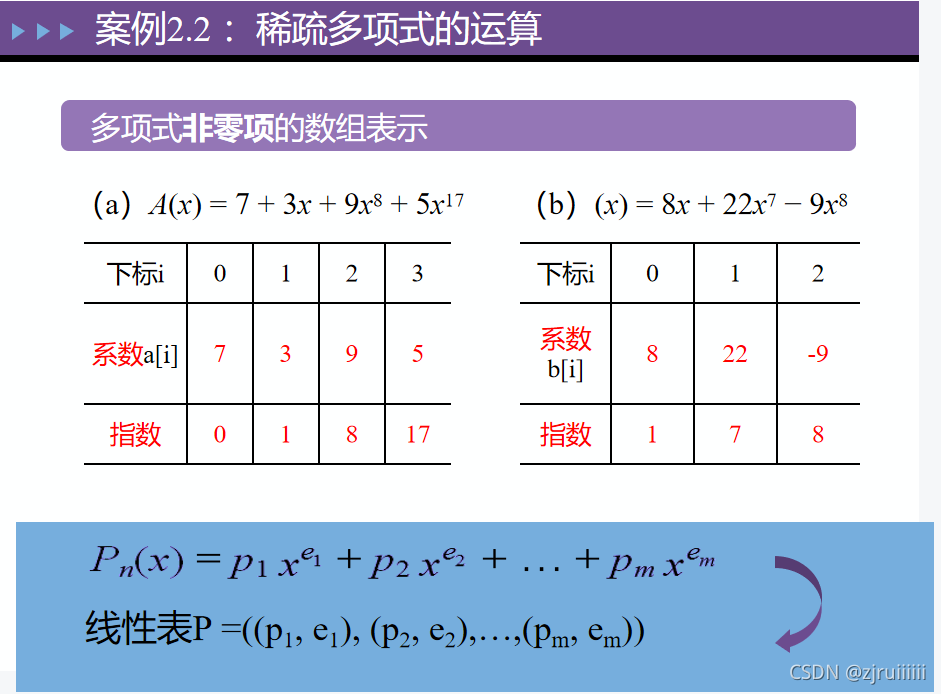
对于指数不是依次增加的多项式,要学会如何去存储数据。例如:

因此当我们在存储上面两个多项式时,如果仍然使用顺序表进行存储,则缺点有:(1)存储空间分配不灵活。(2)运算的空间复杂度高。我们应该使用链式结构进行存储。
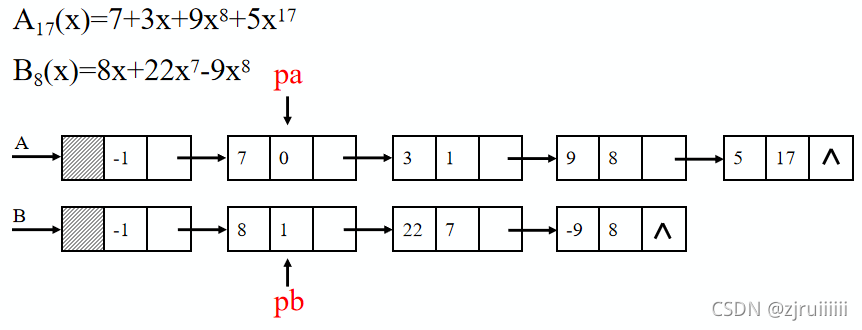
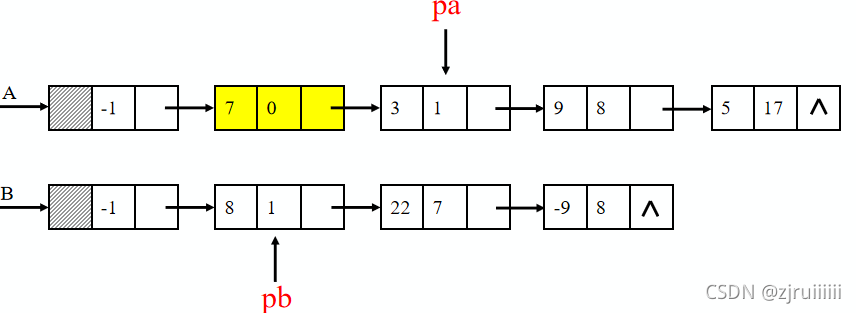
进行上面两个多项式的相加:
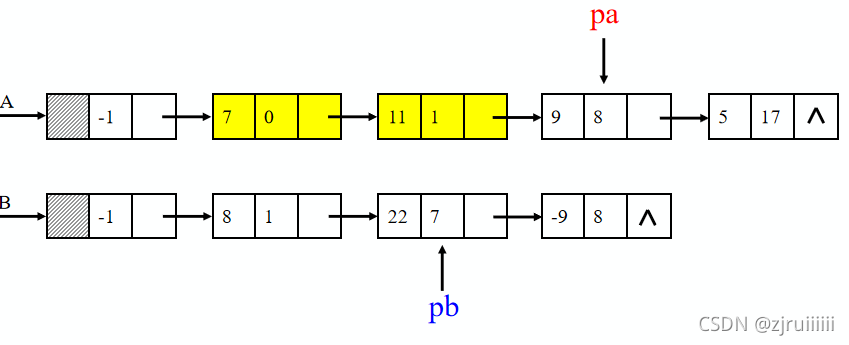
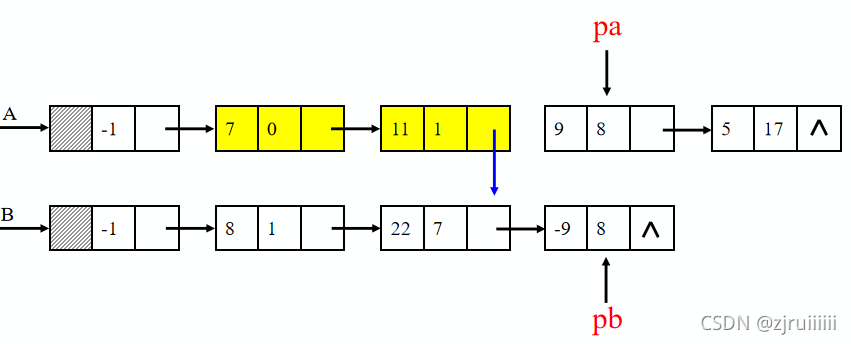
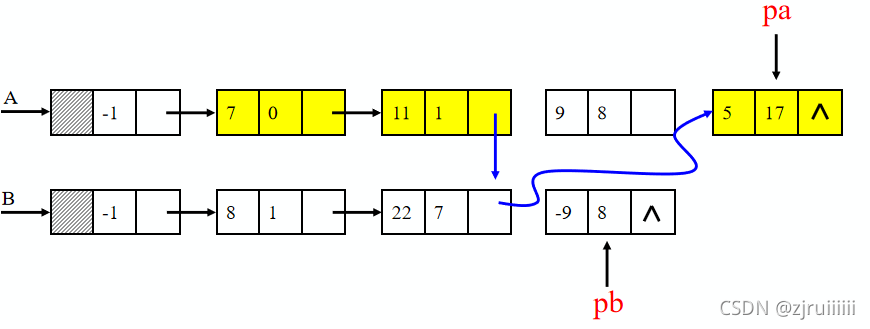
分析:首先我们从A的结点开始,往后一位则是指数为0,系数为7的结点,与B进行比较,发现B中没有指数为0的结点,我们不作处理,再对链表A后面的结点进行分析。发现链表A与链表B都有指数为1的结点,则将它们的系数相加放在链表A中。以此类推进行分析。过程与结果如下图:
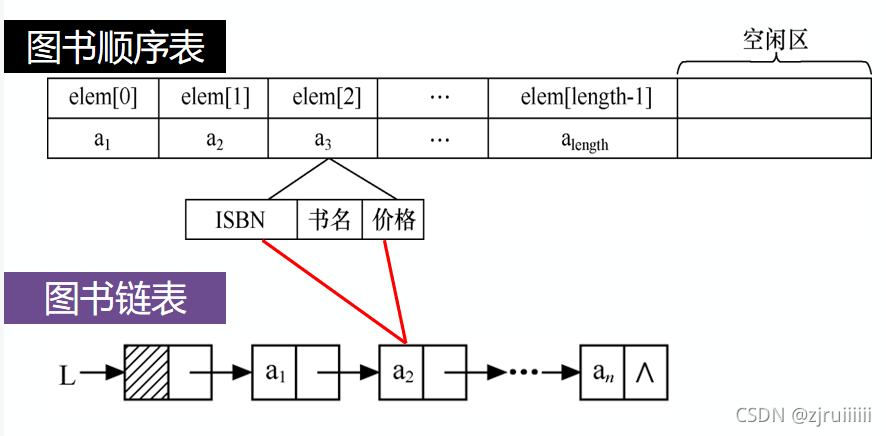
(3) 图书信息管理系统
对于图书信息管理系统,我们经常会有查找、插入、删除、修改、排序、计数等操作,用顺序表或链表存储图书信息的方式如下:
小结:
(1) 线性表中数据元素的类型可以为简单类型,也可以为复杂类型。
(2) 许多实际应用问题所涉的基本操作有很大相似性,不应为每个具体应用单独编写一个程序,过于耗费成本。
(3) 从具体应用中抽象出共性的逻辑结构和基本操作(抽象数据类型),然后实现其存储结构和基本操作。
二、线性表的类型定义
线性表主要分为顺序表与链表,它们的重要基本操作有初始化、取值、查找、插入、删除。顺序表的存储方式为随机存储,链表的存储方式为顺序存储。
顺序存储定义:把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构。简言之,逻辑上相邻,物理上也相邻。
顺序存储方法:用一组地址连续的存储单元依次存储线性表的元素,可通过数组V[n]来实现。
三、线性表的顺序表示和实现
数据元素相互之间的存储关系:

顺序表的类型定义:
#define MAXSIZE 100 //最大长度
typedef struct
{
ElemType *elem; //指向数据元素的基地址
int length; //线性表的当前长度
}SqList;
图书表的顺序存储结构类型定义:
#define MAXSIZE 10000 //图书表可能达到的最大长度
typedef struct //图书信息定义
{
char no[20]; //图书ISBN
char name[50]; //图书名字
float price; //图书价格
}Book;
typedef struct
{
Book *elem; //存储空间的基地址
int length; //图书表中当前图书个数
}SqList; //图书表的顺序存储结构类型为SqList
以下是对顺序表操作的具体步骤,对于简单的代码,在代码后面我注释说明;而相对复杂的代码,我再具体进行解释及说明。
1.初始化顺序表
方法1:参数为引用类型:
Status InitList_Sq(SqList &L) //构造一 个空的顺序表L
{
L.elem=new ElemType[MAXSIZE]; //为顺序表分配空间
if(!L.elem) exit(OVERFLOW); //存储分配失败
L.length=0; //空表长度为0
return OK;
}
方法2:参数用指针类型:
Status InitList_Sq(SqList *L) //构造一个空的顺序表L
{
L-> elem=new ElemType[MAXSIZE]; //为顺序表分配空间
if(! L-> elem) exit(OVERFLOW); //存储分配失败
L-> length=0; //空表长度为0
return OK;
}
2.顺序表取值
获取顺序表L中的某个数据元素的内容:
int GetElem(SqList L,int i,ElemType &e)
{
if (i<1||i>L.length) return ERROR;
//判断i值是否合理,若不合理,返回ERROR
e=L.elem[i-1]; //第i-1的单元存储着第i个数据
return OK;
}
这个算法的时间复杂度为O(1)。
3.顺序表查找
在线性表L中查找值为e的数据元素:
int LocateELem(SqList L,ElemType e)
{
for (i=0;i< L.length;i++)
if (L.elem[i]==e) return i+1; //返回查找值为e的位置
return 0;
}
要求顺序表查找算法的时间复杂度要先了解一个知识:什么是平均查找长度?(简称ASL),书上对平均查找长度有明确的解释,我这里就简单地解释一下。平均查找长度就是(每个元素被操作的概率)乘以(最坏情况下n次到第i个元素的和除以2)。例如查找操作,假设一共有n个元素,因为每一个元素都有被查找的可能,因此概率为n分之1,假设最坏情况是循环第n次才找到该元素,因此时间复杂度就为n分之1乘以i的1到n的和。
4.顺序表的插入
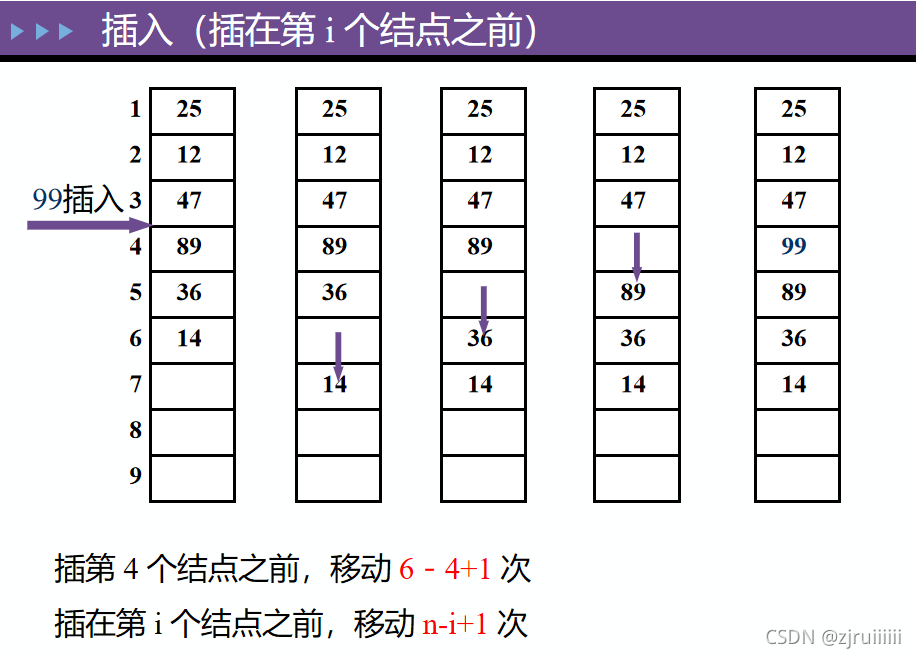
在线性表L中第i个数据元素之前插入数据元素e:
Status ListInsert_Sq(SqList &L,int i ,ElemType e)
{
if(i<1 || i>L.length+1) return ERROR; //i值不合法
if(L.length==MAXSIZE) return ERROR; //当前存储空间已满
for(j=L.length-1;j>=i-1;j--)
L.elem[j+1]=L.elem[j]; //插入位置及之后的元素后移
L.elem[i-1]=e; //将新元素e放入第i个位置
++L.length; //表长增1
return OK;
}
时间复杂度为O(n)。
5.顺序表的删除
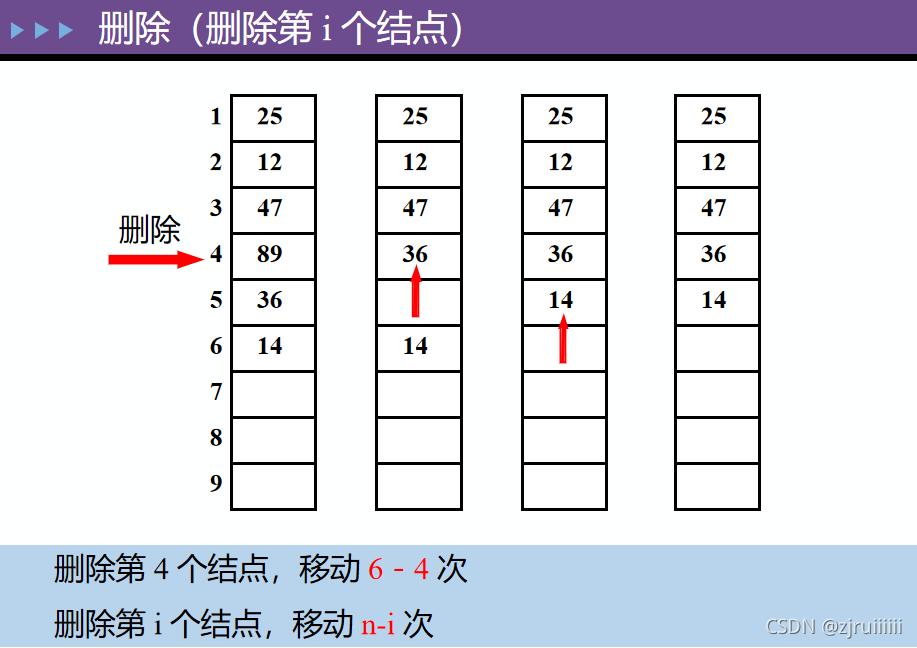
将线性表L中第i个数据元素删除:
Status ListDelete_Sq(SqList &L,int i)
{
if((i<1)||(i>L.length)) return ERROR; //i值不合法
for (j=i;j<=L.length-1;j++)
L.elem[j-1]=L.elem[j]; //被删除元素之后的元素前移
--L.length; //表长减1
return OK;
}
时间复杂度:O(n)。
6.基本操作补充
销毁线性表L:
void DestroyList(SqList &L)
{
if (L.elem) delete[]L.elem; //释放存储空间
}
清空线性表L:
void ClearList(SqList &L)
{
L.length=0; //将线性表的长度置为0
}
求线性表L的长度:
int GetLength(SqList L)
{
return (L.length);
}
判断线性表L是否为空:
int IsEmpty(SqList L)
{
if (L.length==0) return 1;
else return 0;
}
7.顺序表的特点
(1) 利用数据元素的存储位置表示线性表中相邻数据元素之间的前后关系,即线性表的逻辑结构与存储结构一致。
(2) 在访问线性表时,可以快速地计算出任何一个数据元素的存储地址。因此可以粗略地认为,访问每个元素所花时间相等。
这种存取元素的方法被称为随机存取法。
优点:
(1) 存储密度大(结点本身所占存储量/结点结构所占存储量)。
(2) 可以随机存取表中任一元素。
缺点:
(1) 在插入、删除某一元素时,需要移动大量元素。
(2) 浪费存储空间。
(3) 属于静态存储形式,数据元素的个数不能自由扩充。
因此,为了克服顺序表的缺点而产生了链表。
四、线性表的链式表示和实现
1.链表介绍及单链表、双链表、循环链表基本定义
结点:数据元素的存储映像。由数据域和指针域两部分组成。
链表: n 个结点由指针链组成一个链表。它是线性表的链式存储映像,称为线性表的链式存储结构。
链式存储结构定义:
结点在存储器中的位置是任意的,即逻辑上相邻的数据元素在物理上不一定相邻。
线性表的链式表示又称为非顺序映像或链式映像。
链表示意图:
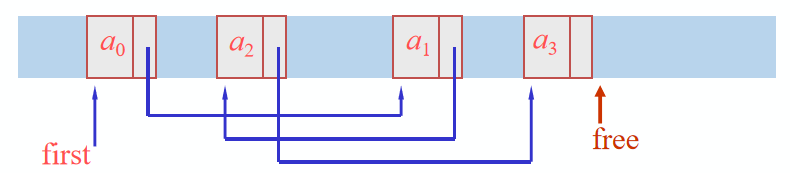
链表各结点由两个域组成:
数据域:存储元素数值数据。
指针域:存储直接后继结点的存储位置。

单链表、双链表、循环链表:
结点只有一个指针域的链表,称为单链表或线性链表。
有两个指针域的链表,称为双链表。
首尾相接的链表称为循环链表。
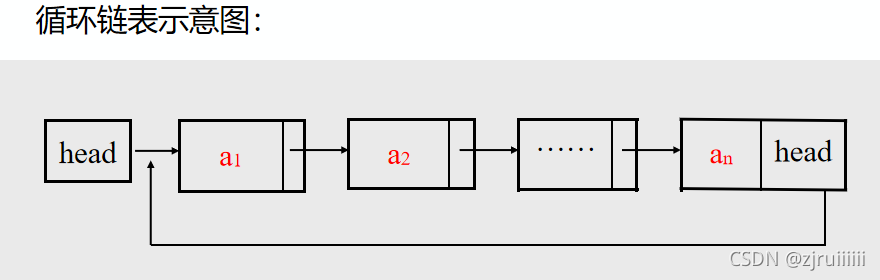
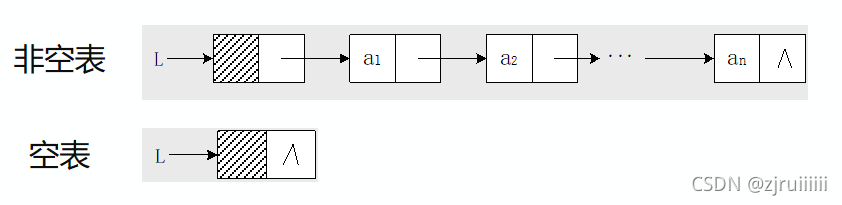
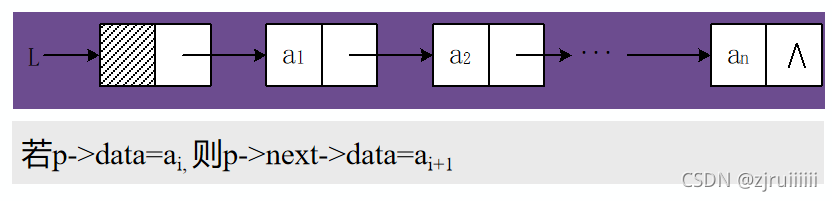
头指针、头结点、首元结点:
头指针是指向链表中第一个结点的指针。
首元结点是指链表中存储第一个数据元素a1的结点。
头结点是在链表的首元结点之前附设的一个结点;数据域内只放空表标志和表长等信息。
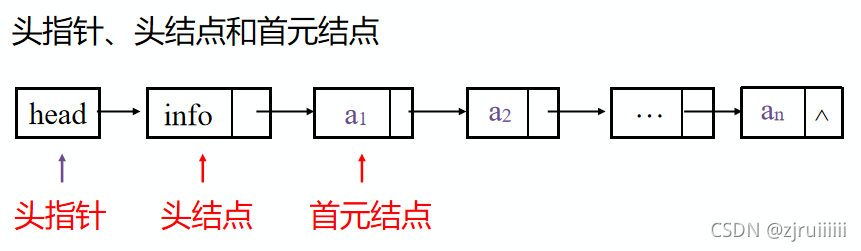
链表有两种表现形式:头结点的有无。
2.三个典型问题
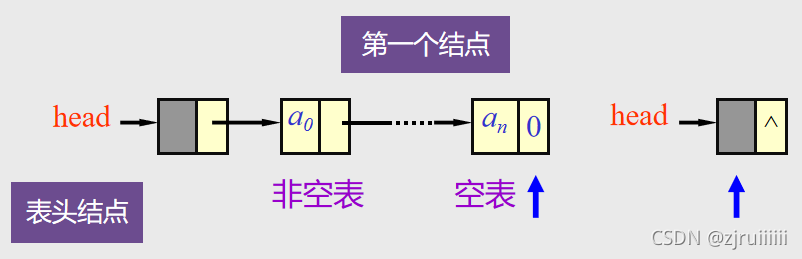
问题一:如何表示空表?
答:有头结点时,当头结点的指针域为空时表示空表。
如图所示:
问题二:在链表中设置头结点有什么好处?
答:
(1) 便于首元结点的处理。首元结点的地址保存在头结点的指针域中,所以在链表的第一个位置上的操作和其它位置一致,无须进行特殊处理。
(2) 便于空表和非空表的统一处理。无论链表是否为空,头指针都是指向头结点的非空指针,因此空表和非空表的处理也就统一了。
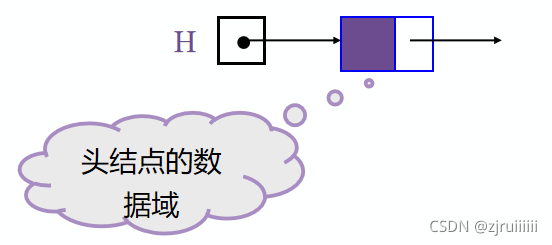
问题三:头结点的数据域内装的是什么?
答:头结点的数据域可以为空,也可存放线性表长度等附加信息,但此结点不能计入链表长度值。
如图所示:
3.链表的特点及优缺点
链表(链式存储结构)的特点:
(1) 结点在存储器中的位置是任意的,即逻辑上相邻的数据元素在物理上不一定相邻。
(2) 访问时只能通过头指针进入链表,并通过每个结点的指针域向后扫描其余结点,所以寻找第一个结点和最后一个结点所花费的时间不等。
这种存取元素的方法被称为顺序存取法。
优点:
(1) 数据元素的个数可以自由扩充。
(2) 插入、删除等操作不必移动数据,只需修改链接指针,修改效率较高。
缺点:
(1) 存储密度小。
(2) 存取效率不高,必须采用顺序存取,即存取数据元素时,只能按链表的顺序进行访问(顺藤摸瓜)。
五、单链表
1.单链表的定义和实现
- 单链表是由表头唯一确定,因此单链表可以用头指针的名字来命名。
- 若头指针名是L,则把链表称为表L 。
2.单链表的存储结构定义
typedef struct Lnode
{
ElemType data; //数据域
struct LNode *next; //指针域
}LNode,*LinkList; //LNode指结点,*LinkList指的是指针
// *LinkList为Lnode类型的指针
LNode与*LinkList相等,创建的都是指针。

注意区分指针变量和结点变量两个不同的概念:
- 指针变量p:表示结点地址。
- 结点变量*p:表示一个结点。
后面的代码中会大量用到指针,我觉得用图来进行说明更方便理解。
3.初始化单链表
Status InitList_L(LinkList &L){
L=new LNode;//设置一个头结点
L->next=NULL;//头结点的指针域置空
return OK;
}
4.基本操作补充
单链表的销毁:
Status DestroyList_L(LinkList &L)
{
LinkList p;//设置指针p
while(L)
{
p=L;
L=L->next;
delete p; //删除结点
}
return OK;
}
清空单链表
Status ClearList(LinkList & L){
// 将L重置为空表
LinkList p,q;
p=L->next; //p指向第一个结点
while(p) //没到表尾
{
q=p->next; delete p; p=q;
}
L->next=NULL; //头结点指针域为空
return OK;
}
求单链表表长
int ListLength_L(LinkList L){
//返回L中数据元素个数
LinkList p;
p=L->next; //p指向第一个结点
i=0;
while(p){//遍历单链表,统计结点数
i++;
p=p->next; }
return i;
}
判断表是否为空
int ListEmpty(LinkList L)
{
//若L为空表,则返回1,否则返回0
if(L->next) //非空
return 0;
else
return 1;
}
5.单链表的取值
链表的查找:要从链表的头指针出发,顺着链域next逐个结点往下搜索,直至搜索到第i个结点为止。因此,链表不是随机存取结构。
算法步骤:
(1) 从第1个结点(L->next)顺链扫描,用指针p指向当前扫描到的结点,p初值p = L->next。
(2) j做计数器,累计当前扫描过的结点数,j初值为1。
(3) 当p指向扫描到的下一结点时,计数器j加1。
(4) 当j = i时,p所指的结点就是要找的第i个结点。
Status GetElem_L(LinkList L,int i,ElemType &e){
p=L->next;j=1; //初始化
while(p&&j<i){ //向后扫描,直到p指向第i个元素或p为空
p=p->next; ++j;
}
if(!p || j>i)return ERROR; //第i个元素不存在
e=p->data; //取第i个元素
return OK;
}//GetElem_L
6.单链表的查找
算法步骤:
(1) 从第一个结点起,依次和e相比较。
(2) 如果找到一个其值与e相等的数据元素,则返回其在链表中的“位置”或地址;
(3) 如果查遍整个链表都没有找到其值和e相等的元素,则返回或“NULL”。
1.返回L中值为e的数据元素的地址,查找失败返回NULL。
LNode *LocateELem_L (LinkList L,Elemtype e) {
p=L->next;
while(p &&p->data!=e)
p=p->next;
return p;
}
2.返回L中值为e的数据元素的位置序号,查找失败返回0。
int LocateELem_L (LinkList L,Elemtype e) {
//返回L中值为e的数据元素的位置序号,查找失败返回0
p=L->next; j=1;
while(p &&p->data!=e)
{p=p->next; j++;}
if(p) return j;
else return 0;
}
7.单链表的插入
1.任意位置插入:
算法步骤:

//在L中第i个元素之前插入数据元素e
Status ListInsert_L(LinkList &L,int i,ElemType e){
p=L;j=0;
while(p&&j<i−1){p=p->next;++j;} //寻找第i−1个结点
if(!p||j>i−1)return ERROR; //i大于表长 + 1或者小于1
s=new LNode; //生成新结点s
s->data=e; //将结点s的数据域置为e
s->next=p->next; //将结点s插入L中
p->next=s;
return OK;
}//ListInsert_L
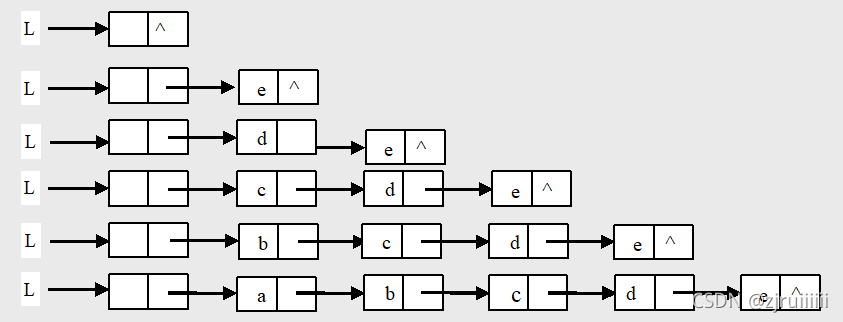
2.头插法
算法步骤:
从一个空表开始,重复读入数据:
(1) 生成新结点。
(2) 将读入数据存放到新结点的数据域中。
(3) 将该新结点插入到链表的前端。
void CreateList_F(LinkList &L,int n){
L=new LNode;
L->next=NULL; //先建立一个带头结点的单链表
for(i=n;i>0;--i){
p=new LNode; //生成新结点
cin>>p->data; //输入元素值
p->next=L->next;L->next=p; //插入到表头
}
}//CreateList_F
3.尾插法
算法步骤:
(1) 从一个空表L开始,将新结点逐个插入到链表的尾部,尾指针r指向链表的尾结点。
(2) 初始时,r同L均指向头结点。每读入一个数据元素则申请一个新结点,将新结点插入到尾结点后,r指向新结点。
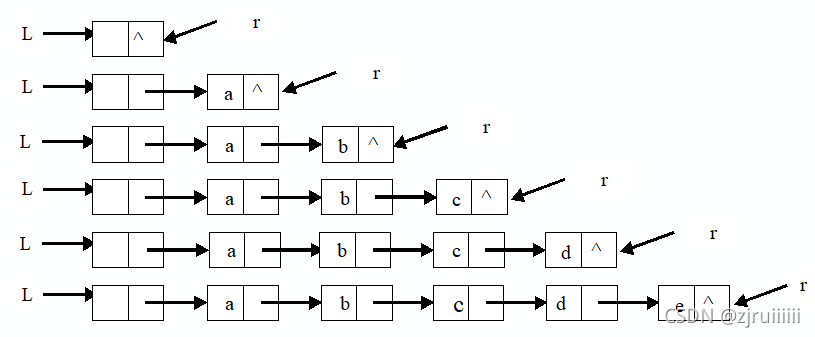
void CreateList_L(LinkList &L,int n){
//正位序输入n个元素的值,建立带表头结点的单链表L
L=new LNode;
L->next=NULL;
r=L; //尾指针r指向头结点
for(i=0;i<n;++i){
p=new LNode; //生成新结点
cin>>p->data; //输入元素值
p->next=NULL; r->next=p; //插入到表尾
r=p; //r指向新的尾结点
}
}//CreateList_L
8.单链表的删除
算法步骤:
(1) 找到ai-1存储位置p。
(2) 保存要删除的结点的值。
(3) 令p->next指向ai的直接后继结点。
(4) 释放结点ai的空间。
删除示意图:
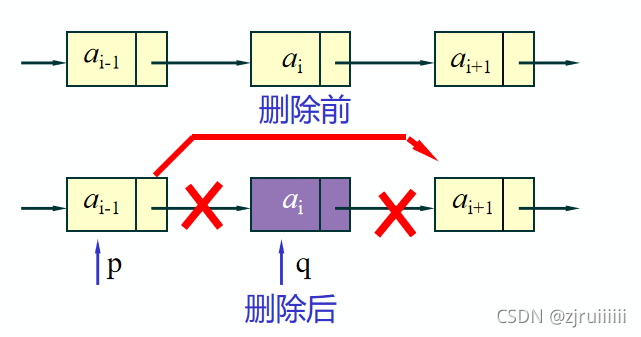
//将线性表L中第i个数据元素删除
Status ListDelete_L(LinkList &L,int i,ElemType &e){
p=L;j=0;
while(p->next &&j<i-1){ //寻找第i个结点,并令p指向其前驱
p=p->next; ++j;
}
if(!(p->next)||j>i-1) return ERROR; //删除位置不合理
q=p->next; //临时保存被删结点的地址以备释放
p->next=q->next; //改变删除结点前驱结点的指针域
e=q->data; //保存删除结点的数据域
delete q; //释放删除结点的空间
return OK;
}//ListDelete_L
9.链表运算时间效率分析
1.查找: 因线性链表只能顺序存取,即在查找时要从头指针找起,查找的时间复杂度为 O(n)。
2.插入和删除: 因线性链表不需要移动元素,只要修改指针,一般情况下时间复杂度为 O(1)。
3.但是,如果要在单链表中进行前插或删除操作,由于要从头查找前驱结点,所耗时间复杂度为 O(n) 。
六、循环链表
1.循环链表的基本形态:
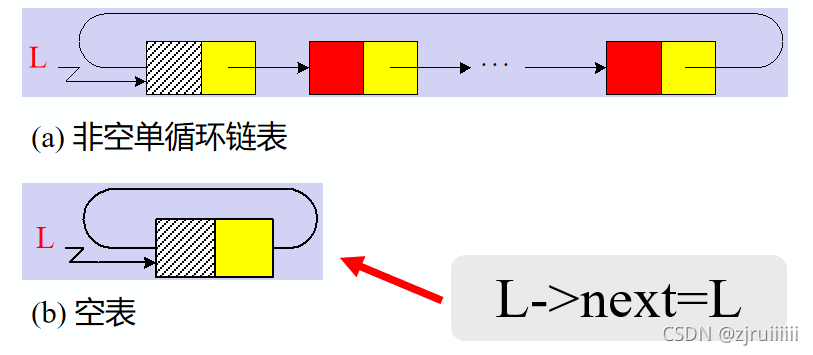
2.循环链表特点
从循环链表中的任何一个结点的位置都可以找到其他所有结点,而单链表做不到。
对循环链表,有时不给出头指针,而给出尾指针,可以更方便的找到第一个和最后一个结点。

3.循环链表的合并
首先设置一个指针指向第一个链表的头结点处,连接各个元素,连接完毕后去掉第二个链表的头结点,即完成循环链表的合并。
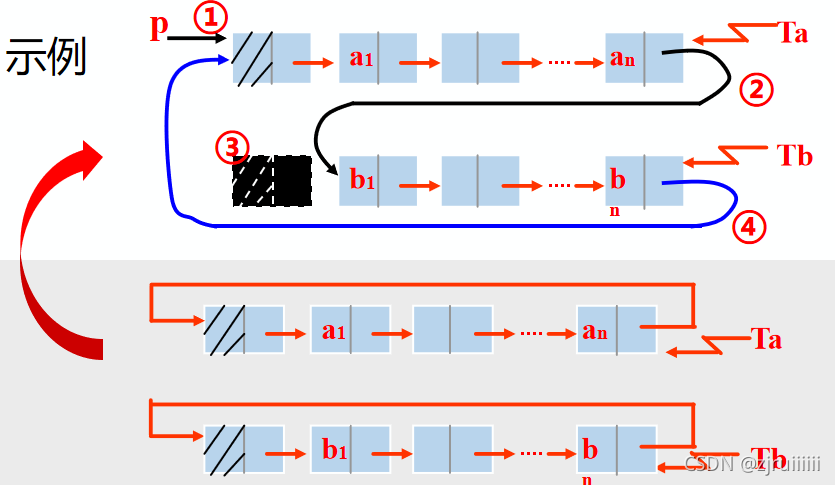
LinkList Connect(LinkList Ta,LinkList Tb)
{//假设Ta、Tb都是非空的单循环链表
p=Ta->next; //①p存表头结点
Ta->next=Tb->next->next;//②Tb表头连结Ta表尾
delete Tb->next; //③释放Tb表头结点
Tb->next=p; //④修改指针
return Tb;
}
七、双向链表
1.双向链表基本形态及特点
typedef struct DuLNode{
ElemType data;
struct DuLNode *prior;
struct DuLNode *next;
}DuLNode, *DuLinkList
双向链表除了数据域外,在其两端分别都是指针。
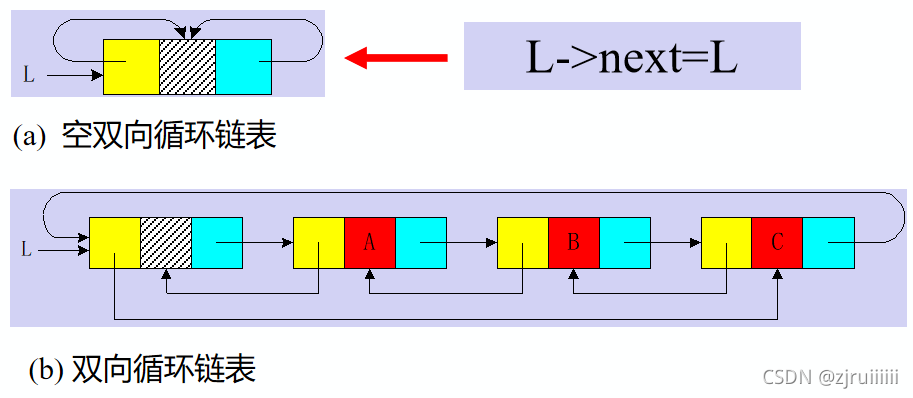
需要注意的是,双向链表有以下的特点:d->next->prior = d->prior->next = d。
2.双向链表的插入
双向链表插入的图示:
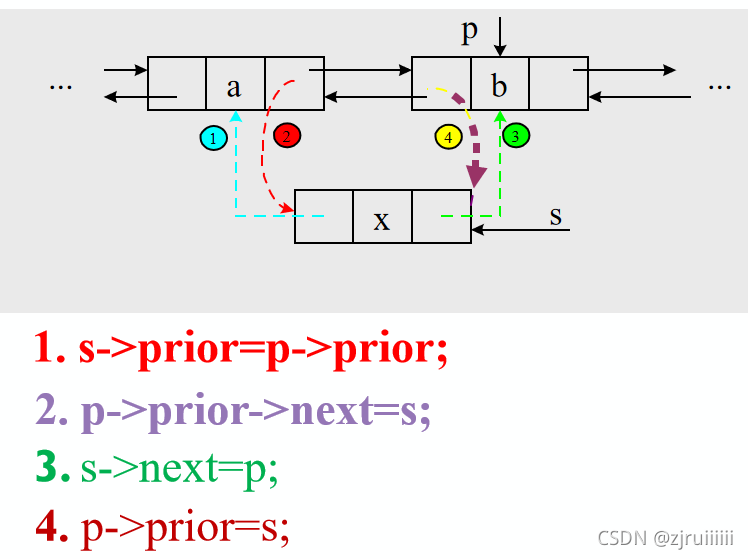
Status ListInsert_DuL(DuLinkList &L,int i,ElemType e){
if(!(p=GetElemP_DuL(L,i))) return ERROR;//查找第i个元素,在该元素前插入
s=new DuLNode;
s->data=e;
s->prior=p->prior;
p->prior->next=s;
s->next=p;
p->prior=s;
return OK;
}
3.双向链表的删除
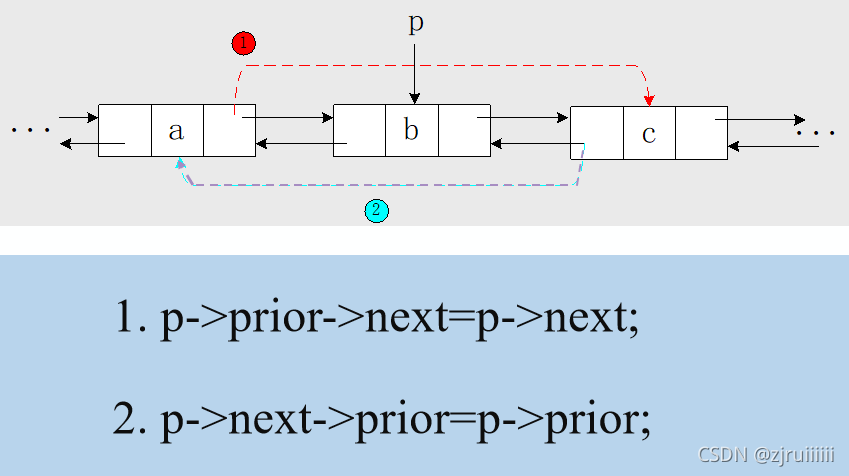
双向链表删除图示及关键步骤:
Status ListDelete_DuL(DuLinkList &L,int i,ElemType &e)
{
if(!(p=GetElemP_DuL(L,i))) return ERROR;
e=p->data;
p->prior->next=p->next;
p->next->prior=p->prior;
delete p;
return OK;
}
八、顺序表和链表的比较
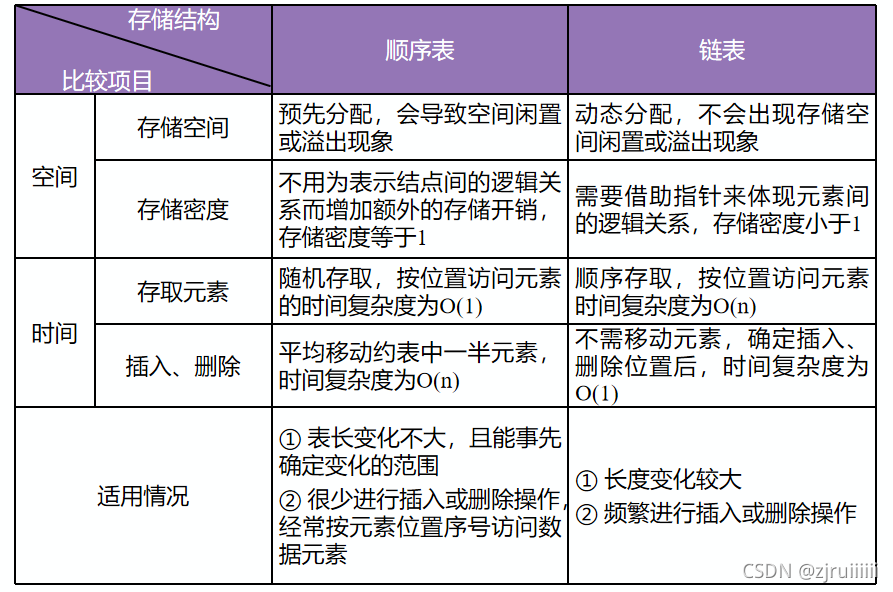
此表不需要记,理解即可。
九、线性表的应用
1.线性表的合并
问题描述:假设利用两个线性表La和Lb分别表示两个集合A和B,现要求一个新的集合。
算法步骤:
依次取出Lb 中的每个元素,执行以下操作。
1.在La中查找该元素。
2.如果找不到,则将其插入La的最后。
void union(List &La, List Lb){
La_len=ListLength(La);
Lb_len=ListLength(Lb);
for(i=1;i<=Lb_len;i++){
GetElem(Lb,i,e);
if(!LocateElem(La,e))
ListInsert(&La,++La_len,e);
}
}
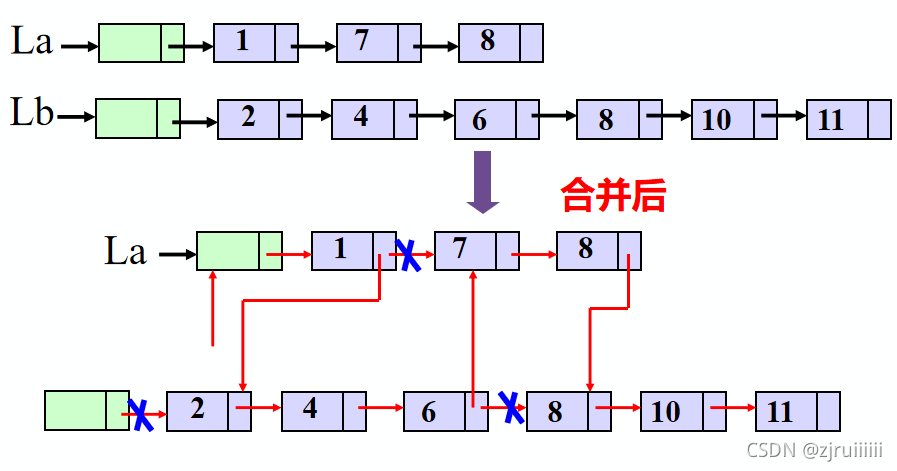
2. 顺序有序表的合并
问题描述:
已知线性表La 和Lb中的数据元素按值非递减有序排列,现要求将La和Lb归并为一个新的线性表Lc,且Lc中的数据元素仍按值非递减有序排列。(非递减排列不排除元素相等)
算法步骤:
1.创建一个空表Lc。
2.依次从 La 或 Lb 中“摘取”元素值较小的结点插入到 Lc 表的最后,直至其中一个表变空为止。
3.继续将 La 或 Lb 其中一个表的剩余结点插入在 Lc 表的最后。
void MergeList_Sq(SqList LA,SqList LB,SqList &LC){
pa=LA.elem; pb=LB.elem; //指针pa和pb的初值分别指向两个表的第一个元素
LC.length=LA.length+LB.length; //新表长度为待合并两表的长度之和
LC.elem=new ElemType[LC.length]; //为合并后的新表分配一个数组空间
pc=LC.elem; //指针pc指向新表的第一个元素
pa_last=LA.elem+LA.length-1; //指针pa_last指向LA表的最后一个元素
pb_last=LB.elem+LB.length-1; //指针pb_last指向LB表的最后一个元素
while(pa<=pa_last && pb<=pb_last){ //两个表都非空
if(*pa<=*pb) *pc++=*pa++; //依次“摘取”两表中值较小的结点
else *pc++=*pb++; } pa++; //LB表已到达表尾
while(pb<=pb_last) *pc+
while(pa<=pa_last) *pc++=*+=*pb++; //LA表已到达表尾
}//MergeList_Sq
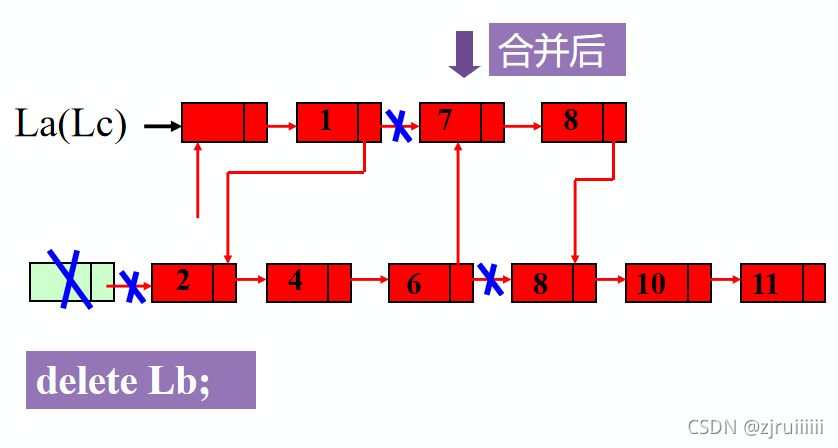
3.有序链表的合并
算法步骤:

合并后示意图:
void MergeList_L(LinkList &La,LinkList &Lb,LinkList &Lc){
pa=La->next; pb=Lb->next;
pc=Lc=La; //用La的头结点作为Lc的头结点
while(pa && pb){
if(pa->data<=pb->data){ pc->next=pa;pc=pa;pa=pa->next;}
else{pc->next=pb; pc=pb; pb=pb->next;}
pc->next=pa?pa:pb; //插入剩余段
delete Lb; //释放Lb的头结点}
总结:顺序有序表的合并与链式有序表的合并的时间复杂度都为O(m+n)。因为顺序有序表合并时需要开辟另一个存储空间,因此合并顺序有序表的空间复杂度为O(m+n),而合并链式有序表只需将前后地址修改即可,没有开辟新的存储空间,因此空间复杂度为0(1)。
十、案例实现与分析
1.多项式的创建
算法步骤:

void CreatePolyn(Polynomial &P,int n)
{//输入m项的系数和指数,建立表示多项式的有序链表P
P=new PNode;
P->next=NULL; //先建立一个带头结点的单链表
for(i=1;i<=n;++i) //依次输入n个非零项
{
s=new PNode; //生成新结点
cin>>s->coef>>s->expn; //输入系数和指数
pre=P; //pre用于保存q的前驱,初值为头结点
q=P->next; //q初始化,指向首元结点
while(q&&q->expn<s->expn) //找到第一个大于输入项指数的项*q
{
pre=q;
q=q->next;
}
s->next=q; //将输入项s插入到q和其前驱结点pre之间
pre->next=s;
}
}
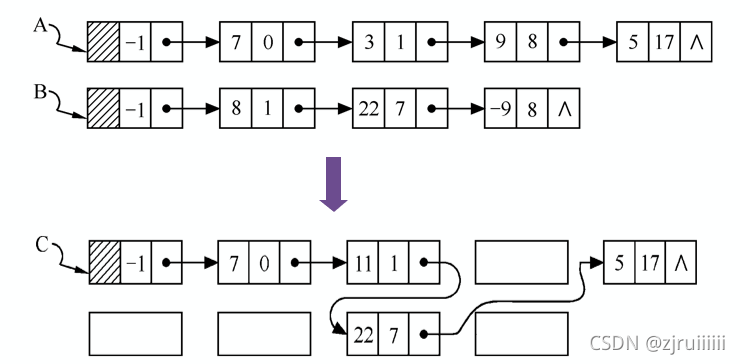
2.多项式的相加
多项式相加示意图:
多项式相加算法步骤:

书上有类C语言代码,因此这里不必重复。
假设两个多项式的项数分别为m和n,则算法的时间复杂度为O(m+n),空间复杂度为O(1)。
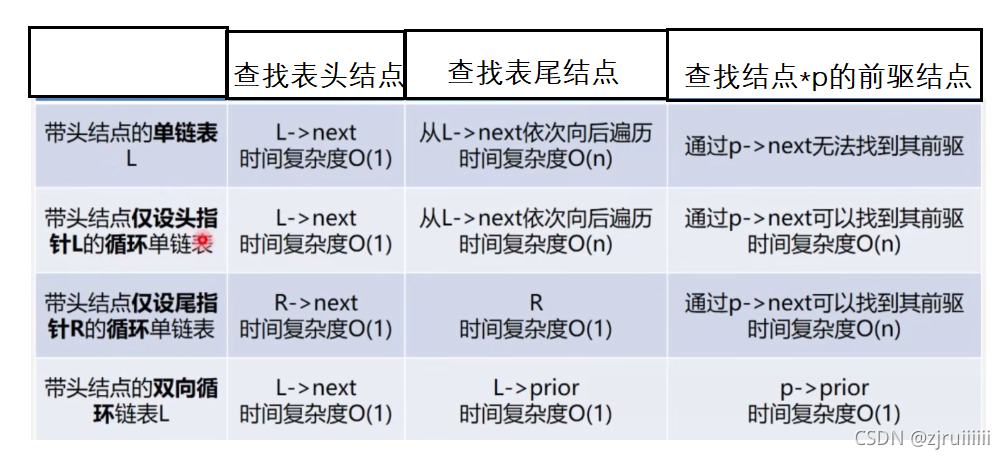
十一、单链表、循环链表、双向链表的时间效率的比较
十二、总结
-
掌握线性表的逻辑结构特性是数据元素之间存在着线性关系,在计算机中表示这种关系的两类不同的存储结构是顺序存储结构(顺序表)和链式存储结构(链表)。
-
熟练掌握这两类存储结构的描述方法,掌握链表中的头结点、头指针和首元结点的区别及循环链表、双向链表的特点等。
-
熟练掌握顺序表的查找、插入和删除算法 。
-
能够从时间和空间复杂度的角度比较两种存储结构的不同特点及其适用场合 。
原创不易,如果此篇文章对您了解数据结构的线性表有帮助,麻烦点个赞支持一下谢谢。