目录
1. 问题描述
2. 解题分析
2.1 DFS算法流程
2.2 遍历下一个状态
3. 代码及测试
4. 后记
1. 问题描述
对喜爱棒球的少年而言,“三振出局”是一定要试一次的。这是一个在本垒上放置 9 个靶子,击打投手投来的球,命中靶子的游戏。据说这可以磨练球手的控制力。
现在来思考一下这 9 个靶子的击打顺序。假设除了高亮的 5 号靶子以外,如果1个靶子有相邻的靶子,则可以一次性把这 2 个靶子都击落。譬如,如图2所示,假设 1 号、6 号、9 号已经被击落了,
那么接下来,对于 “2和3” “4和7” “7和8” 这3组靶子,我们就可以分别一次性击落了。
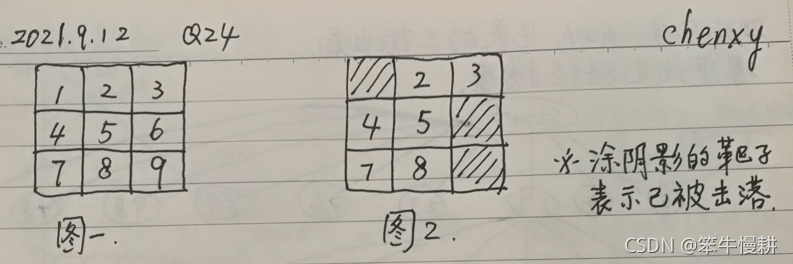
求:9 个靶子的击落顺序有多少种?这里假设每次投手投球后,击球手都可以击中靶子。
2. 解题分析
第一感就是深度优先路径搜索问题。因为本系列已经出现来太多这样的问题,比如Q23, Q18, Q14, just to name a few.
2.1 DFS算法流程
由于已经击落的靶子就不能再用了,所以靶盘状态用尚未被击落的靶子的列表表示即可。

2.2 遍历下一个状态
深度优先搜索的同一类问题都可以直接套用上一节所示的框架套路,除了一些problem-specific的细节需要针对个别问题具体处理。本问题的要点在于如何给出下一个状态的遍历列表来。
本题解采用(比较笨拙的)办法如下:
首先,定义一个查找表,包括所有可能的double-strike(一次击落两块)的可能组合。
其次,搜索当前的unStriked的2-combination’s,并查找各自是否出现在double-strike列表中,如果在的话则表明这是一种可能的double-strike结果,由此导致一种next-state
最后,所有unStriked的中靶子都可能被单独击落,也分别导致一种next-state
代码参见findNext(unStriked)
3. 代码及测试
# -*- coding: utf-8 -*-
"""
Created on Sun Sep 12 08:49:46 2021
@author: chenxy
"""
import sys
import time
import datetime
import math
# import random
from typing import List
# from queue import Queue
# from collections import deque
import itertools as it
double_strike = [{1,2},{1,4},{2,3},{3,6},{6,9},{8,9},{7,8},{4,7}]
class Solution:
def baseball_game(self, unStriked: List)->int:
"""
Parameters
----------
Returns : The number of order of striking
-------
"""
memo = dict()
def findNext(unStriked):
global double_strike
ansLst = []
strike2Lst= []
# Search for all possible double strikes
for item in it.combinations(unStriked, 2):
# print(item)
if set(item) in double_strike:
new = unStriked.copy()
new.remove(item[0])
new.remove(item[1])
ansLst.append(new)
strike2Lst.append(item)
# Search for all possible single strikes
for num in unStriked:
new = unStriked.copy()
new.remove(num)
ansLst.append(new)
# print('findNext: {0}-->{1}'.format(unStriked,ansLst))
return ansLst
def explore(unStriked):
"""
unStriked : The list of targets not yet striked
Returns : The number of order of striking
-------
"""
# print(unStriked)
if len(unStriked) == 0:
return 1
if tuple(unStriked) in memo:
return memo[tuple(unStriked)]
count = 0
nextUnStriked = findNext(unStriked)
for item in nextUnStriked:
count = count + explore(item)
memo[tuple(unStriked)] = count
return count
return explore(unStriked)
if __name__ == '__main__':
sln = Solution()
tStart = time.perf_counter()
count = sln.baseball_game([k for k in range(1,10)])
tCost = time.perf_counter() - tStart
print('count = {0}, tCost = {1:6.3f}(sec)'.format(count,tCost)) 运行结果:count = 798000, tCost = 0.004(sec)
4. 后记
本题说明其实是有一定模糊性(因为我一开始恰好掉到坑里去了)的。在关于一次能击落两块的情况中,题意其实是说当除了5以外,任意两块连着的靶子,击中其中任意一块时可能只掉下被击落的那一块,也可能把相邻的那一块带下去(但是两边都有相邻靶子的话,也只会带下一块)。这对应着实际的游戏情况应该是球正好几种两个靶子的交界处附近,对于实际玩过棒球或者观看过类似电视节目的人来说可能是理所当然的,但是作为一道抽象的算法题目来说则很难说是理所当然的。
既然说到这儿,这道题目可以稍微做一下条件修改:任意两块连着的靶子,击中其中任意一块时一定会连同相邻的那一块一起掉下去(两边都有相邻靶子的话,也只会带下其中某一块)。在这种条件下,9个靶子的击落顺序有多少种呢?
嗯,这道延申题目算不算有点原创的意思?^-^
上一篇:Q23: 二十一点通吃
下一篇:Q27: 禁止右转
本系列总目录参见:程序员的算法趣题:详细分析和Python全解