2021高教社杯全国大学生数学建模
B 题 乙醇偶合制备 C4 烯烃
C4 烯烃广泛应用于化工产品及医药的生产,乙醇是生产制备 C4 烯烃的原料。在制备过程中,催化剂组合(即:Co 负载量、Co/SiO2 和 HAP 装料比、乙醇浓度的组合)与温度对 C4 烯烃的选择性和 C4 烯烃收率将产生影响(名词解释见附录)。
因此通过对催化剂组合设计,探索乙醇催化偶合制备 C4 烯烃的工艺条件具有非常重要的意义和价值。
某化工实验室针对不同催化剂在不同温度下做了一系列实验,结果如附件 1 和附件 2 所示。请通过数学建模完成下列问题:
(1) 对附件 1 中每种催化剂组合,分别研究乙醇转化率、C4 烯烃的选择性与温度的关系,并对附件 2 中 350 度时给定的催化剂组合在一次实验不同时间的测试结果进行分析。
(2) 探讨不同催化剂组合及温度对乙醇转化率以及 C4 烯烃选择性大小的影响。
(3) 如何选择催化剂组合与温度,使得在相同实验条件下 C4 烯烃收率尽可能高。若使温度低于 350 度,又如何选择催化剂组合与温度,使得 C4 烯烃收率尽可能高。
(4) 如果允许再增加 5 次实验,应如何设计,并给出详细理由。
问题一程序代码:
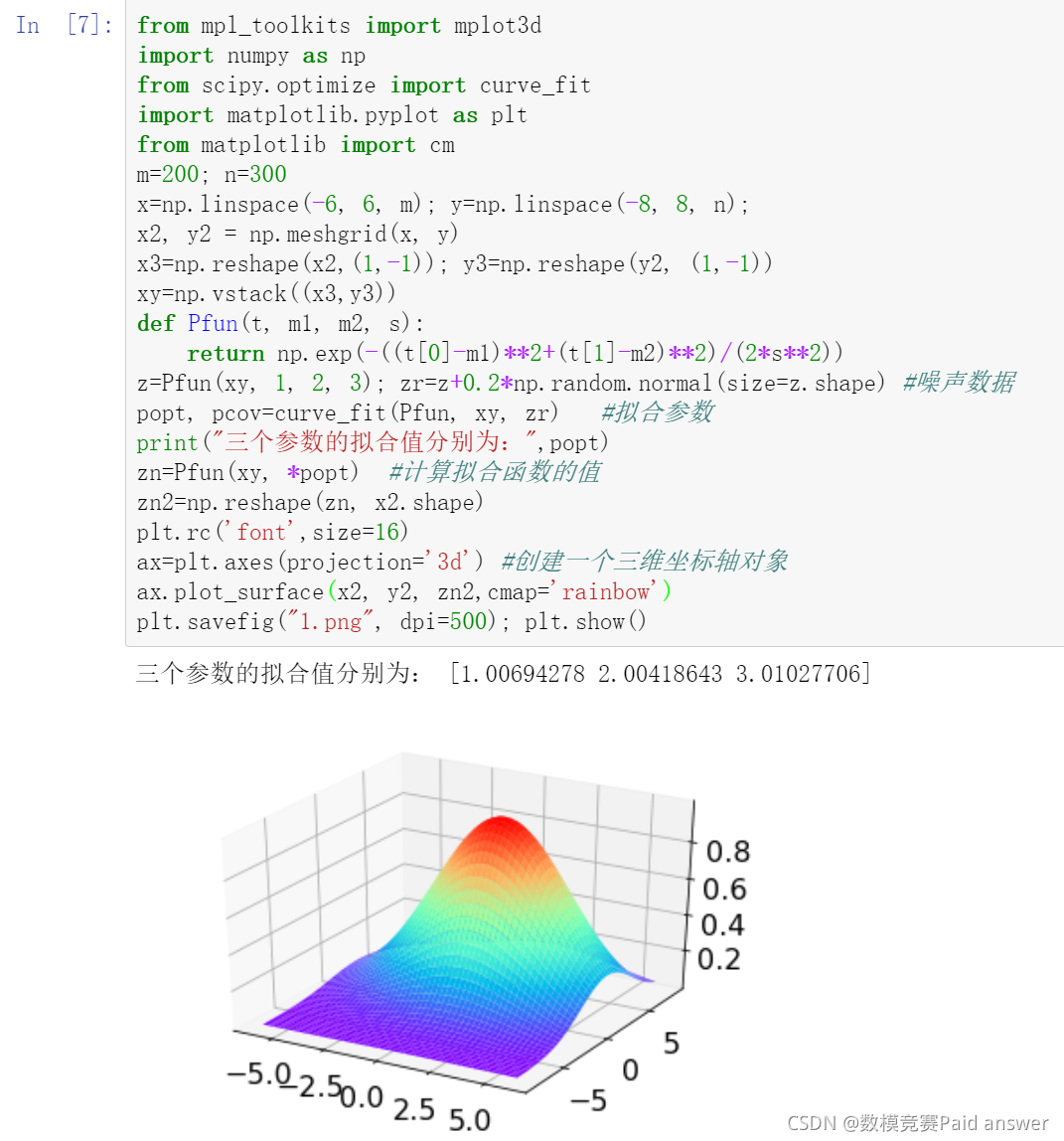
from mpl_toolkits import mplot3d
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
m=200; n=300
x=np.linspace(-6, 6, m); y=np.linspace(-8, 8, n);
x2, y2 = np.meshgrid(x, y)
x3=np.reshape(x2,(1,-1)); y3=np.reshape(y2, (1,-1))
xy=np.vstack((x3,y3))
def Pfun(t, m1, m2, s):
return np.exp(-((t[0]-m1)**2+(t[1]-m2)**2)/(2*s**2))
z=Pfun(xy, 1, 2, 3); zr=z+0.2*np.random.normal(size=z.shape) #噪声数据
popt, pcov=curve_fit(Pfun, xy, zr) #拟合参数
print("三个参数的拟合值分别为:",popt)
zn=Pfun(xy, *popt) #计算拟合函数的值
zn2=np.reshape(zn, x2.shape)
plt.rc('font',size=16)
ax=plt.axes(projection='3d') #创建一个三维坐标轴对象
ax.plot_surface(x2, y2, zn2,cmap='gist_rainbow')
plt.savefig("figure7_10.png", dpi=500); plt.show()
import matplotlib.pyplot as plt
"""
@brief: 计算n阶差商 f[x0, x1, x2 ... xn]
@param: xi 所有插值节点的横坐标集合 o
@param: fi 所有插值节点的纵坐标集合 / \
@return: 返回xi的i阶差商(i为xi长度减1) o o
@notice: a. 必须确保xi与fi长度相等 / \ / \
b. 由于用到了递归,所以留意不要爆栈了. o o o o
c. 递归减递归(每层递归包含两个递归函数), 每层递归次数呈二次幂增长,总次数是一个满二叉树的所有节点数量(所以极易栈溢出)
"""
def diff_quo(xi = [], fi = []):
if len(xi) > 2 and len(fi) > 2:
return (diff_quo(xi[:len(xi) - 1], fi[:len(fi) - 1]) - diff_quo(xi[1:len(xi)], fi[1:len(fi)])) / float(xi[0] - xi[-1])
return (fi[0] - fi[1]) / float(xi[0] - xi[1])
"""
@brief: 获得Wi(x)函数;
Wi的含义举例 W1 = (x - x0); W2 = (x - x0)(x - x1); W3 = (x - x0)(x - x1)(x - x2)
@param: i i阶(i次多项式)
@param: xi 所有插值节点的横坐标集合
@return: 返回Wi(x)函数
"""
def get_Wi(i = 0, xi = []):
def Wi(x):
result = 1.0
for each in range(i):
result *= (x - xi[each])
return result
return Wi
"""
@brief: 获得牛顿插值函数
@
"""
def get_Newton_inter(xi = [], fi = []):
def Newton_inter(x):
result = fi[0]
for i in range(2, len(xi)):
result += (diff_quo(xi[:i], fi[:i]) * get_Wi(i-1, xi)(x))
return result
return Newton_inter
"""
demo:
"""
if __name__ == '__main__':
''' 插值节点, 这里用二次函数生成插值节点,每两个节点x轴距离位10 '''
sr_x = [i for i in range(-50, 51, 10)]
sr_fx = [i**2 for i in sr_x]
Nx = get_Newton_inter(sr_x, sr_fx) # 获得插值函数
tmp_x = [i for i in range(-50, 51)] # 测试用例
tmp_y = [Nx(i) for i in tmp_x] # 根据插值函数获得测试用例的纵坐标
''' 画图 '''
plt.figure("aaa")
ax1 = plt.subplot(111)
plt.sca(ax1)
plt.plot(sr_x, sr_fx, linestyle = '', marker='o', color='b')
plt.plot(tmp_x, tmp_y, linestyle = '--', color='r')
plt.show()


解题关键
print("联系qq:3506426881")