B+树真的不难，楼下菜大爷都能学得会的B+树！（数据结构可视化神器推荐）_菜菜bu菜的博客

💕前言💕

楼下菜大爷遛弯的时候经常在菜菜身边装逼，说什么b+树很简单
你们觉得我信吗？信吗？可是…
当菜菜把这篇文章认认真真的看完之后!!!

被他装到了，可恶！！！不信？看完评论区见

✨b树家族、一个都别想跑✨

讲b+树前，先调查一下它的血亲！一个都别想跑！来来来，给我排整齐给大家看看~

B树、B-树（嫌疑较大，留意）、B+树、B*树

一个普普通通的树（二叉树），非要搞这么多玩意，区别是啥：

姓名（术语）	简介
B树	多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点；所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；
B-树	就是B树（没想到吧）
B+树	在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；
B*树	在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3；

秘闻;

• 因为B树的原英文名称为B-tree，而国内很多人喜欢把B-tree译作B-树,所以人们可能会以为B-树是一种树，而B树又是另一种树。而事实上是，B-tree就是指的B树。

💙前提条件，温故而知新💙

💨什么是AVL树❓

• 平衡二叉树，一般是用平衡因子差值决定并通过旋转来实现，左右子树树高差不超过1，那么和红黑树比较它是严格的平衡二叉树，平衡条件非常严格（树高差只有1），只要插入或删除不满足上面的条件就要通过旋转来保持平衡。由于旋转是非常耗费时间的。我们可以推出AVL树适合用于插入删除次数比较少，但查找多的情况。

💨什么是红黑树❓

• 平衡二叉树，通过对任何一条从根到叶子的简单路径上各个节点的颜色进行约束，确保没有一条路径会比其他路径长2倍，因而是近似平衡的。所以相对于严格要求平衡的AVL树来说，它的旋转保持平衡次数较少。用于搜索时，插入删除次数多的情况下我们就用红黑树来取代AVL。

💨什么是二叉搜索树❓

举个例子，二叉搜索树来作为索引的案例：

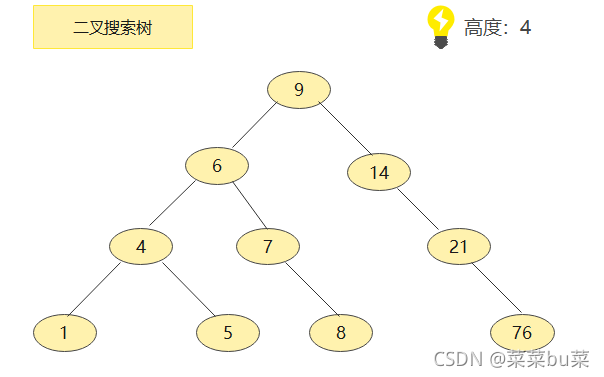
现在来查找节点为5的节点，来看看需要几步：

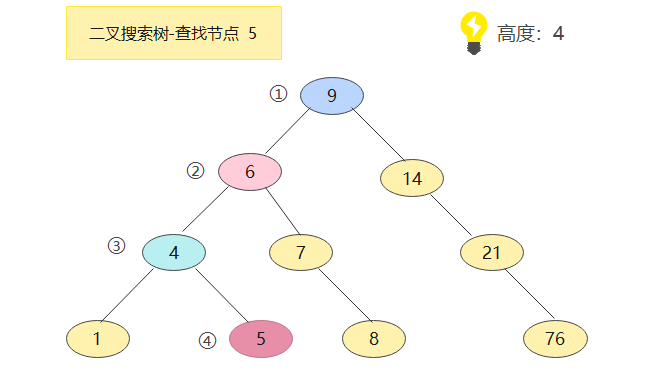
没错，一共四步，但是要注意，一般索引是在内存中执行的，所以价格很昂贵！！在最坏的情况下磁盘读写次数==二叉搜索树的高度，这在实际应用中肯定是不行的，所以基于此，诞生了B树*（多路平衡树）来减少数的高度，那么🔻

💨什么是B树（多路平衡树）❓

B树其实最开始源于的是二叉树，二叉树是只有左右孩子的树，当数据量越大的时候，二叉树的节点越多，那么当从根节点搜索的时候，影响查询效率。所以如果这些节点存储在外存储器中的话，每访问一个节点，相当于进行了一次I/O操作。前面说过，为了减少磁盘的 I/O 操作才有的B树，那么来看下B树有什么特点：

还是上面那个问题，来看下B树怎么个解决方案：

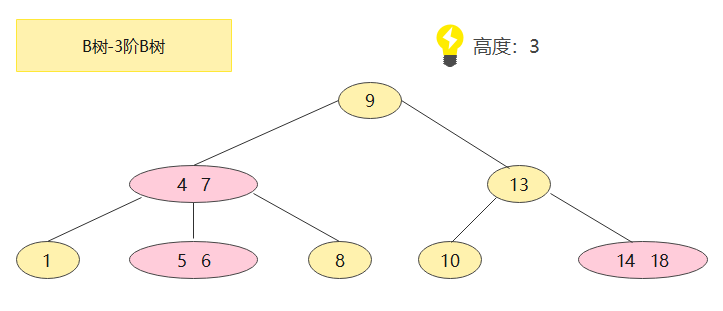
ps：K被称为B树的阶，K的值取决于磁盘页（内存的最小存储单位）的大小

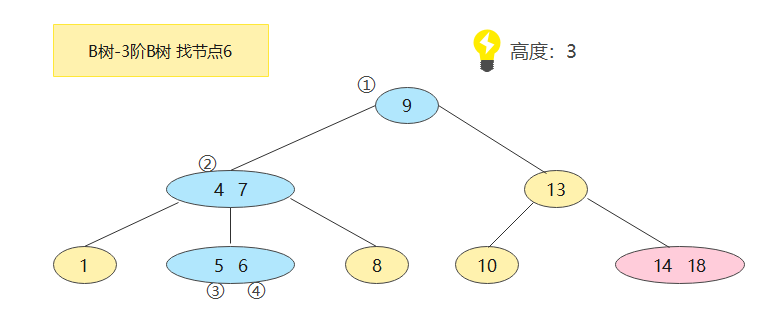
假设搜索节点6，步骤：

• ①定位到根节点（9），6比9小，所以在左子树找
• ②定位到节点（4，7），6在4、7中间，所以在中间子树找
• ③定位到（5，6），6比5大，所以和该节点的右边比较
• ④找到，over

可以看出，在B树里面的比较次数也很多，但是❗减少了I/O操作，因为B树可以减少树的高度，也就减少了磁盘读写次数，在实际应用场景，B树对性能的提升非常明显。

最后，大家可能之前都知道B树的特点，现在应该会更好理解：

• 1.根结点至少有两个子节点。
• 2.每个中间节点都包含k-1个元素和k个孩子，其中 m/2 <= k <= m 。
• 3.每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m。
• 4.所有的叶子结点都位于同一层。
• 5.每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划。

🧡b+树到底是啥玩意？就这？🧡

前面说了这么多，到这里才步入主题，先来调查一下…

经过菜菜调查发现，B+树的出现带来了这些优点：

1）B+树的磁盘读写代价更低

B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B
树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了；

2）B+树查询效率更加稳定

由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当；

3）B+树便于范围查询（最重要的原因，范围查找是数据库的常态）

B树在提高了IO性能的同时并没有解决元素遍历的我效率低下的问题，正是为了解决这个问题，B+树应用而生。B+树只需要去遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的，而B树不支持这样的操作或者说效率太低；

B+树最大的性能问题在于会产生大量的随机IO，主要存在以下两种缺点：

• 主键不是有序递增的，导致每次插入数据产生大量的数据迁移和空间碎片；
• 即使主键是有序递增的，大量写请求的分布仍是随机的；

看下B+树长什么样子

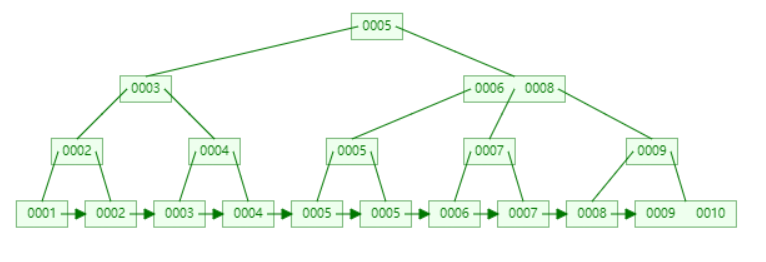
如果要查找0007的话，查找方式如下

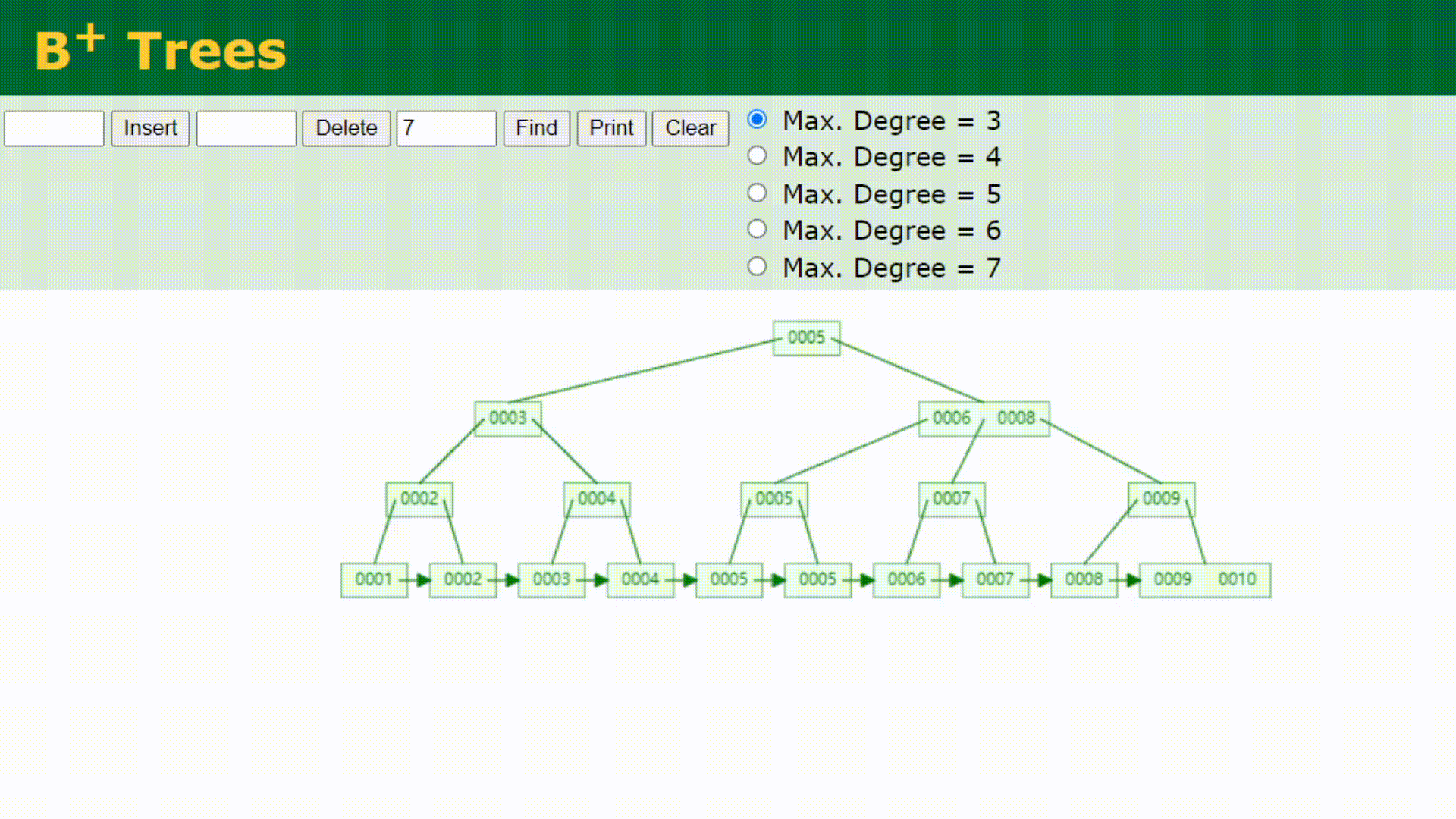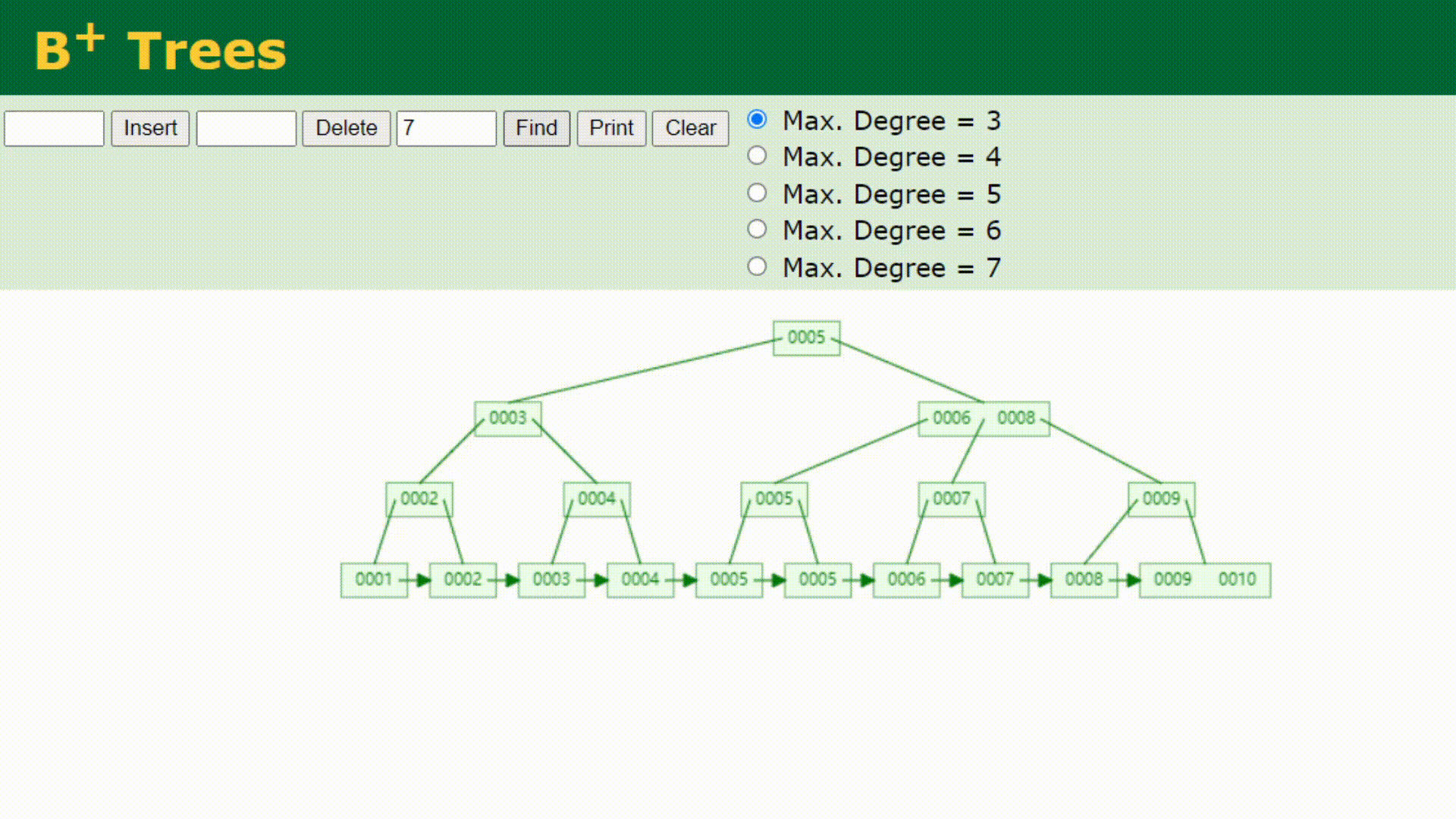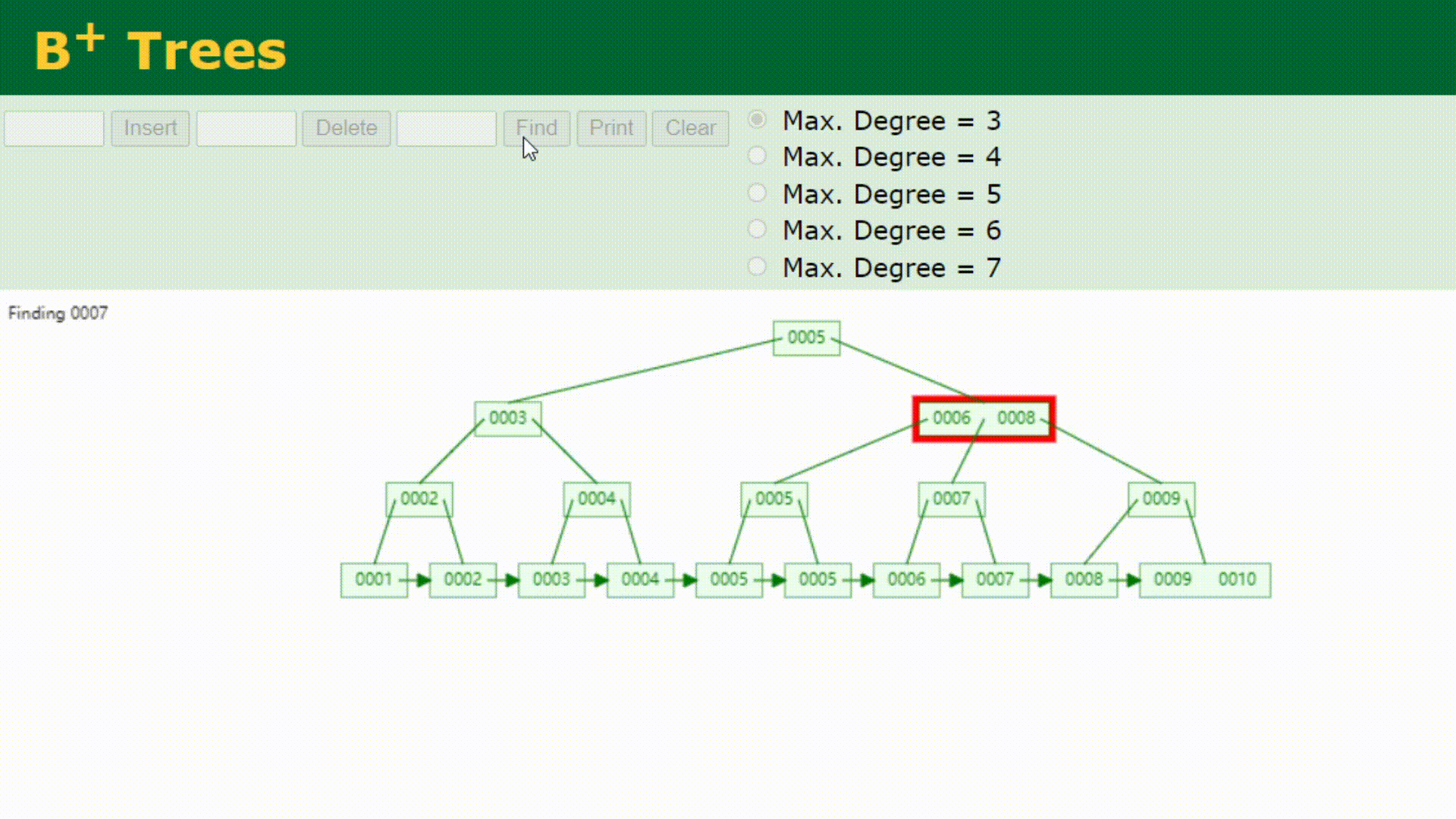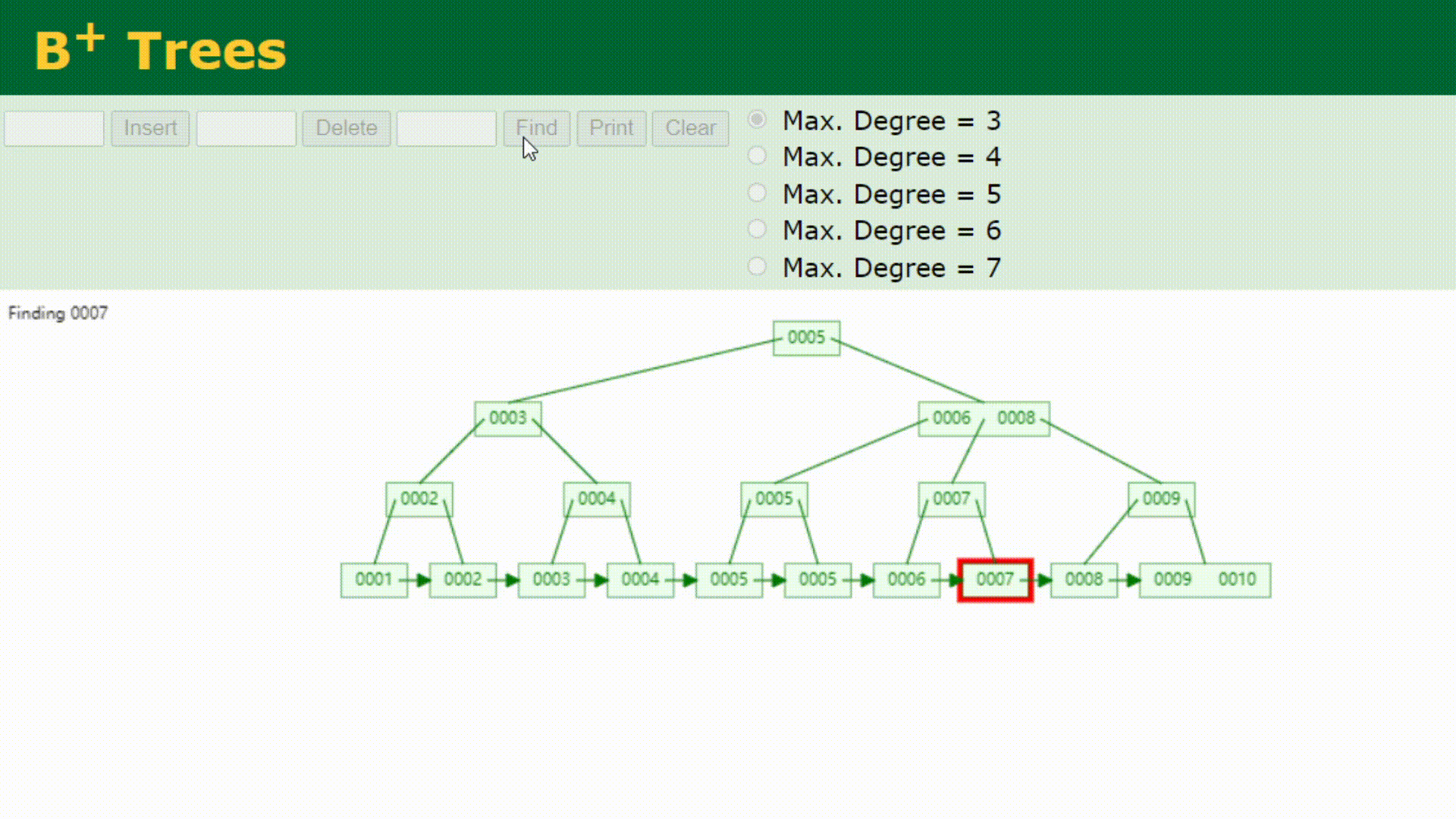
并且，为什么MySQL数据库索引选择使用B+树？
B+树的节点只存储索引key值，具体信息的地址存在于叶子节点的地址中。这就使以页为单位的索引中可以存放更多的节点。减少更多的I/O支出。因此，B+树成为了数据库比较优秀的数据结构，MySQL中MyIsAM和InnoDB都是采用的B+树结构。不同的是前者是非聚集索引，后者主键是聚集索引。

看下B+树的顺序查找：

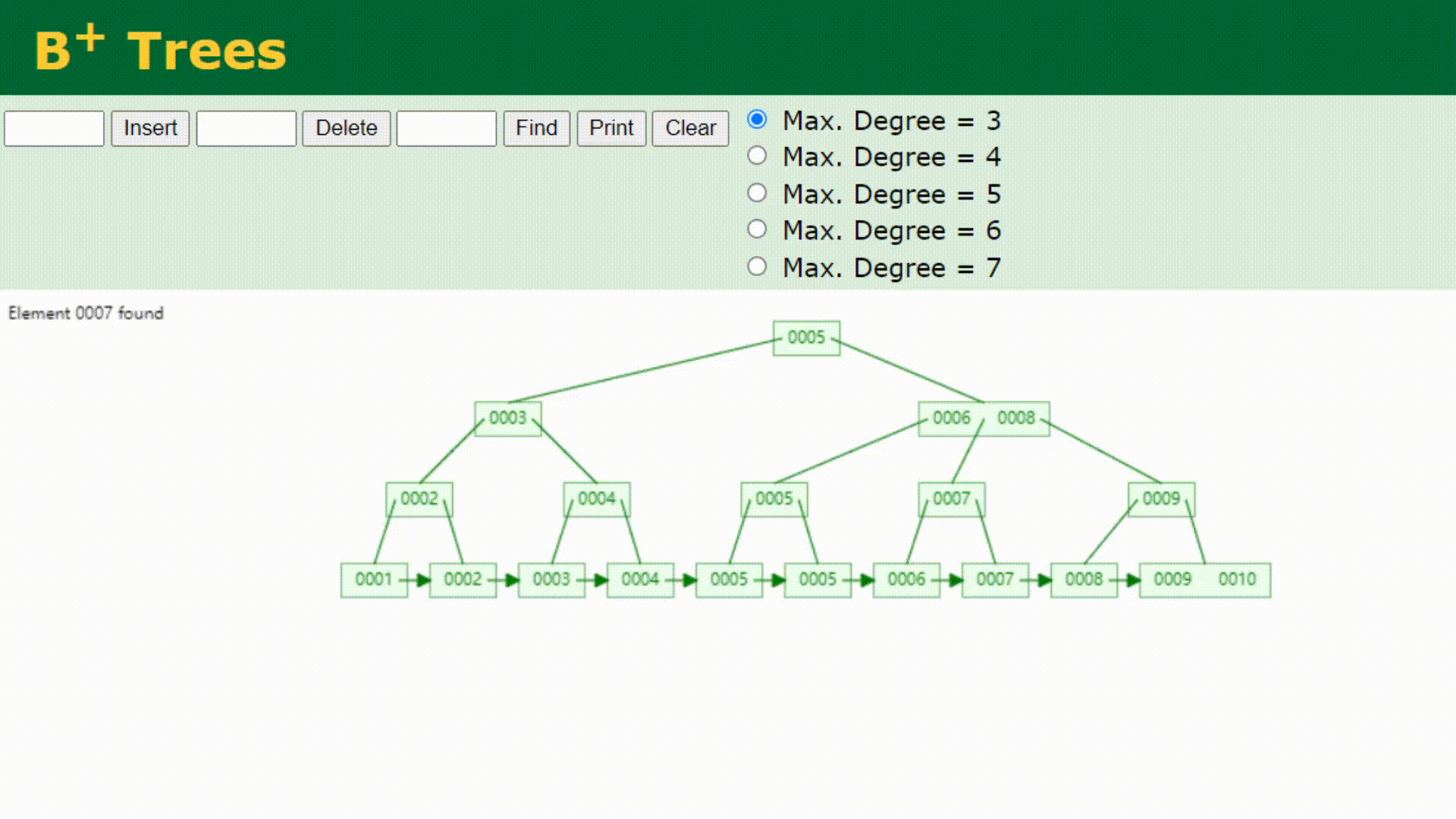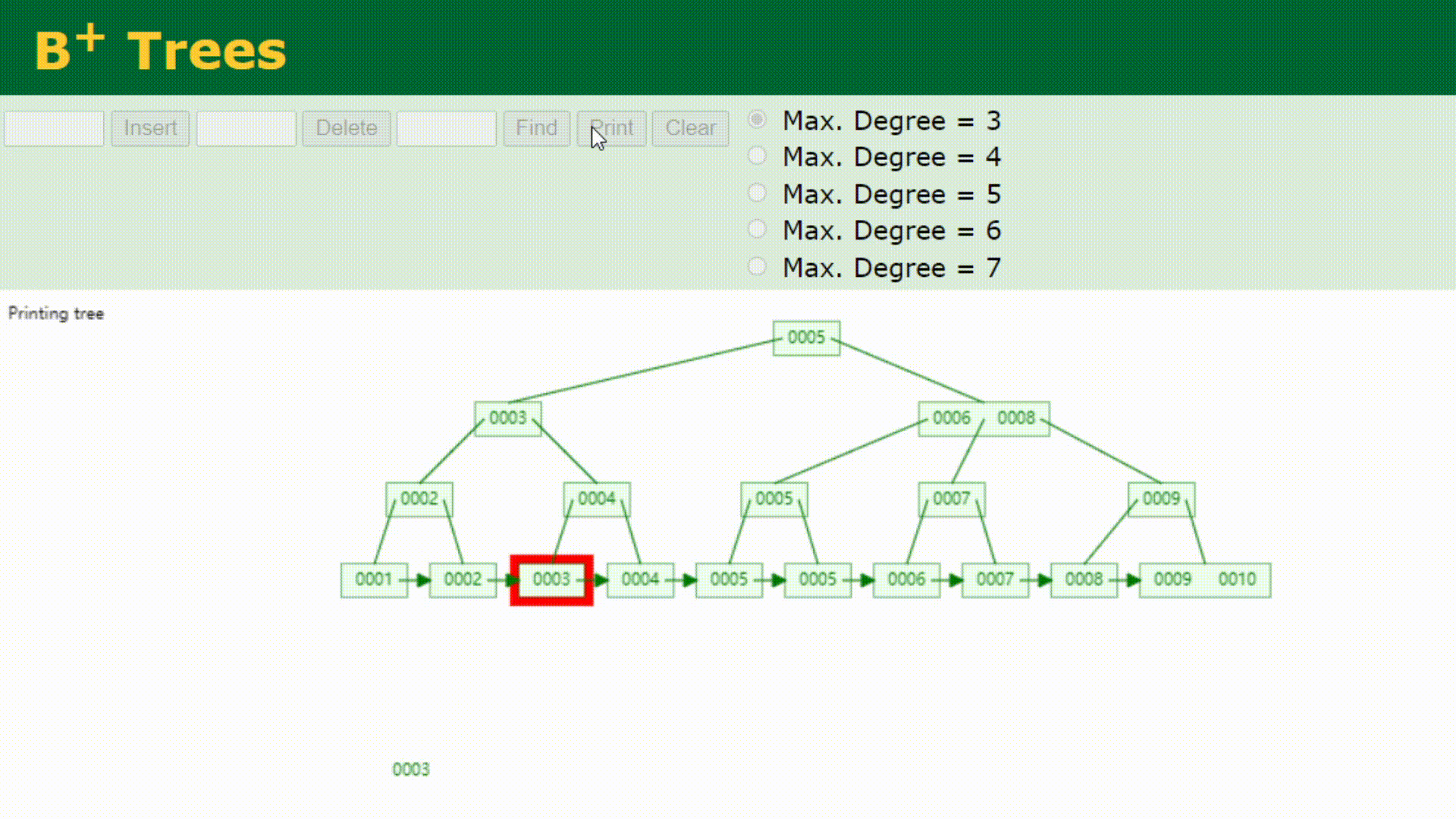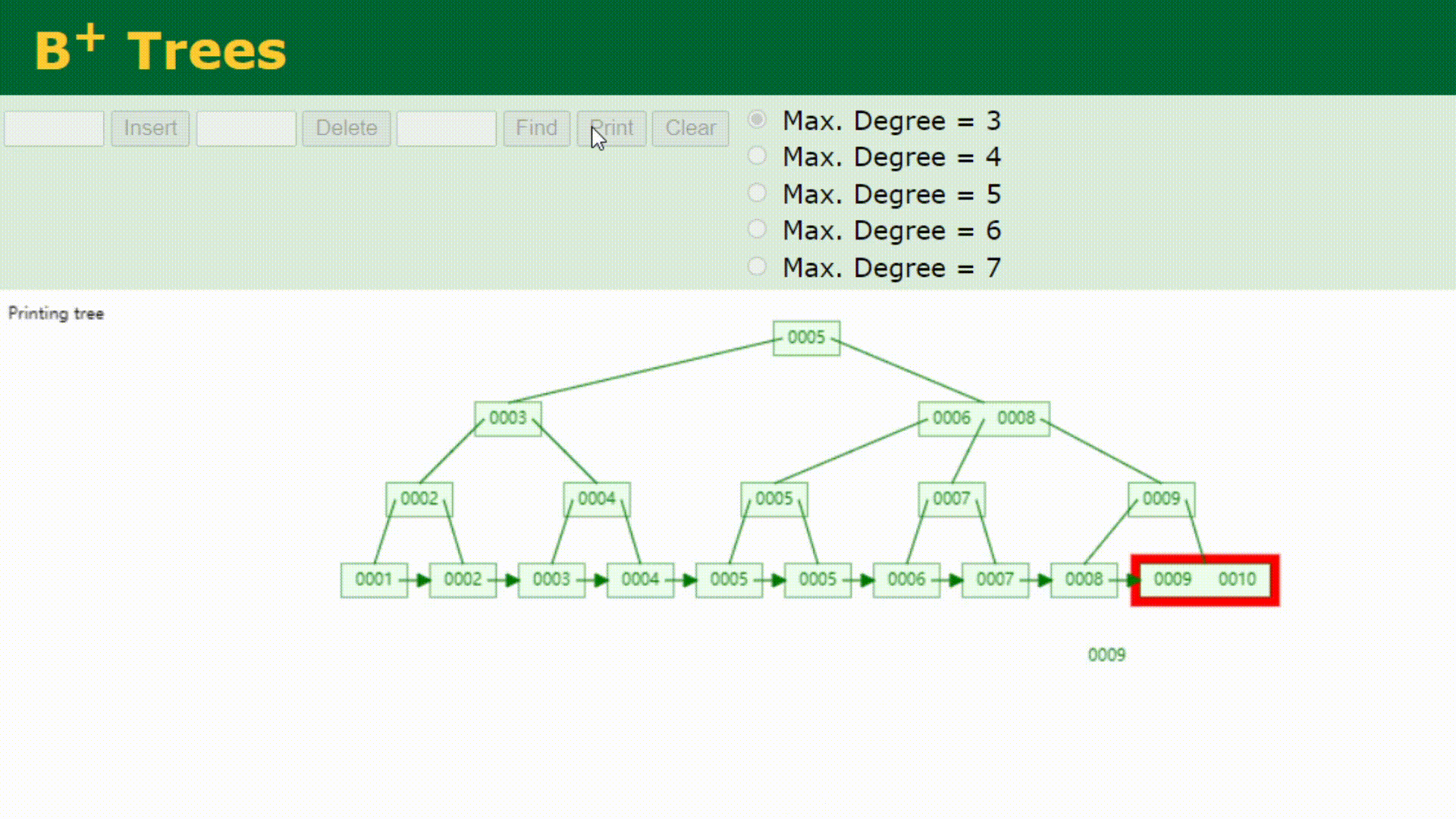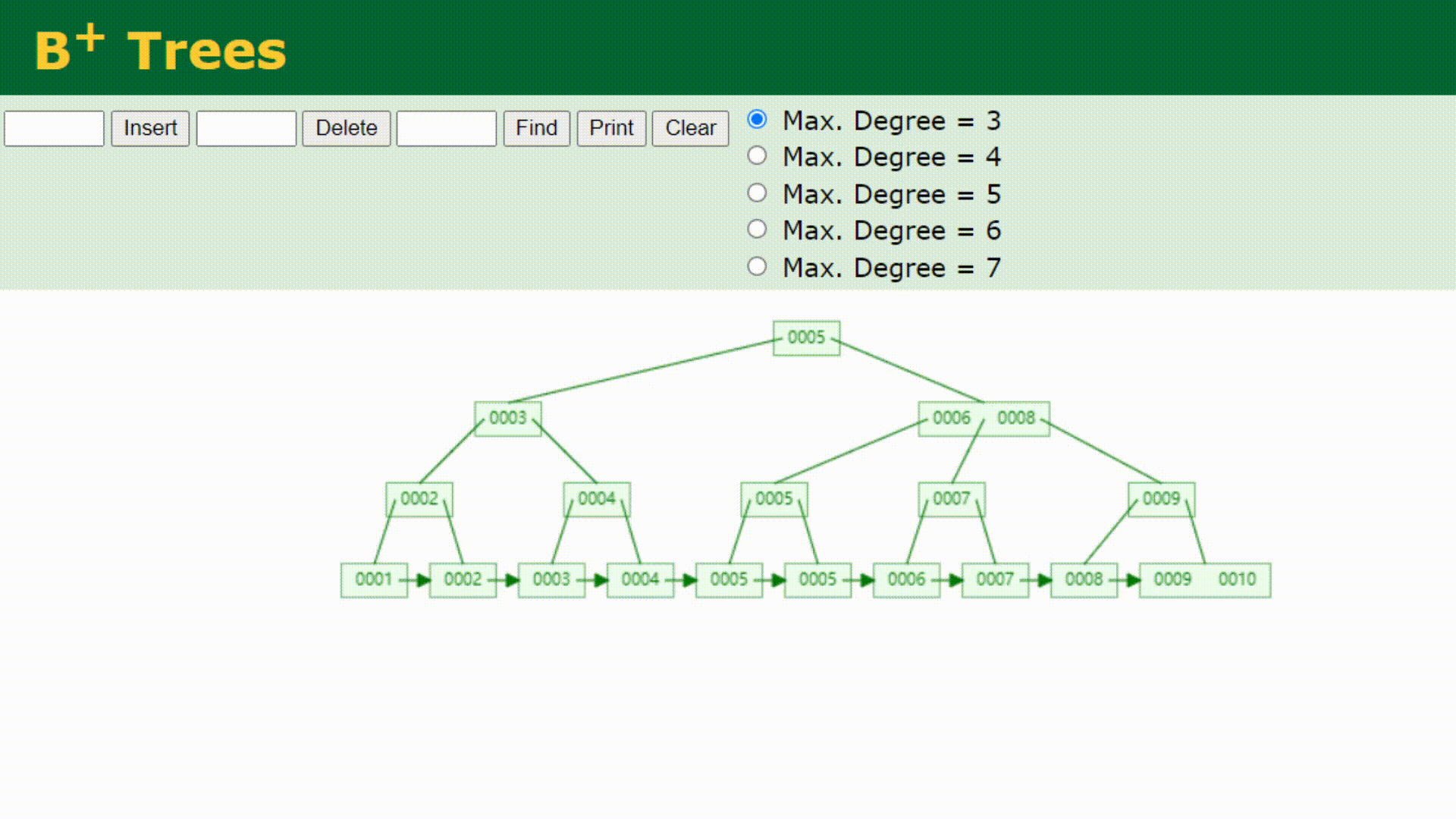
B树在提高了IO性能的同时并没有解决元素遍历的我效率低下的问题，正是为了解决这个问题，B+树应用而生。B+树只需要去遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的，而B树不支持这样的操作或者说效率太低。B+树支持range-query(区间查询)非常方便，而B树不支持。

B+ 树通常用于数据库和操作系统的文件系统中。

NTFS, ReiserFS, NSS, XFS, JFS, ReFS 和BFS等文件系统都在使用B+树作为元数据索引。B+ 树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。B+ 树元素自底向上插入。

💚B树、B+树都知道了，B*树不了解一下？💚

先看下百度的回答：

B树是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针；B树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3（代替B+树的1/2）。

B*树是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针：
找的网图（大佬莫怪）

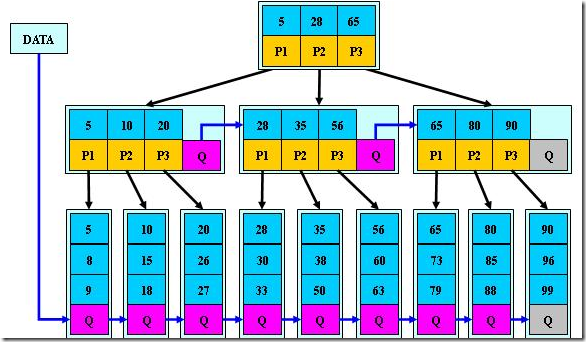
B+树和B*树的区别是啥？

• B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针；

• B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针；

可以看出，B*树分配新结点的概率比B+树要低，空间使用率更高；

💜数据库索引数据结构了解下？💜

MySql索引数据结构(BTREE和Hash)，也来简单了解下 BTREE和Hash的区别：

• 1、Hash 索引，其检索效率非常高，索引的检索可以一次定位。BTREE 索引需要从根节点到枝节点，最后才能访问到页节点这样多次的IO访问
• 2、Hash 索引仅仅能满足"=",“IN"和”<=>"查询，不能使用范围查询。
• 3、Hash 索引无法被用来避免数据的排序操作
• 4、Hash 索引不能利用部分索引键查询。
• 5、Hash 索引在任何时候都不能避免表扫描。
• 6、Hash 索引遇到大量Hash值相等的情况后性能并不一定就会比B-Tree索引高

而数据库一般采用B+树索引是因为Hash索引的话，不适合做范围查询，因为原先是有序的键值，经过哈希算法后，有可能变成不连续的了（比如原来Hello和World原来是在一起的，但是经过hash算法后就变成了0001 和1522）

索引 / 存储引擎	MyISAM	InnoDB	Memory
B-Tree索引	支持	支持	支持
HASH索引	不支持	不支持	支持
R-Tree索引	支持	支持	不支持
Full-text索引	支持	支持	不支持

hash索引的适用情况：
检索时不需要类似B+树那样从根节点到叶子节点逐级查找，只需一次哈希算法即可立刻定位到相应的位置，速度非常快。除了memory引擎外，NDB引擎也支持唯一哈希索引；

💛B+树代码实现💛

有缘相见🧡

🤎数据结构可视化神器推荐！🤎

旧金山大学做的 BPlusTree Visualization 模型数据结构可视化


一个字，绝！！！好用 好用 学起来~