👋Hi~ o(￣▽￣)ブ这里是猪猪程序员
👀 很高兴见到你O(∩_∩)O！
🌱 现在正在发芽中…
💞️ 博主水平有限，如果发现错误，一定要及时告知作者哦 o(￣︶￣)o！感谢感谢！
📫博主的码云 gitee，平常博主写的程序代码都在里面。

⭐️这是一个新的专栏⭐️我希望自己能够坚持把《剑指offer》这本书的题目刷完。

⭐️题目来源
实现 pow(x, n) ，即计算 x 的 n 次幂函数（即， x^n）。不得使用库函数，同时不需要考虑大数问题。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

-100.0 < x < 100.0
-231 <= n <= 231-1
-104 <= xn <= 104

方法一:直接求解（超出时间限制）

最简单的方法就是让n个x相乘，但这样会超出时间限制,而且我写的很冗余—！！！！

double myPow(double x, int n){
    double t = 1.0; int i = n;
    if (x > 0)
    {
        if (n > 0)
        {
            for (i = 0; i < n; i++)
            {
                t *= x;
            }
        }
        else if (n == 0)
        {
            t = 1;
        }
        else
        {
            for (i = 0; i < -n; i++)
            {
                t /= x;
            }
        }
    }
    else if (x == 0)
    {
        t = 0;
    }
    else
    {
        if (n > 0)
        {
            for (i = 0; i < n; i++)
            {
                t *= x;
            }
        }
        else if (n == 0)
        {
            t = 1;
        }
        else
        {
            for (i = 0; i < -n; i++)
            {
                t /= x;
            }
        }
    }
    return t;
}

方法二:使用递归（执行用时：0 ms 内存消耗：5.3 MB）

算法

算法流程：

1. n=0时，任何x都返回1
2. n=1时，返回x
3. n=-1时，返回1/x
4. 对于其他n值：
   1.1 当n为偶数时，myPow(x,n) = myPow(x,n/2)* myPow(x,n/2)
   1.2 当n为奇数时：myPow(x,n) = myPow(x,(n-1)/2) * myPow(x,(n-1)/2) * x
   递归时先用一个变量取得myPow(x,n/2)的值再平方，可以降低时间复杂度（减少递归调用的次数）

double myPow(double x, int n){
    double t=1;
    if(n==0)return 1;
    else if(n==1)return x;
    else if(n==-1)return 1/x;
    else
    {
        if(n%2==0)
        {
            t=myPow(x,n/2)*myPow(x,n/2);
        }
        else
        {
           t=x*myPow(x,(n-1)/2)*myPow(x,(n-1)/2);
        }
        
    }
    return t;
}

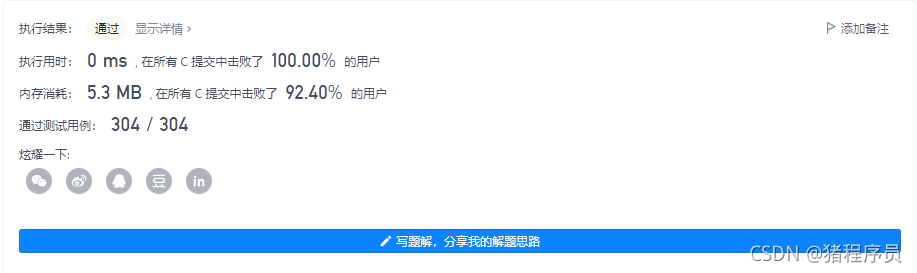
方法三:二分思想（执行用时：0 ms 内存消耗：5.3 MB）

通过二分的思想，我们可以通过x = x^2的操作将幂指数n降低至n/2，直到n=0为止。这样相比于一次一次乘效率提高了不少，因为使用单次累乘每进行一次幂指数n降低至n-1，而二分累乘幂指数n降低至n/2。
既然是对幂指数n除2操作，那不得不考虑这个n是奇数还是偶数，如果n为偶数，x^n =x^ (2)n/2；如果n为奇数xn =x*x^ (2)(n-1)/2

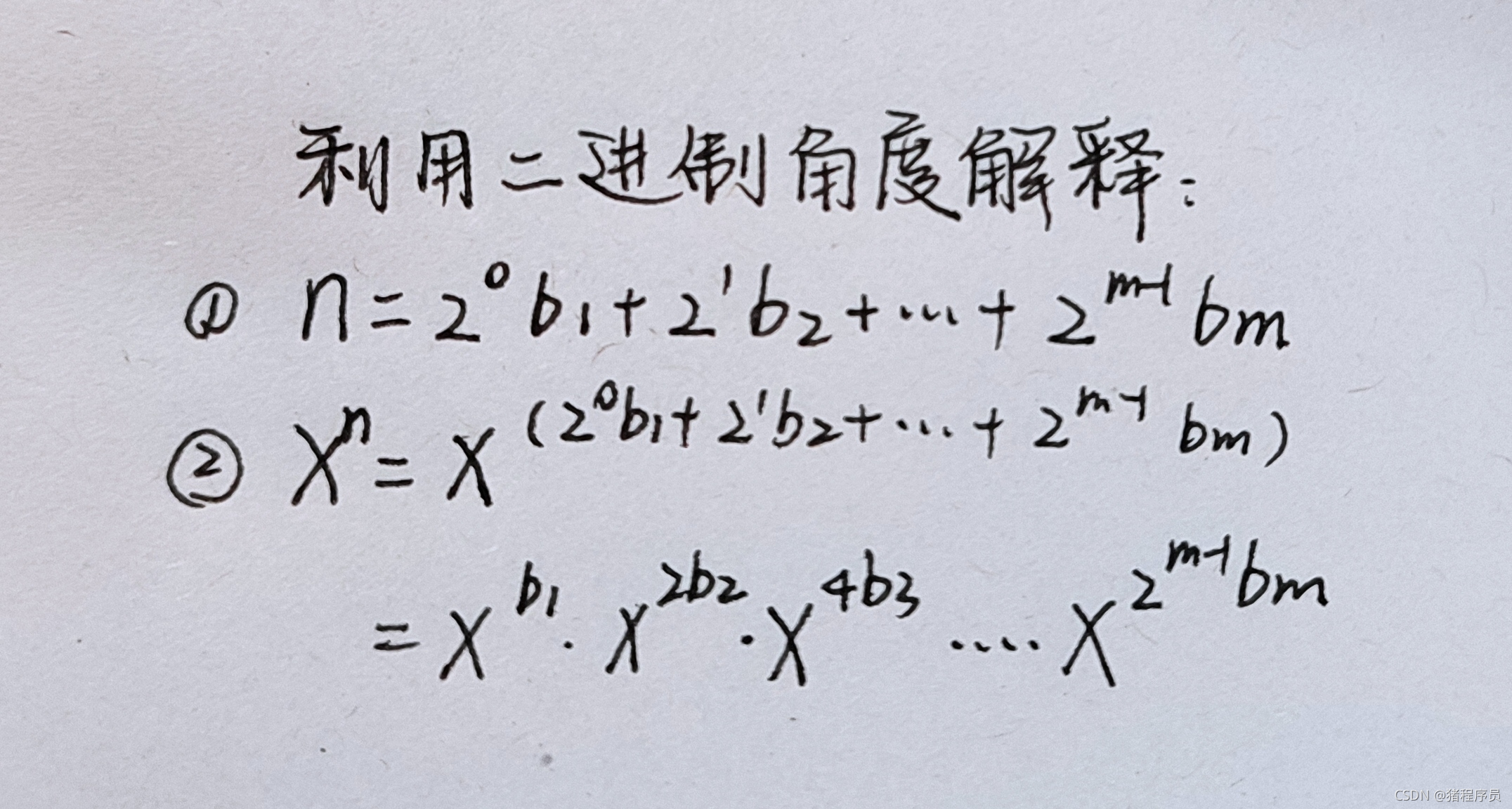
double myPow(double x, int n){
    int i = 0;
    double ret = 1.0;
    long m = n;//如果n为最小负数，对n取绝对值后会溢出，所以需要long型变量来储存
    if (x == 1 || n == 0)
        return 1.0;
    if (x == 0)
        return 0;
    if (n < 0)
    {
        m = -m;
        x = 1 / x;
    }
    while (m)
    {
        if (m & 1)
        {
            ret *= x;//如果n为奇数，对结果补乘一个x；如2的5次方可以转换成4的2次方再乘2
        }
        m >>=  1;
        x *= x;
    }
    return ret;
}

对于上述while循环的代码我初看的时候其实没有看懂，但我自己举了一个例子之后发现就清晰很多了，如果大家不明白的话也可以自己动手举例子！