原创开源思路下载链接,允许转卖
链接:https://pan.baidu.com/s/13aSy2-hlkLa7Ps8wknYY1Q
提取码:gap4
这里有百种算法出处整理,本题算法可从上面找取:
给裸赛的家人们整理了百种算法出处https://mp.weixin.qq.com/s/OhWRCeep885MuyhMhvdiOw
附件1画的图,为每块反射面链接主锁节点的位置
X=xlsread('附件1.csv');
figure
plot3(X(:,1),X(:,2),X(:,3),'*')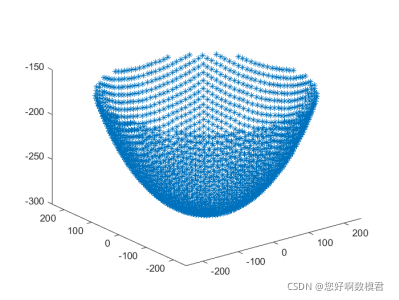
附件2画的图,每个主锁有上下两端点,为什么要给呢,一是主锁倾斜方向就是促动器的作用力方向,就算是之后的工作状态主锁的倾斜方向也不会有太大变化,可忽略;二是结合附件1可以得到每块反射面基准态时的倾斜方向角度,因为每块反射面的角点与其对应的主锁上端点的距离是固定的,需要先计算出来
X=xlsread('附件2.csv');
figure
plot3(X(:,1),X(:,2),X(:,3),'b*')
hold on
plot3(X(:,4),X(:,5),X(:,6),'r*')有些同学会发现,附件1和附件2的上端点对不上,确实是的,但是每个上端点与反射面角点的间距是固定的,所以后面改变下拉索伸缩时,反射面角点的位置有了与主锁上端点距离,以及主锁方向上的拉伸可以重新计算出反射面角点的位置
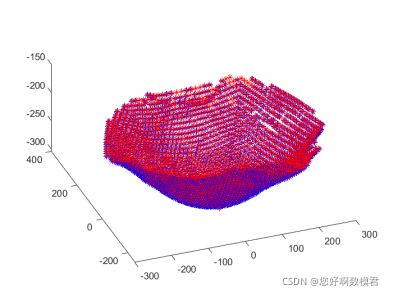
附件3结合附件1画的图
[~,~,X1]=xlsread('附件1.csv');
[~,~,X2]=xlsread('附件3.csv');
X1=string(X1);X2=string(X2);
X1(1,:)=[];X2(1,:)=[];
figure
hold on
a=[];b=[];c=[];
for i=1:size(X2,1)
a=find(X1(:,1)==X2(i,1));
b=find(X1(:,1)==X2(i,2));
c=find(X1(:,1)==X2(i,3));
plot3(double(X1([a,b,c],2)),double(X1([a,b,c],3)),double(X1([a,b,c],4)),'b-*')
end
中国天眼图,这道题可以不用考虑每个主锁节点和反射面的重量,题目也没给,实际中就算是有重量,基准态时促进器也会给予一定作用力来保持球面形貌,在这道题中我们就假设基准球面是一个球形面,并且工作态时的照射面会形成一个椭球形面

题目中的α和β为方位角和仰角,注意α是x与y轴的夹角,β是CS线与xy平面的夹角
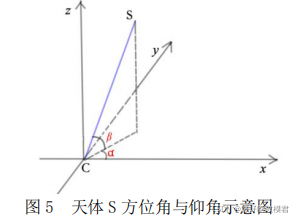
来看下附录:第7点需要理解下
基准状态下,促动器顶端径向伸缩量为0,其径向伸缩范围为-0.6~+0.6 米,这个条件就是刚刚说到的基准态时促进器也会给予一定作用力来保持圆球形貌,所以会有一个伸缩控制范围,但是需要注意调整工作抛物面需要促动器联动,那么如何分析呢,其实SC直线与基础球形面的垂线的交点就是照射面的中心,那么我们可以认为该中心的下拉索收缩幅度是最大的,而照射面边界点的下拉索会有一定伸长,其伸长是所有主索最大的,其实我们结合实际想想,最后会形成一个照射面截面为圆的椭球体面,那么空间的椭球体公式为(x-x1)²/a²+(y-y1)²/b²+(z-z1)²/c²=1,其中(x1,y1,z1)为椭球体的中心点,我们可以取一些参考点来推算该公式,为了多将光线反射至馈源舱,肯定照射面中心会有合理的凹陷,那么对于边界点的下拉索也有合理的伸长
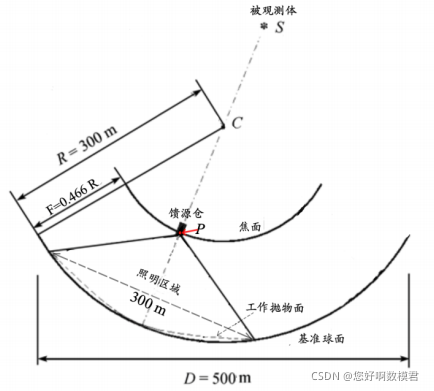
下面理想抛物线
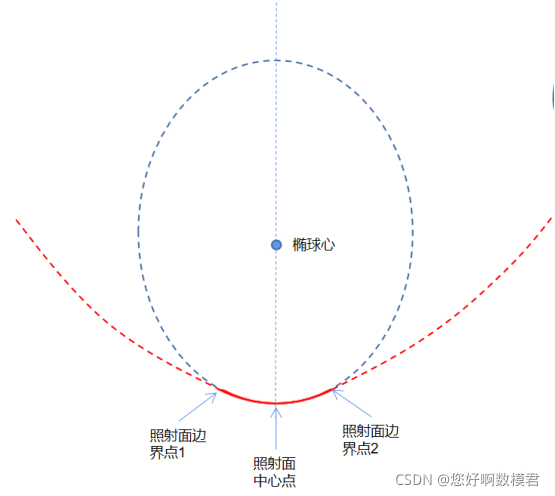
上面还不理解就看下图,其实理想抛物面就是椭球体一部分,照射区应当为椭球体形貌,那么本文为了好做分析,可以直接用椭球体方程,只求照射面没什么影响,照射面就是下图红色实线部分。接下来我们找一下参考点去推算公式,第一个照射面中心点就是SC垂线与基础球面的的交点,然后计算工作时下拉索收缩后该点的位置,然而具体收缩多少是我们后面要寻优的;然后找出基础球形面上到达SC直线近似150m距离的点,作为照射区的边界点,对于该类参考点,计算工作时下拉索伸长后该点的位置,同样的对于伸长多少,这里也是需要寻优的,不管怎么样即使第二类参考点也要收缩,那也要比第一个参考点收缩更小一点;有了这两类点,我们还缺椭球体公式中的中心点(x1,y1,z1),但是大家想想我们知道了边界点和中心点,但是未知其他位置的工作时的形貌,只知道是一个理想的抛物面,也就是的椭球体面,然而椭球体的中心点位置是会影响到其余照射区的形貌的,但是我们能知道椭球体的中心点在SC直线上,这里我们可以对椭球体中心点到照射中心点的距离进行寻优,从而推出椭球体公式;以上三类点足够推出该椭球体公式了,至于照射区域,参考题目给的图4,就考虑最大照射区就行,然后寻优得到他的形貌公式,有了该椭球体公式,椭球主轴又与SC直线重合,接下来分别求基础圆面和椭球体与SC的交点,然后以基础圆面上各节点与SC直线的交点做弧长距离,按该距离取对应椭球体面上找到相应的位置,通过计算照射区内前后位置变化就可以求得各节点对应的主索伸缩情况

这道题本是一个优化问题,可以观察这幅图可以看一下工作区的形貌变化
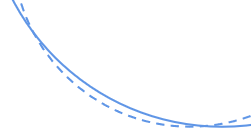
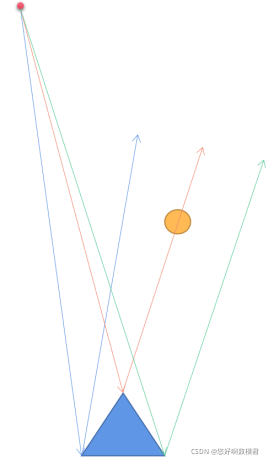
第一问自变量有照射中心的主索伸缩量、照射区边界点主索伸缩量(照射区边界点主索伸缩量应当相同)、椭球体中心到照射中心的距离(先有照射中心主索伸缩量在生成该参数),以上参数会得到一个椭球体面,基础圆面和椭球体面与SC直线会得到两个交点,根据弧长距离对应取得照射区主索的更新位置,然后计算主索的伸缩量,要找到最优的抛物面,肯定是要求更多的反射片能够反射至馈源舱内,馈源舱为直径为1m的圆,反射片为三角形,如下图,只要反射的光线能涵盖馈源舱部分都可以算是反射成功,目标函数可以定位能够将目标反射至馈源舱的反射片数,第三问在考虑反射的面积,这里还要计算出各三角形反射片的角点,以确定其倾斜方向,然后去算反射线能达到馈源舱,对于光线反射问题,反射片的垂线作为主轴去算就行,可能程序有点繁琐
第一问就考虑正上方的天体,第二问考虑其他位置的,大家也不用去纠结前面讲的照射区,按α=36.795°,β=78.169°方向,注意方向是以基础圆面中心垂直线来参考的角度的,按SC线算的的照射区口径差不多就是300m了,第二问没有给天体高度距离来算,或者如果想讨论不同天体高度距离也可以,天体所处位置方向不变就行。第二问同样按照第一问模型来做寻优
第三问则是要考虑上每块反射片,反射光线后能照射到馈源舱圆形上的面积之和,目标函数改为这个其他步骤同理,最后就基础球面对比