一、本章重点
★ 微处理器、微型计算机和微型计算机系统的区别;
★ CPU的主要功能和组成部件;
★ 微型计算机的性能指标;
★ 二进制补码运算。
二、引入部分
学习这一章内容,首先我们还是需要知道几个重要的概念:
① CPU,微处理器,它是计算机的核心,其包括运算器、控制器、寄存器组;
② 存储器,用于存放计算机工作过程中需要操作的数据和程序;
③ 内存单元的地址和内容,内存按单元组织,每单元都对应一个地址,以方便对单元的寻址。

④ 内存容量:所含存储单元的个数,以字节为单位,内存容量的大小依CPU的寻址能力而定,实地址模式下为CPU地址信号线的位数。
⑤ 内存操作,读:将内存单元的内容取入CPU,原单元内容不改变;写:CPU将信息放入内存单元,单元中原来的内容被覆盖。
三、知识点
1、微处理器、微型计算机和微型计算机系统的关系如图一所示。
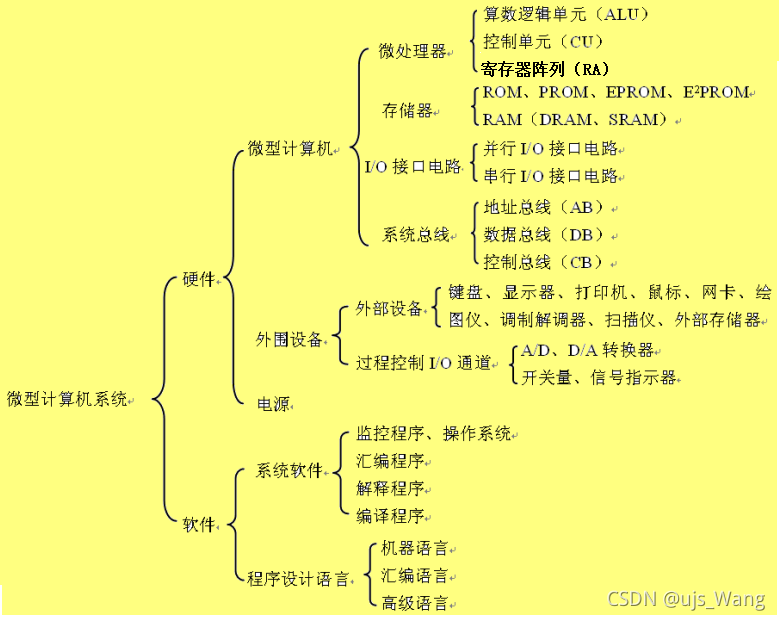
图一 微机系统的组成
2、微处理器CPU
(1)内部结构由算术逻辑部件、累加器和通用寄存器组、控制器组成。其中控制器又包含:指令寄存器:存储指令;译码器:对指令进行译码、分析,并产生控制信号;时序和控制电路:提供整个系统所需要的定时和控制;中断机构:处理异常、响应其他部件发来的中断请求。
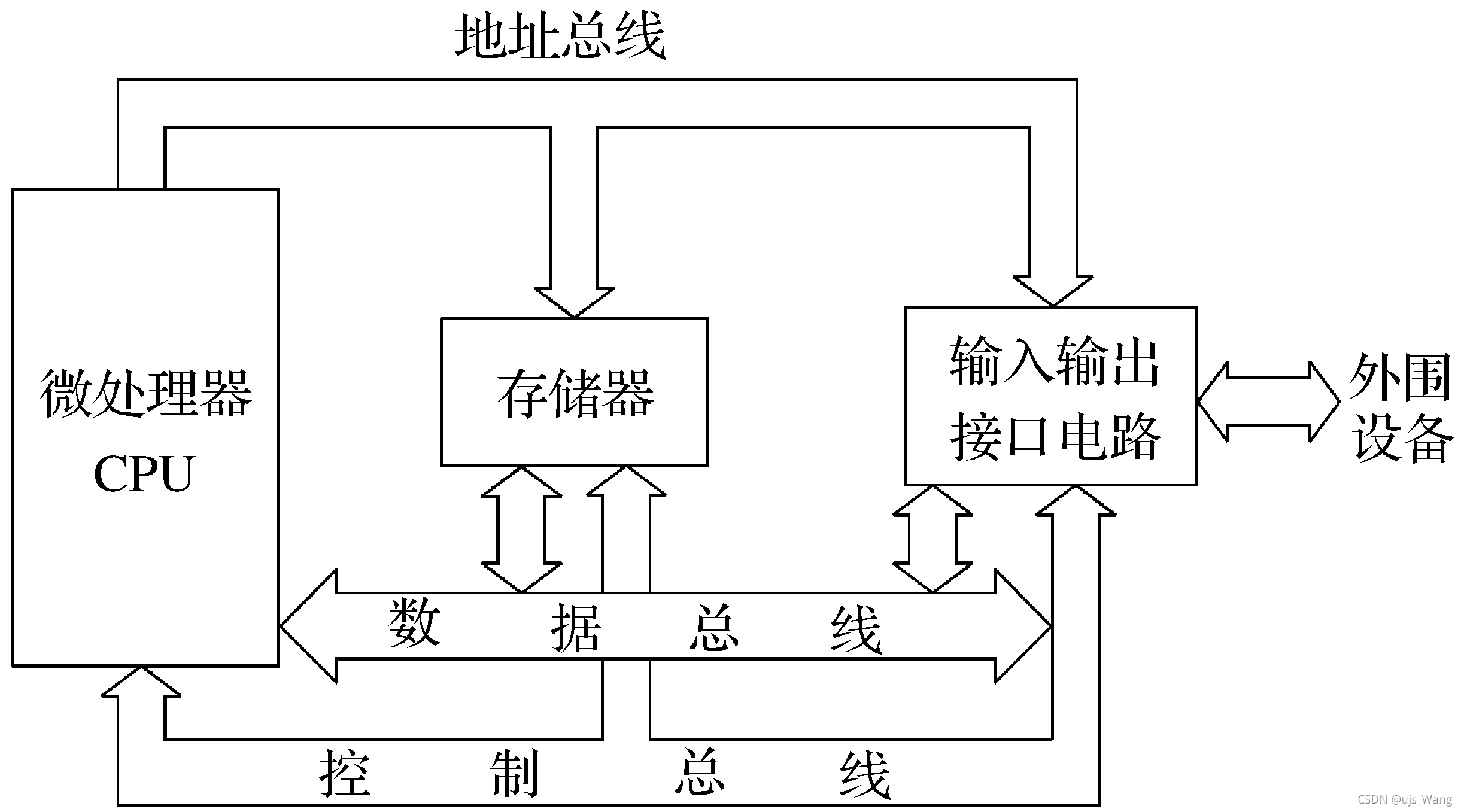
图二 微型计算机的基本结构以及CPU在此的作用
其中,CPU总线是CPU和其他部件之间进行信息传输的通道。
(2)CPU总线分类
- 数据总线DB(data bus):用来传输数据,是双向的。数据总线的位数(宽度)是微型计算机的一个重要指标,和微处理器的位数相对应。
- 地址总线AB(address bus):用来传送地址信息,是单向的。地址总线的位数决定了CPU可直接寻址的内存范围。8086CPU有16根数据线和20根地址线,所以可寻址的地址空间最大为220B=1MB。
- 控制总线CB(control bus):传输控制信号。CPU送往存储器和输入输出接口电路的控制信号。(读、写、中断响应信号等);其它部件送往CPU的信号。(时钟信号、中断请求信号等)。
(3)CPU基本功能
① 可进行算数和逻辑运算;
② 可保存较少量数据;
③ 能对指令进行译码并执行规定的动作;
④ 能与存储器、外设交换数据;
⑤ 提供整个系统所需要的定时和控制;
⑥ 可以响应其他部件发来的中断请求。
3、微型计算机的性能指标
- 总线类型与总线速度;
- 主板与芯片类型;
- 外设的配置;
- 系统软件的配置;
- 可靠性、可用性和可维护性。
4、数制与编码
众所周知,计算机能识别的都是二进制数,因此下面进制的学习主要是二进制,若涉及到其他进制的,则是进制的转换了,无需深入。
(1)进制之间的转化
这部分学习数电的时候已经知道了,就不进行展开,如果还不清楚,可以参考微机原理的书或者数电的书。
(2)二进制数的运算方法
二进制的算数运算有加,减,乘,除,前三者我们都应该很熟悉,除法运算就拿上课举的第一个例子做思考,如图三所示。

图三 二进制数除法运算
(3)二进制数的逻辑运算
其实很简单,“0”则为“否”,“1”则为“是”,与运算中有0则运算结果就是0,都是1运算结果才是1;或运算中有1则运算结果就是1,都是0运算结果才是0;非运算中,1变0,0变1;异或运算中,相异出1,相同出0。
(4)无符号数和有符号数
所谓无符号数,通常表示一个数的绝对值,即数的各位都用来表示数值的大小;有符号数就是要看最高位,如果最高位是1,就是负数,最高位是0,就是正数,例如+18就是二进制数00010010,-18就是二进制数10010010.
(5)原码,反码,补码
①原码。在(4)中,以最高位为0表示正数,1表示负数,后面各位为其数值,这种数的表示方法为原码表示法。例如,令X=00010010B,Y=10010010B,则[X]原=00010010B,[Y]原=10010010B。
补充:0有+0和-0之分,+0就是00000000B,-0就是10000000B。
②反码。正数的反码和其原码相同,例如在①中,[X]反=[X]原=00010010B;而对于负数,则将其原码除符号位以外各位按位取反,例如在①中[Y]反=11101101B。
③补码。正数的补码和其原码相同,例如在①中,[X]补=[X]原=00010010B,最高位是符号位,其余为数值位;负数的补码就是其反码加1,也就是它的原码初符号位外其余数值各取反再加1,例如在①中[Y]补=11101110B。
(6)补码的运算
两个用补码表示的有符号数进行加、减运算时,其特点是把符号位上表示正、负的“0”和“1”也看成数,与数值部分一同进行运算,所得的结果也为补码形式。
结果的符号位为“0”,表示正数;结果的符号位为“1”,表示负数。例如:
① 两个有符号数X和Y进行相加时,先将两个数分别转换为补码的形式,然后进行补码加运算,所得的结果为和的补码形式,即:[X+Y]补=[X]补+[Y]补。
如图四所示即为补码的加法运算。
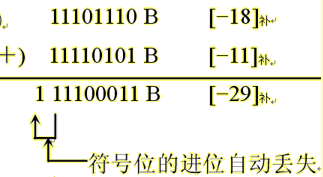
图四 补码的相加
② 两个有符号数相减,可通过下面的公式进行:
[X-Y]补=[X]补+[-Y]补,如果已知[Y]补,那么对[Y]补的每位(包括符号位)都按位求反,然后末位加1,结果即为[-Y]补,一般,称[−Y]补为对[Y]补的“变补”,即[[Y]补]=[-Y]补,已知[Y]补求的[−Y]补过程称为变补。
这样,求两个带符号的二进制数之差,可以用“减数(补码)变补与被减数(补码)相加”来实现。这是补码表示法的主要优点之一。我们在这里也举一个上课PPT的例子,如图五所示,求解96-19的过程。

图五 二进制补码的减法运算
(7)溢出
在学习这个概念之前,先举个“13+7=?”例子,如图六所示。
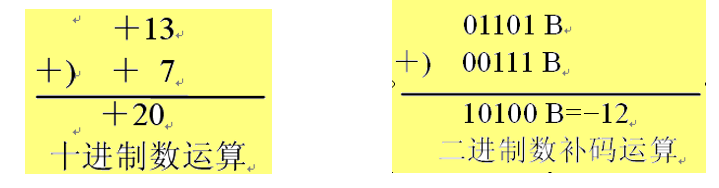
图六 溢出的典例
我们发现在这个例子当中,13+7=-12,这显然是不可能的,产生错误的原因是由于两个数相加后的数值超出了加法装置所允许位数(数值部分4位),因而从数值的最高位向符号位产生了进位,或者说这种现象是由于“溢出”而造成的。
那我们如何判断是否产生溢出呢?这里介绍双高位法帮助我们来判断。双高位法就是如果符号位和数值部分的最高位产生进位情况的异或结果是1,则产生溢出,是0则没有产生溢出现象。我们举两个例子如图七和图八所示。
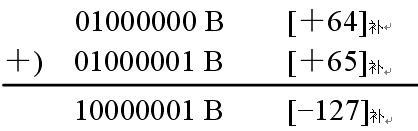
图七 产生溢出情况
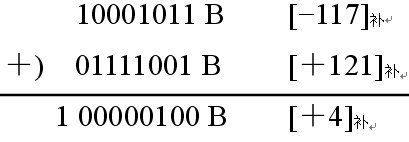
图八 不产生溢出情况
在图七中,数值部分的最高位(两个1)相加产生了进位,而符号位(最前面的00)没有产生进位,所以它们异或的结果是1,即产生了溢出。
在图八中,数值部分最高位由于前面进位了一个1,所以相加产生了进位,进到符号位再相加,符号位也产生了进位,因此它们异或的结果是0,没有产生溢出。
四、参考文献
[1] 程启明等.微机原理及应用[M].北京:中国电力出版社,2016.
[2].清华大学微机原理与接口技术课件.
[3].江苏大学微机原理与接口技术课件.