目录
- 🔞0.前言:
- 🔞1.常见进制介绍:
- 🎈(1)十进制:
- ①示例:
- ②可知一个任意多位的十进制数D均可展开为如下形式:
- ③拓展—— 若以N取代式中的10,即可得到多位任意进制(N进制)数展开式的普遍形式:
- 🎈(2)二进制:
- ①根据N进制数展开的普遍形式可得任意一个二进制数均可展开为: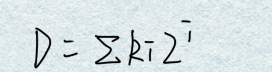
- ②并可利用上式计算出任一二进制数所表达的十进制数的大小:
- 🎈(3)八进制:
- ①根据N进制数展开的普遍形式可得任意一个八进制数均可展开为:
- ②并可利用上式计算出任一八进制数所表达的十进制数的大小:
- 🎈(4)十六进制:
- ①根据N进制数展开的普遍形式可得任意一个十六进制数均可展开为:
- ②并可利用上式计算出任一十六进制数所表达的十进制数的大小:
- 🎈(5)不同进制数的对照表:
- 小拓展:
- 🔞2.不同进制间的转换:
- 🎈(1)八进制,二进制,十六进制转换为十进制:
- 🎈(2)十进制转换为二进制,八进制,十六进制:
- ①十进制转换为二进制:
- ②十进制转换为十六进制:
- ③十进制转换为八进制:
- 🎈(3)二进制转换为十六进制:
- 注意:
- 🎈(4)二进制转换为八进制:
- 注意:
- 🎈(5)十六进制转换为二进制:
- 🎈(6)八进制转换为二进制:
- 🎈(7)八进制与十六进制之间的转换:
- 3.In The End!
🔞0.前言:
- 👻👻某些大牛曾说过:一个优秀的程序猿, 他不仅软件层面玩的好;而且硬件层面也玩的花。 👻👻
「华为天才少年」——稚晖君的光辉事迹想必大家有有所耳闻:
就比如前一段时间网上爆火他的一件神仙之作——耗时仅四个月,开发出的一款完美的自动驾驶自行车!
需要注意的是:这个作品从构思到实物产出(CAD车体建模,载板PCB设计,手工焊接,总线控制,RPC通信,电机控制,传感器数据,ROS信息分发,SLAM建图,图像分类,PID,卡尔曼滤波数据融合,参数整定…)全都经他一人之手。这是货真价实的全栈工程师,一个人堪比一整个技术团队!!!
- 😬😬而且当年他去面试OPPO的时候拿到了两份Super Special的offer:一个是硬件岗、一个是算法岗。 可能有的小伙伴要说——“这是天才,我们常人无法企及!”😬😬
普通人经过不懈努力——最后变得不普通的例子也不计其数!
比如最鲜为人知的例子:前乒乓球奥运冠军邓亚萍,从小个子长得慢,胳膊短,为了能提高乒乓球技能加倍苦练,成为乒乓球大满贯得主。
- 😜😜“确实,不得不承认人与人之间是有差距的”,但是我想说的是:“我们可能做不到他做的那么好,但是最基本的硬件知识/数电知识我们还是要了解的。”——正所谓:知其然,更要知其所以然!😜😜
知道的越少,不知道的就越少;知道的越多,不知道的就越多!
- 🐌🐌我会尽量把技术文写的通俗易懂/生动有趣,保证每一个想要学习知识&&认认真真读完本文的读者们能够有所获,有所得。当然,如果你读完感觉本文写的还可以,真正学习到了东西,希望给我个「 赞 」 和 「 收藏 」,这个对我很重要,谢谢了!🐌🐌
| 分栏名称 | 传送门 |
|---|---|
| 🎐爬虫难,跟我一起入爬虫坑,爬虫一条龙服务!🎐 | 《入坑Python爬虫》 |
| 🐲Django框架难,跟我一起一条龙教学(附带多个小型项目实战!)🐲 | 《Django框架一条龙》 |
| 🐋Scrapy框架难,跟我一起一条龙教学(附带多个小型项目实战!)🐋 | 《Scrapy框架一条龙》 |
| 🐠Tornado框架难,跟我一起一条龙教学(附带一个完整项目!)🐠 | 《Tornado框架一条龙》 |
| 🐝爬虫——JS渗透;三大验证码(滑块,点触,图形);字体反爬;移动端!🐝 | 《爬虫高级一条龙》 |
🔞1.常见进制介绍:
🎈(1)十进制:
在十进制数中,每一位有0-9十个数码,所以计数的基数是10。超过9的数必须用多位数表示,其中低位和相邻高位之间的关系是:逢十进一,故称为十进制。
①示例:
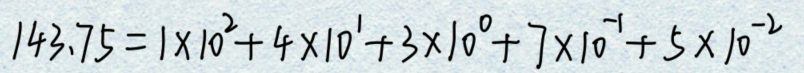
②可知一个任意多位的十进制数D均可展开为如下形式:
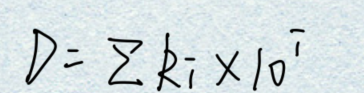
③拓展—— 若以N取代式中的10,即可得到多位任意进制(N进制)数展开式的普遍形式:
式中i的取值与十进制展开式的规定相同。
「变量详解」:
N称为计数的基数;
k为第i位的系数;
N称为第i位的权。
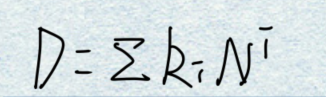
🎈(2)二进制:
目前在数字电路(我们生活在0和1组成的世界里!)中应用最广泛的是二进制。在二进制数中,每一位仅有0和1两个可能的数码,所以计数基数为2。其中低位和相邻高位之间的进位关系是:“逢二进一”, 故称为二进制。
①根据N进制数展开的普遍形式可得任意一个二进制数均可展开为: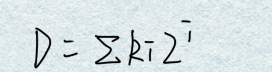
②并可利用上式计算出任一二进制数所表达的十进制数的大小:
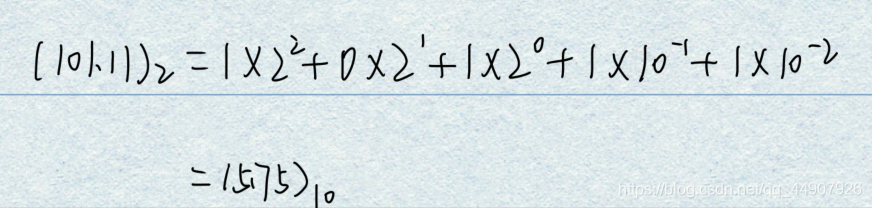
上式中分别使用下脚注2和10表示括号里的数是二进制数和十进制数。/有时也用B( Bima-ry)和D( Decimal)代替2和10这两个脚注。
🎈(3)八进制:
八进制数的每一位有0~7 八个不同的数码,在二进制数中,计数的基数为8。其中低位和相邻高位之间的进位关系是:“逢八进一”, 故称为八进制。
①根据N进制数展开的普遍形式可得任意一个八进制数均可展开为:
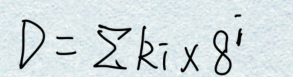
②并可利用上式计算出任一八进制数所表达的十进制数的大小:
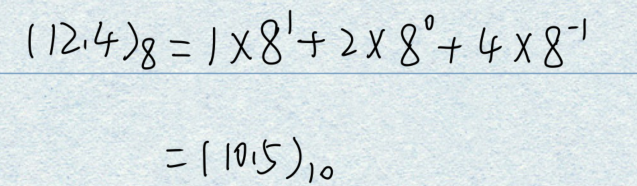
有时也用O(Oetal)代替下脚注8,表示八进制数。
🎈(4)十六进制:
十六进制数的每一位有十六个不同的数码,分别用0~9.A(10)、B(11) .C(12)、D(13)、E(14)、P(15)表示。在十六进制数中,计数的基数为16。其中低位和相邻高位之间的进位关系是:“逢十六进一”, 故称为十六进制。
①根据N进制数展开的普遍形式可得任意一个十六进制数均可展开为:
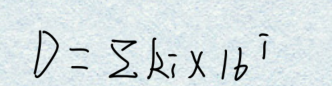
②并可利用上式计算出任一十六进制数所表达的十进制数的大小:
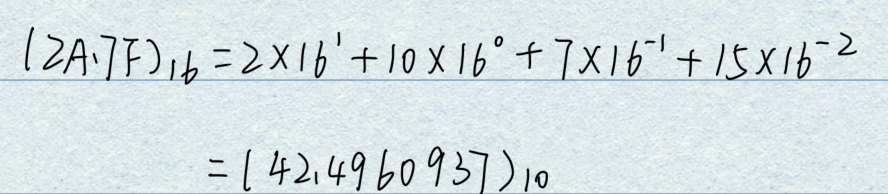
式中的下脚注16表示括号里的数是十六进制数,有时也用H( Hexadecimal)代替这个脚注,0X表示前缀。
🎈(5)不同进制数的对照表:
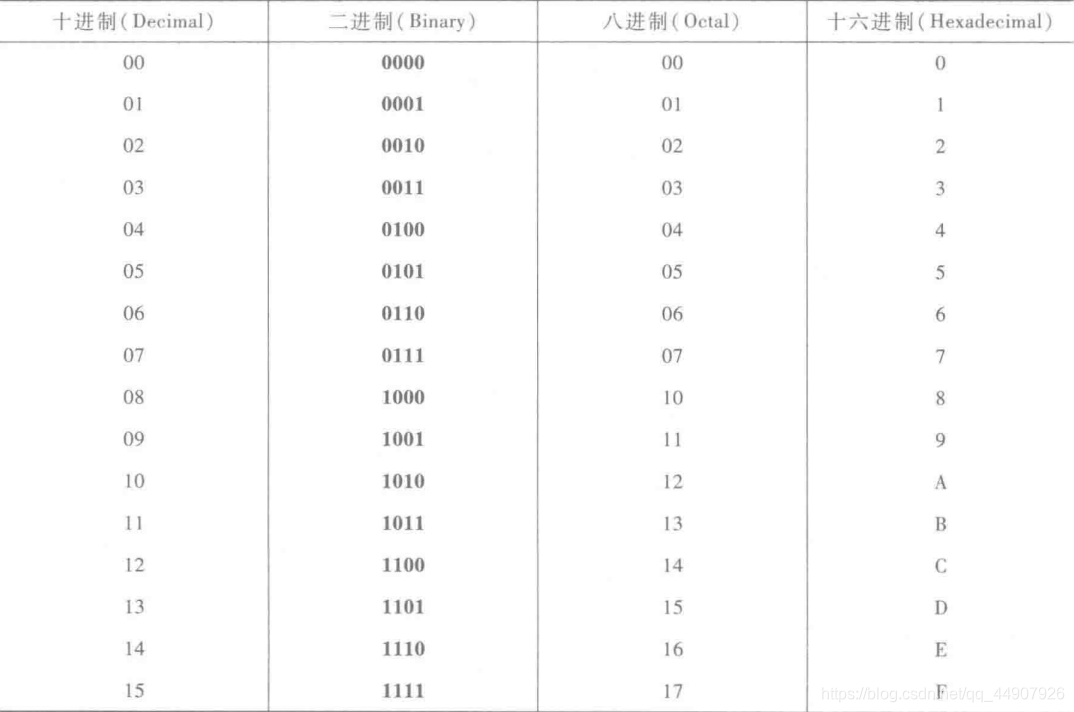
小拓展:
-
一位八进制可以表示三位二进制数:
解读:
因为三位二进制最小是000b,最大是111b,其范围恰好在0-7,构成了八进制一位。 -
一位十六进制可以表示为四位二进制:
解读:
十六进制数的进率是16,二进制数的进率是2,且16=2^4,说明二进制数连续进位4次,等效于16进制数进1位。这么说可能不好理解,那么举个例子吧,比如15+1=16,用二进制表示就是1111+1=10000,用十六进制表示就是F+1=10。这也就说明了一位十六进制数对应四位二进制数了
🔞2.不同进制间的转换:
🎈(1)八进制,二进制,十六进制转换为十进制:
都可根据上述介绍十进制的时候讲解的——多位任意进制数展开式的普遍形式进行转换,即按位权展开式。
🎈(2)十进制转换为二进制,八进制,十六进制:
十进制整数转换R进制(R可以是任何整数,比如2,8,16)整数,方法就是除R取余。
①十进制转换为二进制:
十进制整数转换为二进制方法:除二取余,从下往上倒序排序!

十进制小数转换为二进制方法:乘二取整,从上向下顺序排序!

②十进制转换为十六进制:
十进制数为整数时,除16取余;
十进制数为小数时,乘16取整。
(具体步骤拟同十进制转换为二进制!)
③十进制转换为八进制:
十进制为整数时,除八取余;
十进制为小数时,乘八取整。
(具体步骤拟同十进制转换为二进制!)
🎈(3)二进制转换为十六进制:
只要从低位到高位将整数部分每4位二进制数分为一组并代之以等值的十六进制数,同时从高位到低位将小数部分的每4位数分为一组并代之以等值的十六进制数,即可得到对应的十六进制数。

注意:
|
🎈(4)二进制转换为八进制:
只要将二进制数的整数部分从低位到高位每3位分为一组并代之以等值的八进制数,同时将小数部分从高位到低位每3位分为一组并代之以等值的八进制数,即可得到对应的八进制数。

注意:
| 二进制数最高一组不足3位或小数部分最低一组不足3位时,仍需以0补足三位! |
🎈(5)十六进制转换为二进制:
转换时只需将十六进制数的每一位用等值的4位二进制数代替即可!

🎈(6)八进制转换为二进制:
转换时只需将八进制数的每一位用等值的3位二进制数代替即可!

🎈(7)八进制与十六进制之间的转换:
第一种:先转成二进制然后再相互转换;
第二种:先转成十进制然后再相互转换!
| 建议:先将八进制转换为对应的二进制,再将二进制转换为十六进制! |
3.In The End!

| 从现在做起,坚持下去,一天进步一小点,不久的将来,你会感谢曾经努力的你! |
本博主会持续更新爬虫基础分栏及爬虫实战分栏,认真仔细看完本文的小伙伴们,可以点赞收藏并评论出你们的读后感。并可关注本博主,在今后的日子里阅读更多技术文!
如有错误或者言语不恰当的地方可在评论区指出,谢谢!
如转载此文请联系我征得本人同意,并标注出处及本博主名,谢谢!!