神奇的树
- 引言---树的故事
- 树的基本性质和描述
- 树的基本特点
- 树的关键字解析
- 树的表示方法
- 二叉树的概念结构
- 特殊二叉树
- 二叉树的性质
- 二叉树的存储结构
- 二叉树与堆
- 堆的实现
- 堆排序
- 堆的功能实现
- 堆的插入
- TOPK问题
- 二叉树的结构以及实现
- 二叉树的遍历
- 代码实现
- 程序实现方法 以及递归小技巧
引言—树的故事
在自然界中有很多树 它们是这样的

但是在我们的眼中 他是这样的

显而易见 树的特点就是一对多 ,我们利用这个一对多的特点,可以让我们更好的解决编程中的问题,在树中 ,最基础的二叉树是我们的重点研究对象。
在看一眼神奇的堆排序的动态图

做事情,先求对,在求巧,一步一步才可有所成就,所以让我们从基础开始吧!
树的基本性质和描述
树是一个一对多的特殊数据类型,树的根在上 叶子在上 。有种一生二,二生三,三生万物的感觉。
树的基本特点
-
树有且只有一个根,且根没有后继结点。
-
树是互不相交的
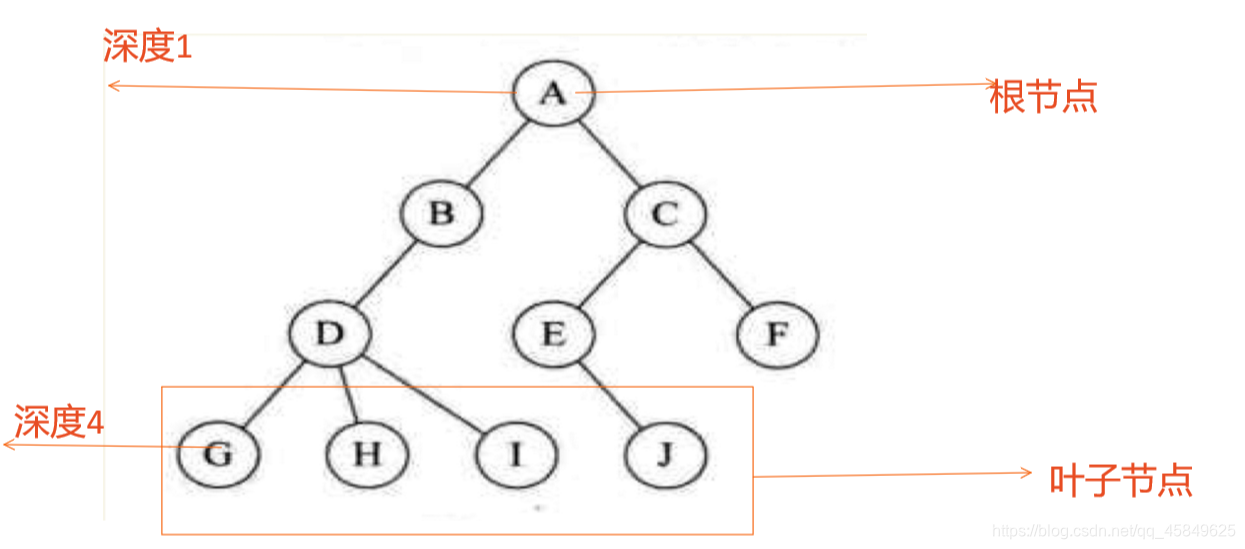
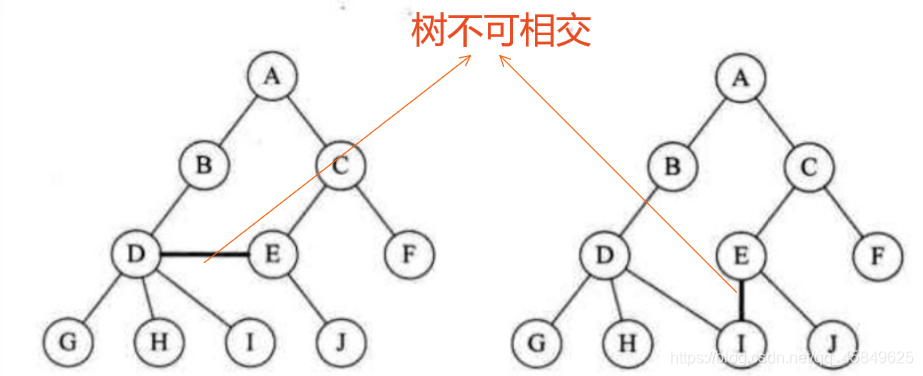
ps: 图可知 不构成闭合回路则不相交。 -
每一个结点可在分为一个子树。
-
树的定义是一个递归定义,即树在定义时又会用到树的概念,他道出了树的固有特性。
树的关键字解析
树有一大段关键字很让人头疼
结点的分类:
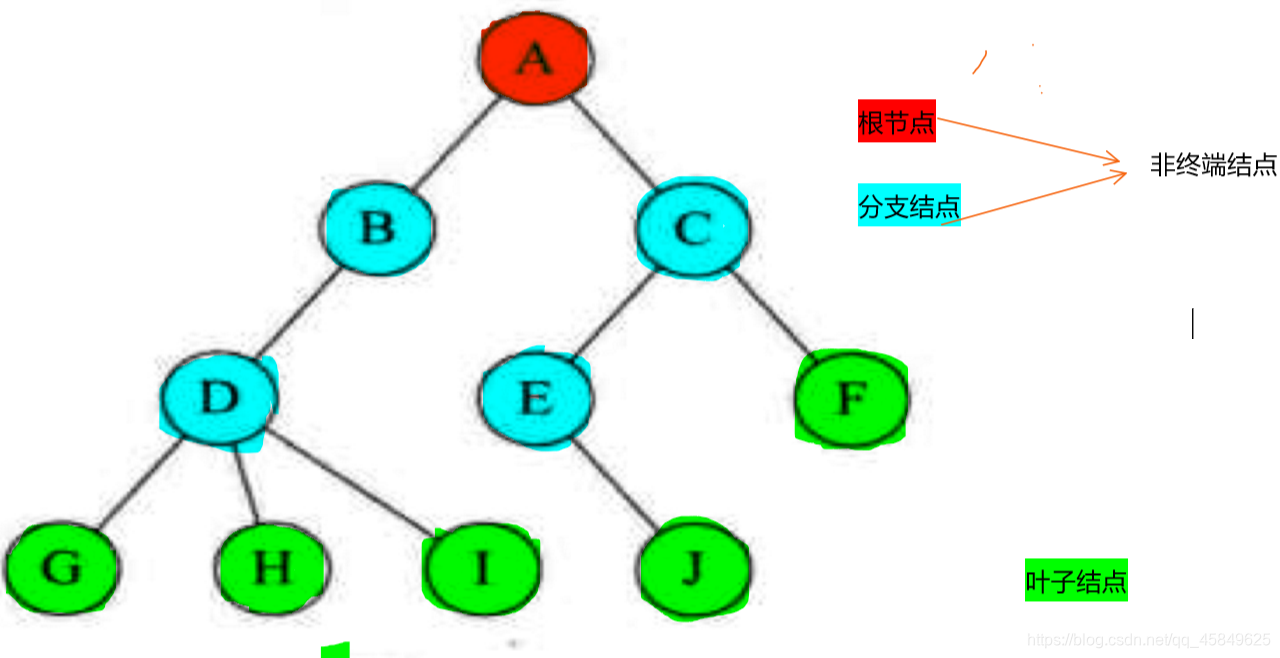
ps:
- 结点的度: 结点拥有的子树数称为结点的度。度为0的点成为叶节点或终端结点,度不为0的节点称为非终端结点。树的度是树内各个结点的最大值。此图 D为最大的结点,
- 结点的层次:从根开始为第一层,依次递增
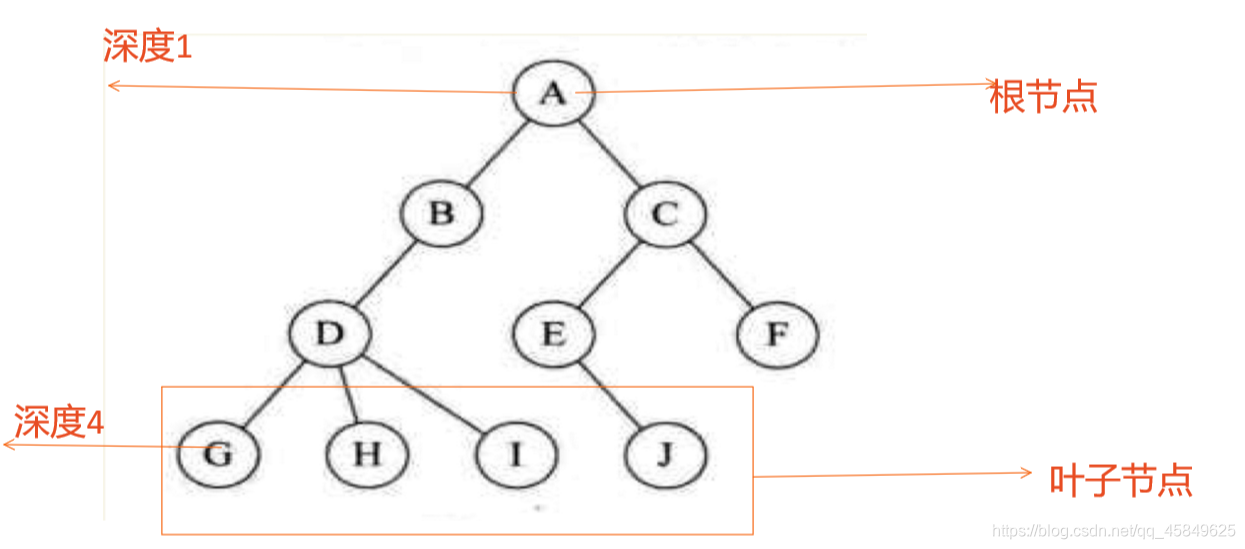
简单对比 树形结构与线性结构:
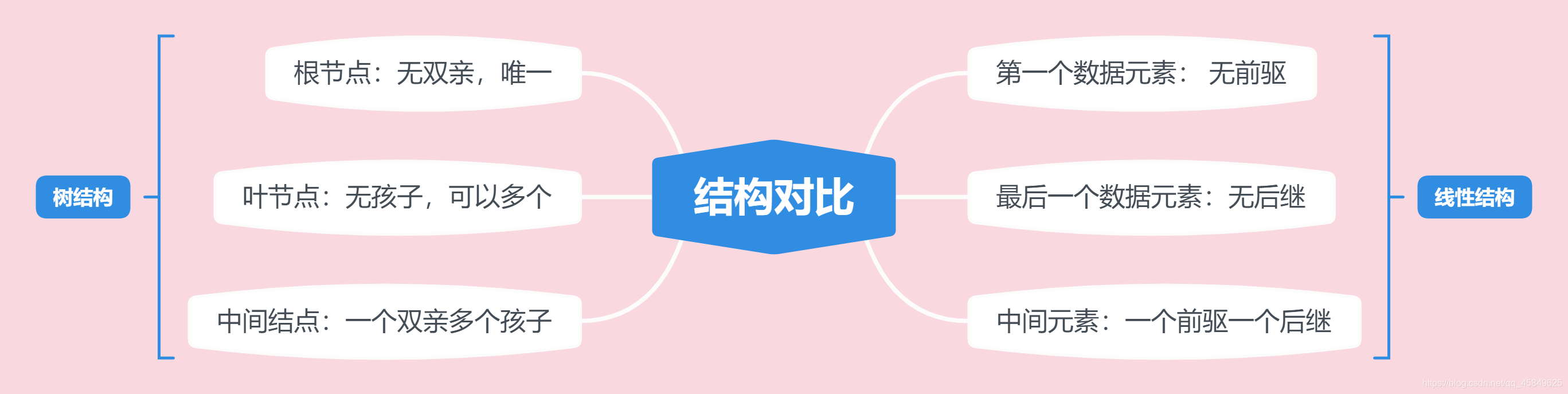
树的表示方法
- 双亲表示法
typedef struct
{
int data;
int parent; // 双亲位置
}PtNode;
typedef struct
{
PtNode nodes[10];
int root ;
int n;
}PTree;
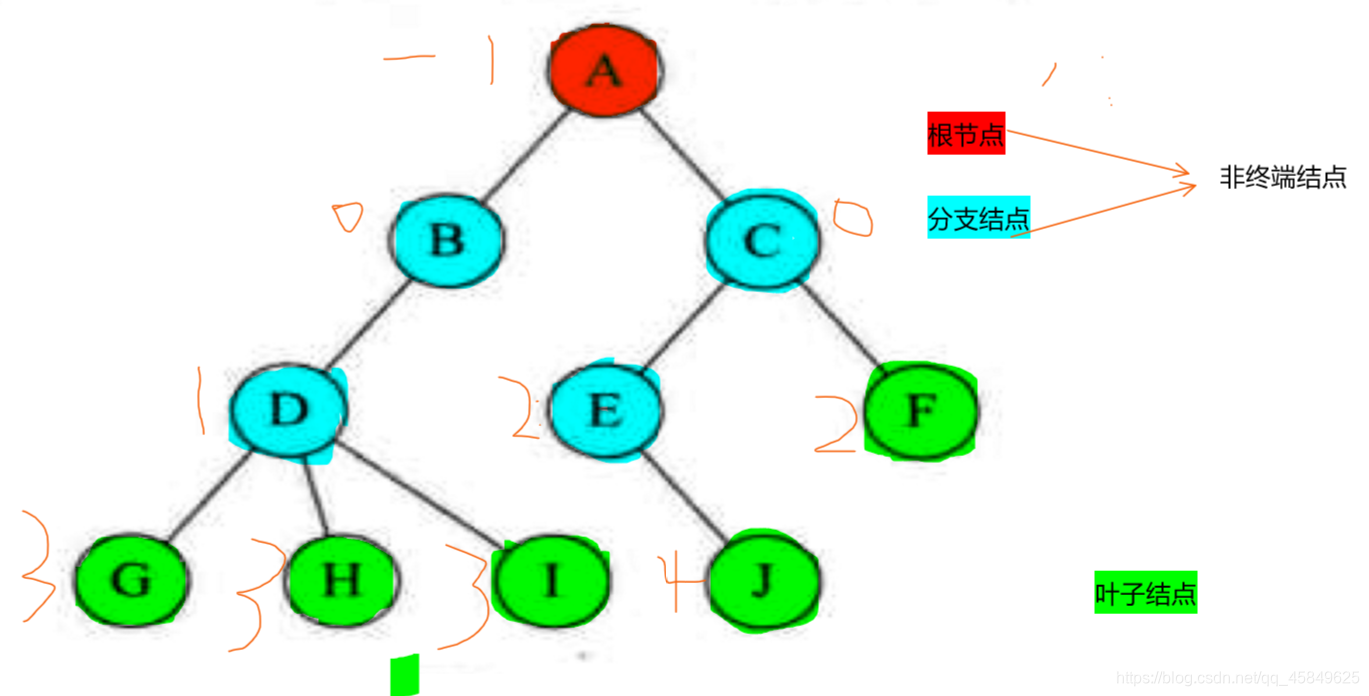
此图数字表示父亲的结点
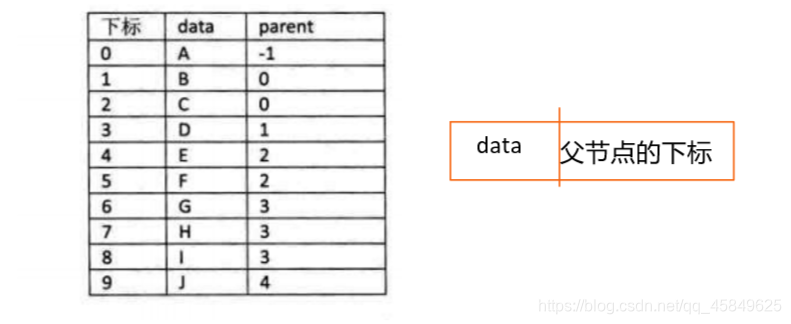
通过“父亲的下标”即可找到父亲的位置
注:
-
找双亲时间复杂度 O(1);找结点儿子需要遍历树
-
数据的增删查改。
-
左孩子右兄弟
typedef struct CSNode
{
int data;
struct CSNode* firstchild, * rightsib;
};
左孩子右兄弟的方式就是 多一个指针 一个指针指向自己最左侧的孩子 另一个指针指向自己右侧兄弟
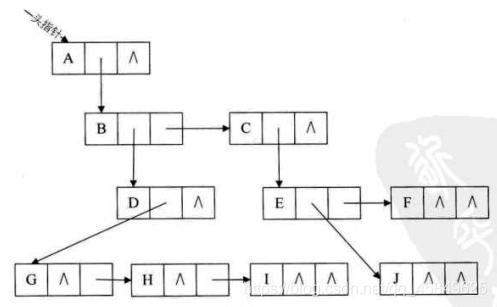
这种表示法是我们常用的表示法。
二叉树的概念结构
二叉树
二叉树是一种特殊的树,他的特点是一个根节点两个子节点,这两个子节点又分别叫做左子树和右子树。

注意
- 二叉树的度不超过二
- 二叉树左右子树不可颠倒
- 二叉树有且只有一个子树时,也需要区分左右。
特殊二叉树
满二叉树
一个二叉树每一层都是满的,那么这个二叉树就是满二叉树。如果一个二叉树的层数为k,且结点总数是(2^k)-1
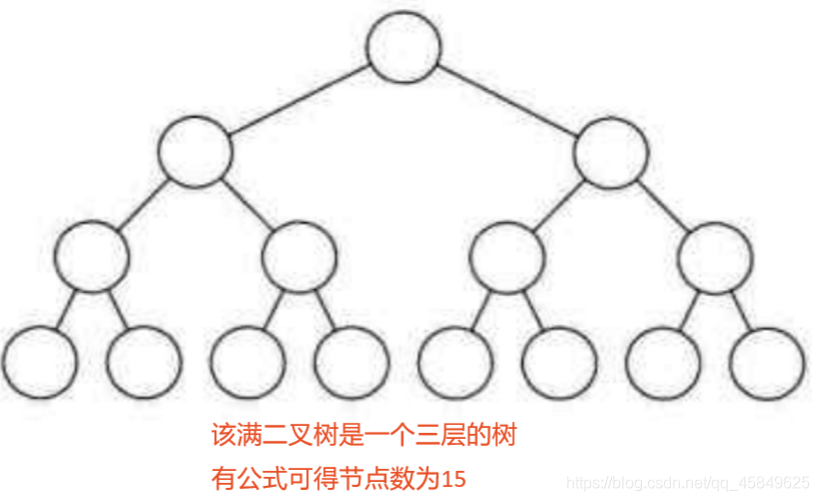
完全二叉树
一个完全二叉树的前k层都是满的第k层可以不满 ,但是必须连续,及满足先左后右。
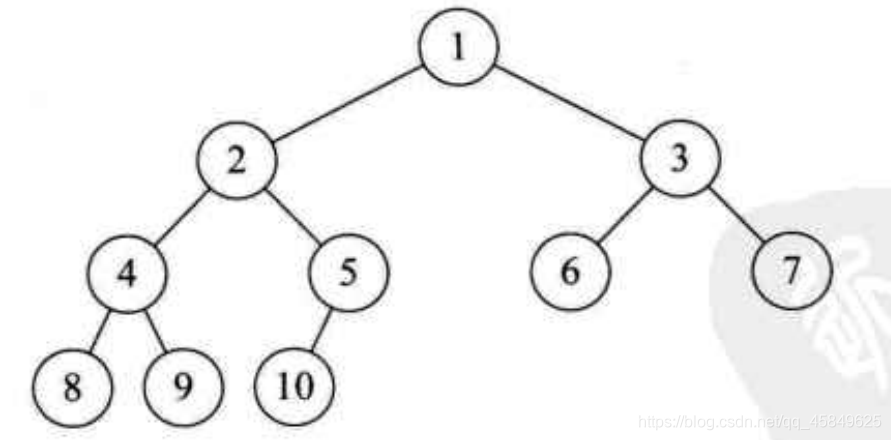
注意
- 满二叉树一定是完全二叉树,反之就不对。
- 完全二叉树一定是先左后右,如下图则不对
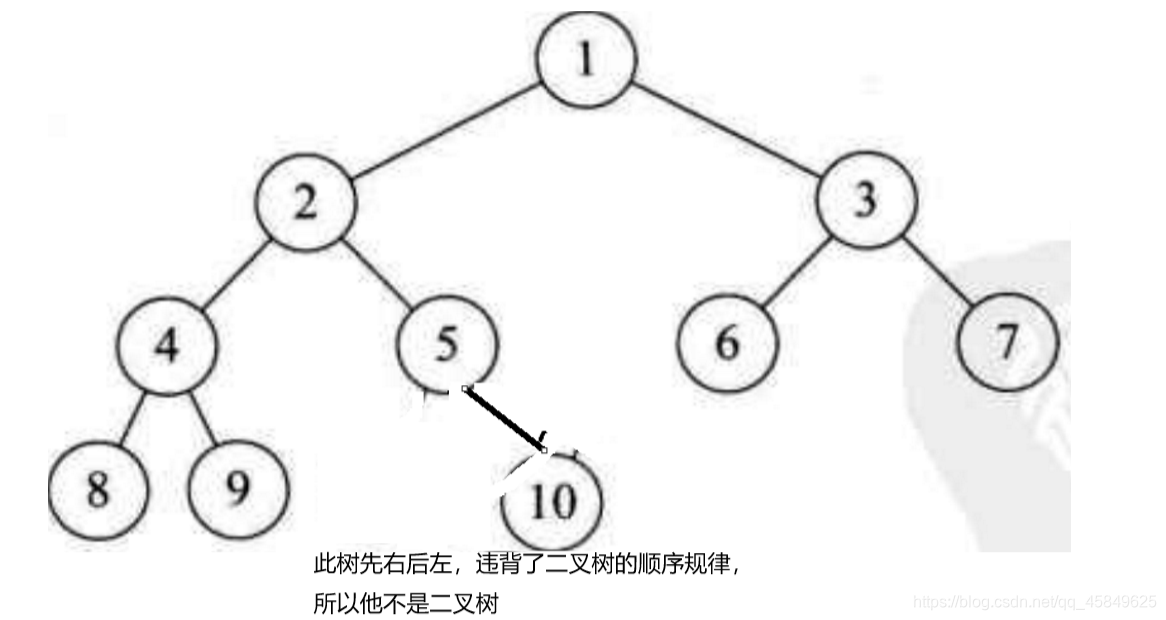
- 完全二叉树叶子的结点都在最后两层,左侧集中最后第k层的叶子,右侧集中第k-1层的叶子
二叉树的性质
-
在二叉树的第i层上至多有2^(i-1)的结点i>0
-
深度为k的二叉树至多有2^k-1个结点
-
对任何一个二叉树T,如果其终端结点树为n0,度为2的结点树为n2则no=n2+1;
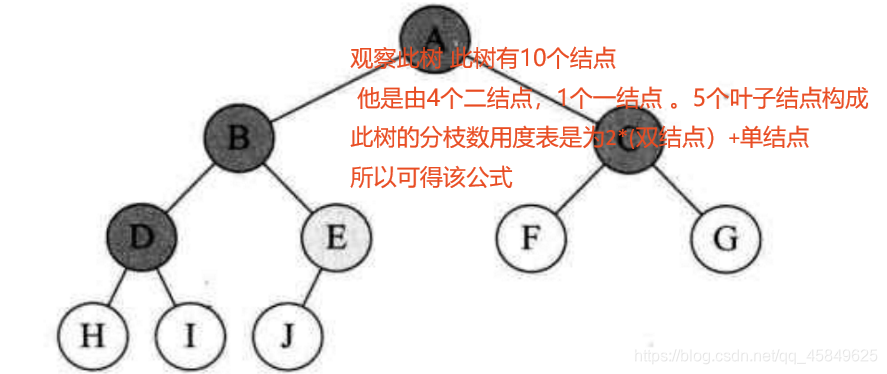
-
具有n个结点的完全二叉树的深度为log2(n)+1
-
对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序从0开始编号,则对与序号为i的结点有:
1. 若i>0,i位置结点的双亲序号为(i-1)/2;
2. 若2i+1<n,左孩子序号:2i+1,2i+1>=n则无左孩子
3. 若2i+2<n,右孩子序号;2i+2,2i+2>=n则无有孩子假设父亲的结点序号为parent,左孩子为leftchild,右孩子为ringhtchild。 有: leftchild=parent*2+1 rightchild=parent*2+2
e~g
- 在具有2n个结点的完全二叉树中,叶子的结点个数为
解 在完全二叉树中有且只有3种情况
-
度为0
度为0,即只有根结点 叶子的结点个数也为n -
有且只有一个度为1的结点

设 x等于读为2的结点数 ,y等于叶子节点数 x+y+1=2n 又由叶子数等于度为2的加1得 y=x+1
得 y=n -
没有度为1的结点

由图可知 显然不能构成偶数个结点 故舍弃。
综上所述:叶子节点个数为n
一个具有完全二叉树的节点数为531个,那么这棵树的高度是
解: 直接带公式得 10;
一个具有767个结点的完全二叉树,其叶子节点个数为。
解 由前面的结论可知 此二叉树必定是
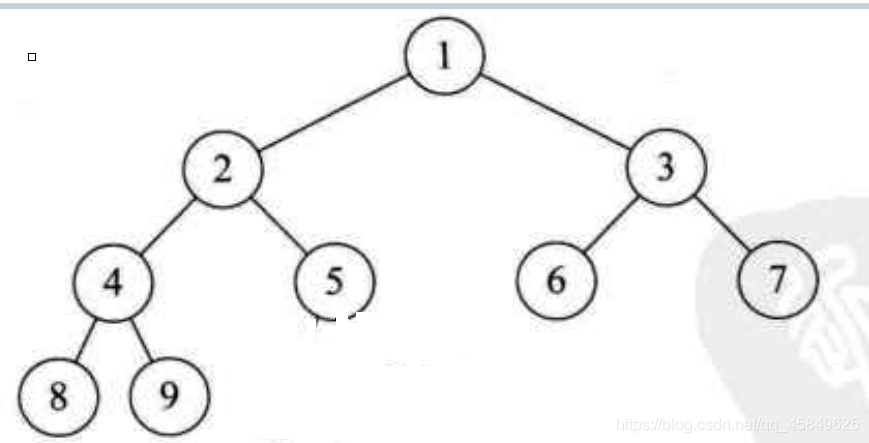
所以 设双结点为x 叶子为y y=x+1 且 y+y-1=767 解得 y=384
一颗度为2的树和二叉树有什么区别
解:
- 度为2的树是无序树 不区分左右 ,而二叉树必须先左后右。
- 度为2的树 一定有一个结点度为2,二叉树可以没有
证明 一个满k叉树上的叶子结点数n0和非叶子结点数n1瞒住*n0=(k-1)n1+1
首先,我们知道了满二叉树 ,满k叉树就是第n层以上的所有个结点的度都为k
总分支结点数=k倍的n1
总结点数=n0+n1
总分支结点数+1=总结点数
kn1+1=no+n1
二叉树的存储结构
二叉树的存储是按照自上而下,从左往右的排序的
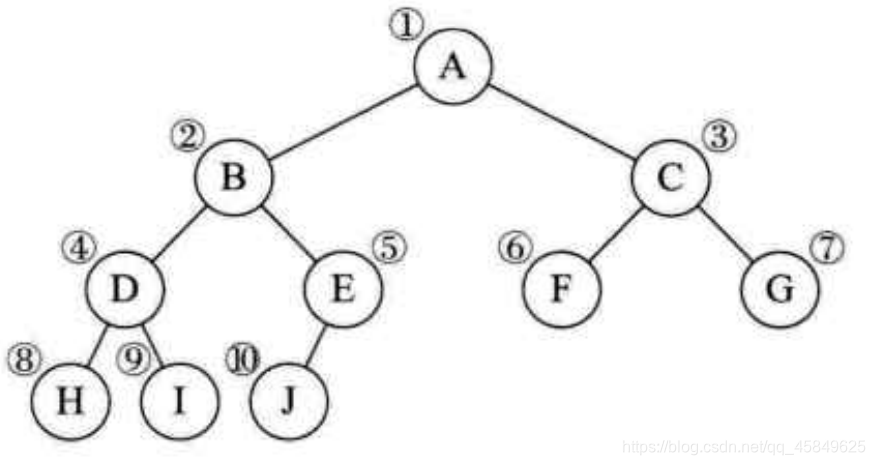
如果将该二叉树存入数组中 就会得到


二叉树与堆
堆是一种特殊的数,即是完全二叉树。
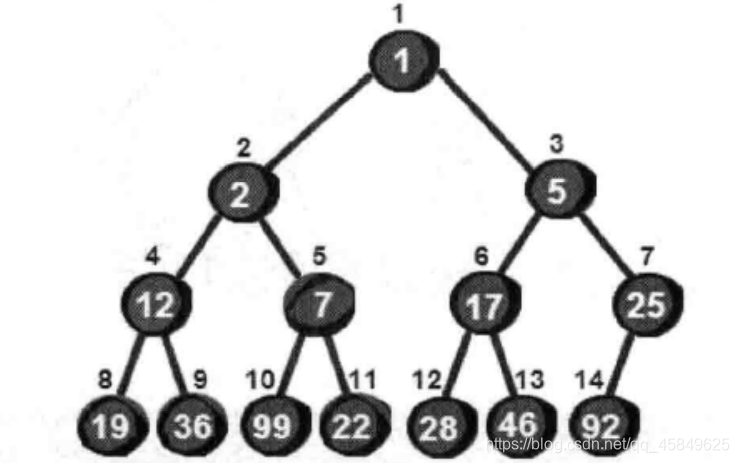
观察这个树 他的父结点都小于子结点,我们称之为最小堆,反之如果所有的父结点都比子结点大,这样的完全二叉树就被成为最大堆
注意:
- 堆是一颗完全二叉树
- 堆只有大堆和小堆两种
- 每个子树都是堆
堆的实现
有如下数组
int arr[] = { 23,2,5,12,7,17,25,19,36,99,22,28,46,92 };
如何将其调整成最小堆呢?
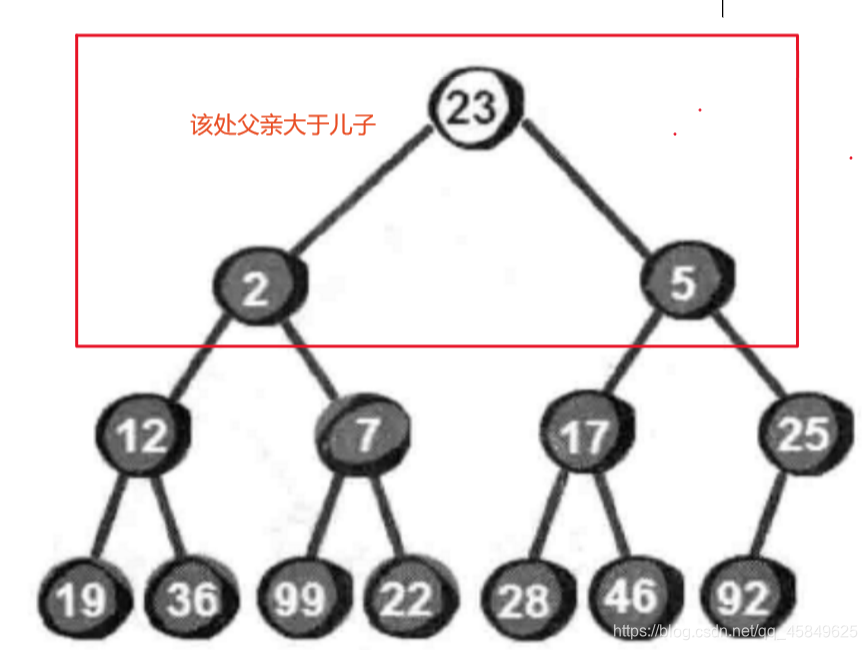
由图可知,最小堆的特点就是父亲小于儿子 ,而此树圈起来的地方儿子大于父亲,所以我们需要把最小的儿子换上去。

换下来后 我们发现还是不满足 所以还得交换
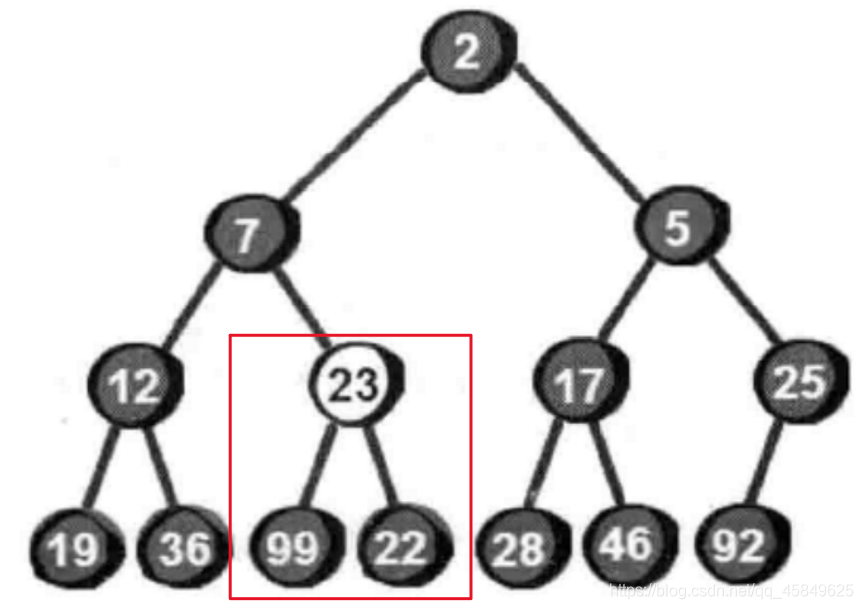
画圈处该二叉树任然不满足 只需要在交换一次,便是最小堆了

此时二叉树满足了最小堆。
此过程的算法,我们称之为向下调整算法,如果我们将一颗二叉树分区 即
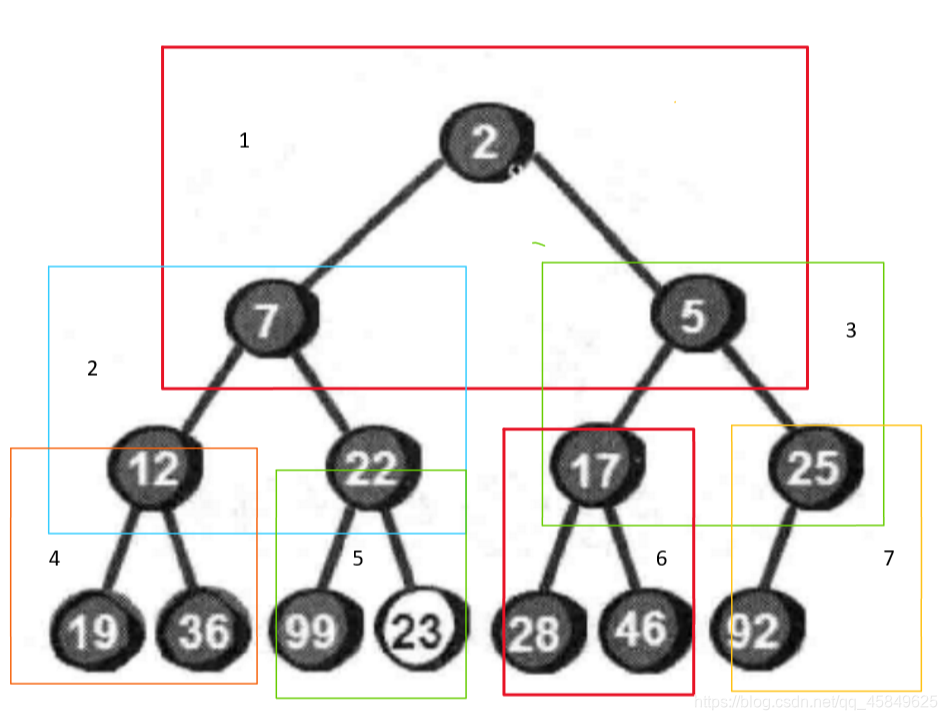
向下调整的本质就是先满足上面的,在满足下面的
注意:
- 向下调整算法,被调整元素的左右字树都必须是最小堆。
- 向下调整算法,调整到叶子结点时,即可停止
- 如果小的孩子比父亲打,则不需要处理,整个树已经是最小堆。
附上代码
#include<stdio.h>
void AdjustDown(int a[], int n, int parent)
{
int child = 2 * parent + 1;//套用公式可得
while (child < n)
{
if (child+1<n&&a[child] > a[child + 1])
{
child++;
}
if (a[parent] > a[child])
{
int tmp = a[child];
a[child] = a[parent];
a[parent] = tmp;
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
int main()
{
int arr[14] = { 23,2,5,12,7,17,25,19,36,99,22,28,46,92 };
int n = 14;
AdjustDown(arr, n, 0);
return 0;
}
代码解读




那么更一般的情况 左右子树都不是小堆的情况 ,怎么调整呢?
我们只需自下而上,由小的堆树变成大的堆树
即是 先满足下面在满足上面

先满足下面的堆 在满足上面 那么 只需要给函数依次传进去所有的父亲结点即可

#include<stdio.h>
void AdjustDown(int a[], int n, int parent)
{
int child = 2 * parent + 1;
while (child < n)
{
if (child+1<=n && a[child] >a[child + 1])
{
child++;
}
if (a[parent] < a[child])
{
int tmp = a[child];
a[child] = a[parent];
a[parent] = tmp;
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
int main()
{
int arr[14] = { 23,2,5,12,7,17,25,19,36,99,22,28,46,92 };
int n = 14;
int tmp = 0;
int i = (n - 1 - 1) / 2;
for (i; i >= 0; i--)
{
AdjustDown(arr, n, i);
}
return 0;
}
堆排序
以升序为例 ,我们首先会想到小堆 但是 小堆不适合。我们看
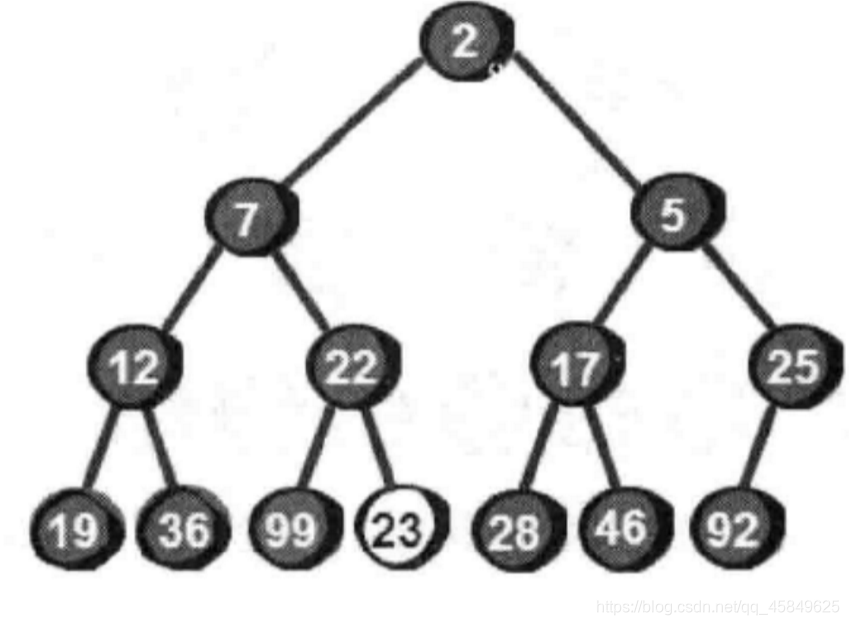
我们知道 堆顶元素一定是最小的 那么我们只需要依次拿走堆顶
当我们拿走2 后 7成了堆顶 之后
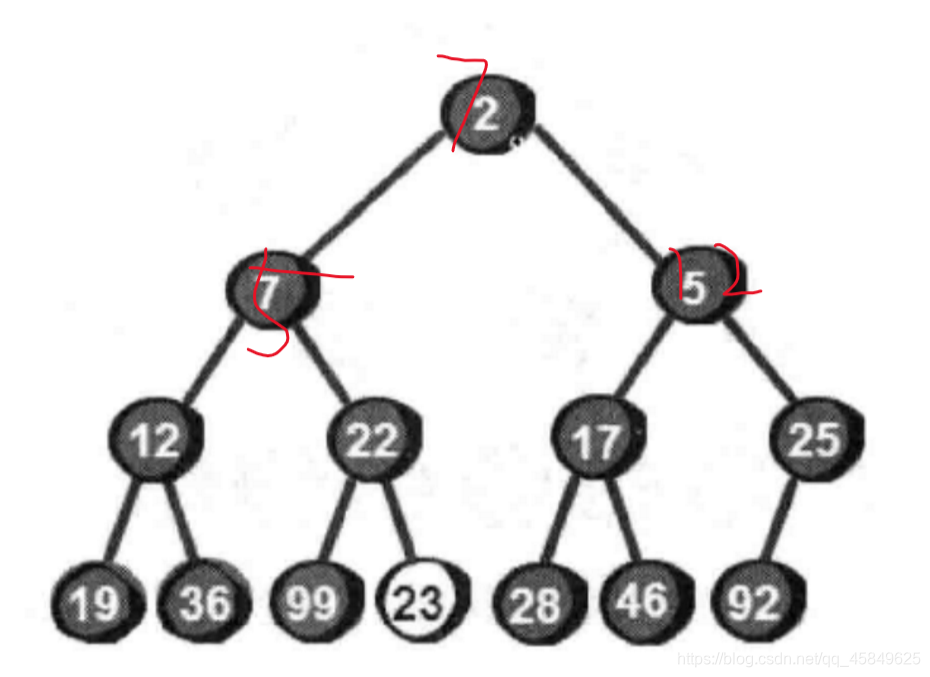
当去掉堆顶后 下一个元素补上 小堆荡然无存,顺序全乱了 。所以,小堆不适合排升序。
大堆排升序又该怎么办呢?
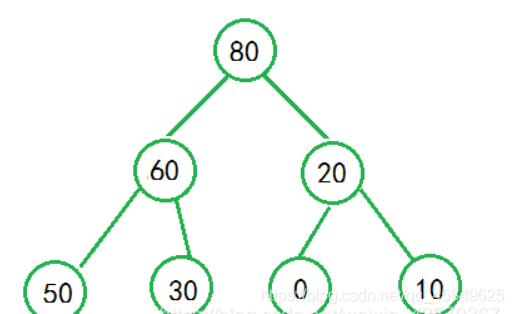
此时 ,我们只需要把10和80互换,不把80考虑在堆内

那么代码实现又当如何呢?

附上整体代码
#include<stdio.h>
void AdjustDown(int a[], int n, int parent)
{
int child = 2 * parent + 1;
while (child < n)
{
if (child+1<n && a[child] <a[child + 1])
{
child++;
}
if (a[parent] < a[child])
{
int tmp = a[child];
a[child] = a[parent];
a[parent] = tmp;
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
int main()
{
int arr[14] = { 23,2,5,12,7,17,25,19,36,99,22,28,46,92 };
int n =14 ;
int tmp = 0;
int i = (n - 1 - 1) / 2;
for (i; i >= 0; i--)
{
AdjustDown(arr, n, i);
}
int end = n - 1;
while (end > 0)
{
int tmp = arr[0];
arr[0] = arr[end];
arr[end] = tmp;
AdjustDown(arr, end, 0);
end--;
}
return 0;
}
堆排序是一种高效的排序
堆的总结:
- 物理结构是一个数组
- 逻辑结构是完全二叉树
- 大堆与小堆关系
- 堆排序
- 插入元素
- 快速找出最大或最小
堆的功能实现
堆的插入
堆的插入,要求插入之后还是堆。 这里我们引入堆的向上调整
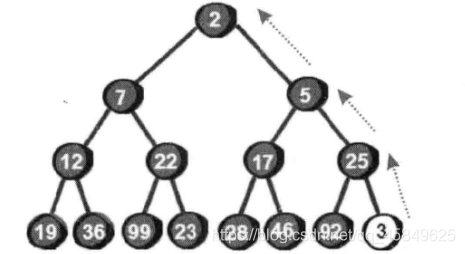
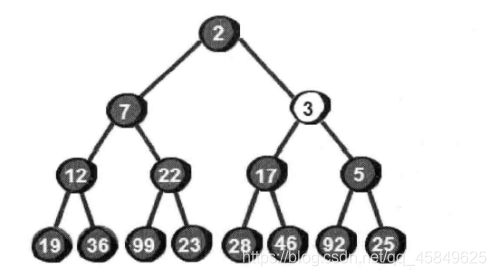
那么代码如何实现呢? 和向下排序类似
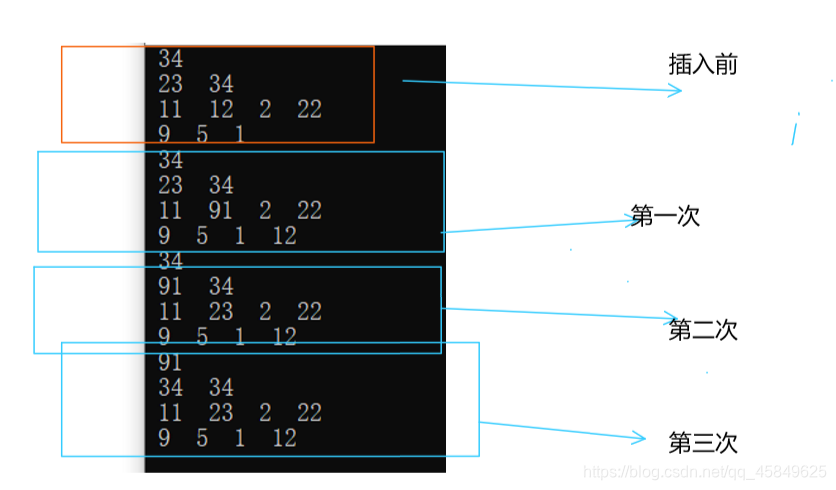
附上代码
void AdjustUp(int* a, int n, int child)
{
int parent = (child - 1) / 2;
while (child>0)
{
if (a[parent] < a[child])
{
Swap(&a[parent], &a[child]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
插入元素后经过一次向上排序即可。
也可以使用向下排序 但麻烦许多。
TOPK问题
TopK问题的本质就是取小堆取顶操作 建堆 ,然后取顶,甚至你可以说就是一个排顺序。把前四个放进别的数组。但是排序就意味着时间复杂度的加重 , 请读者使用建堆知识,取堆顶数据的方式,拿到最小数据, 这里给出题目和答案

* Note: The returned array must be malloced, assume caller calls free().
*/
/* 交换 */
void swap(int* a, int* b) {
int tmp = *a;
*a = *b;
*b = tmp;
}
/* 从堆下层向上交换元素,使得堆为大根堆 */
void swim(int* nums, int k) {
while (k > 1 && nums[k] > nums[k / 2]) {
swap(&nums[k], &nums[k / 2]);
k /= 2;
}
}
/* 从堆上层向下层交换元素,使得堆为大根堆 */
void sink(int* nums, int k, int numsSize) {
while (2 * k < numsSize) {
int child = 2 * k;
if (child < numsSize && nums[child] < nums[child + 1]) {
child++;
}
if (nums[k] > nums[child]) {
break;
}
swap(&nums[k], &nums[child]);
k = child;
}
}
/* 定义堆的结构体 */
typedef struct Heap {
int* data;
int szie;
int capacity;
}T_Heap, *PT_Heap;
/* 初始化一个堆 */
PT_Heap createHeap(int k) {
PT_Heap obj = (PT_Heap)malloc(sizeof(T_Heap));
obj->data = (int*)malloc(sizeof(int) * (k + 1));
obj->szie = 0;
obj->capacity = k + 1;
return obj;
}
/* 判断堆是否为空 */
bool isEmpty(PT_Heap obj) {
return obj->szie == 0;
}
/* 获得堆的当前大小 */
int getHeapSize(PT_Heap obj) {
return obj->szie;
}
/* 将元素入堆 */
void pushHeap(PT_Heap obj, int elem) {
/* 新加入的元素放入堆的最后 */
obj->data[++obj->szie] = elem;
/* 对当前堆进行排序,使其成为一个大根堆 */
swim(obj->data, obj->szie);
}
/* 获得堆顶元素 */
int getHeapTop(PT_Heap obj) {
return obj->data[1];
}
/* 将堆顶元素出堆 */
int popHeap(PT_Heap obj) {
/* 保存堆顶元素 */
int top = obj->data[1];
/* 将堆顶元素和堆底元素交换,同时堆长度减一 */
swap(&obj->data[1], &obj->data[obj->szie--]);
/* 将原先的堆底元素赋值为INT_MIN */
obj->data[obj->szie + 1] = INT_MIN;
/* 从堆顶开始重新堆化 */
sink(obj->data, 1, obj->szie);
return top;
}
int* getLeastNumbers(int* arr, int arrSize, int k, int* returnSize){
/* 若数组为空、或k为0,返回NULL */
if (arrSize == 0 || k == 0) {
*returnSize = 0;
return NULL;
} else {
*returnSize = k;
}
/* 返回数组长度为k */
int* ret = (int*)calloc(k, sizeof(int));
/* 初始化一个大小为k的堆 */
PT_Heap heap = createHeap(k);
/* 将输入数组前k个元素堆化 */
for (int i = 0; i < k; i++) {
pushHeap(heap, arr[i]);
}
/* 将输入数组剩下的元素依次插入堆,得出最小的k个数 */
for (int i = k; i < arrSize; i++) {
if (arr[i] < getHeapTop(heap)) {
popHeap(heap);
pushHeap(heap, arr[i]);
}
}
/* 将堆中元素传入返回数组 */
for (int i = 0; i < k; i++) {
ret[i] = popHeap(heap);
}
return ret;
}
二叉树的结构以及实现
二叉树的遍历
-
先序遍历
若二叉树为空,则空操作;否则
访问根节点;
先序遍历左子树
先序遍历右子树; -
中序遍历
若二叉树为空,则空操作;否则
中序遍历左子树
访问根节点;
中序遍历右子树;
- 后序遍历
后序遍历左子树
后序遍历右子树;
访问根节点;
代码实现
void PrevOrder(BTNode* root)
{
if (root == NULL)
{
printf(" NULL ");
return;
}
printf(" %c ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL");
return;
}
InOrder(root->left);
printf(" %c ", root->data);
InOrder(root->right);
}
void PostOrder(BTNode* root)
{
const BTNode* a = root;
if (root == NULL)
{
printf(" NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf(" %c ", root->data);
}
程序实现方法 以及递归小技巧
- 递归先确定你要递归的函数的功能 比如:他返回什么,他传入什么,他干了什么
- 分情况讨论 尽可能分清楚。
- 设计好函数出口
以本题为例
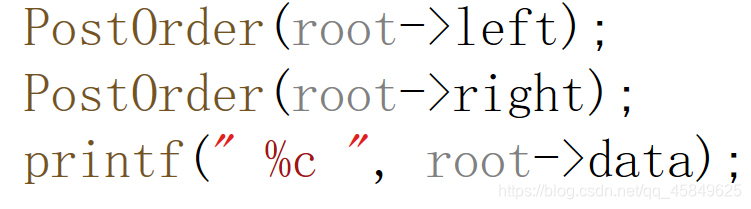
只要这三行代码 顺序变化 那么遍历方式也变化,这是为什么呢。
首先 函数的出口为root为空 而PostOrder(root->left);则是一直往左子树方向走,走到什么时候进行下一句呢? 走到底,走到底之后 就如图

此时根据函数出口,return ; 回回到上一层 如图
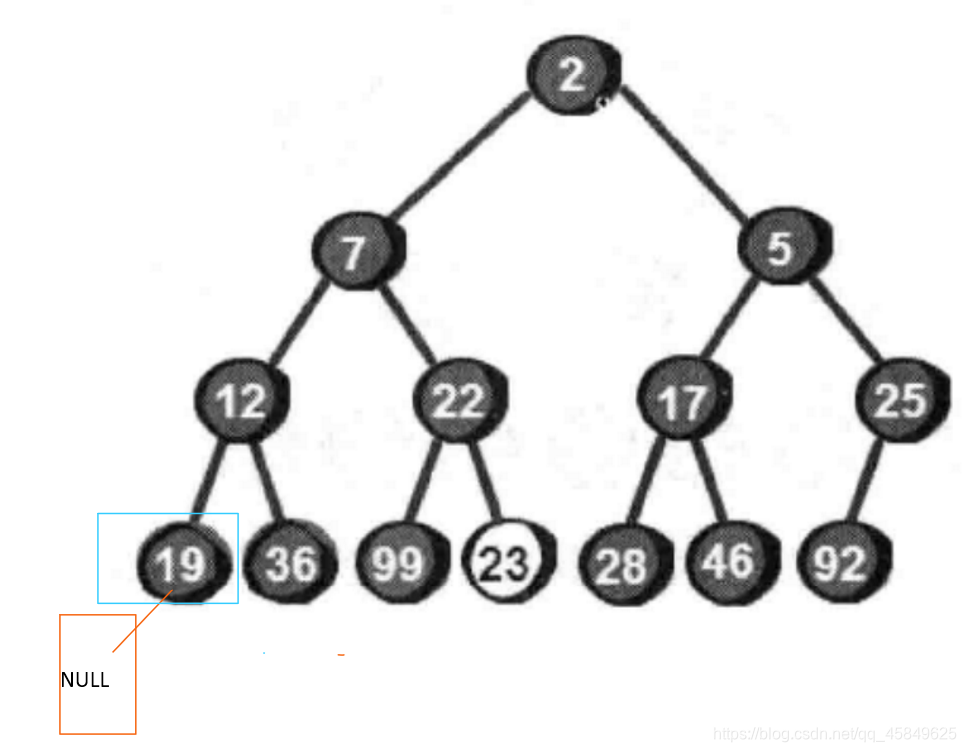
此时进入 PostOrder(root->right); 如图
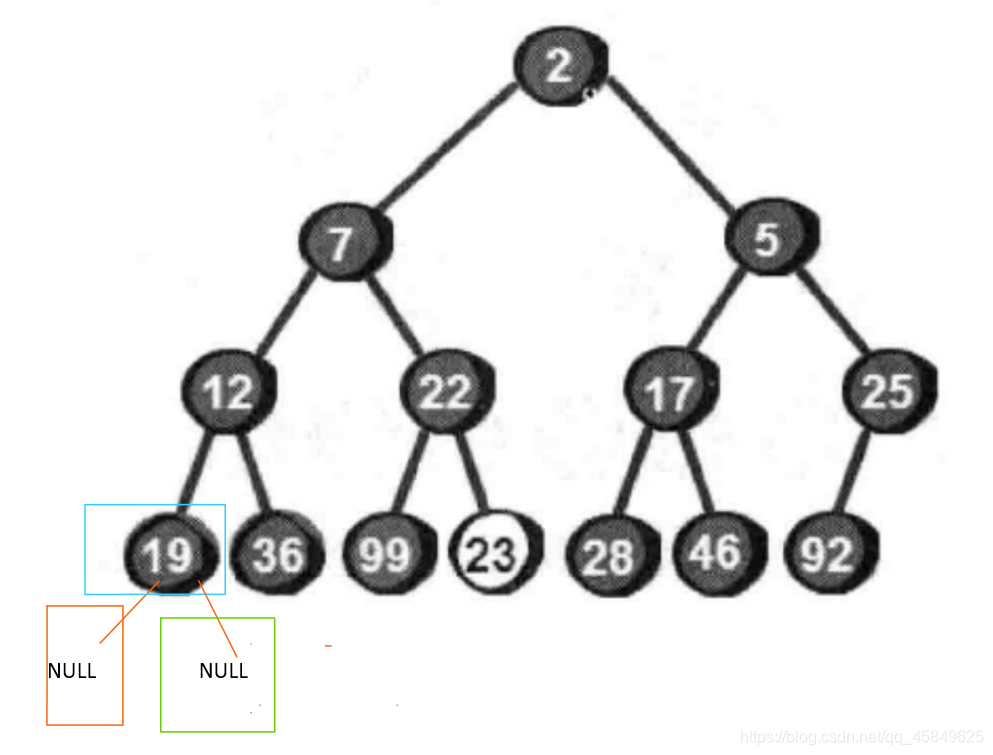
此时又满足了 函数出口 返回上一层 回到 19 往下走 打印 如此往复 我们得出结论,遍历只需要换即可。