《A self-learning genetic algorithm based on reinforcement learning for flexible job shop scheduling problem》
Computers & Industrial Engineering/2021

论文出发点:传统求解方法的关键参数不能动态调整导致求解效率和求解速度不能达到预期效果。
方法:用强化学习(SARSA算法和Q学习)优化参数 。
1 基本算法
1.1 遗传算法
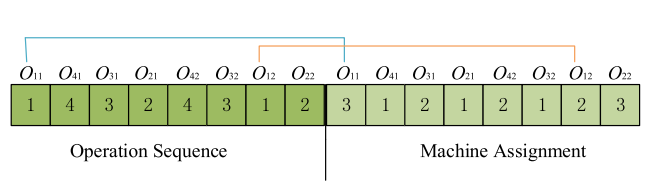
编码:MS、OS
初始化:随机
交叉:POX
选择:elite retention strategy
1.2 强化学习
强化学习的模型框架如下:

如下式如式,Agent会找到一个策略使得Reward最大:

Sarsa算法和Q-learning算法式两种类型值函数的强化学习算法,这两种算法的目标都是评估Q值,Q值保存在Q表中,初始Q表为零矩阵:

Sarsa的Q值更新公式如下所示:
![]()
Q-learniing的Q值更新公式为:
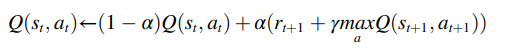
Q(St,at)是在状态St下采取行动at时的Q值,r为reward(奖励)。

2 SLGA(self-learning genetic algorithm,自适应遗传算法)

遗传算法中交叉变异算子十分重要,影响交叉变异最大的因素是Pc(交叉因子)、Pm(变异因子)。这两个过大会破坏较好的种群,较小,不容易产生新的好的个体。
这篇论文就是对pc,pm进行自适应控制。
2.1 组合模型(Combined model)
强化学习的要素主要有:策略、奖励、值函数和环境。
这些要素在GA和RL的组合模型中的体现如下图:

在SLGA中,action用来调整和更新Pc、Pm,然后GA使用更新后的Pc、Pm。然后再次进行交叉变异,GA的状态St变成St+1,然后,

2.2 建立学习模型

强化学习过程中,不同的阶段运用不同的算法,选择使用的阶段如下:

迭代前期用Sarsa,后期用Q-learnin.


2.3 State set(状态集)

其中,f(xi)表示染色体xi对应的适应度值(最大完工时间)
w1+w2+w3=1,这里设置为0.35,0.35,0.3.
state多可以使自适应学习更准确,但这也需要更多的探索,太少会导致结果不好,因此,这篇文章的State集划分成20个状态
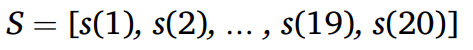
![]()
2.4 动作集(Action set)

2.5 奖励方法
更新Pc的Agent的奖励方法按照下列式子:
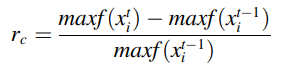
更新Pm的Agent的奖励方法按照下列式子:
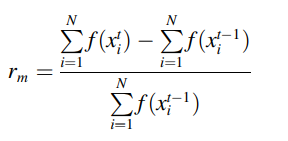
2.6 动作选择策略(她用的是 -greedy)
-greedy)
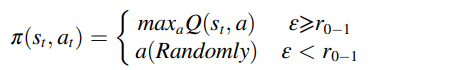
2.7 算法流程


3 实验
他采样用两种标准数据:Kacem's FJSP data,也就是(10×10)这些,和Branimarte标准数据(也就是mk01-mk10)
3.1 混合学习策略的实验对比(这里指Q-learning和Sarsa)
SLGA,GA-SARSA、GA-Q,GA之间的对比
参数设置:

性能指标:BSL、ASL、BKS分别为最优、平均、最差完工时间

RPD衡量解的分散度。
mk01-mk10的对比结果:


可以看到,SLGA是计算速度最快的,因为设置了更合适的交叉变异参数,所以冗余的交叉变异操作就减少了,同时质量也能得到保证。
下表为平均交叉变异的数量,SLGA交叉变异次数最少,这也是为什么运算速度快的原因:

从箱型图可以看出,SLGA的分散度最好

下表的对表4进行了统计分析,发现SLGA比其他算法的有更好的驱中趋势

下图为mk08的迭代曲线图

结论:

3.2 与其他算法比较



接着这篇论文进行了显著性分析对比SLGA和其他6种算法。——Friedman test(非参数检验)


