C语言中的二分查找(折半查找)
放在最前面的1、什么是二分查找(折半查找)?2、查找过程3、算法要求4、代码展示(举一个常见的例子)5、 输出结果(1)查找 7(2)查找 10(3)查找 20 6、 原理图展示7、总结(1)二分查找(折半查找)的优点:(2)二分查找(折半查找)的缺点: 8、END
放在最前面的
? ? 我的CSDN主页:OTWOL的主页,欢迎!!!????
??我的C语言初阶合集:C语言初阶合集,希望能帮到你!!!? ?
????创作不易,欢迎大家留言、点赞加收藏!!! ???
1、什么是二分查找(折半查找)?
二分查找 也称 折半查找(Binary Search),它是一种效率较高的查找方法。
用于在有序数组 或 有序列表中快速定位目标元素的位置。
它通过将目标值 与 数组中间元素进行比较,
从而将查找范围缩小一半,
不断迭代直到找到目标元素或确定目标元素不存在。
2、查找过程
1、确定查找范围:首先,确定要查找的有序数组或列表,并设置初始查找范围,通常是整个数组。
2、计算中间位置:计算查找范围的中间位置,可以使用 (左边界 + 右边界) / 2 的方式来获得中间位置。
3、比较目标值:将目标值与中间位置的元素进行比较。
(情况1)如果目标值等于中间位置的元素, 则找到目标元素,返回 中间位置。 (情况2)如果目标值小于中间位置的元素, 则目标元素可能在左半部分, 更新右边界为中间位置减一。 (情况3)如果目标值大于中间位置的元素, 则目标元素可能在右半部分, 更新左边界为中间位置加一。4、更新查找范围:根据比较结果更新查找范围,
将左边界或右边界移动到新的位置。
5、重复迭代:重复 步骤 2 到 步骤 4 ,
直到找到目标元素或确定目标元素不存在。
如果左边界大于右边界,表示目标元素不存在。
3、算法要求
1.必须采用顺序存储结构。2.必须按 元素 大小进行有序排列。4、代码展示(举一个常见的例子)
// void 表示 该函数 erfen 的返回值是 void (空)void erfen(int a){//定义一个整型变量 falg ,用于标记是否找到 aint flag = 0;//定义一个大小为 10 的一维数组 arr,里面存放着 1 ~ 10int arr[10] = { 1,2,3,4,5,6,7,8,9,10 };//定义一个整型变量 left ,用于存放左边界int left = 0;//定义一个整型变量 len ,用于存放数组的长度//sizeof 是操作符//用来计算变量的大小的int len = sizeof(arr) / sizeof(arr[0]);//定义一个整型变量 right ,用于存放右边界int right = len - 1;//定义一个整型变量 mid,存放与查找 数字 a进行判断的 数组的下标值int mid = (left + right) / 2;// while 循环while (left <= right){//数组 中间位置 的数值 < 要查找的 aif (arr[mid] < a){//数组的 左边界 left 被赋值为 mid + 1 left = mid + 1;}//数组的 中间位置 的数值 > 要查找的 aelse if(arr[mid] > a){//数组的 右边界 right 被赋值为 mid - 1 right = mid - 1;}//只剩下一种情况了//数组的 中间位置 的数值 == 要查找的 aelse{//修改标记值flag = 1;//输出打印找到的结果printf("找到了,下标是%d\n",mid);//跳出 while 循环break;}//取中间值mid = (left + right) / 2;}//循环结束的判断if (flag == 0){//输出没有找到的结果printf("没有找到\n");}}int main(){//定义一个整型变量 k,存放要查找的数字int k = 0;//输出打印提示信息printf("请输入你要查找的数字:");//输入要查找的数字scanf("%d", &k);//调用函数 -- 二分查找函数erfen(k);return 0;}5、 输出结果
(1)查找 7
输出打印:找到了,下标是 6
(2)查找 10
输出打印:找到了,下标是 9
(3)查找 20
输出打印:没有找到
6、 原理图展示
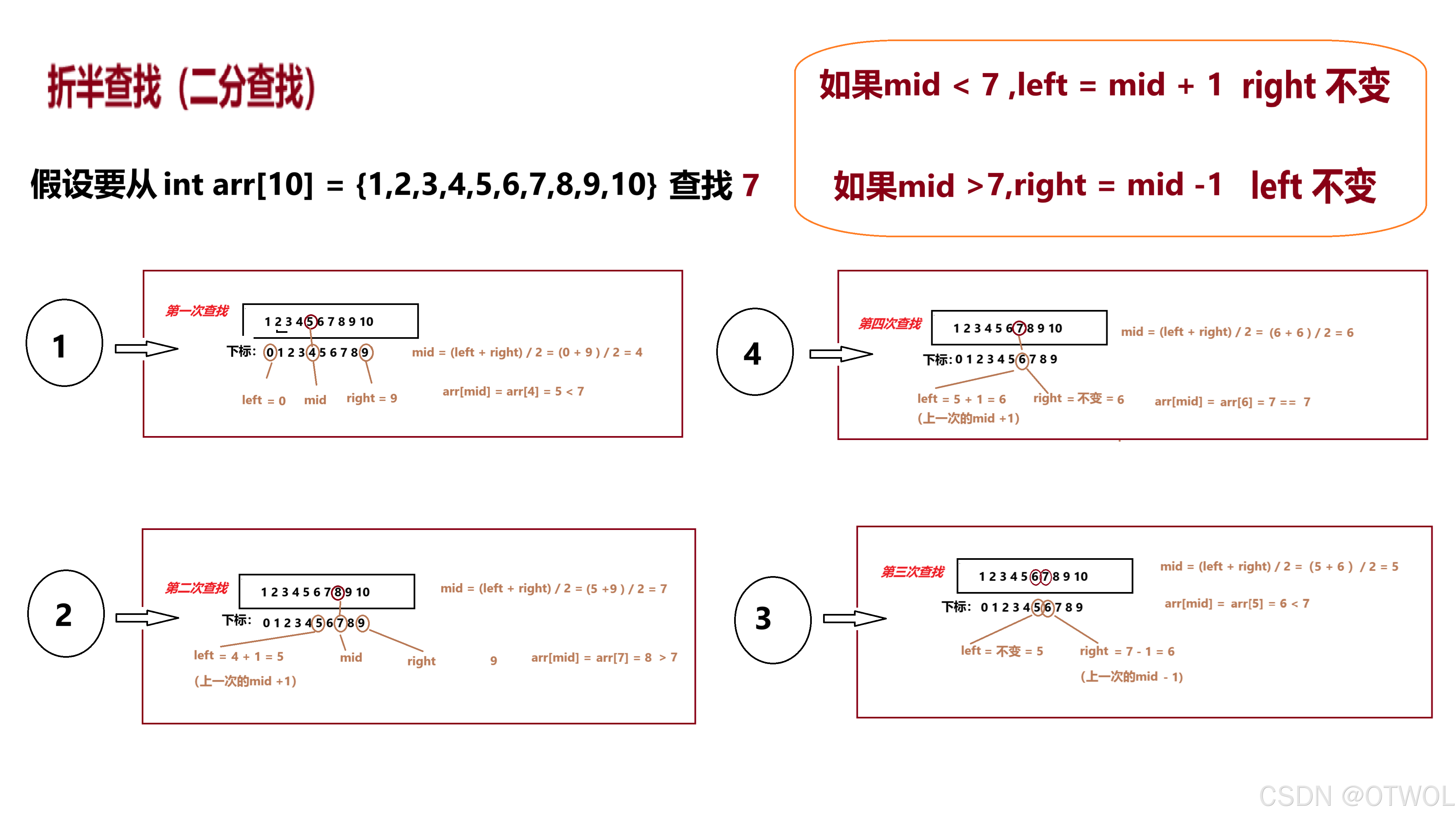
7、总结
(1)二分查找(折半查找)的优点:
1. 高效性:二分查找法的时间复杂度为O(log n),其中n为数组的大小。
相比于线性搜索算法的O(n)时间复杂度,二分查找法的效率更高。
在大规模数据集上,二分查找法能够快速定位目标元素。
2. 简单易实现:二分查找法的实现相对简单,
只需对有序数组进行适当的比较和范围缩小操作即可。
它不依赖于复杂的数据结构或算法,因此易于理解和实现。
3. 适用于静态数据集:二分查找法适用于静态数据集,
即不需要频繁地对数据集进行插入、删除操作的场景。
一旦有序数组建立,二分查找法可以多次重复利用,提高了效率。
4. 可用于非线性数据结构:二分查找法并不仅限于数组,
也可以应用于其他有序非线性数据结构,如有序链表、二叉搜索树等。
它在这些数据结构中同样具有高效性和简单性。
5. 可以定位目标元素位置:二分查找法不仅可以判断目标元素是否存在,
还可以确定目标元素的位置。通过返回目标元素所在的索引,
可以方便地进行后续操作,如数据的插入、删除等。
(2)二分查找(折半查找)的缺点:
1. 仅适用于有序数据集:二分查找法要求数据集必须是有序的,如果数据集无序,需要先进行排序操作,这增加了额外的时间和空间复杂度。
2. 需要连续的存储空间:二分查找法要求数据集能够通过索引进行随机访问,因此要求数据集在内存中具有连续的存储空间。对于链表等非连续存储的数据结构,无法直接应用二分查找法。
3. 不适用于动态数据集:如果数据集需要频繁进行插入和删除操作,二分查找法并不适用。因为每次插入和删除操作都会导致数据集的重新排序,破坏了有序性,需要重新建立索引。
4. 无法处理重复元素:二分查找法无法处理数据集中存在重复元素的情况。由于二分查找法只能找到一个目标元素的位置,无法区分相同值的不同元素。
5. 时间复杂度不适用于小规模数据集:虽然二分查找法的时间复杂度为O(log n),但在小规模数据集上,其实际运行时间可能比简单的线性搜索算法更长。这是因为二分查找法需要进行多次比较和索引调整,而线性搜索算法只需要遍历一次。
8、END
每天都在学习的路上!
On The Way Of Learning
