【MATLAB】FIR滤波器的MATLAB实现

FIR滤波器的MATLAB实现

FIR滤波器的设计fir1函数fir2函数

与IIR滤波器相比，FIR滤波器既有其优势也有其局限性。FIR滤波器的主要优点包括：

精确的线性相位响应；永远保持稳定性；设计方法通常是线性的；在硬件实现中具有更高的运行效率；启动传输仅需有限的时间。

然而，FIR滤波器也存在一些显著的缺点：

为了达到与IIR滤波器相同的性能要求，FIR滤波器通常需要更高的阶数；相应地，FIR滤波器的延迟时间比具备相同性能的IIR滤波器要高得多。

FIR滤波器的设计

MATLAB 信号处理工具箱提供了表1用于设计 FIR 数字滤波器的方法和工具函数。

设计方法	说明	工具函数
窗函数法	对理想滤波器进行加窗处理，并根据滤波器的性能指标截取某一段，以近似地实现理想滤波器	fir1, fir2, kaiserord
多带和过渡带	等波纹或者最小二乘法逼近频率范围内的子带	firls, firpm, firpmord
约束最小二乘法	满足最大误差限制条件下使整个频带平方误差最小化	fircls, fircls1
任意响应法	任意响应，包括非线性相位和复杂滤波器	cfirpm
升余弦法	具有光滑余弦过渡带的低通滤波器的设计	firreos

表1. FIR 数字滤波器设计方法和工具函数

窗函数法是设计FIR滤波器的重要方法之一，本文主要介绍FIR滤波器的窗函数设计方法。

在实际应用中，遇到的离散时间信号通常是有限长度的，因此在信号处理中不可避免地会遇到数据截短的问题。对于离散序列的截短，可以通过序列与窗函数的相乘来实现。

常用的窗函数包括矩形窗、巴特利特（Bartlett）窗、三角窗、海明（Hamming）窗、汉宁（Hanning）窗、布莱克曼（Blackman）窗、切比雪夫（Chebyshev）窗和凯泽（Kaiser）窗。MATLAB信号处理工具箱提供了一组用于生成这些窗函数的函数，具体见表2。

函数	函数功能
w=bartlett(n)	生成巴特立特 ( Bartlett ) 窗
w=blackman(n)	生成布莱克曼 ( Blackman ) 窗
w=boxcar(n)	生成矩形窗
w=chebwin(n)	生成切比雪夫 ( Chebyshev ) 窗
w-hamming(n)	生成海明 ( Hamming ) 窗
w=hanning(n)	生成汉宁 ( Hanning ) 窗
w=kaiser(n)	生成凯泽 ( Kaiser ) 窗
w=triang(n)	生成三角窗
函数说明	n为窗的长度

表2. MATLAB 信号处理工具箱窗函数汇总

fir1函数

MATLAB信号处理工具箱提供了基于加窗的线性相位FIR滤波器设计函数 fir1 和 fir2。fir1 函数的调用语法如下：

b=fir1(n,Wn,'fype',window)

其中：

n 表示滤波器的阶数。ftype 表示所设计滤波器的类型，可选参数包括： high：高通滤波器stop：带阻滤波器DC-1：多通带滤波器，第一频带为通带DC-0：多通带滤波器，第一频带为阻带默认情况下，fir1 设计的是低通或带通滤波器。 window 为窗函数，是一个长度为 n+1 的列向量。默认情况下，函数自动使用 Hamming 窗。

例1. 设计一个48阶的FIR带通滤波器，通带范围为0.35≤w≤0.65。

clc;clear;closeb = fir1(48,[0.35 0.65]); % 调用fir1函数进行FIR带通滤波器设计freqz(b,1,512)            % 画出幅频和相频响应图

输出的频率响应特性如图1所示：

图1. FIR带通滤波器幅频特性

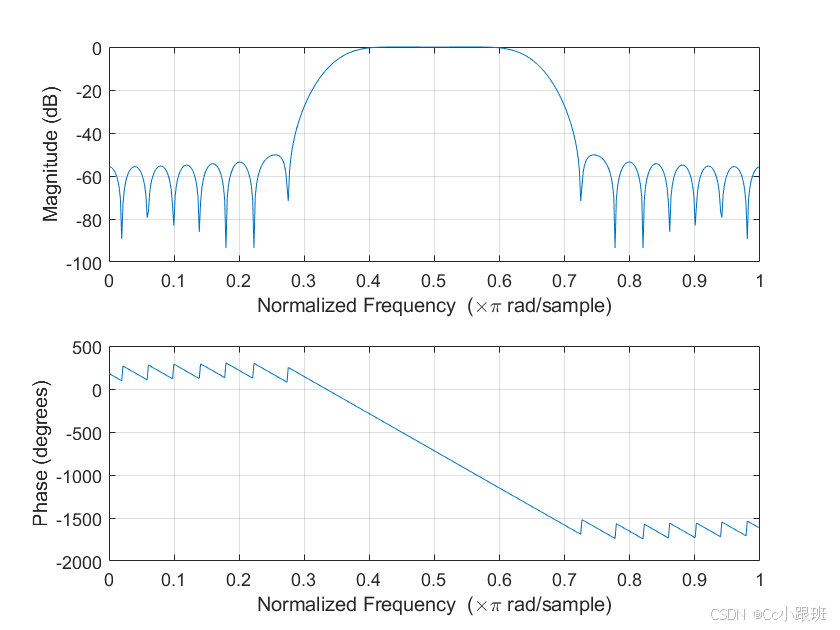
例2. 用窗函数法设计多通带滤波器，归一化通带为[0 0.2]、[0.4 0.6]、[0.8 1]。由于高频端为通带，因此滤波器的阶数应为偶数，这里定为40。

首先将通带要求用向量w来表示，然后调用fir1函数进行滤波器设计。

w=[0.2 0.4 0.6 0.8]; % 滤波器设计参数b=fir1(40,w,'dc-1'); % 用窗函数法设计多通带滤波器freqz(b,1,512)       % 绘制幅频-相频特性图

输出的幅频-相频特性如图2所示。

图2. 多通带滤波器幅频-相频特性

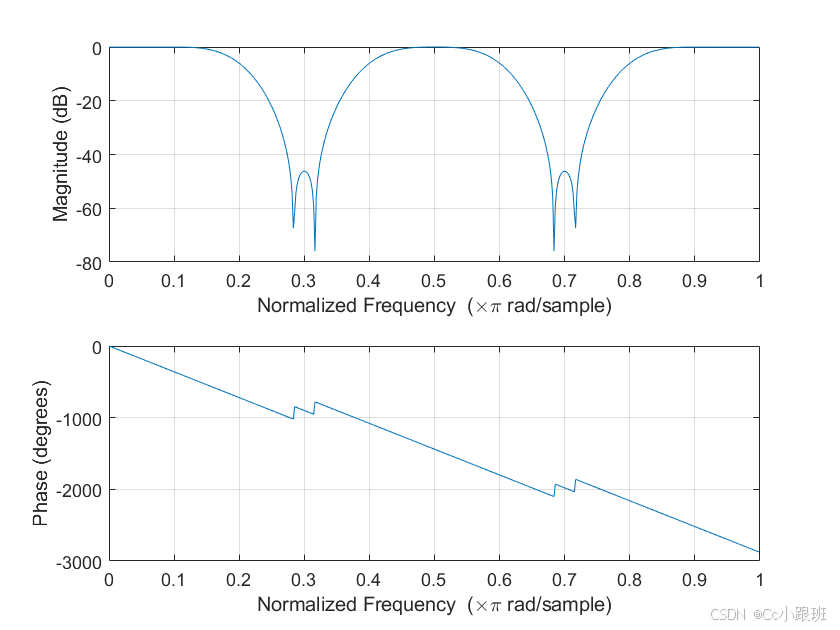
fir2函数

MATLAB信号处理工具箱提供了fir2函数，用于基于频率采样的有限冲激响应（FIR）滤波器设计。其调用语法如下：

b = fir2(n, f, m, npt, lap, window)

n：滤波器的阶数。f：频率向量，其取值范围在 [0, 1] 之间。m：幅度响应向量，其取值范围也在 [0, 1] 之间。npt：用于频率响应插值的点数，默认值为 512。lap：一个参数，用于指定 fir2 在重复频率点附近插入的区域大小。window：窗函数类型，其长度必须为 n + 1，默认使用 Hamming 窗。b 向量表示返回的滤波器系数。

例3. 设计一个50阶低通滤波器，并且绘制理想频率响应和实际频率响应图。

f=[0 0.6 0.6 1];m=[1 1 0 0];b =fir2(50,f,m);[h,w]=freqz(b,1,128);plot(f,m,w/pi,abs(h)) % 画出幅频和相频响应图legend('Ideal','fir2 Designed')title('Comparison of Frequency Response Magnitudes ')xlabel('Normalized Frequency(rad/sample)');ylabel('magnitude')

输出的频率响应特性如图3所示：

图3. 频率响应特性图


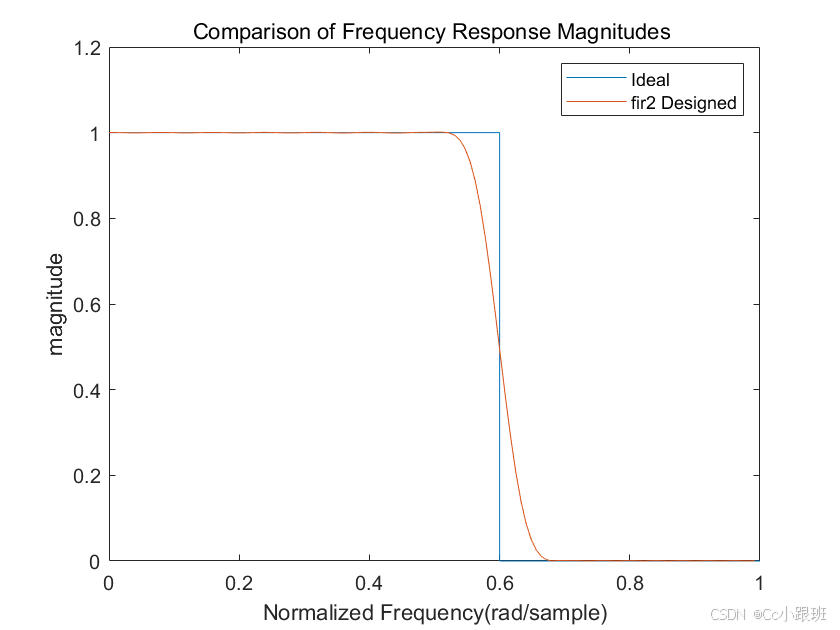
END
2024年9月6日