
本篇博客给大家带来的是排序的知识点, 由于时间有限, 分两天来写, 下篇主要实现最后一种排序算法: 归并排序。同时把中篇剩下的快排非递归实现补上.
文章专栏: Java-数据结构
若有问题 评论区见
欢迎大家点赞 评论 收藏 分享
如果你不知道分享给谁,那就分享给薯条.
你们的支持是我不断创作的动力 .
王子,公主请阅!!!
1. 快速排序的非递归实现1.1 具体实现1.1.1 区间入栈细节 1.2 代码如下: 1.3 快速排序的特性总结: 2. 归并排序 2.1 归并排序的基本思想2.2 具体步骤 2.2.1 分解操作 2.2.1 合并排序操作 2.3 归并排序的非递归实现2.4 归并排序的特性总结:
1. 快速排序的非递归实现
拿到第一个基准值pivot之后, 如何进行左右子序列的快速排序呢?
可以利用栈保存左区间 和 右区间.
1.1 具体实现
1. 利用上篇文章的 partition算法拿到第一个基准值,用栈存储左区间 和 右区间,
2. 重复第一步,直到栈为空.
1.1.1 区间入栈细节
如下分析图:
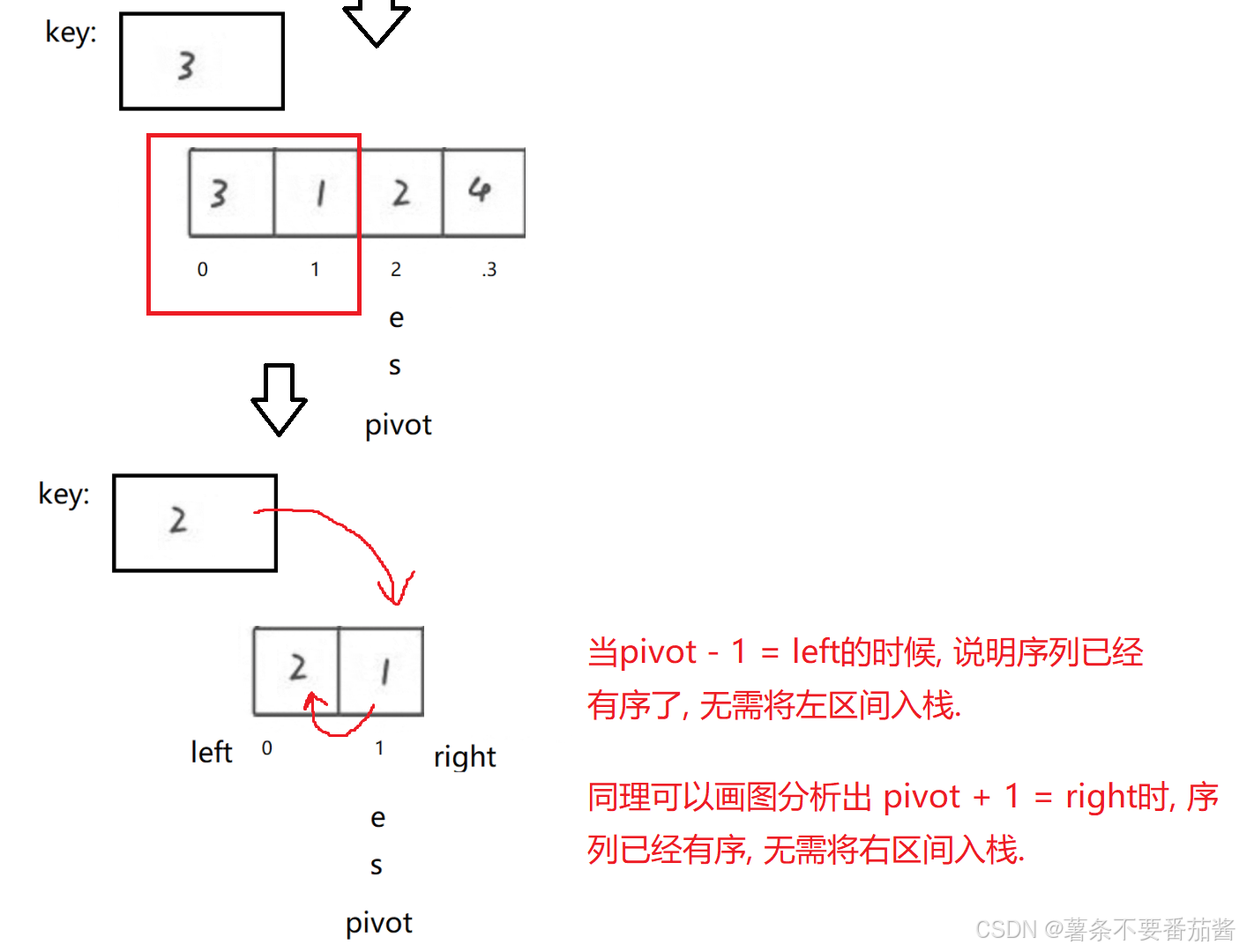
1.2 代码如下:
//挖坑法,求基准值.private static int partition2(int[] array,int left,int right) { int key = array[left]; while(left < right) { while(left < right && array[right] >= key) { right--; } //从右边开始第一个比key小的元素覆盖[left] array[left] = array[right]; while(left < right && array[left] <= key) { left++; } //从左边开始第一个比key大的元素覆盖空位. array[right] = array[left]; } //key填补最终的空位,此时left=right array[left] = key; return left; }//快速排序法的非递归实现. public static void quickSortNor(int[] array) { Stack<Integer> stack = new Stack<>(); int left = 0; int right = array.length-1; //拿到第一个基准 int pivot = partition2(array,left,right); //左序列区间端点入栈. if(pivot-1 > left) { stack.push(left); stack.push(pivot-1); } //右序列区间端点入栈. if (pivot+1 < right) { stack.push(pivot+1); stack.push(right); } while(!stack.isEmpty()) { right = stack.pop(); left = stack.pop(); pivot = partition2(array,left,right); if(pivot-1 > left) { stack.push(left); stack.push(pivot-1); } if (pivot+1 < right) { stack.push(pivot+1); stack.push(right); } } }1.3 快速排序的特性总结:
1. 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
2. 时间复杂度:O(N*logN)
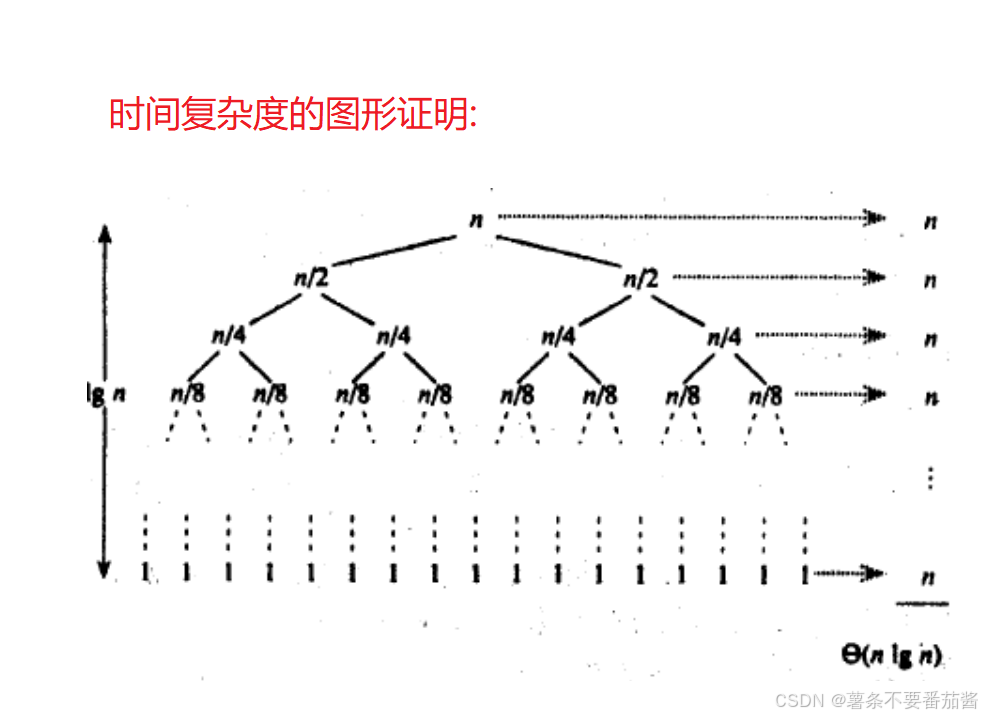
3. 空间复杂度:O(logN)
4. 稳定性:不稳定
2. 归并排序
2.1 归并排序的基本思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and
Conquer)的一个非常典型的应用。原序列分解成若干个子序列, 子序列排序, 将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
2.2 具体步骤
2.2.1 分解操作
定义left = 0, right = array.length-1; mid = (left + right)/2; 递归分解即可.[left,mid],[mid+1,right]; 注意递归的终止条件 left >= right.
/** * 归并排序 * 时间复杂度: O(N*logN) 和快速排序类似, * * 空间复杂度:O(N) - 临时数组和原数组长度一样. * * 稳定性: 稳定. * * @param array */public static void mergeSort(int[] array) { mergeSortFunc(array,0,array.length-1); } //先分解,再归并排序. private static void mergeSortFunc(int[] array,int left,int right) { if(left >= right) return; int mid = (left+right)/2; //分解左右 mergeSortFunc(array,left,mid); mergeSortFunc(array,mid+1,right); //将小数组排序合并 merge(array,left,mid,right); }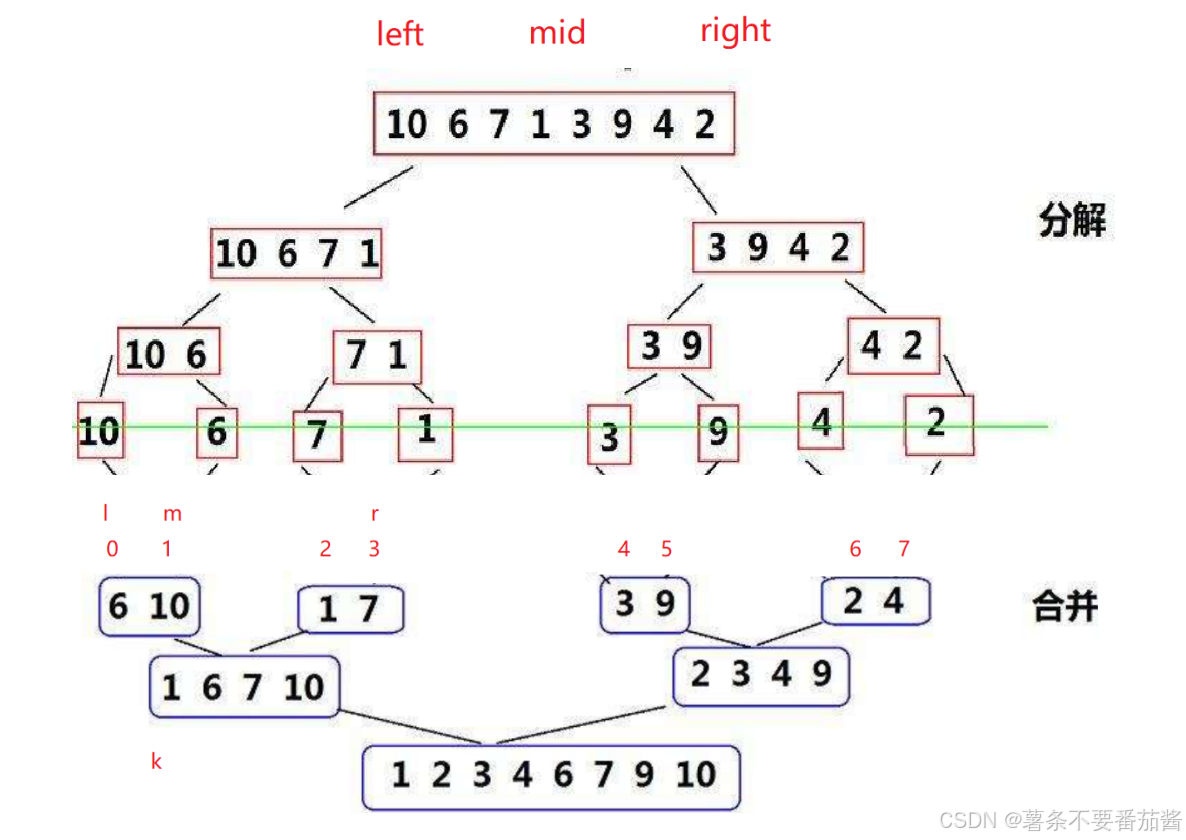
2.2.1 合并排序操作
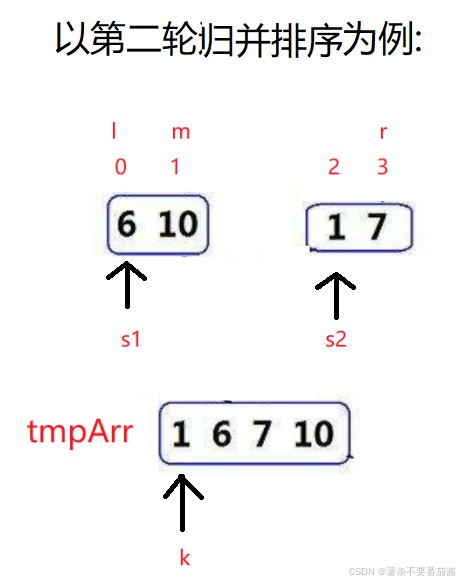
1. 定义一个临时数组,用来存放有序的子序列,长度为 right - left + 1, k 指向数组起始位置; 令s1指向[left],s2指向[mid+1].
2. [s1] 与 [s2] 比较, 若[s1] > [s2], 则 [s2] 放到数组中, s2++, [s2] < [s1]…类推
3. 重复第二步 直到 s1 > mid && s2 > right.
4. s1 与 s2 中两边的元素总有一边先放完, 把剩下的那边元素放入临时数组即可.

5. 最后一步将有序的临时数组放回原数组.
//归并排序的核心 private static void merge(int[] array,int left,int mid,int right) { int s1 = left; int s2 = mid+1; int k = 0; int[] tmpArr = new int[right-left+1]; while(s1 <= mid && s2 <= right) { if(array[s2] <= array[s1]) { //等号不取便稳定. tmpArr[k++] = array[s2++]; }else { tmpArr[k++] = array[s1++]; } } //s1中所有元素都大于s2,s2放完了,s1还没放完. while(s1 <= mid) { tmpArr[k++] = array[s1++]; } //s2中所有元素都大于s1,s1放完了,s2还没放完. while(s2 <= right) { tmpArr[k++] = array[s2++]; } //tmpArr为有序数组. for (int i = 0; i < tmpArr.length; i++) { array[i+left] = tmpArr[i];//left不一定为0. } }2.3 归并排序的非递归实现
在归并排序核心算法的基础上, 定义变量gap = 1, 循环for (int i = 0; i < array.length; i += gap*2)中, left = i; mid = left+gap-1; right = mid+gap; 这么定义可以将原数组分为若干个长度为2的小数组.
由于要不断分解, 故gap应当写一个循环.
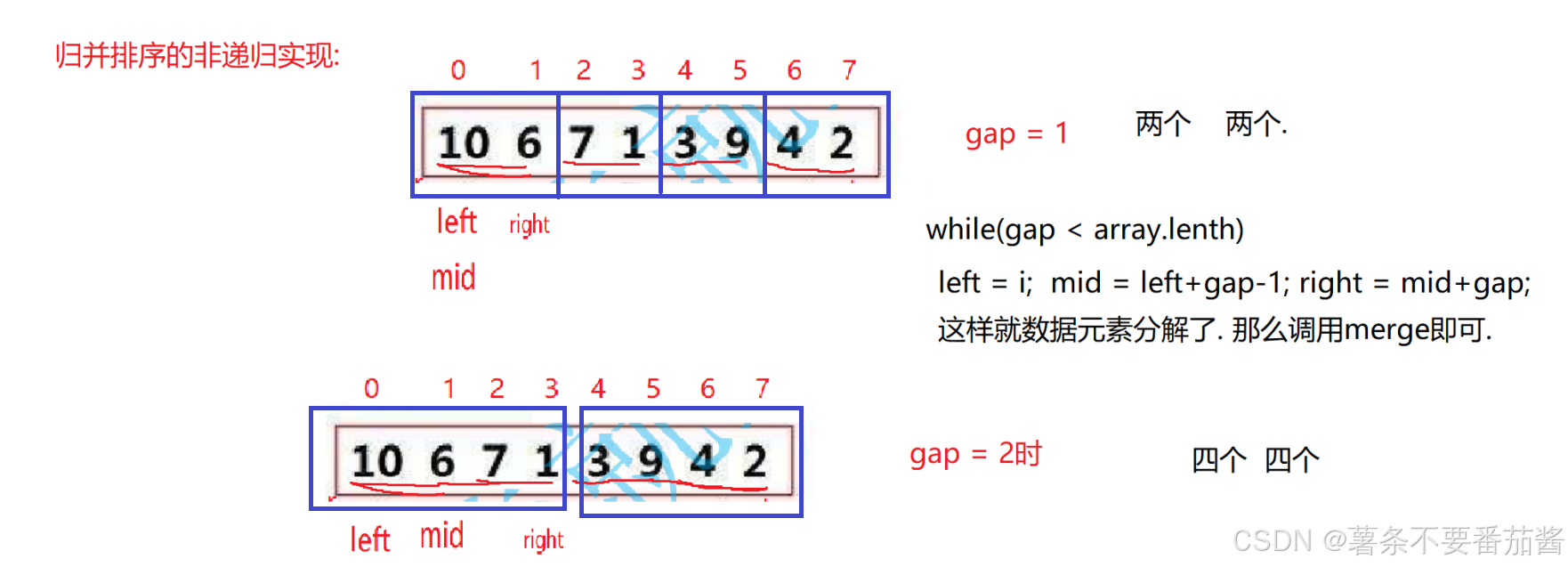
处理细节:
当gap > array.length/2时, mid和right可能会越界, 所以 需要加上条件,防止越界.
代码如下:
//归并排序的核心 private static void merge(int[] array,int left,int mid,int right) { int s1 = left; int s2 = mid+1; int k = 0; int[] tmpArr = new int[right-left+1]; while(s1 <= mid && s2 <= right) { if(array[s2] <= array[s1]) { //等号不取便稳定. tmpArr[k++] = array[s2++]; }else { tmpArr[k++] = array[s1++]; } } //s1中所有元素都大于s2,s2放完了,s1还没放完. while(s1 <= mid) { tmpArr[k++] = array[s1++]; } //s2中所有元素都大于s1,s1放完了,s2还没放完. while(s2 <= right) { tmpArr[k++] = array[s2++]; } //tmpArr为有序数组. for (int i = 0; i < tmpArr.length; i++) { array[i+left] = tmpArr[i];//left不一定为0. } } //归并排序的非递归实现. public static void mergeSortNor(int[] array) { int gap = 1; while(gap < array.length) { for (int i = 0; i < array.length; i += gap*2) { int left = i; int mid = left+gap-1; int right = mid+gap; //mid和right可能会越界 if(mid >= array.length) { mid = array.length-1; } if(right >= array.length) { right = array.length-1; } merge(array,left,mid,right); } gap *= 2; } }2.4 归并排序的特性总结:
1. 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度:O(N*logN) -> 算法与快排类似.
3. 空间复杂度:O(N) -> 临时数组长度与原数组相同.
4. 稳定性:稳定
总的来说, 快排和归并排序还是需要花时间去想清楚每一步是怎么回事, 代码为什么要这么写??? 去解答心里有十万个为什么, 解答出自己问自己的所有的问题, 就说明掌握了这个知识点.
本篇博客到这里就结束啦, 感谢观看, 期待与你的下一次相遇!!!