点一下关注吧!!!非常感谢!!持续更新!!!
目前已经更新到了:
Hadoop(已更完)HDFS(已更完)MapReduce(已更完)Hive(已更完)Flume(已更完)Sqoop(已更完)Zookeeper(已更完)HBase(已更完)Redis (已更完)Kafka(已更完)Spark(已更完)Flink(已更完)ClickHouse(已更完)Kudu(已更完)Druid(已更完)Kylin(已更完)Elasticsearch(已更完)DataX(已更完)Tez(已更完)数据挖掘(正在更新…)章节内容
上节我们完成了如下的内容:
机器学习理论 基础内容有监督、无监督、半监督、强化学习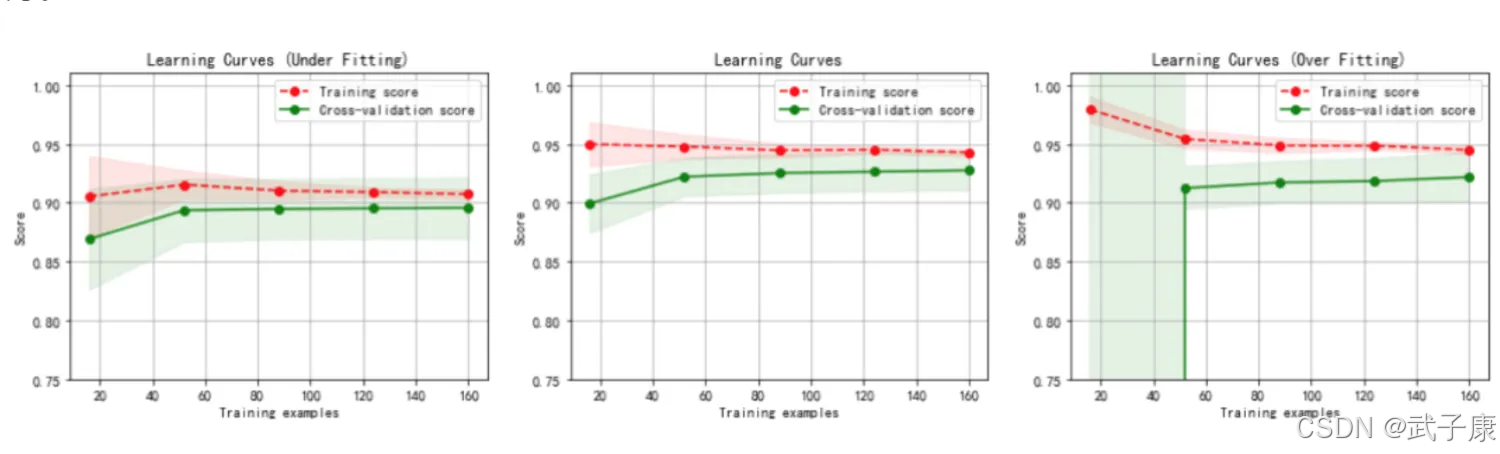
监督学习算法
KNN/K近邻算法
它的本质是通过距离判断两个样本是否相似,如果距离够近就认为他们足够相似属于同一个类别。
当然只对比一个样本是不够的,误差会很大,他们就需要找到离其最近的 K 个样本,并将这些样本称为【近邻】nearest neighbor,对这 K 个近邻,查看它们都属于任何类别(这些类别称为称为【标签】labels)。
实现过程
假设 X_test 待标记的数据样本,X_train 为已标记的数据集。
遍历已标记数据集中的所有样本,计算每个样本与待标记的点的距离,并把距离保存在 Distance 数组中。对 Distance 数组进行排序,取距离最近的 K 个点,记为X_knn。在 X_knn 中统计每个类别的个数,即 class0 在 X_knn 中有几个样本,class1 在 X_knn中有几个样本待标记样本的类别,就是在 K_knn 中样本个数最多的那类别。距离的确定
该算法的【距离】在二维坐标轴就表示两点之间的距离,计算距离的公式有很多。我们常说的欧拉公式,即“欧氏距离”,回忆一下,一个平面直角坐标系上,如何计算两点之间的距离?一个立体直角坐标系上,又如何计算两点之间的距离?
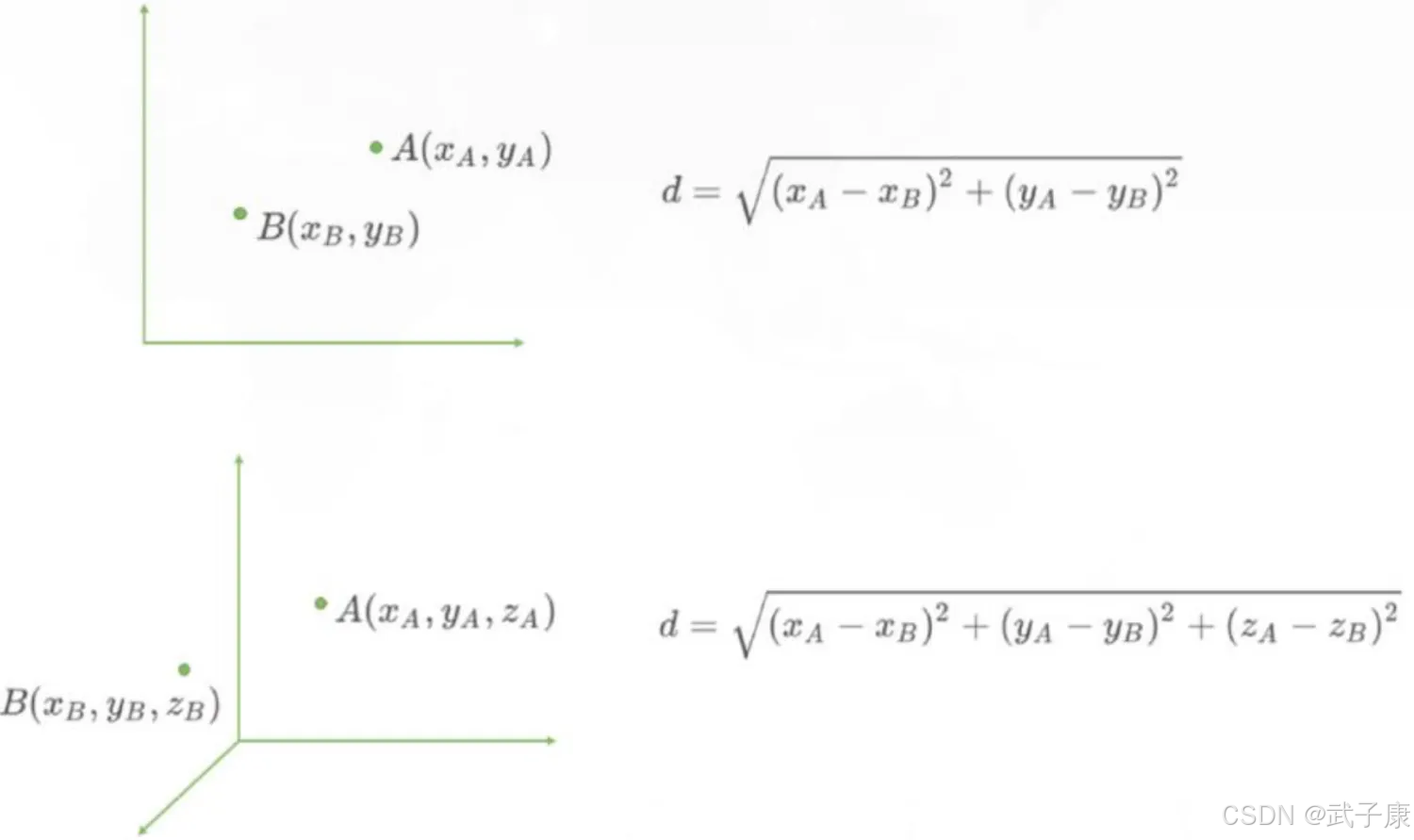
当特征数量有很多个形式多维空间时,再用上述的写法就不方便了,我们换一个写法,用 X 加下角标的方式表示特征维度,则在 N 维空间中,有两个点 A 和B,它们坐标分别为:

而在机器学习中,坐标轴上的 x1、x2、x3等,正是我们样本上的N 个特征。
算法优点
算法参数是k,k 可以理解为标记数据周围几个数作为参考对象,参数选择需要根据数据来决定。
k 值越大,模型的偏差越大,对噪声数据不敏感。k 值很大时,可能造成模型的欠拟合。k 值越小,模型的方差就会很大。但是 k 值太小,容易过拟合。算法变种
变种 1
默认情况下,在计算距离时,权重都是相同的,但实际上可以针对不同的领居指定不同的距离权重,比如距离越近权重越高。
可以通过指定算法的 weights 参数来实现。
变种2
使用一定半径内的点取代距离最近的 k 个点
在 scikit-learn 中,RadiusNeighborsClassifier 实现了这种算法的变种当数据采样不均匀时,该算法变种可以获得更好的性能代码实现
导入相关包
# 全部行都能输出from IPython.core.interactiveshell import InteractiveShellInteractiveShell.ast_node_interactivity = "all"import numpy as npimport pandas as pdimport matplotlib.pyplot as plt# 解决坐标轴刻度负号乱码plt.rcParams['axes.unicode_minus'] = False# 解决中文乱码问题plt.rcParams['font.sans-serif'] = ['Simhei']plt.style.use('ggplot')# plt.figure(figsize=(2,3),dpi=720)执行结果如下:
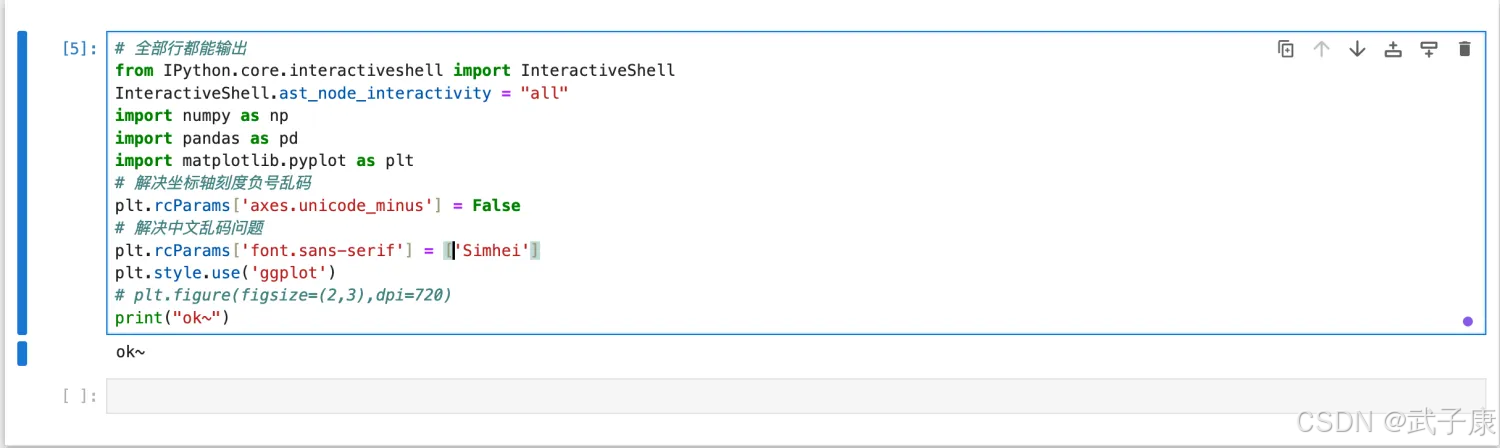
构建已经分类好的原始数据集
首先随机设置十个样本表示十杯酒,这里去了部分样本点。
为了方便验证,使用 Python 的字典 dict 构建数据集,然后再将其转换为DataFrame 格式。
rowdata = { '颜色深度': [14.13,13.2,13.16,14.27,13.24,12.07,12.43,11.79,12.37,12.04], '酒精浓度': [5.64,4.28,5.68,4.80,4.22,2.76,3.94,3.1,2.12,2.6], '品种': [0,0,0,0,0,1,1,1,1,1]}# 0 代表 “黑皮诺”,1 代表 “赤霞珠”wine_data = pd.DataFrame(rowdata)执行结果如下图所示:
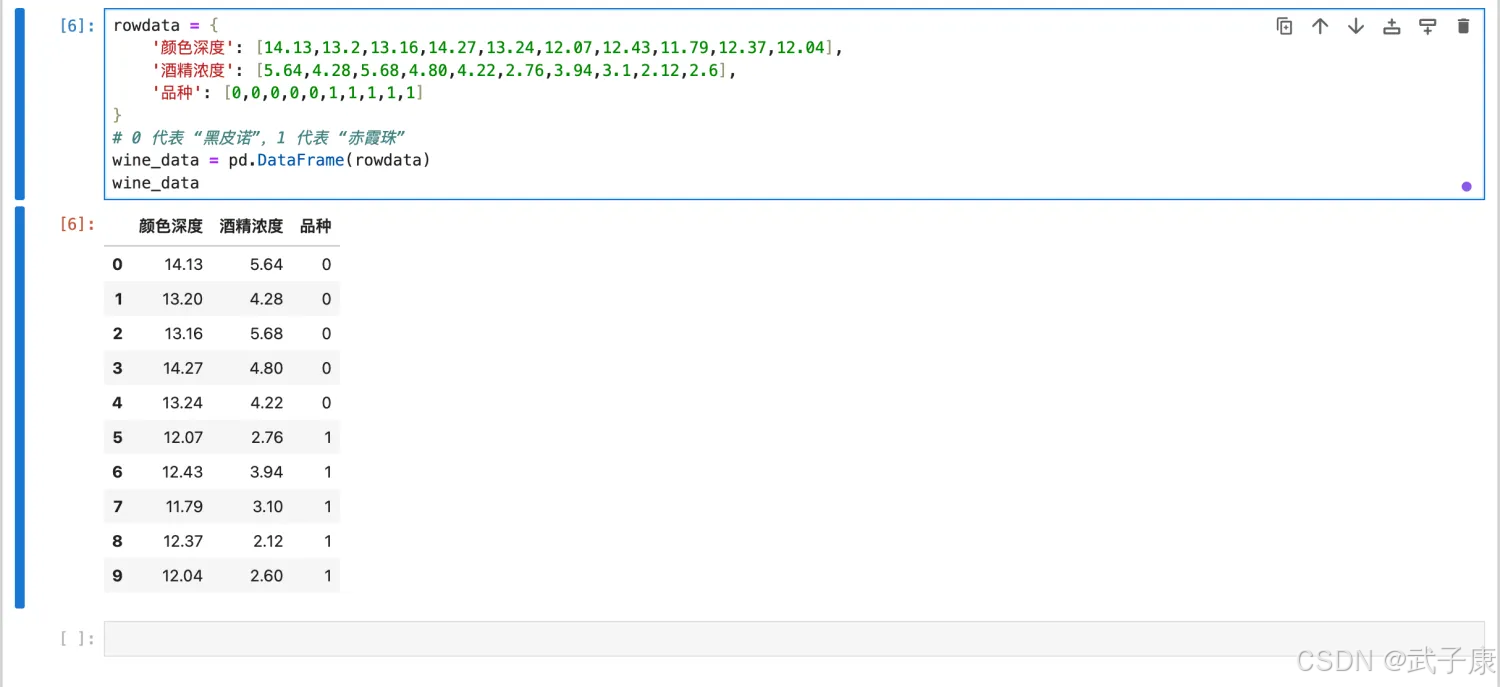
编写代码进行处理:
X = np.array(wine_data.iloc[:,0:2]) #我们把特征(酒的属性)放在Xy = np.array(wine_data.iloc[:,-1]) #把标签(酒的类别)放在Y#探索数据,假如我们给出新数据[12.03,4.1] ,你能猜出这杯红酒是什么类别么?new_data = np.array([12.03,4.1])plt.scatter(X[y==1,0], X[y==1,1], color='red', label='赤霞珠') #画出标签y为1的、关于“赤霞珠”的散点plt.scatter(X[y==0,0], X[y==0,1], color='purple', label='黑皮诺') #画出标签y为0的、关于“黑皮诺”的散点plt.scatter(new_data[0],new_data[1], color='yellow') # 新数据点new_dataplt.xlabel('酒精浓度')plt.ylabel('颜色深度')plt.legend(loc='lower right')plt.savefig('葡萄酒样本.png')执行结果如下如下所示:
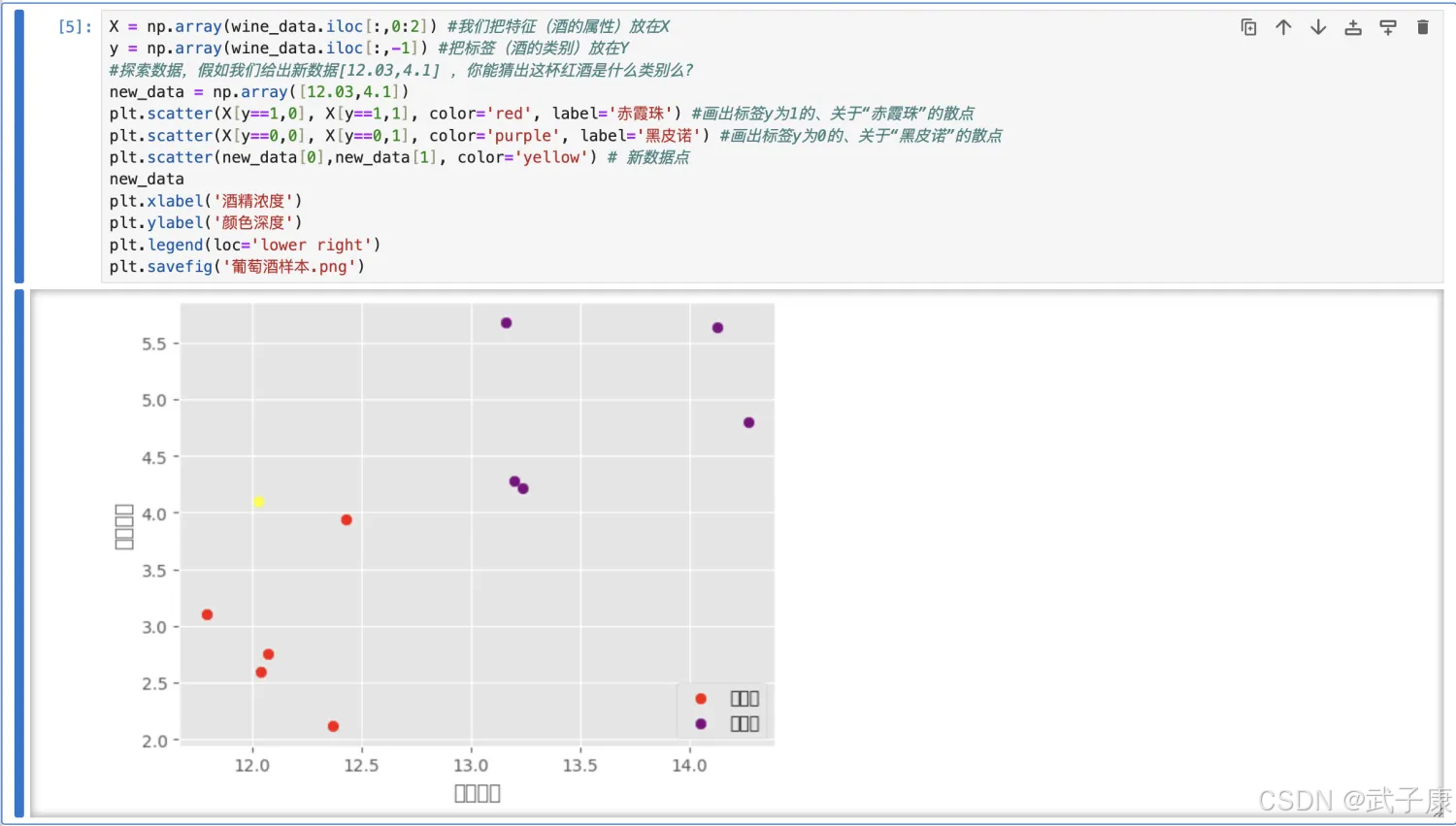
计算已知类别数据集中的点与当前之间的距离
我们使用欧式距离公式,计算新数据点 new_data 与现存的 X 数据集每一个点的距离:
from math import sqrtdistance = [sqrt(np.sum((x-new_data)**2)) for x in X ]distance执行结果如下:
[2.6041505332833594, 1.1837651794169315, 1.9424983912477256, 2.3468276459936295, 1.2159358535712326, 1.3405968819895113, 0.4308131845707605, 1.0283968105745949, 2.0089798406156287, 1.500033332962971]运行结果如下所示:
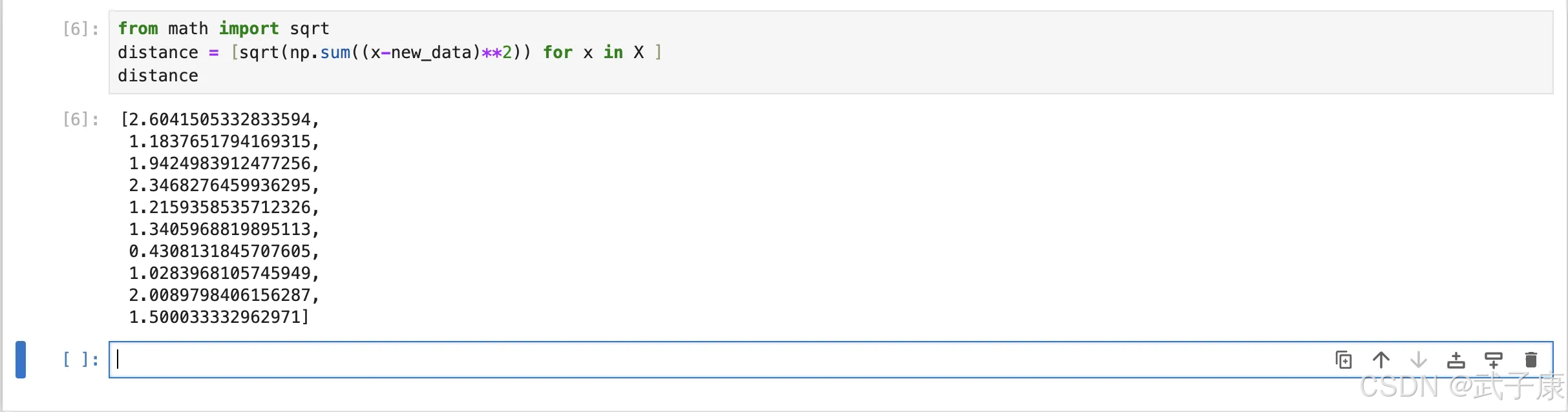
将距离升序排列 选取距离最小的 K 个点
sort_dist = np.argsort(distance)sort_dist执行结果如下所示:

所以,6、7、1 为最近的3个“数据点”的索引值,那么这些索引值对应的原数据的标签是什么?
k = 3topK = [y[i] for i in sort_dist[:k]]topK执行结果如下所示:

确定前k个点所在类别的计数
pd.Series(topK).value_counts().index[0]执行结果如下所示:

封装函数
将数据的过程封装成一个函数:
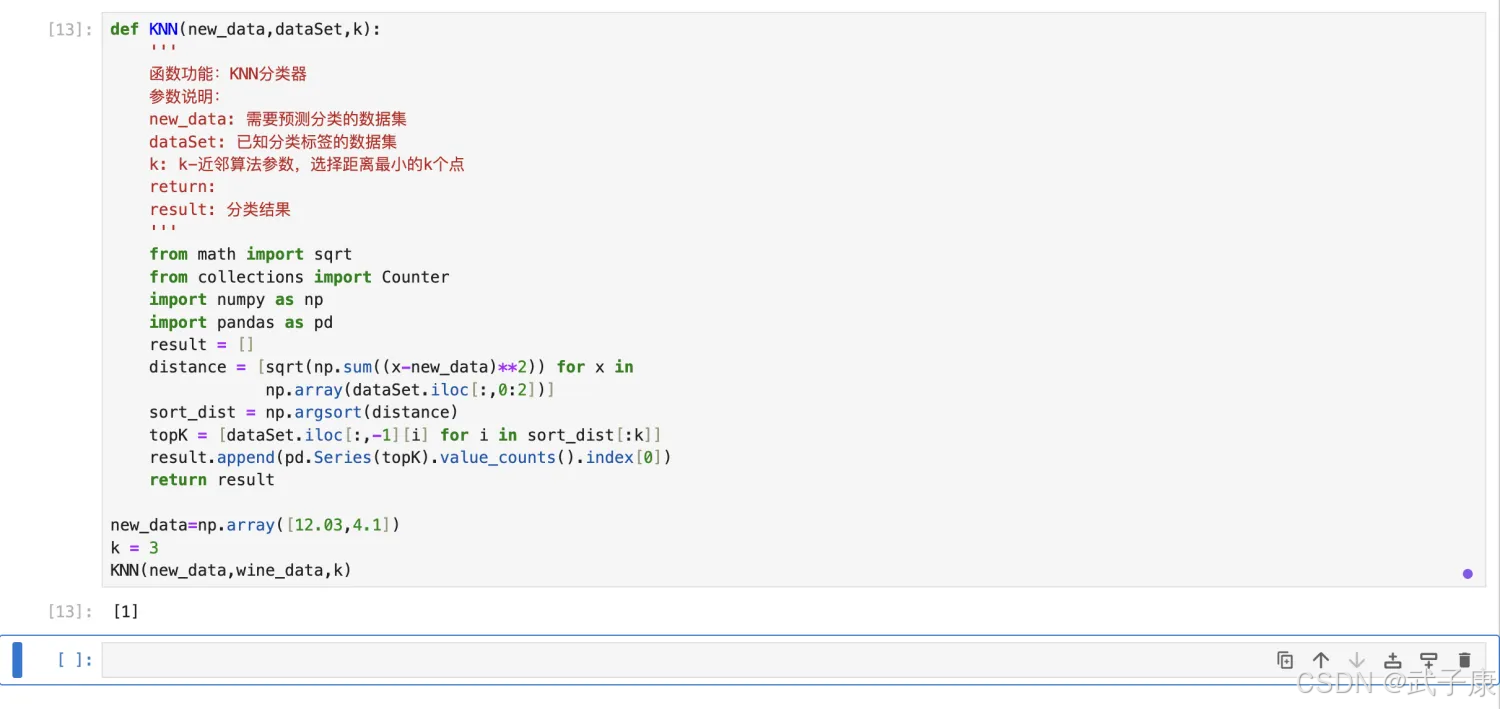
def KNN(new_data,dataSet,k): ''' 函数功能:KNN分类器 参数说明: new_data: 需要预测分类的数据集 dataSet: 已知分类标签的数据集 k: k-近邻算法参数,选择距离最小的k个点 return: result: 分类结果 ''' from math import sqrt from collections import Counter import numpy as np import pandas as pd result = [] distance = [sqrt(np.sum((x-new_data)**2)) for x in np.array(dataSet.iloc[:,0:2])] sort_dist = np.argsort(distance) topK = [dataSet.iloc[:,-1][i] for i in sort_dist[:k]] result.append(pd.Series(topK).value_counts().index[0]) return result测试函数的运行结果:
new_data=np.array([12.03,4.1])k = 3KNN(new_data,wine_data,k)执行结果如下所示: