系列文章目录
用MATLAB形成节点导纳矩阵
文章目录
系列文章目录前言一、程序二、输入原始数据三、所求潮流计算总结
前言
本文通过编写m语言实现牛拉法求潮流计算,所用电力网络图是《用MATLAB形成节点导纳矩阵》中的第一张图。
在这里不讲解牛拉法原理,只贴出代码和相关步骤。
一、程序
n=input('n=');nl=input('nl=');isb=input('isb=');pr=input('pr=');B1=input('B1=');B2=input('B2=');X=input('X=');Y=zeros(n);e=zeros(1,n);f=zeros(1,n);V=zeros(1,n);O=zeros(1,n);S1=zeros(nl);for i=1:n if X(i,2)~=0; p=X(i,1); Y(p,p)=1./X(i,2); endendfor i=1:nl if B1(i,6)==0 p=B1(i,1);q=B1(i,2); else p=B1(i,2);q=B1(i,1); end Y(p,q)=Y(p,q)-1./(B1(i,3)*B1(i,5)); Y(q,p)=Y(p,q); Y(q,q)=Y(q,q)+1./(B1(i,3)*B1(i,5)^2)+B1(i,4)./2; Y(p,p)=Y(p,p)+1./B1(i,3)+B1(i,4)./2;end G=real(Y);B=imag(Y);for i=1:n e(i)=real(B2(i,3)); f(i)=imag(B2(i,3)); V(i)=B2(i,4);endfor i=1:n S(i)=B2(i,1)-B2(i,2); B(i,i)=B(i,i)+B2(i,5);endP=real(S);Q=imag(S);ICT1=0;IT2=1;N0=2*n;N=N0+1;a=0;while IT2~=0 IT2=0;a=a+1; for i=1:n if i~=isb C(i)=0; D(i)=0; for j1=1:n C(i)=C(i)+G(i,j1)*e(j1)-B(i,j1)*f(j1); D(i)=D(i)+G(i,j1)*f(j1)+B(i,j1)*e(j1); end P1=C(i)*e(i)+f(i)*D(i); Q1=f(i)*C(i)-D(i)*e(i); V2=e(i)^2+f(i)^2; if B2(i,6)~=3 DP=P(i)-P1; DQ=Q(i)-Q1; for j1=1:n if j1~=isb&j1~=i X1=-G(i,j1)*e(i)-B(i,j1)*f(i); X2=B(i,j1)*e(i)-G(i,j1)*f(i); X3=X2; X4=-X1; p=2*i-1;q=2*j1-1;J(p,q)=X3;J(p,N)=DQ;m=p+1; J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X4;J(m,q)=X2; elseif j1==i&j1~=isb X1=-C(i)-G(i,i)*e(i)-B(i,i)*f(i); X2=-D(i)+B(i,i)*e(i)-G(i,i)*f(i); X3=D(i)+B(i,i)*e(i)-G(i,i)*f(i); X4=-C(i)+G(i,i)*e(i)+B(i,i)*f(i); p=2*i-1;q=2*j1-1;J(p,q)=X3;J(p,N)=DQ;m=p+1; J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X4;J(m,q)=X2; end end else DP=P(i)-P1; DV=V(i)^2-V2; for j1=1:n if j1~=isb&j1~=i X1=-G(i,j1)*e(i)-B(i,j1)*f(i); X2=B(i,j1)*e(i)-G(i,j1)*f(i); X5=0; X6=0; p=2*i-1;q=2*j1-1;J(p,q)=X5;J(p,N)=DV;m=p+1; J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X6;J(m,q)=X2; elseif j1==i&j1~=isb X1=-C(i)-G(i,i)*e(i)-B(i,i)*f(i); X2=-D(i)+B(i,i)*e(i)-G(i,i)*f(i); X5=-2*e(i); X6=-2*f(i); p=2*i-1;q=2*j1-1;J(p,q)=X5;J(p,N)=DV;m=p+1; J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X6;J(m,q)=X2; end end end endendfor k=3:N0 k1=k+1;N1=N; for k2=k1:N1 J(k,k2)=J(k,k2)./J(k,k); end J(k,k)=1; if k~=3 k4=k-1; for k3=3:k4 for k2=k1:N1 J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2); end J(k3,k)=0; end if k==N0,break;end for k3=k1:N0 for k2=k1:N1 J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2); end J(k3,k)=0; end else for k3=k1:N0 for k2=k1:N1 J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2); end J(k3,k)=0; end endendfor k=3:2:N0-1 L=(k+1)./2; e(L)=e(L)-J(k,N); k1=k+1; f(L)=f(L)-J(k1,N);endfor k=3:N0 DET=abs(J(k,N)); if DET>=pr IT2=IT2+1; endendICT2(a)=IT2;ICT1=ICT1+1;for k=1:n dy(k)=sqrt(e(k)^2+f(k)^2);endfor i=1:n Dy(ICT1,i)=dy(i);endenddisp('迭代次数');disp(ICT1);disp('没有达到精度要求的个数');disp(ICT2);for k=1:n V(k)=sqrt(e(k)^2+f(k)^2); O(k)=atan(f(k)./e(k))*180./pi;endE=e+f*j;disp('各节点的实际电压标幺值E为(节点号从小到大排列):');disp(E);disp('各节点的电压大小V为(节点后从小到大排列):');disp(V);disp('各节点的电压相角O为(节点号从小到大排列):');disp(O);for p=1:n C(p)=0; for q=1:n C(p)=C(p)+conj(Y(p,q))*conj(E(q)); end S(p)=E(p)*C(p);enddisp('各节点的功率S为(节点号从小到大排列):');disp(S);disp('各条支路的首端功率Si为(顺序同您输入B1时一样):');for i=1:nl if B1(i,6)==0 p=B1(i,1);q=B1(i,2); else p=B1(i,2);q=B1(i,1); end Si(p,q)=E(p)*(conj(E(p))*conj(B1(i,4)./2)+(conj(E(p)*B1(i,5))-conj(E(q)))*conj(1./(B1(i,3)*B1(i,5)))); disp(Si(p,q));enddisp('各条支路的末端功率Sj为(顺序同您输入B1时一样):');for i=1:nl if B1(i,6)==0 p=B1(i,1);q=B1(i,2); else p=B1(i,2);q=B1(i,1); end Sj(q,p)=E(q)*(conj(E(q))*conj(B1(i,4)./2)+(conj(E(q)./B1(i,5))-conj(E(p)))*conj(1./(B1(i,3)*B1(i,5)))); disp(Sj(q,p));enddisp('各条支路的功率损耗DS为(顺序同您输入B1时一样):');for i=1:nl if B1(i,6)==0 p=B1(i,1);q=B1(i,2); else p=B1(i,2);q=B1(i,1); end DS(i)=Si(p,q)+Sj(q,p); disp(DS(i));endfor i=1:ICT1 Cs(i)=i;enddisp('这是每次迭代后各节点的电压值(如图所示)');plot(Cs,Dy),xlabel('迭代次数'),ylabel('电压'),title('电压迭代次数曲线');二、输入原始数据
1)节点数n=5;
2)支路数nl=5;
3)支路参数矩阵B1=[1,2,0.03i,0,1.05,0;2,3,0.08i+0.3i,0.5i,1,1;2,4,0.1+0.35i,0,1,1;3,4,0.04+0.25i,0.5i,1,1;3,5,0.015i,0,1.05,1]
它包括六个数据[i,j,z,b,t,it],i,j为支路两端节点号,z为支路的阻抗,b为线路电纳,t为变比,it为高低压侧标志(高为1,低为0)。
4)初始给定值矩阵B2=[0,0,1.05,1.05,0,1;0,3.7+1.3i,1,1.05,0,2;0,2+1i,1,1.05,0,2;0,1.6+0.8i,1,1.05,0,2;5,0,1.05,1.05,0,3]
①节点所接发电机功率SG
②节点负荷功率SL
③节点电压的初始值
④PV节点电压的给定值
⑤节点所接无功补偿设备的容量
⑥节点编号igl
平衡节点为1,PQ节点为2,PV节点为3
5)节点对地阻抗矩阵X=[1,0;2,0;3,0;4,0;5,0](由节点号与接地阻抗构成)。
6)收敛精度 pr=1e-6(一般来说工程上是1e-6到1e-7)

三、所求潮流计算

每次迭代后各节点电压值
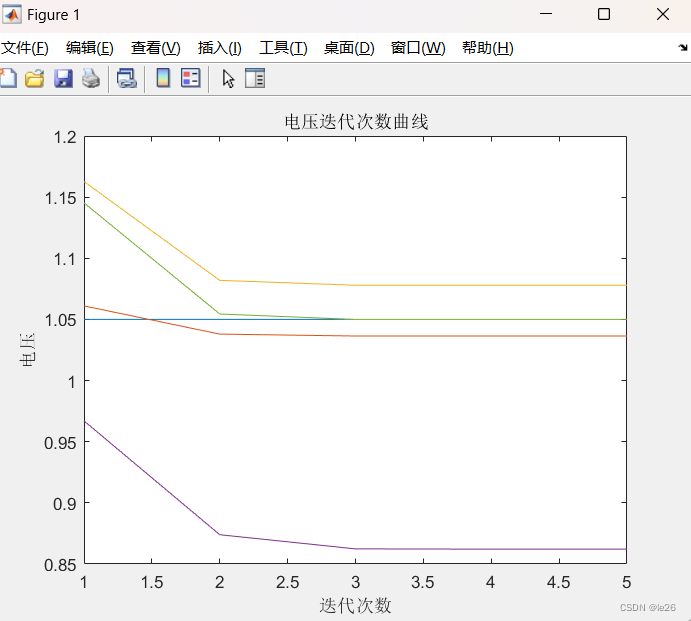
总结
通过不断迭代,牛拉法可以得到电力系统潮流的准确解。它是一种常用且有效的方法,可用于计算电力系统的稳态运行状态。