C语言高精度算法（加、减、乘、阶乘、高除以高，高除以低）

文章目录

前言1. 高精度加法2. 高精度减法3. 高精度乘法高精度×高精度高精度×低精度 + 高精度阶乘 4. 高精度除法高精度除低精度高精度除以高精度 总结

前言

问：为什么会有高精度呢？
答：int表示的范围有限，int 占4个字节，32位，大概能表示10的9次方的数据范围，超过此范围，int型无法表示。
ps：本文知识来源于b站麦克老师讲算法、信息学万老师等，每个会尽量附上例子o(╥﹏╥)o。
目前只写了加法减法乘法，后面等我几天哈哈哈o(╥﹏╥)o

1. 高精度加法

原理
简单来说就是将数拆分，一个一个对应相加，往高位进一，看图

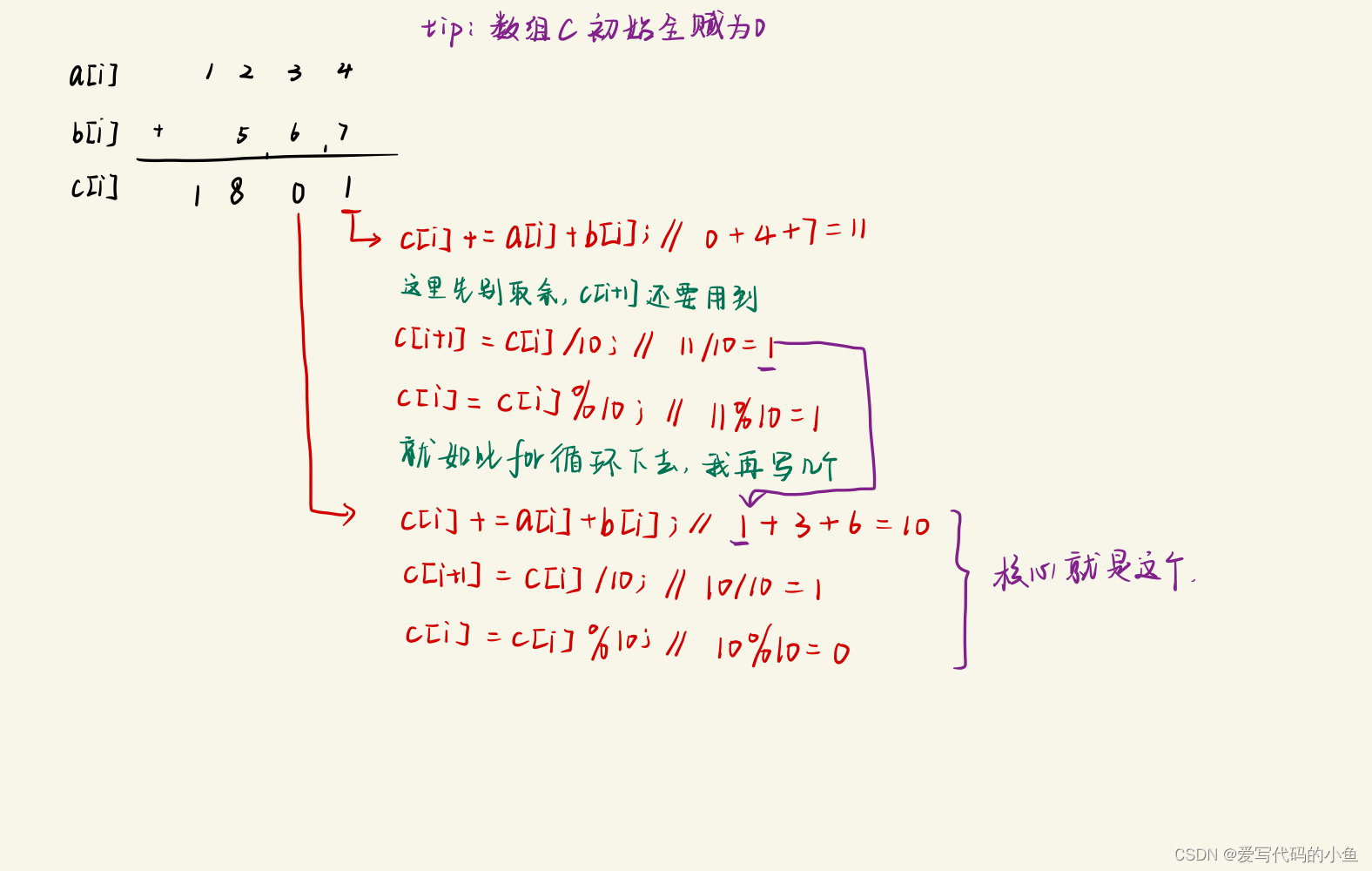
c[i] += a[i] + b[i];c[i+1] = c[i] / 10;c[i] = c[i] % 10;

注意事项
事先定义：数组a，b存的是两个加数，数组c存的是和。
（1） 先定义两个 char 类型的数组存储要输入的元素，再将其转换成 int 类型的进行相加（一开始就定义成 int 类型的无法准确赋值）
原因事例：

#include <stdio.h>#include <string.h>int main () {char s[510];int a[510], len;scanf("%s", s);len = strlen(s);//转换成intfor (int i = 0; i < len; i++) {a[i] = s[i] - '0';}printf("看一下转换后的样子:\n");for (int i = 0; i < len; i++) {printf("%d", a[i]);}printf("\n");//如果不转化，是这样的：printf("如果不转化，是这样的：\n");for (int i = 0; i < len; i++) {a[i] = s[i];printf("%d", a[i]);}}

运行结果：（主要是因为不转换存的是ASCII值）

（2）数组c的长度是数组a、b中长度最大的加1，因为可能会进位，看图

（3）为了方便操作，我们可以将数据反转过来，到时候输出的时候从后往前输出就可以了，注意前导0，看图

（我也试过不翻转直接加，发现太麻烦了，还是翻转省事）
3. 例子（洛谷P1601）

2. 高精度减法

与高精度加法类似，核心还是把数字拆开，一个一个的处理，类比小学减法；

事先说明：定义2个 char 类型的数组 s1,s2，分别存存储减数和被减数；定义2个 int 型的数组 a 和 b ，分别存储将 char 型数字转成 int 型数字，用 int 型数组c存储最终结果；

为了方便操作，可将减数和被减数都逆转，结果逆着输出就可以了；

由于被减数可能比减数小，也是为了方便操作，如果出现这种情况，我们可以将两个操作数互换一下，最后单独输出符号就行了；

与加法一样要处理前导0；

图示：（千言万语尽在图里）

核心代码：

for (int i = 0; i < lenc; i++) {if (a[i] < b[i]){a[i] = a[i] + 10;a[i+1] -= 1;}c[i] = a[i] - b[i];}

（让我偷个懒，没错这个分析就是我的例子里面的分析，O(∩_∩)O哈哈~）
7. 例子在这里

3. 高精度乘法

高精度×高精度

与高精度加法一样啦，还是拆开一个一个对应相乘，在相加，类比小学乘法事先说明：定义两个 char 类型的数组 s1 和 s2，分别存放两个乘数，定义两个 int 型的数组 a 和 b 存放转换后的乘数（将 char 型的 ‘1’ 转成 int 型的 ‘1’），int 型数组c 存放相乘的结果，数组c的长度是数组a与数组b长度之和（这是最长的情况），可以写几个数据试一下：
（这个排版可能在手机上可能有问题，可以用电脑看）

      1 2 3 4   长度为4      |         1 2 3 4     长度为4x       1 1 1   长度为3      |  x          9 9     长度2———————————————              | ————————————————  1 3 6 9 7 4   长度为6      |     1 2 2 1 6 6     长度为6

与加法一样，乘法也要将两个操作数翻转一下，结果也是逆着输出即可，在这里也要处理前导0，处理前导0的代码我改进了一下，在详细说明一下我这个处理前导0的细节（主要是0 * 0 = 0 的情况）

lenc = lenc - 1;if (lenc >= 1) {while (c[lenc] == 0 && lenc >= 1) {lenc--;}}

看一下 0 * 0 = 0 的情况，此时lenc = lena + lenb = 2，数组c的是00即c[0]=0,c[1]=0,所以有lenc = lenc - 1;因为while循环里的判断是c[lenc] == 0在while循环往后，lenc可以当成数组下标来看了，抱歉我写的可能有点绕了

核心代码是这个

for (int i = 0; i < lenb; i++) {for (int j = 0; j < lena; j++) {c[i+j] += b[i] * a[j];c[i+j+1] += c[i+j] / 10;c[i+j] = c[i+j] % 10;}}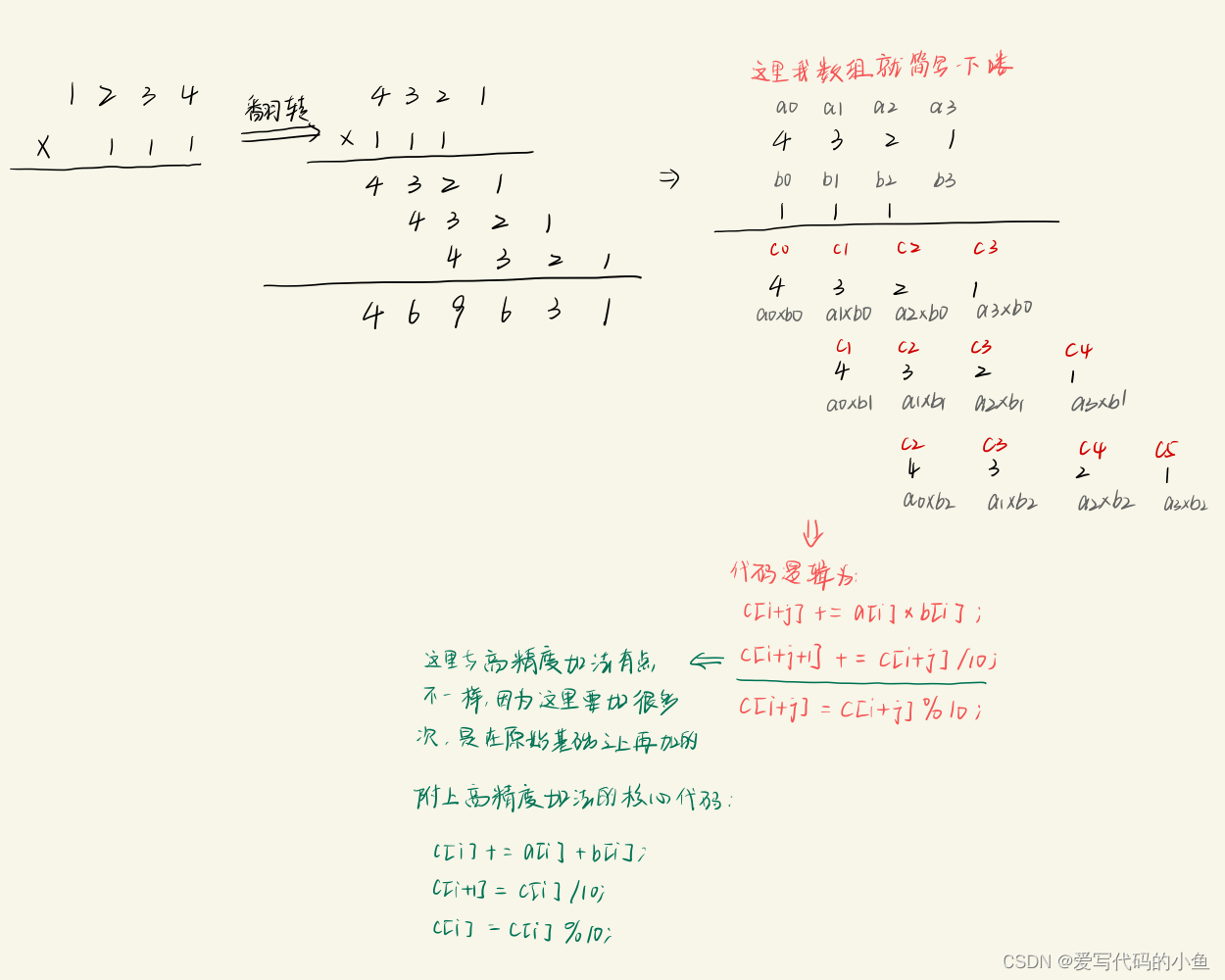

图示理解（千言万语唯有图示能表达出我的想法）
例子（洛谷P1303）

高精度×低精度 + 高精度阶乘

高精度×低精度原理
（1）将高精度的数拆开用数组存储，具体方法为定义 char 类型数组s存储要输入的值，再将其转化成 int 型存入 int 型数组a中，为了方便操作，再将其转置（以上步骤都与我最初写的高精度加法一样）；
（2）低精度看题目要求是用 int 还是 long long；
（3）拆开存入数组a后，逐位与低精度相乘，再进位，此处进位与加法进位不同，最后可能有多位进位，需单独处理；
（4）核心代码：

int jinWei = 0;for (int i = 0; i < lena; i++) {a[i] = a[i]*n + jinWei;jinWei = a[i] / 10;a[i] = a[i] % 10;}//处理进位while (jinWei) {a[lena++] = jinWei % 10;jinWei = jinWei / 10;}

（5）别忘了处理前导0和逆着输出；
（6）图示理解（千言万语尽在图中）：

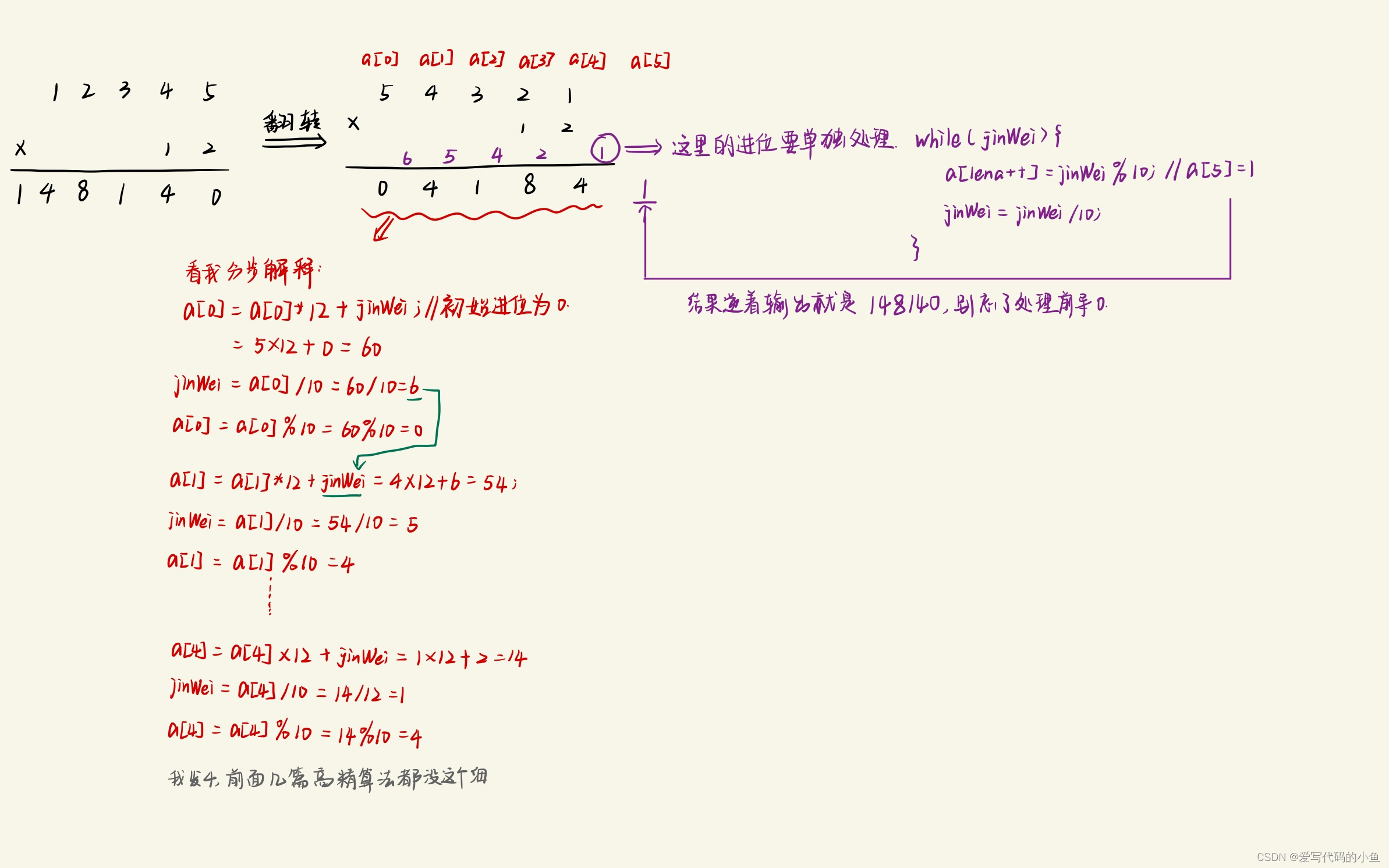
2. 高精度阶乘与高精度×低精度原理很类似，没有太大的区别，就是多乘几次；
3. 那啥，我没找到高精度×低精度的题目，所以下面的代码只是参考，我会贴几个样例，暂时没发现错误，这几个样例运行都是对的哦
完整代码：

#include <stdio.h>#include <string.h>//翻转函数void reverse (int d[510], int len) {int temp, mid = len/2;for (int i = 0, j = len - 1; i < mid, j >= mid; i++, j--) {temp = d[i];d[i] = d[j];d[j] = temp;}}int main () {char s[10000];int a[10000], n;//数组a存的是高精度数，n存的是低精度数scanf("%s%d", s, &n);int lena = strlen(s);for (int i = 0; i < lena; i++) a[i] = s[i] - '0';reverse(a, lena);int jinWei = 0;for (int i = 0; i < lena; i++) {a[i] = a[i]*n + jinWei;jinWei = a[i] / 10;a[i] = a[i] % 10;}//处理进位while (jinWei) {a[lena++] = jinWei % 10;jinWei = jinWei / 10;}//处理前导0lena = lena - 1;while (a[lena] == 0 && lena >= 1){lena--;}//输出for (int i = lena; i>=0; i--) {printf("%d", a[i]);}}

样例1：
输入：123456789 56
运行结果：

样例2：
输入：46572937942 567
运行结果：

4. 高精度阶乘，其实阶乘的核心代码也是上面的那个，只不过阶乘是 1×2×3×…×n，可以当成是高精度数 ×1×2×…×n，把高精度数初值设为1，即a[1] = 1，lena = 1，然后 ×1×2×…×n，×n个低精度的数而已，每次在乘的时候处理进位的同时，lena也会变。
5. 高精度阶乘例子（洛谷[NOIP1998 普及组] 阶乘之和），此例子隐含高精度×低精度。

4. 高精度除法

点击查看例子
两个是共用一个例子的，解析也是直接copy例子上的，可以直接点击例子结合一起看

高精度除低精度

不管是哪种高精度算法，我们都是用数组存储要输入的操作数，这里我不在赘述，相信大家学了其他高精度算法看到这里都明白了，我也不在赘述其他步骤，就讲一下注意事项和思路吧；还记得我们小时候（当然我现在也这样算）怎么算除法吗？列竖式，逐位试商，这里也是差不多的思路，只不过用的是数组模拟；核心代码如下：

//核心代码long long yuShu = 0;//这里注意是long long类型的for (int i = 0; i < lena; i++) {yuShu = yuShu*10 + a[i];c[i] = yuShu / n;yuShu = yuShu % n;}

图解
具体的我也不知道该怎么打字描述，希望我的图可以看懂。

高精度除以高精度

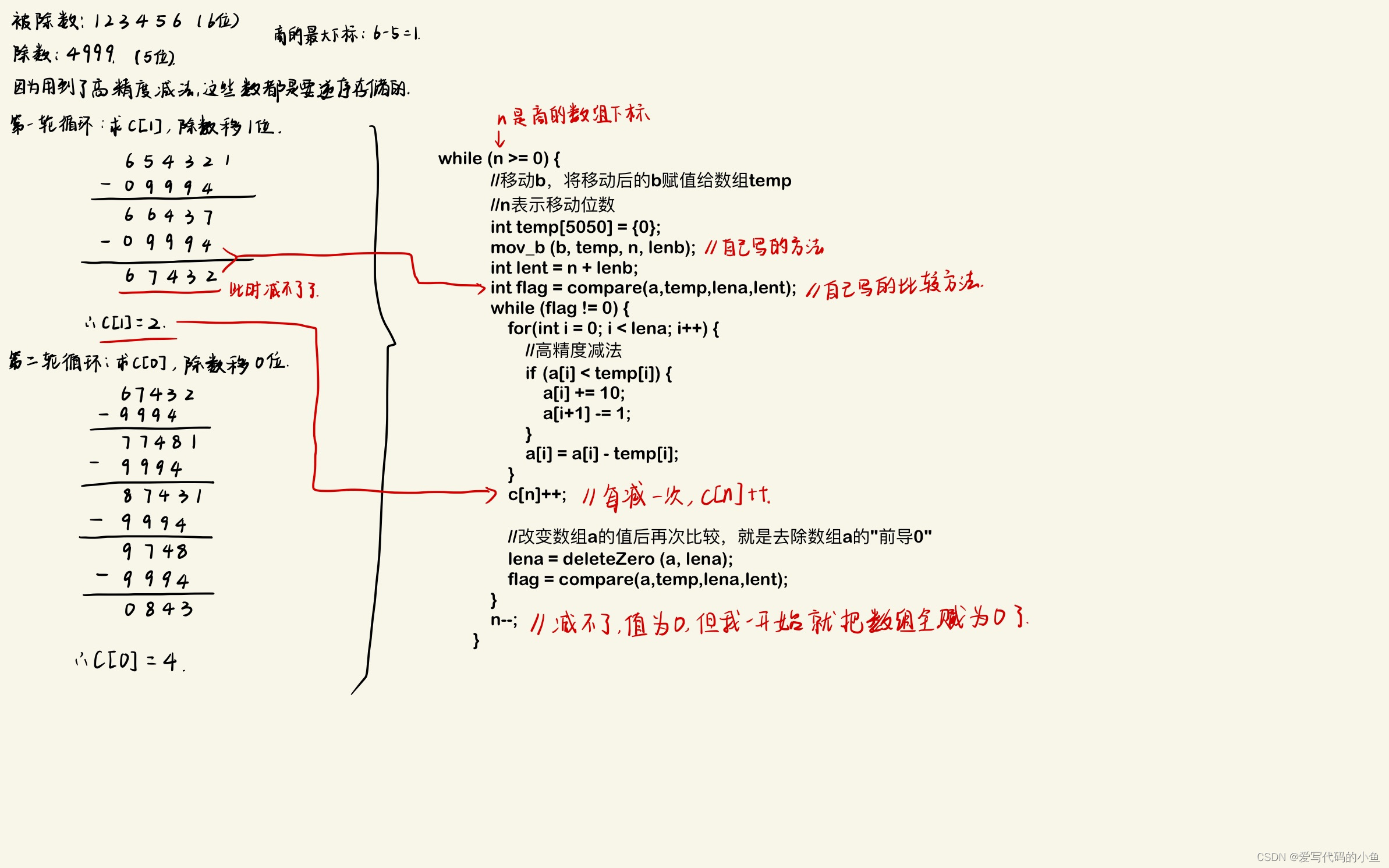
高精度除以高精度就是比较麻烦的了，不是一般的除法，而是通过多次减法来获取最终的值，而且用到了高精度减法，代码比较长，为了看起来简单些，我还写了几个方法封装，代码里都有注释的。核心代码：

while (n >= 0) {//移动b，将移动后的b赋值给数组temp//n表示移动位数int temp[5050] = {0};mov_b (b, temp, n, lenb);int lent = n + lenb;int flag = compare(a,temp,lena,lent);while (flag != 0) {for(int i = 0; i < lena; i++) {//高精度减法if (a[i] < temp[i]) {a[i] += 10;a[i+1] -= 1;}a[i] = a[i] - temp[i];}c[n]++;//改变数组a的值后再次比较，就是去除数组a的"前导0"lena = deleteZero (a, lena);flag = compare(a,temp,lena,lent);}n--;}

看图理解吧

为了更好理解，我带你们写一个例子吧，唔，不要嫌弃我的字哈，感觉得加文字结合才好理解

总结

如若有错，欢迎大家斧正！
高精度算法系列就完结啦~感谢阅读，嘻嘻

2024.1.13