本文介绍了12种常用的距离度量原理、优缺点、应用场景,以及基于Numpy和Scipy的Python实现代码。
笔记工具:Notability
文章目录
- 1. 个人笔记
- 2. 代码实现
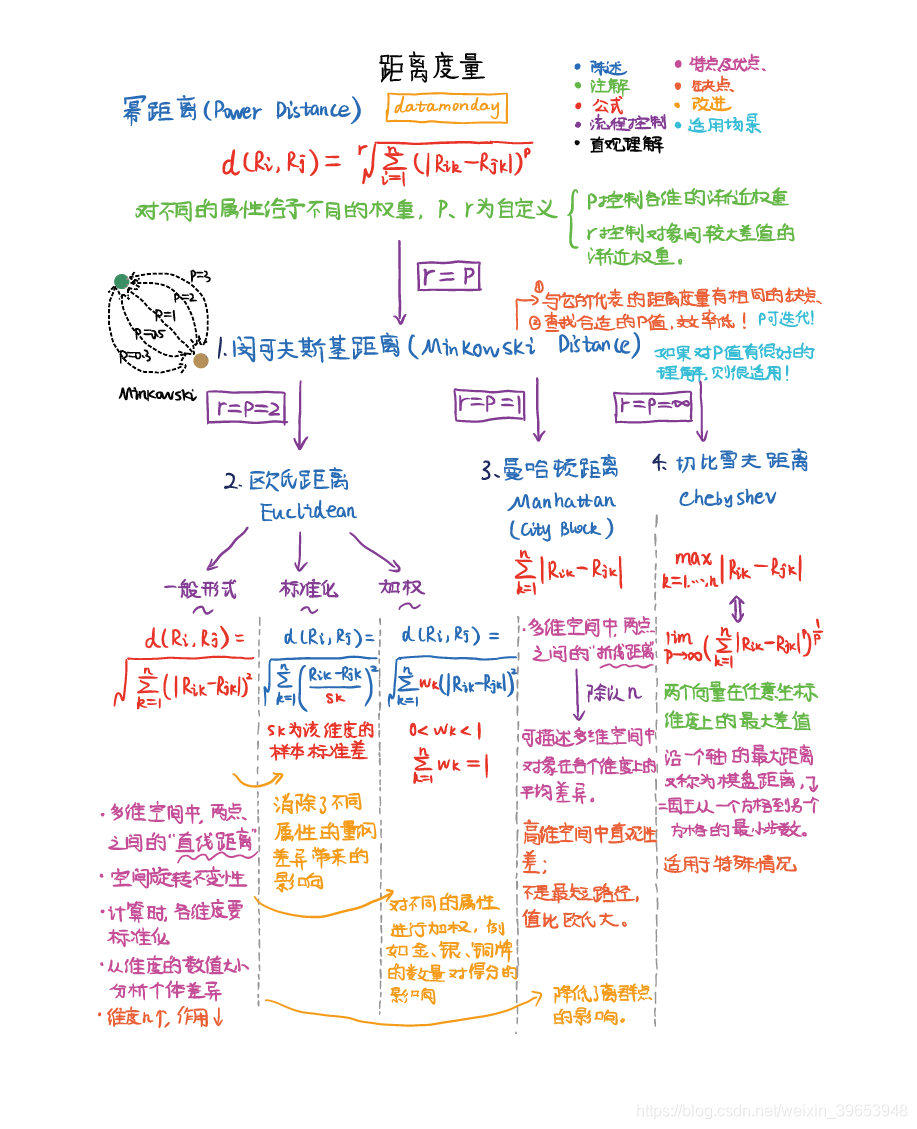
- 1)闵可夫斯基距离(Minkowski Distance)
- 2) 欧氏距离(Euclidean Distance)
- 3) 曼哈顿距离(Manhattan/City Block Distance)
- 4) 切比雪夫距离(Chebyshev Distance)
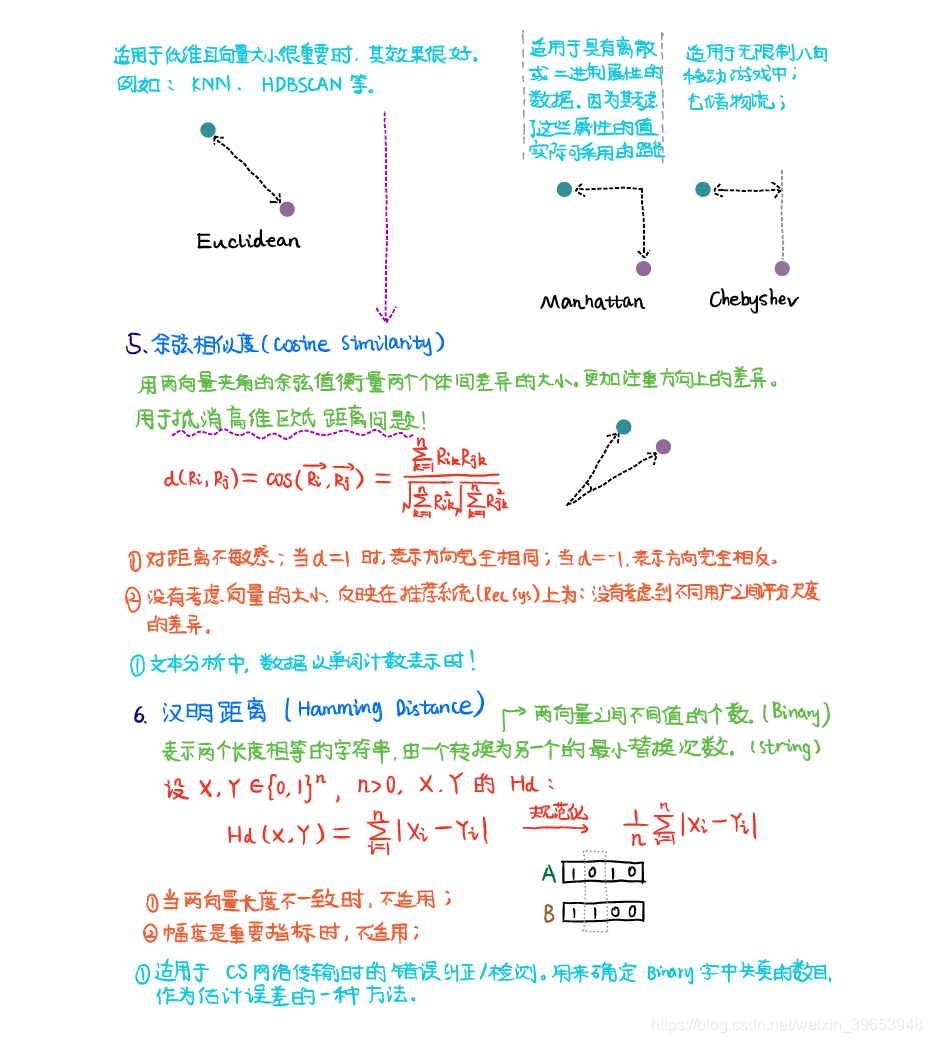
- 5) 余弦相似度(Cosine Similarity)
- 6) 汉明距离(Hamming Distance)
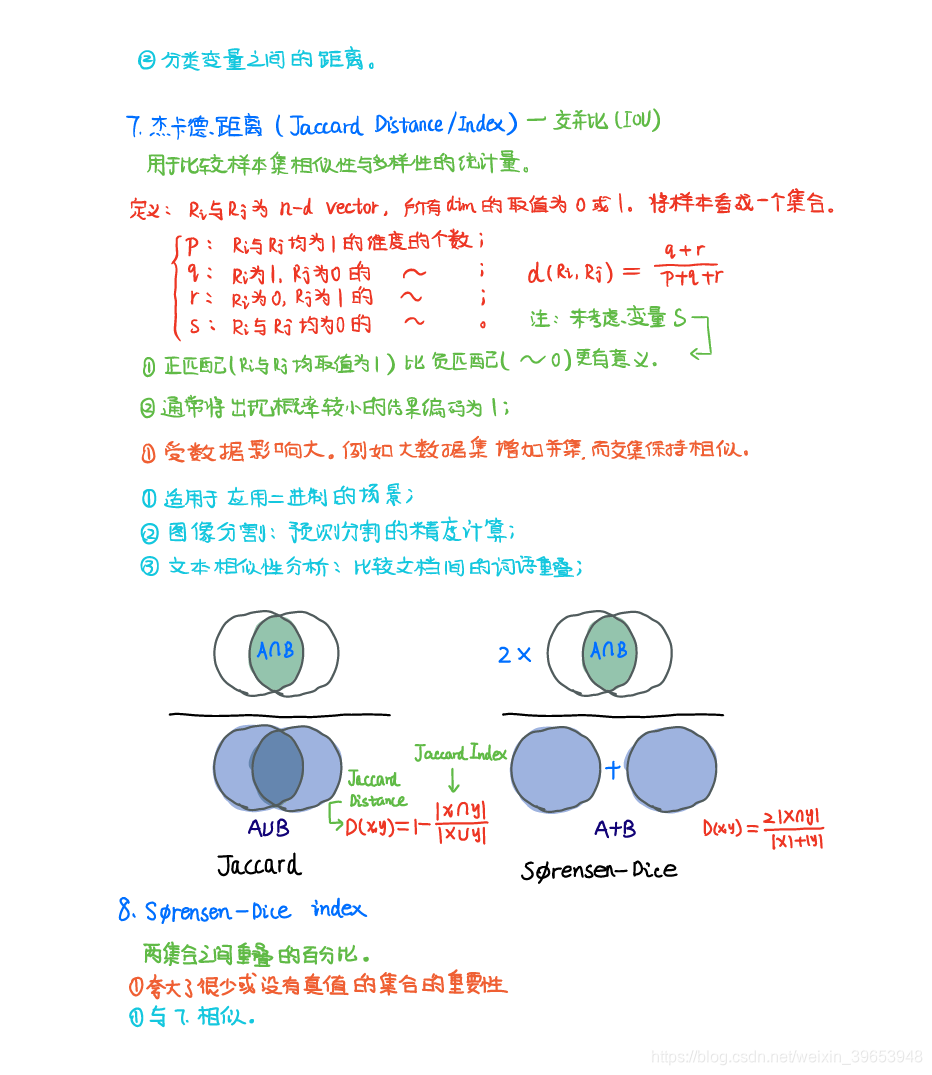
- 7) 杰卡德距离(Jaccard Distance)
- 8) S Φ rensen-Dice
- 9) 半正矢距离(Haversine Distance)
- 10) 斜交空间距离(Oblique Space Distance)
- 11) 兰氏距离(Canberra Distance)
- 12) 马氏距离(Mahalanobis Distance)
1. 个人笔记
笔记工具:Notability
笔记获取:
- 公众号: datazero 回复:DM 获取下载地址。(主页左侧边栏扫码)
- Github:https://github.com/datamonday/BigDataAnalysis


2. 代码实现
导入必要的包,并构造数据。
import numpy as np
from scipy.spatial.distance import pdist
x = np.random.random(5)
# array([0.75173729, 0.34763686, 0.71927609, 0.24151473, 0.22294162])
y = np.random.random(5)
# array([0.98036113, 0.45482745, 0.87472311, 0.92923963, 0.62922737])
1)闵可夫斯基距离(Minkowski Distance)
# p = 2 ——> 欧氏距离
pdist(xy, metric="minkowski", p=2)
2) 欧氏距离(Euclidean Distance)
# 根据公式求解
np.sqrt(np.sum(np.square(x - y) ) )
# 0.8520305805970781
# 根据scipy库求解
xy = np.vstack([x, y])
pdist(xy, metric="euclidean")
# array([0.85203058])
3) 曼哈顿距离(Manhattan/City Block Distance)
np.sum(np.abs(x - y))
# 1.585272101374208
pdist(xy, metric="cityblock")
# array([1.5852721])
4) 切比雪夫距离(Chebyshev Distance)
np.max(np.abs(x - y))
# 0.6877248997688814
pdist(xy, metric="chebyshev")
# array([0.6877249])
5) 余弦相似度(Cosine Similarity)
np.dot(x, y) / ( np.linalg.norm(x) * np.linalg.norm(y) )
# 0.9232011981703329
1 - pdist(xy, metric="cosine")
# array([0.9232012])
6) 汉明距离(Hamming Distance)
np.mean( x != y )
# 1.0
pdist(xy, metric="hamming")
# array([1.])
7) 杰卡德距离(Jaccard Distance)
molecular = np.double( (x != y).sum() )
denominator = np.double(np.bitwise_or( x != 0, y != 0).sum() )
molecular / denominator
# 1.0
pdist(xy, metric="jaccard")
# array([1.])
8) S Φ rensen-Dice
pdist(xy, metric="dice")
# array([0.])
9) 半正矢距离(Haversine Distance)
"""
计算Ezeiza机场(阿根廷布宜诺斯艾利斯)和戴高乐机场(法国巴黎)之间的距离。
"""
from sklearn.metrics.pairwise import haversine_distances
from math import radians
bsas = [-34.83333, -58.5166646]
paris = [49.0083899664, 2.53844117956]
bsas_in_radians = [radians(_) for _ in bsas]
paris_in_radians = [radians(_) for _ in paris]
result = haversine_distances([bsas_in_radians, paris_in_radians])
# multiply by Earth radius to get kilometers
result * 6371000/1000
输出:
array([[ 0. , 11099.54035582],
[11099.54035582, 0. ]])
10) 斜交空间距离(Oblique Space Distance)
11) 兰氏距离(Canberra Distance)
np.sum( np.true_divide( np.abs(x - y), np.abs(x) + np.abs(y) ) )
# 1.4272762731136441
pdist(xy, metric="canberra")
# array([1.42727627])
12) 马氏距离(Mahalanobis Distance)
-
马氏距离要求样本个数>维数,此处重新生成样本集:10个样本,2个属性;
-
马氏距离计算两两样本之间的距离,故结果包含: C 10 2 = 45 C^{2}_{10} = 45 C102=45 个距离分量。
data = np.random.random([10, 2])
data # (10, 2)
array([[0.16057991, 0.03173777],
[0.04984203, 0.63608966],
[0.0965663 , 0.54125706],
[0.14562222, 0.50749436],
[0.12384608, 0.66895134],
[0.38362246, 0.96750912],
[0.66204458, 0.34832719],
[0.62169272, 0.76812896],
[0.55320254, 0.59736334],
[0.53135375, 0.97430267]])
# 求解个维度之间协方差矩阵
S = np.cov(data.T)
# 计算协方差矩阵的逆矩阵
ST = np.linalg.inv(S)
ST
array([[18.39262731, -4.22549979],
[-4.22549979, 13.68987876]])
n = data.shape[0]
d1 = []
for i in range(0, n):
for j in range(i + 1, n):
delta = data[i] - data[j]
d = np.sqrt( np.dot( np.dot(delta, ST), delta.T) )
d1.append(d)
print(len(d1))
d1
45
[2.4064983868149823,
1.9761163000756812,
1.778448926503528,
2.404430793536302,
3.3375019493285927,
2.1576814382238196,
2.9094250412104405,
2.3104822379986585,
3.426008151540264,
0.4480137866843753,
0.7065459737678685,
0.30815685501580464,
1.618002146140689,
3.0847744520164553,
2.3696411013587313,
2.2012364723722557,
2.1104688855720037,
0.2717792884385083,
0.4554926318973598,
1.7230353296945067,
2.7042335514201556,
2.183968292942155,
1.9135693479813816,
2.1102154148029593,
0.6287347650129346,
1.735958615801837,
2.438573435905017,
2.012440681515558,
1.6900976084983395,
2.048918972209157,
1.3438862451280977,
2.862373485815439,
2.067854534269353,
1.928870122984677,
1.8108503250774675,
2.851523901145603,
1.409891022070067,
1.7131869461579778,
0.6273442013634126,
1.608018006961265,
1.1384164544766362,
2.5238527095532692,
0.6218088758251554,
0.94309743685501,
1.422491582300723]
pdist(data, metric="mahalanobis")
array([2.40649839, 1.9761163 , 1.77844893, 2.40443079, 3.33750195,
2.15768144, 2.90942504, 2.31048224, 3.42600815, 0.44801379,
0.70654597, 0.30815686, 1.61800215, 3.08477445, 2.3696411 ,
2.20123647, 2.11046889, 0.27177929, 0.45549263, 1.72303533,
2.70423355, 2.18396829, 1.91356935, 2.11021541, 0.62873477,
1.73595862, 2.43857344, 2.01244068, 1.69009761, 2.04891897,
1.34388625, 2.86237349, 2.06785453, 1.92887012, 1.81085033,
2.8515239 , 1.40989102, 1.71318695, 0.6273442 , 1.60801801,
1.13841645, 2.52385271, 0.62180888, 0.94309744, 1.42249158])
Reference:
- 《大数据分析与挖掘》 ch5:聚类算法
- 数据科学中常见的9种距离度量方法,内含欧氏距离、切比雪夫距离等
- 9 Distance Measures in Data Science