目录
前言什么是最大公约数和最小公倍数最大公约数与最小公倍数的公式求最大公约数方法方法一:暴力穷举法方法二:辗转相除法方法三:更相减损术 求最小公倍数的方法方法一:公式法方法二:暴力穷举法方法三:叠乘法 最后总结
前言
我们在C语言的学习中,经常会遇到这样一些数学题目,良好掌握这些题目有利于我们理解和学习C语言,话不多说,直接进入主题
什么是最大公约数和最小公倍数
最大公约数:
首先我们举个例子,比如12 和16,12的约数有(1,2 ,3,4,6,12),16的约数有(1,2,4,8,16)公约数就是两个数共同的约数,(1,2,4)而公约数中最大的就是最大公约数。
最小公倍数
我们同样举个例子,比如12和16,我们将163=48,124=48,这是两个数第一次有倍数相等关系,就叫48是最小公倍数

最大公约数与最小公倍数的公式
最大公约数 —— Greatest Common Divisor(GCD)
最小公倍数 —— Leatest Common Multiple(LCM)
假设a和b是我们已知的数,那么 就存在一个公式。
公式展示 
a ∗ b = G C D ∗ L C M a*b=GCD*LCM a∗b=GCD∗LCM
这与我们的路程公式很相似,我们可以类比记忆,路程=速度*时间
所以我们只要求出其中的一个就行,求出GCD 就可以通过公式求出LCM,
求出LCM就可以通过公式求出GCD。
求最大公约数方法
方法一:暴力穷举法
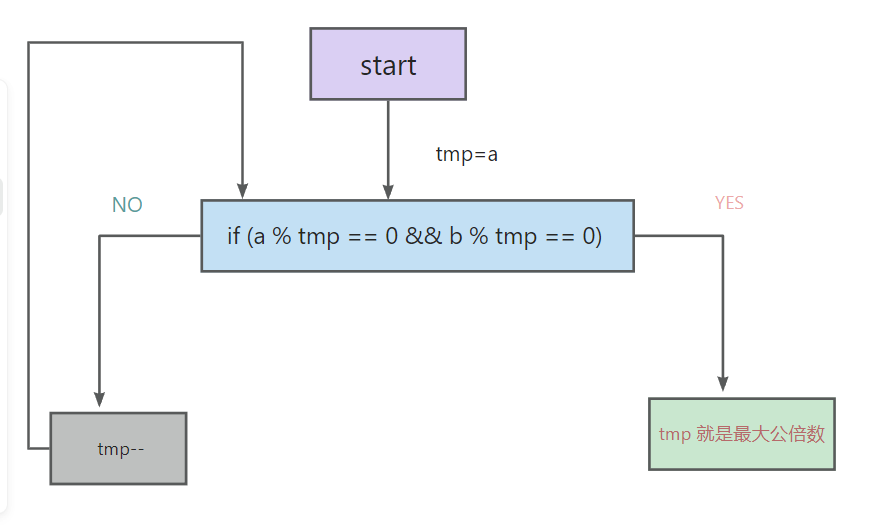
细节讲解: 我们知道最大公约数是约数中能同时整除两数,并且是最先整除的,那我们就可以一个一个试。我们可以将l两个数中小的那个赋给tmp,为什么呢?因为我们找最大公倍数时最大也不会超过a,b两个数中最小的那个。
比如16 和12 ,我们肯定是从12往下找,而不是还要在16~12之间浪费时间。 我们来看看代码
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>int main(){int a = 0;int b = 0;scanf("%d %d", &a, &b);int tmp = a > b ? b : a;while (1){if (a % tmp == 0 && b % tmp == 0){printf("最大公约数是%d", tmp);break;}elsetmp--;}return 0;}

方法二:辗转相除法
在数学中,辗转相除法,又称欧几里得算法(Euclidean algorithm),是求取最大公约数的一种算法。辗转相除法首次出现于欧几里得的《几何原本》中的第Ⅶ卷,书中的命题ⅰ和命题ⅱ所描述的就是辗转相除法,而在中国,辗转相除法最早出现在《九章算法》中。可以说这是一个非常经典的方法
我们来看流程图
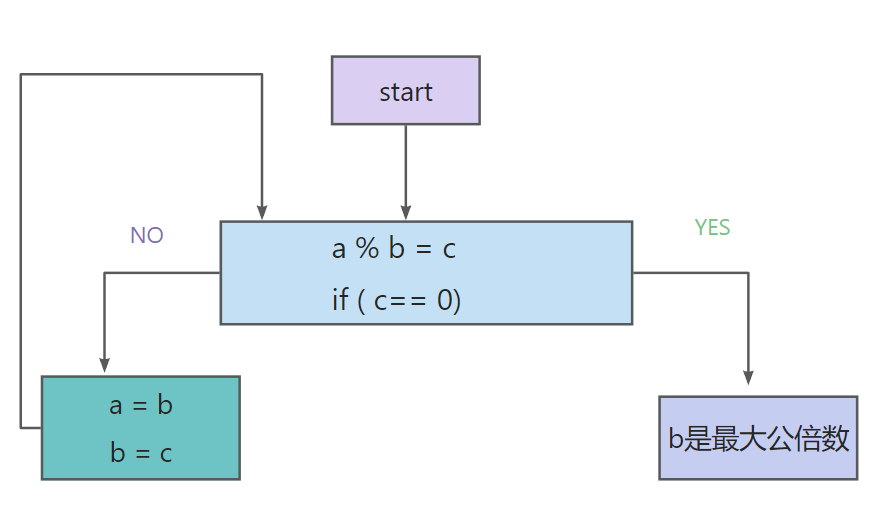
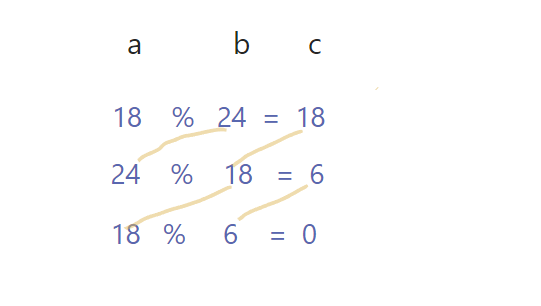
解析:如果我们有a,b a = 24 b = 18 ,我们先让 24 % 18 = 6 ,
接下来我们让 18 % 6 = 0 ;刚好符合我们流程图中蓝色框框的条件,这样就能确定 6 就是最大公倍数。如果是18 % 24 呢?
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>int main(){int a = 0;int b = 0;scanf("%d %d", &a, &b);while (1){int c = a % b;if (0 == a % b){printf("%d就是最大公约数", b);break;}else{a = b ; b = c;}}return 0;}
方法三:更相减损术
《九章算术》是中国古代的数学专著,其中的“更相减损术”可以用来求两个数的最大公约数
流程图:
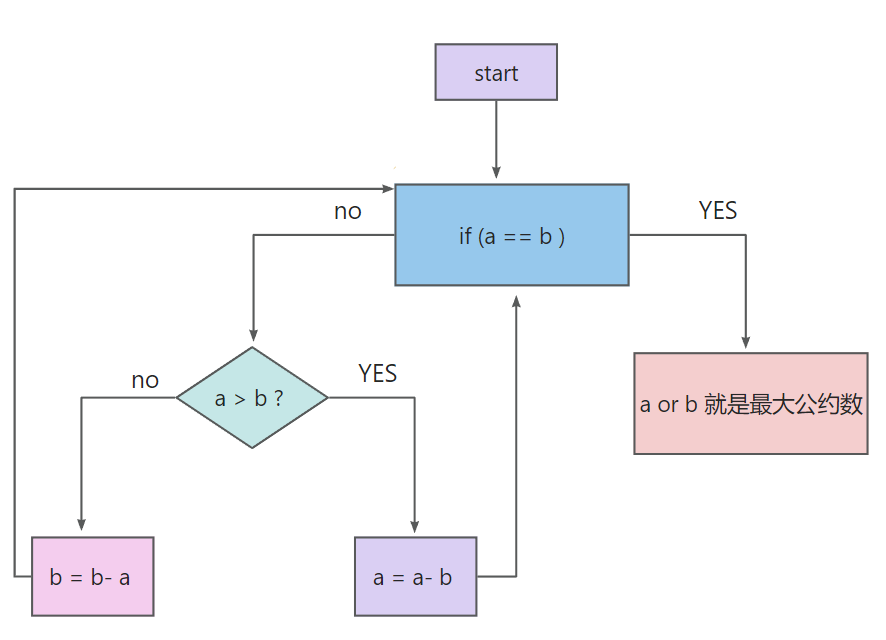
用更相减损术求98与63的最大公约数。

我们只要跟着流程图走,然后一直改变 a 和 b 的值然后直至a b 相等就行,a b 相等时的那个数就是最大公倍数,下面给出代码
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>int main(){int a = 0;int b = 0;scanf("%d %d", &a, &b);while (1){if (a == b){printf("最大公倍数是%d", a);break; }if (a > b){a = a - b;}if (b > a){b = b - a;}}return 0;}
求最小公倍数的方法
方法一:公式法
a ∗ b = G C D ∗ L C M a*b=GCD*LCM a∗b=GCD∗LCM
所以我们只要求出其中的一个就行,求出GCD 就可以通过公式求出LCM,
我们上面已经介绍了三种求GCD的方法,直接用公式也是可以的。
方法二:暴力穷举法
我们知道最小公倍数就是能够同时整除我们已知的两个数的数,而且我们可以从两个数中更大的开始,比如说求45和30的最小公倍数。
我们肯定是从45 往上找。
由于方法比较暴力我们就直接看代码吧!
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>int main(){int a = 0;int b = 0;scanf("%d %d", &a, &b);int c = a > b ? a : b;while (1){if (0 == c % a && 0 == c % b){printf("最小公倍数是%d", c);break;}c++;}return 0;}
方法三:叠乘法
方法讲解:
已知两个数的公倍数一定与这两个数存在倍数关系,那么求解最小公倍数我们就可以将其中一个数依次扩大1倍、2倍、3倍……直到出现第一个扩大n倍的数可以同时整除这两个数,这个数就是最小公倍数。
计算36和270的最小公倍数
我们直接给出代码
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>int main(){int a = 0;int b = 0;scanf("%d %d", &a, &b);int i = 1;while (a * i % b != 0){i++;}printf("最小公倍数是%d", a * i);return 0;}

最后总结
通过这篇博客我们知道了求最大公约数和最小公倍数的许多方法,当然不止这些方法,但是我觉得这些应该够用一段时间了。我是一个博客新手,本文若是有笔误之处,请大家多多指出。最后写博客是一件很辛苦但是很有成就感的一件事情。
这篇文章到这里就结束了,如果有帮到你就请点个赞吧。我的博客是不添加水印的,大家也可以用里面的图片。最后就麻烦用你的小手点个赞吧,哈哈Thanks♪(・ω・)ノ