粒子群优化算法(Particle Swarm Optimization, PSO)是一种基于群体智能的优化算法,由James Kennedy和Russ Eberhart于1995年提出。它模仿鸟群觅食的行为,利用一组“粒子”在搜索空间中进行探索,以寻找最优解。每个粒子代表一个潜在的解,通过与其他粒子的协作和自身的历史经验来更新其位置。
一、基本原理
初始化:
随机生成粒子的位置和速度。初始化每个粒子的个体最佳位置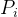 和全局最佳位置
和全局最佳位置 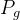 。
。 评估适应度:
计算每个粒子的适应度值(目标函数值)。更新个体最佳和全局最佳:
如果粒子的当前适应度优于个体最佳适应度,则更新个体最佳位置。如果粒子的当前适应度优于全局最佳适应度,则更新全局最佳位置。更新粒子速度和位置:
使用速度更新公式更新每个粒子的速度。使用位置更新公式更新每个粒子的位置。迭代:
重复评估适应度、更新个体最佳和全局最佳、更新速度和位置的步骤,直到达到最大迭代次数或满足停止条件。输出结果:
返回全局最佳位置和适应度作为优化问题的解。二、公式推导
2.1 粒子表示
位置和速度:
每个粒子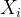 在搜索空间中的位置表示一个可能的解。每个粒子
在搜索空间中的位置表示一个可能的解。每个粒子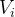 的速度向量决定了其在下一次迭代中的位置更新。
的速度向量决定了其在下一次迭代中的位置更新。 维度:
如果优化问题是 n 维的,则每个粒子的表示也是一个n 维的向量。2.2粒子的状态
个体最佳位置(Personal Best, 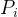 ):
):
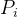 。该位置是粒子在历史迭代中所找到的最优解。
。该位置是粒子在历史迭代中所找到的最优解。 全局最佳位置(Global Best, 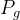 ):
):
2.3更新规则
粒子的位置和速度通过以下公式进行更新:
速度更新公式:
![]()
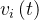 是粒子 i在第 t代的速度。
是粒子 i在第 t代的速度。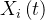 是粒子 i 在第 t代的位置。
是粒子 i 在第 t代的位置。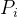 是粒子 i的个体最佳位置。
是粒子 i的个体最佳位置。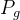 是全局最佳位置。w 是惯性权重,用于控制粒子当前速度的影响。
是全局最佳位置。w 是惯性权重,用于控制粒子当前速度的影响。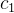 和
和 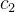 是学习因子,用于控制粒子向个体最佳位置和全局最佳位置靠近的程度。
是学习因子,用于控制粒子向个体最佳位置和全局最佳位置靠近的程度。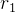 和
和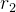 是在 [0,1] 范围内的随机数,用于引入随机性。
是在 [0,1] 范围内的随机数,用于引入随机性。 位置更新公式:
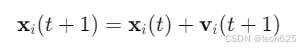
粒子的位置通过加上更新后的速度来更新。
2.4参数设置
惯性权重 w:
控制粒子速度的影响。较大的惯性权重有助于全局搜索,较小的惯性权重有助于局部搜索。学习因子 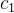 和
和 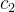 :
:
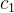 和
和 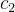 的值在 1 到 2 之间。
的值在 1 到 2 之间。 随机数 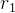 和
和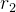 :
:
三、MATLAB仿真
下面是一个基于MATLAB的粒子群优化算法示例程序,用于寻找一个简单的优化问题的最优解。例如,优化目标函数 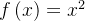 的最小值。
的最小值。
% 粒子群优化算法参数设置nParticles = 30; % 粒子数量nDimensions = 1; % 变量维度nIterations = 100; % 迭代次数w = 0.5; % 惯性权重c1 = 1.5; % 个体学习因子c2 = 1.5; % 全局学习因子% 初始化粒子位置和速度positions = rand(nParticles, nDimensions) * 10 - 5; % 在 [-5, 5] 范围内初始化velocities = rand(nParticles, nDimensions) * 2 - 1; % 在 [-1, 1] 范围内初始化personalBestPositions = positions; % 个人最佳位置初始化为当前位置personalBestScores = arrayfun(@(i) objectiveFunction(positions(i, :)), 1:nParticles); % 个人最佳适应度[globalBestScore, bestIndex] = min(personalBestScores); % 全局最佳适应度globalBestPosition = personalBestPositions(bestIndex, :); % 全局最佳位置% 主循环:迭代粒子群优化for iter = 1:nIterations % 计算适应度 scores = arrayfun(@(i) objectiveFunction(positions(i, :)), 1:nParticles); % 更新个体最佳 betterMask = scores < personalBestScores; personalBestPositions(betterMask, :) = positions(betterMask, :); personalBestScores(betterMask) = scores(betterMask); % 更新全局最佳 [currentBestScore, bestIndex] = min(personalBestScores); if currentBestScore < globalBestScore globalBestScore = currentBestScore; globalBestPosition = personalBestPositions(bestIndex, :); end % 更新速度和位置 r1 = rand(nParticles, nDimensions); r2 = rand(nParticles, nDimensions); velocities = w * velocities ... + c1 * r1 .* (personalBestPositions - positions) ... + c2 * r2 .* (globalBestPosition - positions); positions = positions + velocities; % 显示当前迭代的全局最佳解 disp(['Iteration: ', num2str(iter), ', Best Position: ', num2str(globalBestPosition), ', Best Score: ', num2str(globalBestScore)]);end% 目标函数(优化目标)function score = objectiveFunction(x) score = x.^2; % 目标是最小化 x^2end代码解释
参数设置:
nParticles:粒子数量。nDimensions:优化问题的维度(在此示例中为1维)。nIterations:迭代次数。w:惯性权重。c1 和 c2:个体学习因子和全局学习因子。 初始化:
粒子的位置和速度被随机初始化。个人最佳位置和适应度被初始化为当前的位置和适应度。全局最佳位置和适应度从个人最佳中选择。主循环:
计算所有粒子的适应度。更新每个粒子的个体最佳位置和适应度。更新全局最佳位置和适应度。根据更新规则调整粒子的速度和位置。目标函数:
在此示例中,目标函数是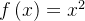 ,目标是找到 x 的最小值。
,目标是找到 x 的最小值。 四、总结
粒子群优化算法是一种简单而有效的优化算法,具有良好的全局搜索能力。通过调整惯性权重和学习因子,可以在不同的问题上进行优化。此MATLAB示例提供了PSO算法的基本实现,并可以根据需要扩展到多维问题和更复杂的目标函数。
优化算法算法以往链接:
优化算法(一)—遗传算法(Genetic Algorithm)附MATLAB程序-CSDN博客