今天做数据结构题,发现了一道很有趣的题目,该题目具体如下:
【问题描述】输入整数N( 1 <= N <= 10 ),生成从1~N所有整数的全排列。
【输入形式】输入整数N。
【输出形式】输出有N!行,每行都是从1~N所有整数的一个全排列,各整数之间以空格分隔。各行上的全排列不重复。输出各行遵循“小数优先”原则, 在各全排列中,较小的数尽量靠前输出。如果将每行上的输出看成一个数字,则所有输出构成升序数列。具体格式见输出样例。
【样例输入1】1
【样例输出1】1
【样例说明1】输入整数N=1,其全排列只有一种。
【样例输入2】3
【样例输出2】
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
【样例说明2】输入整数N=3,要求整数1、2、3的所有全排列, 共有N!=6行。且先输出1开头的所有排列数,再输出2开头的所有排列数,最后输出3开头的所有排列数。在以1开头的所有全排列中同样遵循此原则。
【样例输入3】10
【样例输出3】
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 10 9
1 2 3 4 5 6 7 9 8 10
1 2 3 4 5 6 7 9 10 8
1 2 3 4 5 6 7 10 8 9
1 2 3 4 5 6 7 10 9 8
1 2 3 4 5 6 8 7 9 10
1 2 3 4 5 6 8 7 10 9
1 2 3 4 5 6 8 9 7 10
1 2 3 4 5 6 8 9 10 7
……………………
【样例说明3】输入整数N=10,要求整数1、2、3、……、10的所有全排列。上例显示了输出的前10行。
【运行时限】要求每次运行时间限制在20秒之内。超出该时间则认为程序错误。提示:当N增大时,运行时间将急剧增加。在编程时要注意尽量优化算法,提高运行效率。
【评分标准】该题要求输出若干行整数。
然后答案代码如下:
#include <stdio.h>#include <stdlib.h>void generatePermutations(int arr[], int N);void printPermutation(int arr[], int N);int compare(const void *a, const void *b);int next_permutation(int arr[], int N);int main() { int N; scanf("%d", &N); int arr[N], i; for (i = 0; i < N; i++) { arr[i] = i + 1; } generatePermutations(arr, N); return 0;}void generatePermutations(int arr[], int N) { int i; qsort(arr, N, sizeof(int), compare); // 对数组进行排序,确保从小到大排列 do { printPermutation(arr, N); // 输出排列 } while (next_permutation(arr, N)); // 获取下一个排列}void printPermutation(int arr[], int N) { int i; for (i = 0; i < N; i++) { printf("%d ", arr[i]); } printf("\n");}int compare(const void *a, const void *b) { return (*(int *)a - *(int *)b);}int next_permutation(int arr[], int N) { int i = N - 2; while (i >= 0 && arr[i] >= arr[i + 1]) { i--; } if (i < 0) { return 0; // 已经是最后一个排列,无法获取下一个排列 } int j = N - 1; while (arr[j] <= arr[i]) { j--; } int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; int left = i + 1, right = N - 1; while (left < right) { temp = arr[left]; arr[left] = arr[right]; arr[right] = temp; left++; right--; } return 1;}刚开始看到这个代码,我实在是一脸的疑惑------这是递归了个啥啊!等到上网搜索了好久,我才搞明白这个这个典型问题--全排列问题。
关于解决这个问题的方法,其实无外乎还是运用了回溯算法。
以下是我提炼出来的相关代码:
#include <stdio.h>int mark[11],a[11];void dfs(int step,int n);int main(){int n=0;scanf("%d",&n);dfs(1,n);return 0;} void dfs(int step,int n){if(step>n){int i=0;for(i=1;i<=n;i++){printf("%d",a[i]);if(i!=n){printf(" ");}else printf("\n");}}else{int i=0; for(int i=1;i<=n;i++){if(mark[i]==0){mark[i]=1;a[step]=i;dfs(step+1,n);mark[i]=0;}}}}下面我以n=3为例画了一张图标,可能可以看的更清楚些。
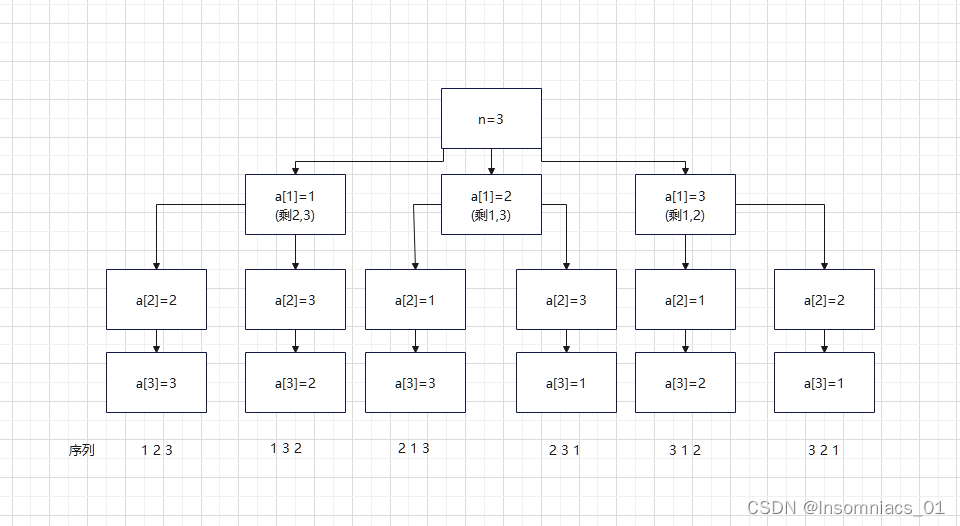
很典型的多叉树对不对。
现在,对dfs函数进行一下详解:
首先在主函数中传入
dfs(1,n);表示step=1,即执行第一步(数组中一共有step-1个元素),而上限为n,表示一共执行n步(即数组一共有n个元素)。
当进入dfs函数后
if(step>n){int i=0;for(i=1;i<=n;i++){printf("%d",a[i]);if(i!=n){printf(" ");}else printf("\n");}}先判断step是否比n大,当step>n时,表示数组中此时的元素个数>=n(当然不可能>n,因为在等于n时就停止了)。此时打印数组。
当step<=n,现在数组还没有填满
else{int i=0; for(i=1;i<=n;i++){if(mark[i]==0){mark[i]=1;a[step]=i;dfs(step+1,n);mark[i]=0;}}}还记得我们在我们定义的全局变量a[11],mark[11]吗?
int mark[100],a[10];由于定义的是全局变量,所以系统自动默认将a与mark的内容全部置为0。
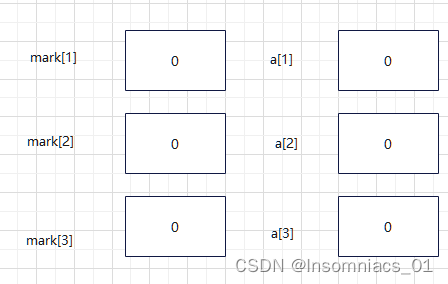
现在进入for循环,当i=1时mark[i]==0
我们将a[1]置为1,同时将mark[1]也置为1,表示第一个位置已经被访问。
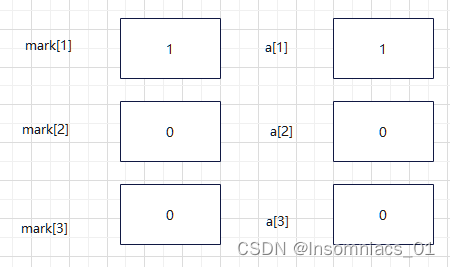
然后进入dsf(2,3) (假设n=3)
进来之后,由于现在step=2,n=3即step<=n,所以进入else语句中
for循环还是从1开始,不过,在上一步中,我们已经将mark[1]置为1,这就不再符合mark[i]==0的条件,所以现在i来到2
由于mark的内容全部置为0,而上一步中只是将mark[1]置为1,mark[2],mark[3]依旧等于0
在i=2时,进入if判断,我们将a[2]置为2,同时将mark[2]置为1
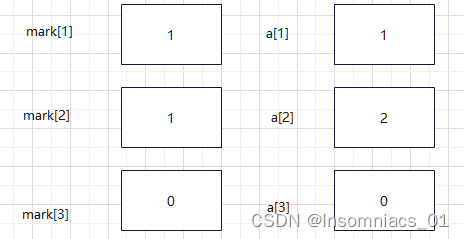
然后进入dfs(3,3)递归中
当step=3时,依旧没有>n,所以还是没有进入打印阶段,进入了else语句
在for循环中,当i=1,2时,mark[i]都是等于1,if判断不成立,但当i=3时,mark[3]=0,进入了if语句
在if语句中,先将mark[3]内容置为1,同时将a[3]置为3
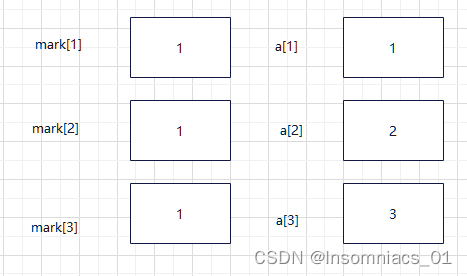
然后执行递归dfs(4,3)
在这次递归中,step=4,n=3,step>n,所以将a中的内容进行了输出打印,
打印输出1 2 3\n
而没有进入else语句,也就没有进入下一个递归中,本次递归结束
dfs(4,3)执行完成
dfs(4,3)是在step=3,i=3时执行进行的,执行结束后,执行语句
mark[i]=0;i=3
所以将mark[3]置为0;

然后i++将i变成了4,不再符合i<=n的条件,跳出for循环,也跳出了else语句,不再进行下一次递归
现在dfs(3,3)执行完毕
回到dfs(2,3)中
将mark[2]置为0,i++

现在i=3
由于在dfs(3,3)的最后,我们已经将mark[3]置为0,所以i=3时,进入if语句
将mark[3]置为1,a[2]置为3
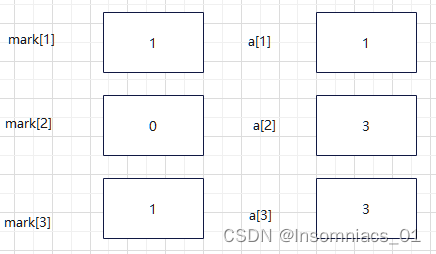
进入dfs(3,3)中
现在还是dfs(3,3),但不同的是,现在a[2]=3 (之前a[2]=2) mark[3]=1,mark[2]=0(之前mark[2]=1,mark[3]=0)
在if语句中,mark[1],mark[3]都等于1
当i=2时进入if语句
将mark[2]置为1,a[3]置为2
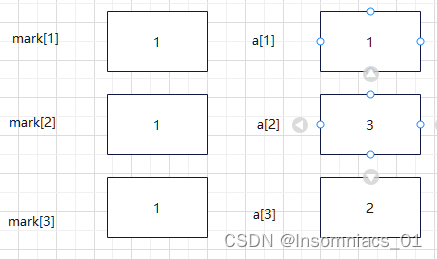
进入dfs(4,3)
现在打印输出a数组----1 3 2(递归结束),返回上一步dfs(3,3)i=2
将mark[2]置为0,同时i++
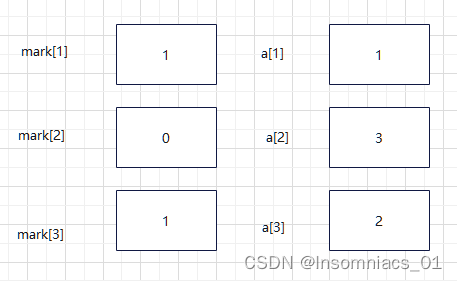
i=3时不符合,i++
i=4时跳出for循环
返回语句dfs(2,3)i=3
将mark[3]置为0
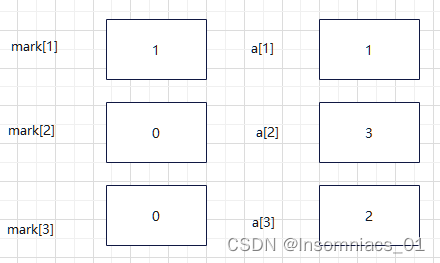
i++,i=4
跳出循环,dfs(2,3)执行完毕
回到dfs(1,3)此时i=1,将mark[1]置为0
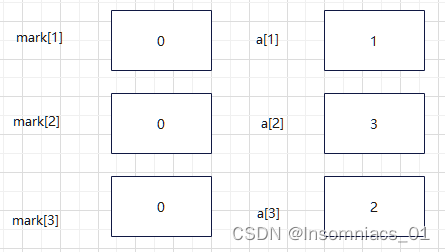
i++,i=2,进入if语句
mark[2]=1,a[1]=2
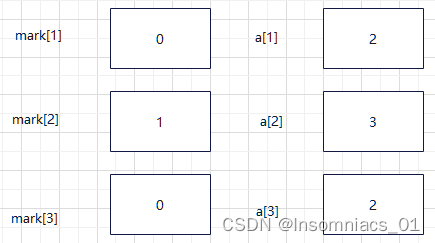
进入dfs(2,3)
后续情况与前面相同,有兴趣可以继续推演
这里建议一下在写代码的时候可以画图辅助一下,很多时候想不明白的问题画一画图就有思路了,抓住这个思路来写代码,可以事半功倍
希望大家可以很好的理解全排列算法!