1. 整数在内存中的存储
计算机中的整数有三种2进制表示方法 :原码、反码、补码。
三种表示方式均有符号位和数值位两个部分,最高一位的是符号位,剩下的都是数值位。符号位用“0”表示“正”,用“1”表示“负”。
正数的原、反、补码都相同。而负整数的三种表示方法各不相同,说明如下:
原码:符号位为“1”,数值位按数值的二进制形式表示
反码:符号位不变,数值位依次按位取反
补码:反码 + 1
对于整形来说,内存中存储的是补码。
为什么呢?
在计算机系统中,数值统一用补码来表示和存储。使用补码,可以将符号位和数值位统一处理;同时,可以将加法和减法统一处理(CPU只需要一个加法器)。补码和原码之间的转换相对简单,不需要复杂的额外硬件电路,这进一步简化了硬件设计。
2. 大小端字节序
2.1 大小端介绍
当存储的数据超过一个字节的时候,就会出现存储顺序的问题,存储顺序分为大端字节序存储和小端字节序存储。说明如下:
大端字节序存储:数据的低位字节内容保存在内存的高地址处,而数据的高位字节内容保存在内存的低地址处小端字节序存储:数据的低位字节内容保存在内存的低地址处,而数据的高位字节内容保存在内存的高地址处为什么会有大小端模式之分呢?
在计算机系统中,每个地址单元都对应着一个字节(byte),一个字节为8bit位,但是在C语言中除了8bit的char以外,还有32bit的int,那对于位数大于8位的处理器,例如32位处理器,由于寄存器宽度大于一个字节,那么必然存在一个字节顺序安排的问题,此时,大端和小端模式应用而生。
2.2 经典练习题
练习1:判断当前机器的字节序
#include<stdio.h>int check_sys(){int i = 1;return (*(char*)&i);}int main(){int ret = check_sys();if(return == 1){printf("Xiao");}else{printf("Da");}return 0;}//check_sys2int check_sys(){union{int i;int c;}un.i = 1;return un.c;}练习2:
#include<stdio.h>int main(){char a = -1;signed char b = -1;unsigned char c = -1;printf("%d\n%d\n%d\n",a,b,c);return 0;}练习3:
#include<stdio.h>int main(){char a = -128;printf("%d\n",a);a = 128;printf("%d\n",a);return 0;}练习4:
#include<stdio.h>int main(){char a[1000];int i;for(i = 0;i < 1000; i++){a[i]= -1 - i;}printf("%d",strlen(a));return 0;}练习5:
#include<stdio.h>unsigned char i = 0;int main(){for(i = 0;i <= 255;i++){printf("hello world\n");}return 0;}#include<stdio.h>int main(){unsigned int i;for(i = 9; i >= 0;i--){printf("%u\n",i);}return 0;}练习6:
#include<stdio.h>int main(){int a[4] = { 1, 2, 3, 4 };int *ptr1 = (int *)(&a + 1);int *ptr2 = (int *)((int)a + 1);printf("%x,%x",ptr1[-1], *ptr2);return 0;}运行 练习2~6 的代码,思考数据在内存中存储的小细节。
3. 浮点数在内存中的存储
根据国际标准IEEE(电气和电子工程协会)754,任意一个二进制浮点数V可以表示成下面的形式:

例如:
十进制的5.0,写成二进制是101.0,等同于1.01 × 2^2。
按照上方V的格式,可以得出S=0,M=1.01,E=2。
十进制的-5.0,等同于-1.01 × 2^2。
按照上方V的格式,可以得出S=1,M=1.01,E=2。
IEEE754规定:
对于32位的浮点数,最高的1位存储符号位S,接着的8位存储指数E,剩下的23位存储有效数字M。

对于64位的浮点数,最高的1位存储符号位S,接着的11位存储指数E,剩下的52位存储有效数字M。
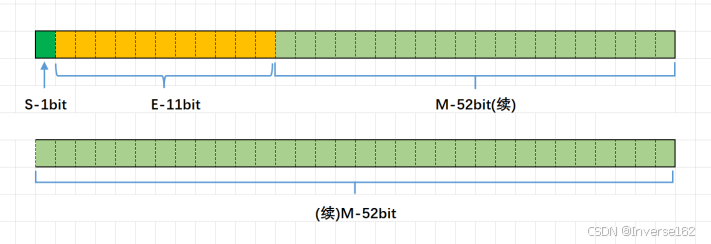
3.1 浮点数存的过程
关于有效数字 M:
M的取值范围是1 ≤ M < 2,M可以写成1.xxxxxx的形式,其中xxxxxx表示小数部分。
IEEE 754 规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以不用存储,只保存后面的xxxxxx部分,等到读取的时候再把第一位的1加上去。这样做可以节省1位有效数字。
以32位浮点数为例,留给M的只有23位,将第一位的1舍去之后,等于可以保存24位有效数字。
关于有效数字(指数)E:
E为一个无符号整数(unsigned int)。所以说如果E为8位,它的取值范围为0 ~ 255;如果E为11位,它的取值范围为0 ~ 2047。
众所周知,科学计数法中的E是可以出现负数的,所以IEEE 754规定,存入内存时E的真实值要加上一个中间数,对于8位的E,中间数为127;对于11位的E,中间数为1023。
例如:2^10的E是10,所以保存成32位浮点数时,必须保存成10 + 127 = 137,即10001001。
3.2 浮点数取的过程
指数E从内存中取出有3种情况:
1)E不全为0或不全为1:
浮点数采用上方的规则表示,指数E的存储值减去127(或1023),得到真实值,再将有效值M前加上第一位的1。
例如:0.5的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为1.0 × 2^(-1),其E在内存中的存储值为-1 + 127(中间值) = 126,表示为01111110,而尾数1.0去掉整数部分为0,补齐0到23位为00000000000000000000000,则其表示形式为:
0 01111110 00000000000000000000000
2)E全为0:
浮点数的指数E等于1 - 127(或1 - 1023)即为真实值,有效数字M不再加第一位的1,还原为0.xxxxxx的小数。这样做可以表示 ±0,以及接近于0的很小的数字。
0 00000000 00100000000000000000000
3)E全为1:
如果有效数字M全为0,表示 ±无穷大(S决定正负)。
0 11111111 00000000000000000000000