
欢迎来到我的:世界
希望作者的文章对你有所帮助,有不足的地方还请指正,大家一起学习交流 !?
目录
内容第一题:加一第二题:移动零第三题 :分发饼干第四题:买股票的最佳时机第五题:丢失的数字 总结
内容
再会
第一题:加一
地址:oj地址

解题思路:暴力求解
这道题就像是整形数字的十进一,因为是个数组,只要不是首位需要进位,其内存空间不需要改变,并且给最后位的元素+1
可分为以下几种情况:
1.个位需要进位:{1,2,9}+1={1,3,0};
2.除去首位的其他位的进位:{1,9,9}+1={2,0,0};
3.首位进位:{9,9,9}+1={1,0,0,0} (这种情况比较特殊,需要开辟一块原来空间+1的空间,并且所有元素赋值为0,最后首元素赋值1)
int* plusOne(int* digits, int digitsSize, int* returnSize) {//从个位开始遍历 for (int i = digitsSize - 1; i >= 0; i--) { //从个位+1,判断是否需要进位 digits[i] = digits[i] + 1; //如果个位+1后不为10,则可以直接返回数组 if (digits[i] != 10) { *returnSize = digitsSize; return digits; } else digits[i] = 0;//若为10,则可以把改为0 } //开辟一块比原来空间+1的空间,题目要求必须malloc函数开辟, int* pa = (int*)malloc(sizeof(int) * (digitsSize + 1)); //而malloc函数开辟的空间不会进行初始化,需要将空间所有元素赋值为0; memset(pa, 0, sizeof(int) * (digitsSize + 1)); pa[0] = 1;//既然首元素做高位进位,则直接赋值最高位为1即可; *returnSize = digitsSize + 1; return pa;}对这题其实判断元素是否为9,还是给元素+1后判断是否为10;这两种的思路解决方式是一样的,所以这里就不多嘴了,大家可以试一试另一种;
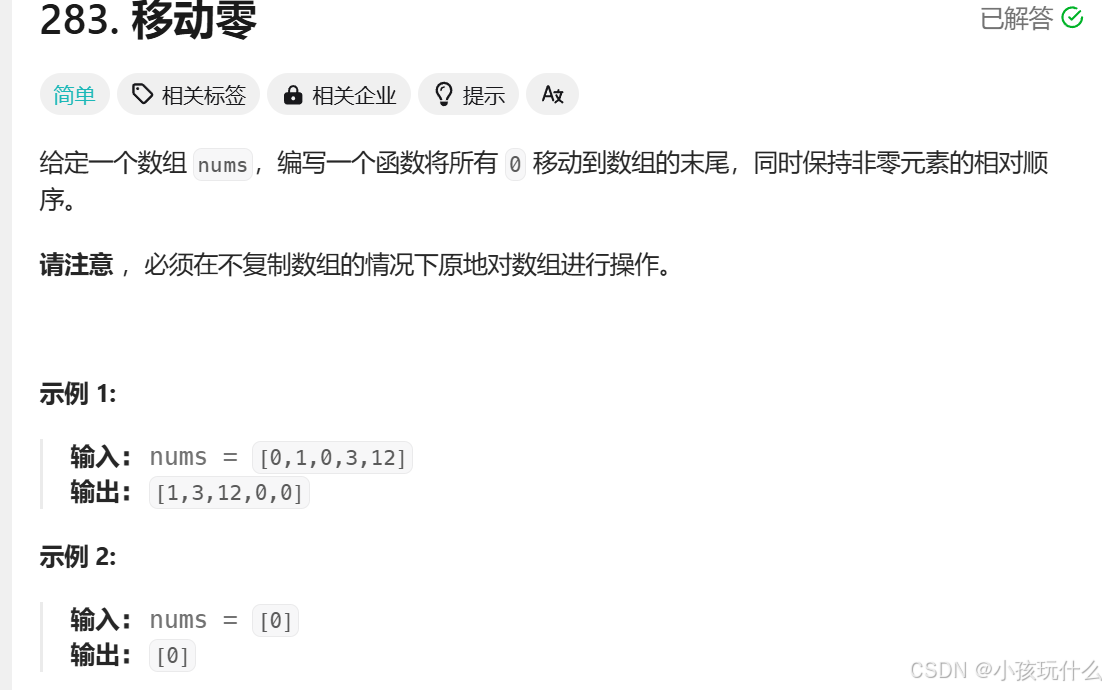
第二题:移动零
地址:oj地址
解题思路:
思路1:暴力求解:遍历一遍数组,遇到0就将0后面的元素一个一个往前覆盖,并且记录下0的个数x个,等所有元素遍历完,就将0从数组从后往前补x个;
思路2:双指针法:创建两个指针 j i,分别用于跟踪非零元素的位置和当前遍历到的位置,起始位置均为 0。j负责找非0的数值,i负责找0,在进行交换数值;
暴力求解:
void moveZeroes(int* nums, int numsSize) { // 计算数组中0的个数 int count = 0; int i = 0; int j = 0; //即在整个数组中遍历 while (j < numsSize) { //计算需要补零的个数 if (nums[j] == 0) { count++; } else { //遍历将不为0的数放置数组前方 nums[i] = nums[j]; i++; } j++; } //在后面补零 while (count--) { nums[j - 1] = 0; j--; }}双指针法:
void moveZeroes(int* nums, int numsSize) { int i=0,j=0; //开始遍历 while(j<numsSize) { //当j位置不为0时,进行交换 if(nums[j]) { int tem=nums[i]; nums[i]=nums[j]; nums[j]=tem; i++; } //当j位置为0时,继续往前走,直到找到0 j++; }}第三题 :分发饼干
地址:oj地址

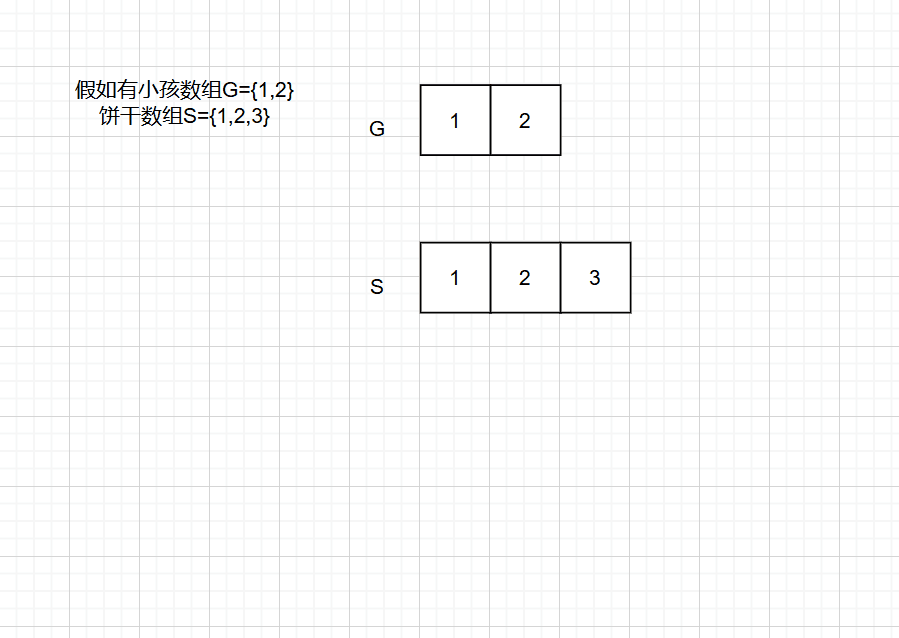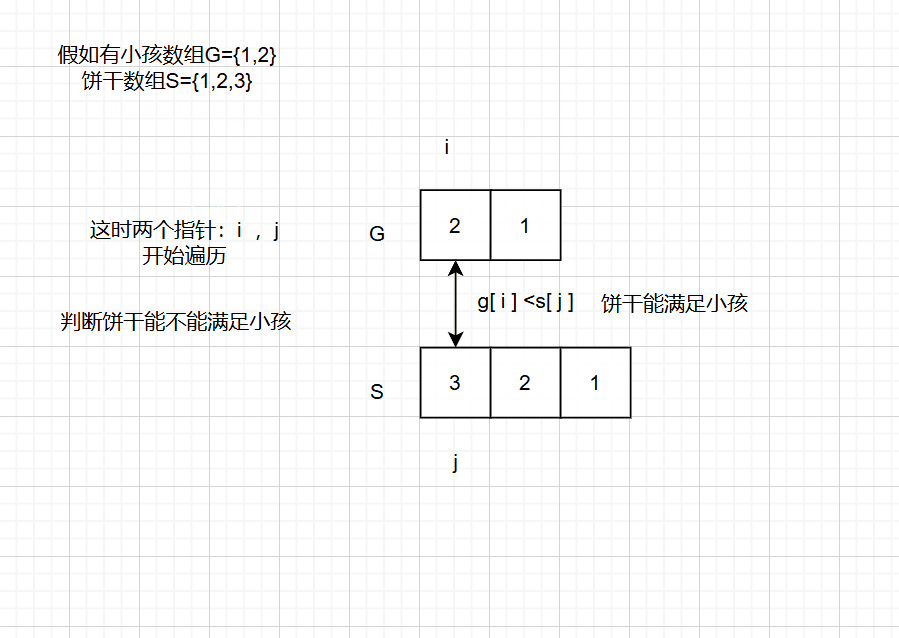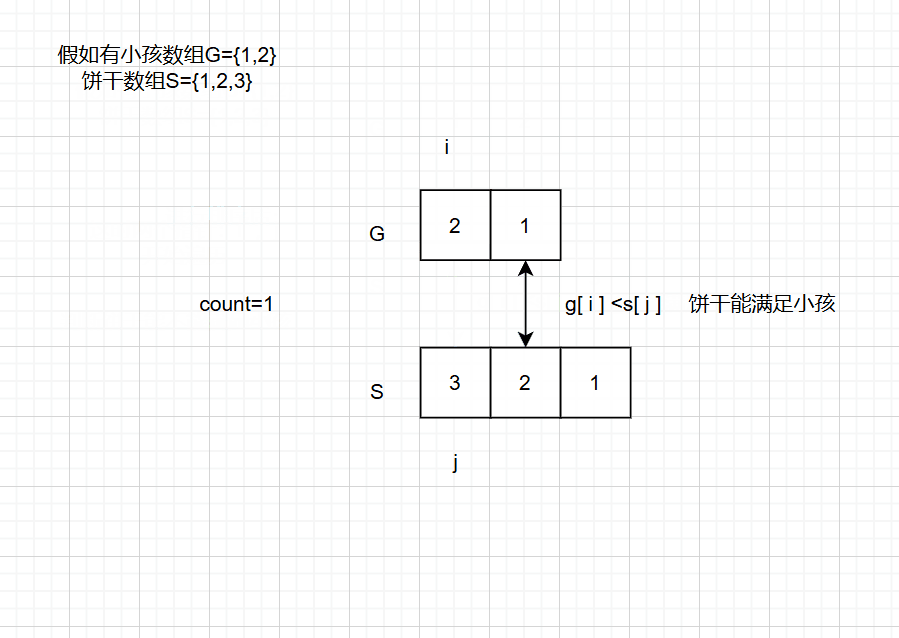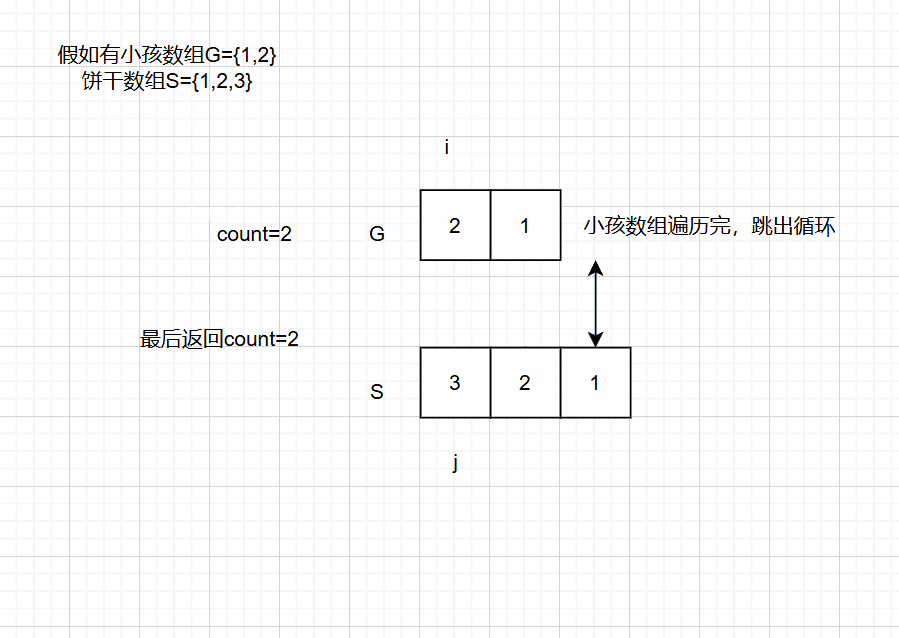
思路一:排序法::将两个数组g s进行由大到小排序,这样最大胃口的小孩,和最大尺寸的饼干都在数组开始了,这样能够更好的遍历,再创建一个记录满足小孩的个数count,在分别遍历两个数组,找到:s 数组饼干尺寸能满足 g数组的小孩胃口的饼干,若能满足,应该进行判断:不能跳出了饼干数组,则count ++,最后等饼干数组遍历完或者小孩数组遍历完,返回count
动画演示:
-
排序法实现:
int cmp(int* a, int* b) { return *a - *b;}int findContentChildren(int* g, int gSize, int* s, int sSize) {//进行排序 qsort(g, gSize, sizeof(int), cmp); qsort(s, sSize, sizeof(int), cmp); int m = gSize, n = sSize; //记录满足小孩的个数 int count = 0; //进入遍历 for (int i = 0, j = 0; i < m && j < n; i++, j++) { //找到能够满足最大胃口小孩的饼干 while (j < n && g[i] > s[j]) { j++; } //找到后,要判断,下标不能超过数组; if (j < n) { count++;//找到了能匹配的饼干和小孩,在往后去寻找,直到某个数组遍历完 } } return count;}第四题:买股票的最佳时机
地址:oj地址

第一种思路:暴力求解法::我们需要记录最小价格值,并且遍历后面的数值的价格 减去最小价格=利润,遍历完后最后的利润就是最大利润;
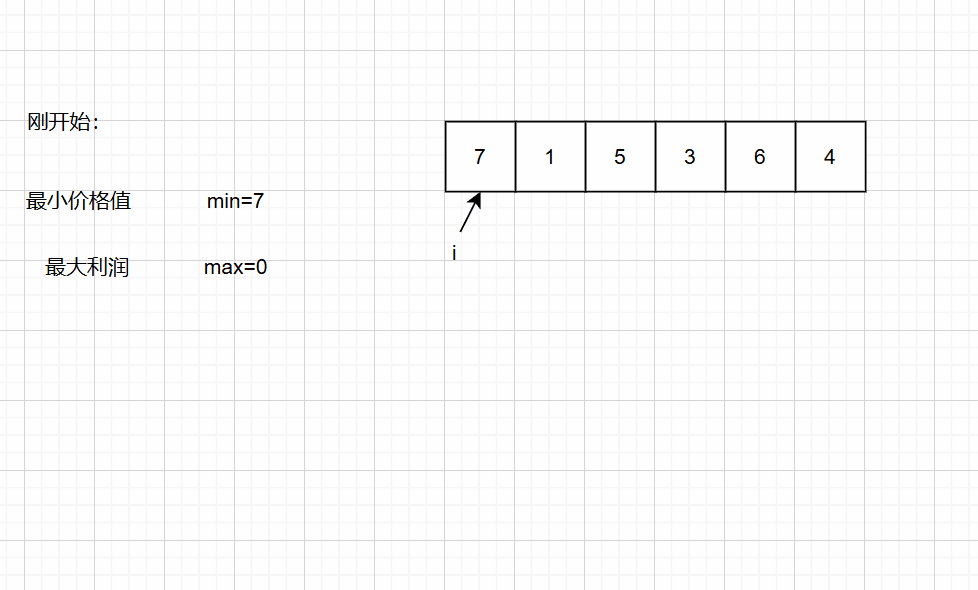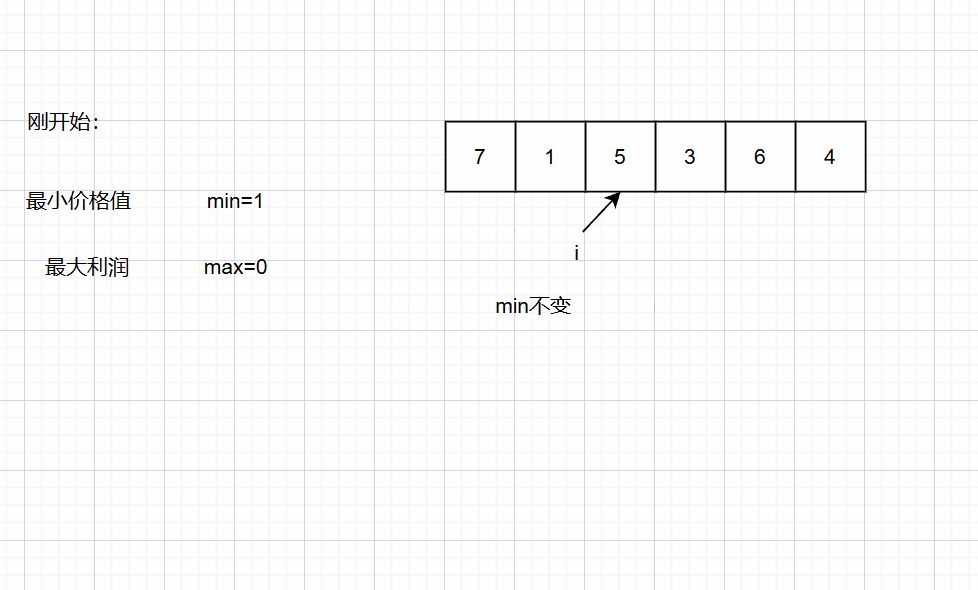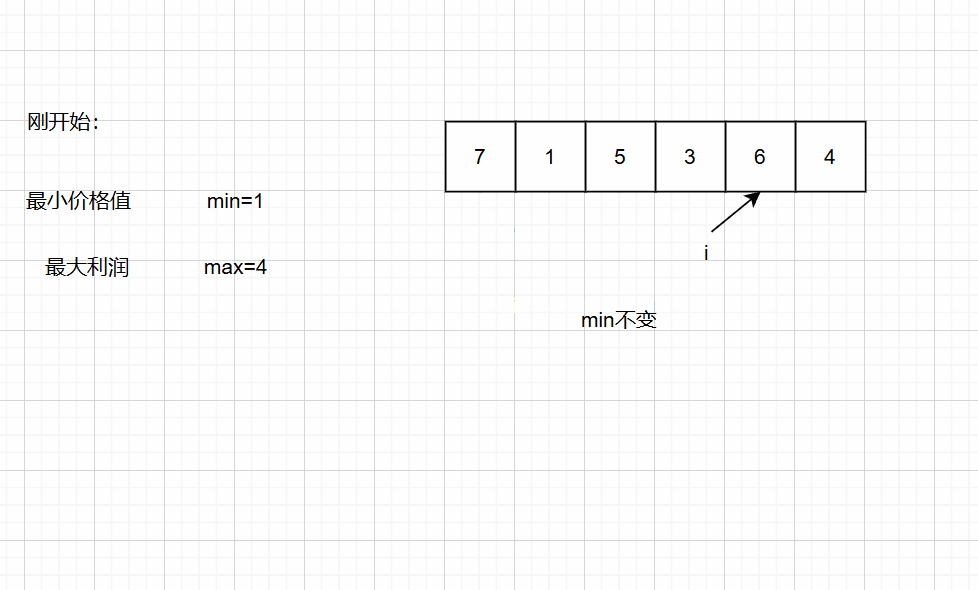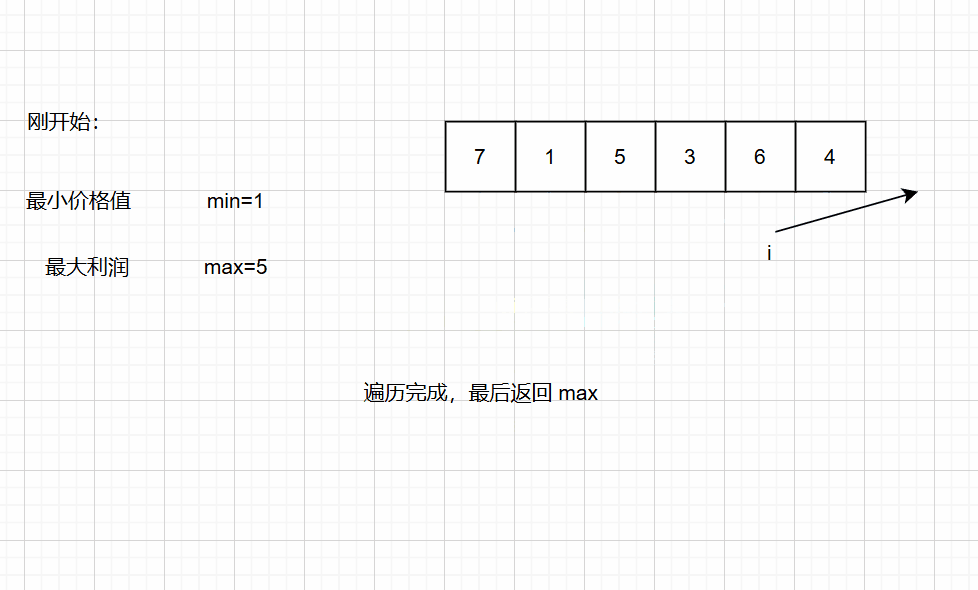
int maxProfit(int* prices, int pricesSize) { int min = prices[0];//假设这就是最小价格数值 int max = 0;//开始时设最大利润值为0 for (int i = 0; i < pricesSize; i++) { //遍历找那个最小的价格值 if (min > prices[i]) min = prices[i];//找出最大的利润值 if (prices[i] - min > max) max = prices[i] - min; } //返回最大利润值 return max;}第二种思路:暴力双层循环法:::我们需要找出给定数组中两个数字之间的最大差值(即,最大利润)。此外,第二个数字(卖出价格)必须大于第一个数字(买入价格)。
注意:这种方法在力扣上运行会超时
int maxProfit(int* prices, int pricesSize){ int max = 0; for (int i = 0; i < pricesSize-1; i++) { for (int j = i + 1; j < pricesSize; j++) { int ret = prices[j] - prices[i];//记录每次的利润,找出最大的利润 if (ret > max) { max = ret; } } } return max;}第五题:丢失的数字
地址:oj地址

思路:
暴力遍历法:将 0~n之间的数加起来在遍历减去nums数组的值,即可;
位运算法:根据出现的次数的奇偶性,可以使用按位异或运算得到丢失的数字:如有个数组[1,0,2,0,1]在这个数组中有些数组是成双出现的,根据 ^按位异或运算:且对任意整数x 都满足:x^x=0,x^0=0,可以将成双的数值互相消除,最后留下单身的那个;所以根据这个思路,可以将nums和0~n都看成数组,这两个数组进行按位异或操作,就可以得出最后的那个值;
暴力遍历法:
int missingNumber(int* nums, int numsSize) { int sum=0; for(int i=0;i<=numsSize;i++) { sum+=i; } for(int i=0;i<numsSize;i++) { sum-=nums[i]; } return sum;}对上代码可以这样优化:数学法:
int missingNumber(int* nums, int numsSize) {
int n=numsSize;
int total=n*(n+1)/2; //这里运用的数学的前n项求和
for(int i=0;i<numsSize;i++)
{
total-=nums[i];
}
return total;
}
对于上述代码我觉得可以写成这样:思路是和暴力一样的就是合并到了一个数组进行操作;
int missingNumber(int* nums, int numsSize) {
int sum=0;
for(int i=0;i<numsSize;i++)//这里判断条件 不能等于 否则会越界
{
sum+=(i-nums[i]);
}
return sum+numsSize; //
}
位运算法:
int missingNumber(int* nums, int numsSize) { int sum=0; for(int i=0;i<numsSize;i++)//这里判断条件 不能等于 否则会越界 { sum^=nums[i]; sum^=i; } sum^=numsSize; return sum;}
总结
到了最后:感谢支持
我还想告诉你的是:
------------对过程全力以赴,对结果淡然处之
也是对我自己讲的