引言
在人工智能(AI)和机器学习中,归一化(Normalization)是一个重要的预处理步骤。它的主要目的是将数据转换到某个特定的范围。归一化可以帮助模型更高效地学习和提高预测的准确性。归一化在数据预处理方法中占据核心地位,是确保数据质量和模型性能的关键步骤。
通过阅读本篇博客,你可以:
1.知晓归一化的概念
2.掌握常见的归一化方法
一、归一化的概念
1.归一化(Normalization)的目的
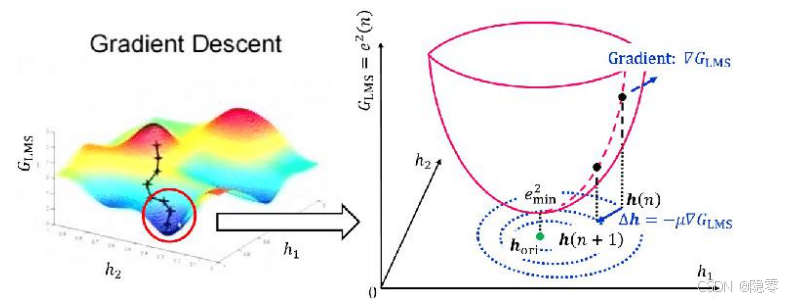
要讲归一化,我们不可避免的要提到梯度下降。如果维度过多(超平面),我们很难将其以不同参数的关系表达出来。所以我们使用两个维度作为例子来阐述归一化前与归一化后的区别。如果拿多元线性回归距离,因为多元线性回归的损失函数MSE是凸函数,所以我们把损失函数看成一个碗,损失最小的地方就是碗底的地方(如上图所示)。
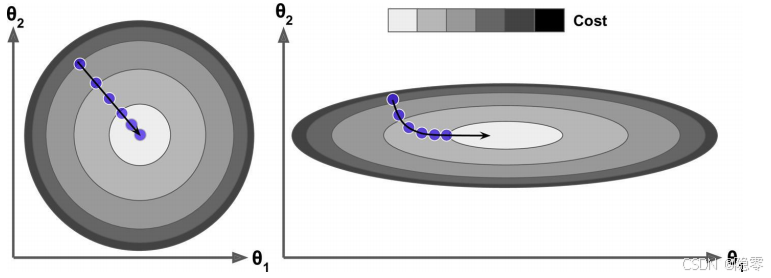
上图左是做了归一化的俯瞰图,上图右是没有做归一化的俯瞰图。
"为什么没有做归一化的俯瞰图会显示为椭圆形呢?"。为了回答这个问题,我们不妨设置一些变量用于证明。假设维度 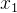 中的每一条数据都远小于维度
中的每一条数据都远小于维度 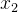 中的每一条数据 ,即
中的每一条数据 ,即 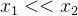 。我们将表达式的截距项设为0。那么整个表达式即为
。我们将表达式的截距项设为0。那么整个表达式即为 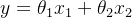 。因为我们不知道两个维度权重的大小,所以我们可以想象两部分对
。因为我们不知道两个维度权重的大小,所以我们可以想象两部分对 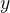 的贡献是一样的,即
的贡献是一样的,即 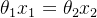 ,又由于
,又由于 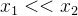 ,最终能得出
,最终能得出 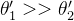 。所以说上右图中
。所以说上右图中 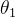 的轴要比
的轴要比 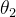 的轴长,且俯瞰图呈椭圆形。再次思考一下,我们在梯度下降的第一步中,所有的
的轴长,且俯瞰图呈椭圆形。再次思考一下,我们在梯度下降的第一步中,所有的 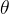 都是服从标准正态分布分布的,也就是初始的
都是服从标准正态分布分布的,也就是初始的 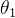 和
和 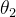 是差不多的。所以我们可以得出结论:
是差不多的。所以我们可以得出结论: 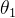 从 初始值到目标位置
从 初始值到目标位置 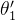 的距离要远大于
的距离要远大于 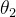 从初始值到目标位置
从初始值到目标位置 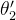 ,也就是调整幅度
,也就是调整幅度 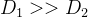 。
。
从公式的角度去推导,从梯度计算公式 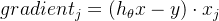 中我们可以知道,梯度与样本
中我们可以知道,梯度与样本 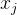 呈正比,所以
呈正比,所以 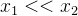 可以推导出
可以推导出 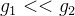 。又由于梯度下降公式
。又由于梯度下降公式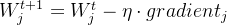 ,所以我们能得出结论:每次
,所以我们能得出结论:每次 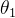 的调整幅度要远小于
的调整幅度要远小于 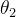 的调整幅度。
的调整幅度。
根据上述的两个结论,我们可以发现, 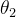 的路程更短,但是步幅更长,意味着相比较
的路程更短,但是步幅更长,意味着相比较 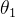 ,
,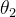 只需要用更少的迭代次数就可以收敛。而我们为了求得最优解,就必须每个维度的
只需要用更少的迭代次数就可以收敛。而我们为了求得最优解,就必须每个维度的 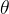 都收敛才可以,所以就会出现
都收敛才可以,所以就会出现 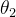 等待
等待 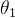 的情况。这就是右上图中
的情况。这就是右上图中 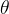 先往下走再往右走的原因。
先往下走再往右走的原因。
我们使用归一化的目的就是使得梯度下降的时候可以让不同维度的 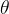 参数都在较为接近的调整幅度上。这就好比社会主义,先使一小部分的人富起来,使损失整体下降,最后等另一部分人富起来。但是更好的情况其实是实现共同富裕,每个人都不落下,让优化的步伐是一致的(如左上图所示)。
参数都在较为接近的调整幅度上。这就好比社会主义,先使一小部分的人富起来,使损失整体下降,最后等另一部分人富起来。但是更好的情况其实是实现共同富裕,每个人都不落下,让优化的步伐是一致的(如左上图所示)。
2.归一化(Normalization)的本质
归一化的本质是将数据转换到统一的尺度上,使得不同特征或数据点之间具有可比性,简化了数据处理的复杂性,并提高了算法的效率和稳定性。
我们现在知道了归一化的目的是让每个维度的参数共同富裕。梯度下降优化时不能达到步调一致的根本原因其实还是 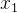 和
和 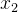 的数量级不同。而归一化可以把
的数量级不同。而归一化可以把 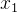 和
和 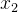 的数量级给它统一,扩展一点说,如果有更多特征维度,就要把各个特征维度
的数量级给它统一,扩展一点说,如果有更多特征维度,就要把各个特征维度 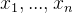 的数量级统一,来做到无量纲化。
的数量级统一,来做到无量纲化。
二、常见的归一化方法
接下来我们来介绍两种常见的归一化方法。
1.最大值最小值归一化
最大值最小值归一化(Min-Max Scaling)可以将数据映射到特定的区间,如[0,1]或[-1,1]。它的公式为:
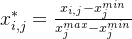
在这个公式当中,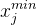 对应着
对应着 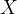 矩阵中第
矩阵中第 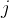 列特征值中的最小值。同样地,
列特征值中的最小值。同样地,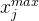 是对应
是对应 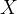 矩阵中第
矩阵中第 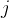 列特征值中的最大值。
列特征值中的最大值。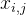 是
是 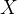 矩阵中第
矩阵中第 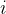 行第
行第 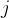 列的数值,
列的数值,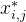 是归一化之后的
是归一化之后的 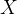 矩阵中第
矩阵中第 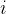 行第
行第 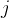 列的数值。
列的数值。
举个例子,比如第 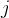 列的数值是
列的数值是 ![[1,2,3,5,5]](http://zhangshiyu.com/zb_users/upload/2024/10/20241025144132172983849294266.png) ,
, 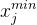 就是 1,
就是 1,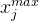 就是 5,那么归一化 之后是
就是 5,那么归一化 之后是 ![[0,0.25,0.75,1,1]](http://zhangshiyu.com/zb_users/upload/2024/10/20241025144132172983849298464.png) 。如果第
。如果第 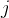 列的数值是
列的数值是 ![[1,2,3,5,50001]](http://zhangshiyu.com/zb_users/upload/2024/10/20241025144132172983849292553.png) ,那么归一化之后是
,那么归一化之后是![[0,0.00004,0.00006,0.0001,1]](http://zhangshiyu.com/zb_users/upload/2024/10/20241025144133172983849375845.png) 。
。
从这个例子中我们可以很容易地发现,使用最大值最小值归一化的时候,优点是一定可以把数值归一化到 ![[0,1]](http://zhangshiyu.com/zb_users/upload/2024/10/20241025144133172983849397340.png) ,缺点是如果有离散值,会使一个数值为1,其它数值几乎为0,所以受到离散值的影响比较大。
,缺点是如果有离散值,会使一个数值为1,其它数值几乎为0,所以受到离散值的影响比较大。
2.标准归一化
通常标准归一化中包含了均值归一化和方差归一化。经过处理的数据符合标准正态分布,即均值为0,标准差为1,其转化函数为:
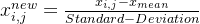
我们也通常将其表示成:
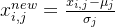
其中 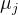 为某列样本数据的均值,
为某列样本数据的均值,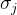 为某列样本数据的标准差。
为某列样本数据的标准差。
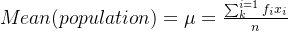
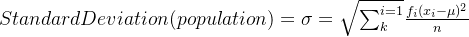
其中的 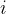 为行数,
为行数,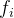 为不同行中
为不同行中 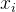 的权重,这里我们可以默认将其看作是 1 。
的权重,这里我们可以默认将其看作是 1 。
相对于最大值最小值归一化公式计算机时除以最大值减最小值来说,标准归一化除以的是标准差,而标准差的的计算会考虑到本列样本中的所有样本数据,这样受到离群值的影响就会小很多。这就是方差归一化的好处。
那么我们为什么要减去均值呢?我们可以通过下图来看出。 下左图是梯度下降法的公式,其中 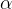 代表学习率,
代表学习率,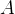 代表梯度计算中的
代表梯度计算中的 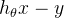 (详情请阅读博客12.梯度下降法的具体解析——举足轻重的模型优化算法-CSDN博客)。我们可以从中看出,当
(详情请阅读博客12.梯度下降法的具体解析——举足轻重的模型优化算法-CSDN博客)。我们可以从中看出,当 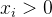 时,所有维度的梯度都是朝着一个方向前进的,因为每个维度的学习率
时,所有维度的梯度都是朝着一个方向前进的,因为每个维度的学习率 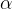 和误差
和误差 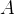 都是相同的,这就导致了下右图的问题。当我们想将梯度从
都是相同的,这就导致了下右图的问题。当我们想将梯度从 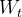 变为
变为 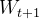 时,维度1中的
时,维度1中的 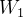 在下降,维度2中的
在下降,维度2中的  在增加,这就跟我们左图所说的方法相违背。所以我们只能整体的先全部增加,再整体的全部下降,呈现出右下图三角形的另外两边,不能实现图上蓝色所示的最优路径,这样就浪费了我们很多迭代次数和时间。归其根本,还是大多数数据集的数据均为正数,所以我们减去均值,就是给梯度下降法的方向增加更多可能性,减少更多的迭代次数,这就是均值归一化的好处。
在增加,这就跟我们左图所说的方法相违背。所以我们只能整体的先全部增加,再整体的全部下降,呈现出右下图三角形的另外两边,不能实现图上蓝色所示的最优路径,这样就浪费了我们很多迭代次数和时间。归其根本,还是大多数数据集的数据均为正数,所以我们减去均值,就是给梯度下降法的方向增加更多可能性,减少更多的迭代次数,这就是均值归一化的好处。
总结
本篇博客重点介绍了归一化这种数据预处理方法。希望可以对大家起到作用,谢谢。
关注我,内容持续更新(后续内容在作者专栏《从零基础到AI算法工程师》)!!!
