
博客主页:【夜泉_ly】
本文专栏:【C++】
欢迎点赞?收藏⭐关注❤️

文章目录
? 简介1. 栈2. 队列3. 容器适配器的特点4. 适配器的本质5. 小结 ? 简单实现1. 栈的实现2. 队列的实现 ? 简单使用1. 用队列实现栈1 题目描述2 代码实现1 逻辑详解代码总结 3 代码实现2 逻辑详解代码总结 2. 用栈实现队列1 题目描述2 逻辑详解3 代码实现4 总结
? 简介
栈(Stack)和队列(Queue)是两种常用的数据结构,它们在使用上相对简单,但却在计算机科学中扮演着重要的角色。它们的核心特性和行为使得它们在特定场景下比其他数据结构(如向量或链表)更具优势。
在数据结构-栈、队列-详解中,我用C语言模拟实现了栈和队列,感兴趣的可以去看看。
1. 栈
栈是一种容器适配器,其工作原理类似于电源适配器对电压的转换,但其内部使用的仍然是其他容器。

栈的默认底层容器是deque(双端队列),但也可以用其他容器实现栈的功能。
栈的核心特点是遵循后进先出(LIFO)原则,即最后入栈的数据最先出栈。栈的基本操作包括:
top:获取栈顶元素,但不移除它。

push:将数据压入栈中。

pop:移除栈顶元素并返回其值。

通过这三种操作,栈能够有效地管理数据,适用于递归算法、表达式求值等场景。
?例如《剑指offer》面试题6:从尾到头打印链表。
就可以使用栈 后进先出 的特性来完成。
2. 队列
队列同样是一种容器适配器,主要用于按照先进先出(FIFO)原则处理数据。

与栈不同,队列允许数据在一端插入(入队)并从另一端移除(出队)。队列的核心操作包括:
push:将数据入队。

pop:移除队首元素并返回其值。

front:获取队首元素,但不移除它。

back:获取队尾元素,但不移除它。

队列可以用于广度优先搜索,例如二叉树的层序遍历。
3. 容器适配器的特点
作为容器适配器,栈和队列并没有提供迭代器。这是因为它们不支持随意遍历元素,必须严格遵循LIFO或FIFO的规则。这种设计确保了数据的顺序性和结构的完整性。
此外,容器适配器通过封装底层容器,提供了更加简单易用的接口,使得开发者能够专注于数据操作,而无需关心内部实现的复杂性。
4. 适配器的本质
⭕适配器的本质是复用
例如容器适配器封装了其他的容器,数据存储在这个容器里面,而容器适配器会根据要求适配出对应的接口。
通过适配器,开发者可以使用不同的数据结构实现特定的行为,而无需重新实现算法或接口。这种灵活性大大提高了代码的复用性和可维护性。
在栈和队列的实现中,适配器模式使得其行为符合实际需求,同时又保持了与其他容器的兼容性。
5. 小结
综上所述,栈和队列作为基本的数据结构,在编程中发挥着重要的作用。理解它们的特点和使用场景,可以帮助开发者在实际应用中更有效地选择合适的数据结构,提升代码的效率与可读性。在今后的编程实践中,掌握栈和队列的使用无疑将为解决复杂问题提供有效的支持。
? 简单实现
?C语言版:数据结构-栈、队列-详解
1. 栈的实现
适配器是对已有的东西进行适配、转换。在 C 语言中模拟实现一个栈时,需要考虑是用数组实现还是用链表实现。
这就引出了一个问题:如何做到数组栈和链式栈的快速切换?
在 C++ 中,可以使用模板类来实现这一点:
namespace ly{template<class T, class Container>class stack{public:// ...private:Container _con;}}这里用Container定义了一个容器,至于这个容器具体是什么,不知道。
但这就是想要达到的目的,因为使用更加灵活了:
void test_stack(){ly::stack<int, std::vector<int>> st1;ly::stack<int, std::list<int>> st2;}可以看见,即可以用 vector 实现, 也可以用 list 实现,这取决于传的是什么容器。
下面我将继续完善这个栈:
使用容器的插入、删除方法void push(const T& value) { _con.push_back(value); }void pop() { _con.pop_back(); }返回栈顶元素T top() const { return _con.back(); } ⭕值得一提的是这里不能用 [ ],因为 list 不支持[]。
bool empty() const { return _con.empty(); }返回栈的大小size_t size() const { return _con.size(); } 这就完了?,很简单吧。
并且数组栈、链式栈在用的角度没有区别,还能做到秒切换。
以下是一个简单的测试函数,演示如何使用这个栈:
void test_stack(){// 使用 vector 实现的栈ly::stack<int, std::vector<int>> vecStack; vecStack.push(1);vecStack.push(2);vecStack.push(3);std::cout << " vecStack:";while (!vecStack.empty()){std::cout << vecStack.top() << " "; // 输出栈顶元素vecStack.pop(); // 弹出栈顶元素}std::cout << std::endl;// 使用 list 实现的栈ly::stack<int, std::list<int>> listStack; listStack.push(1);listStack.push(2);listStack.push(3);std::cout << "listStack:";while (!listStack.empty()){std::cout << listStack.top() << " "; // 输出栈顶元素listStack.pop(); // 弹出栈顶元素}}Output:
vecStack:3 2 1listStack:3 2 1每次传模板参数比较麻烦,因此库里面也没要求每次都传:

deque 是什么,在我之后的文章中会讲。
这里可以直接给 vector:
template<class T, class Container = vector<T>>⭕栈需不需要提供构造、析构?
不用,因为这是自定义类型,它会调用自己成员的构造、析构。而容器是已经实现好的,构造、析构就是现成的。
2. 队列的实现
大部分类似于栈的实现,这里直接引出问题:队列能不能用 vector 适配?可以,但不推荐。
强制适配:
void pop(){ _con.erase(_con.begin());}erase 是 list 和 vector 都提供的接口,因此能用。
但这样强制适配好吗?这样不好。
如果在VS写出下面这几句代码:
std::queue<int, vector<int>> q; q.push(1);q.pop();再运行:
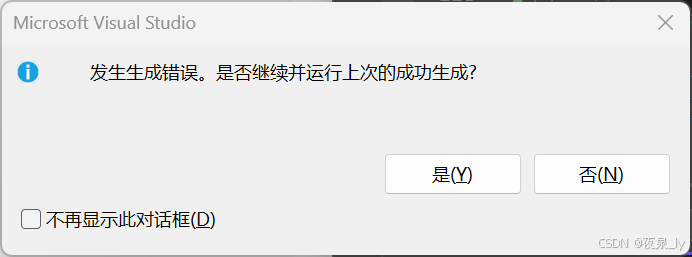

⭕库里面支持list,不支持vector。
⭕库里面pop调的pop_front,而vector没有pop_front。
? 简单使用
下面的题目我在数据结构-栈、队列-相关练习中曾经讲过,不过是用C语言写的,有兴趣的可以去看看。
1. 用队列实现栈
题目链接:
225. 用队列实现栈
(https://leetcode.cn/problems/implement-stack-using-queues/description/)
1 题目描述
在此问题中,需要实现一个栈(Stack),但仅允许使用队列(Queue)来完成操作。

并且题目指出:
你只能使用队列的标准操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
栈是一种后进先出(LIFO)的数据结构,而队列是一种先进先出(FIFO)的数据结构。
因此,必须通过一些巧妙的方式,利用队列的特性来模拟出栈的行为。
2 代码实现1
逻辑详解
数据成员
根据题目要求,该类有两个队列queue1 和 queue2,用于存储栈的元素。可以根据队列的大小和使用情况选择其中一个进行操作。 构造函数
MyStack 的构造函数是空的,因为这个类的实例并不需要初始化其他内容。 push
当调用push 时,如果 queue1 为空,则将元素 x 放入 queue2 中,否则放入 queue1 中。 这一步其实也可以就用一个队列来入元素,但我当时没这么想。
pop
pop 方法是最关键的函数。它负责从当前的主队列中弹出元素。首先检查 queue2 是否为空: 如果为空,则表示当前的 queue1 是操作的主队列。将 queue1 中除了最后一个元素外的所有元素依次转移到 queue2 中,直到 queue1 只剩一个元素。取出 queue1 中的最后一个元素(即要弹出的元素),并将其返回。 如果 queue2 不为空,操作类似,从 queue2 转移到 queue1。 这一设计确保了最后被放入的元素总是能在 pop() 方法中被弹出,符合栈的特性。
top
top 返回当前栈顶的元素而不移除它。它会检查 queue1 和 queue2,返回非空队列的最后一个元素(即栈顶元素)。
empty
empty 方法用来检查栈是否为空。检查两个队列是否都为空就行。
代码
以下是实现的代码:
class MyQueue { stack<int> stackPush; stack<int> stackPop;public: MyQueue() {} void checkSTPopEmpty() { if(stackPop.empty()) { while(!stackPush.empty()) { stackPop.push(stackPush.top()); stackPush.pop(); } } } void push(int x) { stackPush.push(x); } int pop() { checkSTPopEmpty(); int tmp = stackPop.top(); stackPop.pop(); return tmp; } int top() { checkSTPopEmpty(); return stackPop.top(); } bool empty() { return stackPop.empty()&&stackPush.empty(); }};总结
这个实现利用了两个队列通过转移元素的方式来模拟栈的行为,相对高效。push 操作的平均时间复杂度为 O(1),而 pop 和 top 操作的平均时间复杂度为 O(1)。尽管个别操作可能在转移时有 O(n) 的复杂度,但整体表现是非常好的。
但是在空间上,题目提出了进一步的要求:
进阶:你能否仅用一个队列来实现栈。
3 代码实现2
相信只要会用两个队列实现,很快就能想到用一个队列实现的方法。
逻辑详解
要仅使用一个队列来实现队列的功能,可以采用一种不同的策略:在 push 操作时,将新元素加入队列的末尾,然后通过队列中的元素调整队列,以保持后进先出的顺序。
数据成员
根据题目要求,仅使用一个队列queue1 来存储所有的元素。 构造函数
MyQueue 的构造函数为空,无需额外初始化。 push
首先,将元素x 放入 queue1 的末尾。然后,通过循环,将队列中除新加入的元素外的其他元素依次移到队列的末尾。这样可以确保队列的顺序满足先进先出的特性,即最新加入的元素总是位于队列的前端。 pop
直接从队列的前端弹出元素,并返回该元素。top
返回队列前端的元素,但不从队列中移除它。empty
检查queue1 是否为空,以确定队列是否为空。 代码
以下是实现的代码:
class MyStack { queue<int> queue1;public: MyStack() {} void push(int x) { queue1.push(x); for (int i = 0; i < queue1.size() - 1; i++) { queue1.push(queue1.front()); queue1.pop(); } } int pop() { int tmp = queue1.front(); queue1.pop(); return tmp; } int top() { return queue1.front();} bool empty() { return queue1.empty();}};总结
这种方法虽然可以使用单个队列来实现队列的功能,但在 push 操作中,由于需要调整队列中所有元素的位置,因此时间复杂度为 O(n)。
相较于使用两个栈或两个队列的方法,该实现可能在性能上有所下降。
但它展现了如何使用基础数据结构的灵活性来实现特定功能。
2. 用栈实现队列
题目链接:
232. 用栈实现队列
(https://leetcode.cn/problems/implement-queue-using-stacks/description/)
1 题目描述
在此问题中,需要实现一个队列,但仅允许使用栈来完成操作。

队列是先进先出(FIFO)的数据结构,而栈是后进先出(LIFO)的数据结构。
因此,和前面的题目一样,需要利用栈的特性来模拟队列的行为。
2 逻辑详解
数据成员
这个类有两个栈 stackPush 和 stackPop,分别用于存储加入队列的元素和用于弹出的元素。
构造函数
MyQueue 的构造函数是空的,实例的初始化不需要额外的设置。
checkSTPopEmpty
这是一个辅助函数,负责检查stackPop 是否为空。如果为空,则将 stackPush 中的所有元素逐个弹出并推入到 stackPop 中。这样确保了最新入栈的元素在 stackPop 中的最上面,符合队列的先入先出特性。 push
该方法简单地将元素x 推入 stackPush 中。所有的新元素都会在 stackPush 中存储。 pop
当调用pop() 时,首先调用 checkSTPopEmpty 来确保 stackPop 中有元素可以弹出。然后从 stackPop 中弹出并返回栈顶元素。 peek
peek 方法同样使用 checkSTPopEmpty() 确保 stackPop 中有元素,然后返回栈顶元素而不移除它。 empty
检查两个栈是否都为空,以判断队列是否为空。3 代码实现
以下是实现的代码:
class MyQueue { stack<int> stackPush; stack<int> stackPop; public: MyQueue() {} void checkSTPopEmpty() { if(stackPop.empty()) { while(!stackPush.empty()) { stackPop.push(stackPush.top()); stackPush.pop(); } } } void push(int x) { stackPush.push(x); } int pop() { checkSTPopEmpty(); int tmp = stackPop.top(); stackPop.pop(); return tmp; } int peek() { checkSTPopEmpty(); return stackPop.top(); } bool empty() { return stackPop.empty()&&stackPush.empty(); }};4 总结
使用两个栈的实现方法来模拟队列有效地解决了先进先出的问题。push 操作的时间复杂度为 O(1),而 pop 和 peek 操作的平均时间复杂度为 O(1),在最坏的情况下可能需要 O(n) 的时间进行转移,但整体性能仍然可以接受。
希望本篇文章对你有所帮助!并激发你进一步探索编程的兴趣!
本人仅是个C语言初学者,如果你有任何疑问或建议,欢迎随时留言讨论!让我们一起学习,共同进步!