文章目录
C++ 双指针详解:基础题解与思维分析前言第一章:对撞指针1.1 移动零解题思路图解分析C++代码实现易错点提示代码解读 1.2 复写零解题思路算法步骤C++代码实现易错点提示代码复杂度 1.3 盛最多水的容器1. 题目链接2. 题目描述解法一(暴力求解)解法二(对撞指针)易错点提示复杂度对比与结论小结 第二章:快慢指针 2.1 复写零题目链接题目描述题目分析解法(快慢指针)C++代码实现代码解析易错点提示复杂度分析 写在最后
C++ 双指针详解:基础题解与思维分析
? 欢迎讨论:如有疑问或见解,欢迎在评论区留言互动。
? 点赞、收藏与分享:如觉得这篇文章对您有帮助,请点赞、收藏并分享!
? 分享给更多人:欢迎分享给更多对 C++ 感兴趣的朋友,一起学习双指针的基础与进阶!
前言
双指针方法是一种常见且高效的算法技巧,常用于数组和链表问题的优化解决。在这一篇博客中,我们将通过详细的讲解和题目解析,帮助大家理解双指针的基础用法及其应用场景。
第一章:对撞指针
1.1 移动零
题目链接:283. 移动零
题目描述:给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
解题思路
此题的主要思路是通过双指针法,使所有非零元素依次移动到数组前部,零元素则自动归到数组的后部。具体思路如下:
初始化两个指针:
cur:遍历整个数组。dest:指向最后一个非零元素的位置,初始化为 -1。(因为不知道数组第一个元素是不是0) 遍历数组:
如果cur 指向非零元素,并且++dest!=cur,则将其放置在 dest + 1 的位置。当 cur 遇到 0 时,不做任何操作,只移动 cur。 结束条件:
当cur 遍历完整个数组后,dest + 1 后的所有位置自动归零,完成所需操作。 图解分析
假设数组初始为 [0, 1, 0, 3, 12]:
初始状态:
cur = 0,dest = -1。因为 nums[cur] 是 0,cur 右移,dest 保持不动。 步骤 1:
cur = 1,nums[cur] = 1。dest = -1,非零元素 1 应插入到 dest + 1 = 0 位置上。交换 nums[++dest] 和 nums[cur],即 nums[0] 和 nums[1],数组变为 [1, 0, 0, 3, 12]。 步骤 2:
cur = 3,nums[cur] = 3。此时 dest = 1。将 3 插入 dest + 1 = 2 位置上,交换后数组变为 [1, 3, 0, 0, 12]。 步骤 3:
cur = 4,nums[cur] = 12。此时 dest = 2。将 12 插入 dest + 1 = 3 位置上,交换后数组变为 [1, 3, 12, 0, 0]。 步骤图解:
| Iteration | cur Pointer | dest Pointer | Array State |
|---|---|---|---|
| 1 | 0 | -1 | [0, 1, 0, 3, 12] |
| 2 | 1 | 0 | [1, 0, 0, 3, 12] |
| 3 | 3 | 1 | [1, 3, 0, 0, 12] |
| 4 | 4 | 2 | [1, 3, 12, 0, 0] |
C++代码实现
class Solution {public: void moveZeroes(vector<int>& nums) { for (int cur = 0, dest = -1; cur < nums.size(); cur++) { if (nums[cur] != 0&&++dest!= cur) { swap(nums[dest], nums[cur]); } } }};易错点提示
指针初始化:dest 从 -1 开始,以便于将第一个非零元素移动到 0 位置。交换顺序:应确保 ++dest 和 cur 指向的元素交换,否则会造成非零元素错位。理解条件判断:nums[cur] 为非零时才交换,避免多余的操作。 代码解读
在代码执行中,非零元素会依次覆盖零元素的位置,最终达到将所有零移动到数组末尾的目的。此方法的时间复杂度为 O(n),空间复杂度为 O(1),即为原地操作,不占用额外空间。
这个⽅法是往后我们学习「快排算法」的时候,「数据划分」过程的重要⼀步。如果将快排算法拆解的话,这⼀段⼩代码就是实现快排算法的「核⼼步骤」。
1.2 复写零
题目链接:1089. 复写零
题目描述:给定一个固定长度的整数数组 arr,在遇到每个零时,将其右移并插入一个零,同时保持数组长度不变。
解题思路
因为数组的零元素会被重复写入两次,如果直接从前向后遍历会导致覆盖,因而最优解是使用双指针从后往前复写。算法分为两步:
找出最后一个需要复写的元素:从头到尾遍历数组,计算复写位置。逆序复写数组:从最后一个元素开始向前,将每个零复写到目标位置,同时不覆盖后续元素。算法步骤
初始化指针:
cur:用来找到被复写后数组的最后一个数在原来数组的位置,初始化为0dest:用于模拟复写过程,初始为 -1。 寻找最后一个需要复写的元素:
使用cur 遍历数组: 如果 arr[cur] 非零,则 dest++。如果 arr[cur] 为零,则 dest += 2。 若 dest 大于或等于 n - 1(数组最后一个位置),则退出循环。 处理越界情况:
如果dest == n,表示需要在最后填入一个零。此时,将 arr[n - 1] 设置为零,并调整 cur-- 和 dest -= 2 以适应边界复写。 从后向前完成复写操作:
使用逆序遍历从cur 开始复写至 dest,若 arr[cur] 为零则复写两次,否则只复写一次。 C++代码实现
class Solution {public: void duplicateZeros(vector<int>& arr) { int cur = 0, dest = -1, n = arr.size(); // 1. 寻找最后一个需要复写的数 while (cur < n) { if (arr[cur]) dest++; // 非零元素,dest 右移一位 else dest += 2; // 遇零时,dest 右移两位 if (dest >= n - 1) break; // 越界则退出循环 cur++; } // 2. 处理边界情况,dest == n 时需在末尾填零 if (dest == n) { arr[n - 1] = 0; cur--; dest -= 2; } // 3. 从后向前复写元素 while (cur >= 0) { if (arr[cur]) { arr[dest--] = arr[cur]; // 非零元素,复写到 dest 位置 } else { arr[dest--] = 0; // 遇到零时,连续写两次 arr[dest--] = 0; } cur--; } }};假设数组为 arr = [1, 0, 2, 3, 0, 4, 5, 0]:
步骤 1:找到最后一个需要复写的元素
初始化cur = 0,dest = -1,n = 8遍历数组,遇到零元素时 dest 向后移动两位,遇到非零元素时 dest 向后移动一位。目标是找到最后一个需要复写的元素位置 cur。 int cur = 0, dest = -1, n = arr.size();while (cur < n) { if (arr[cur]) dest++; // 非零元素 else dest += 2; // 零元素,移动两位 if (dest >= n - 1) break; cur++;}遍历示例:
cur = 0,arr[0] = 1,dest++,所以 dest = 0cur = 1,arr[1] = 0,dest += 2,所以 dest = 2依此类推,最终 cur = 5,dest = 7,在此位置结束循环。 步骤 2:逆序填充
在此时,cur 为 5,dest 为 7。从这两个位置开始逆序复写,以避免前面的零覆盖其他元素:
| Iteration | cur | dest | Array State |
|---|---|---|---|
| Start | 5 | 7 | [1, 0, 2, 3, 0, 4, 5, 0] |
| 1 | 4 | 6 | [1, 0, 2, 3, 0, 4, 5, 4] |
| 2 | 3 | 3 | [1, 0, 2, 3, 0, 0, 0, 4] |
| 4 | 1 | 2 | [1, 0, 2, 2, 3, 0, 0, 0] |
| 5 | 1 | 2 | [1, 0, 0, 2, 3, 0, 0, 0] |
| Final | 0 | 1 | [1, 0, 0, 2, 3, 0, 0, 4] |
具体操作解释:
开始:cur = 5,dest = 7,将 arr[5] 的值 4 复制到 arr[7]。遇到零:cur = 4,在 arr[6] 和 arr[5] 连续填入 0。复写非零元素:cur = 3,将 arr[3] 的值 3 复制到 arr[4]。继续填充非零和零元素:cur = 2 和 cur = 1 分别填入 2 和两个 0。最终结果:通过逆序复写确保零元素不覆盖其他元素,得到 [1, 0, 0, 2, 3, 0, 0, 4]。 易错点提示
目标位置初始化:dest 从 -1 开始,以保证cur准确定位复写后数组最后一个元素在原来数组的位置。越界处理:若 dest 超出数组边界时,最后一个位置设为零,并调整 cur 和 dest。逆序复写逻辑:确保零元素复写两次、非零复写一次,保证整个过程的准确性。 代码复杂度
时间复杂度:O(n),只需遍历两次。空间复杂度:O(1),仅使用少量额外变量。 1.3 盛最多水的容器
1. 题目链接
11. 盛最多水的容器
2. 题目描述
给定一个长度为 n 的整数数组 height,有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i])。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
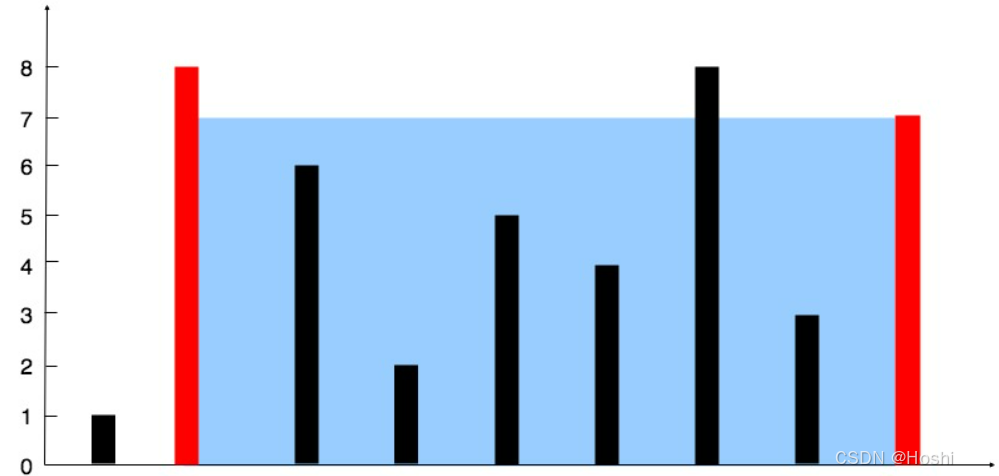
说明:你不能倾斜容器。
示例 1:
输入:[1,8,6,2,5,4,8,3,7]输出:49解释:数组中的垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在这个情况下,能够容纳水(表示为蓝色部分)的最大值是 49。 解法一(暴力求解)
算法思路:
枚举出所有可能构成的容器,找出其中容积最大的值。容器容积的计算方式: 设指针i 和 j 分别指向容器的最左端和最右端,此时容器的宽度为 j - i。由于容器的高度由两条边中较短的决定,因此容积的公式为:v = (j - i) * min(height[i], height[j])代码实现:
class Solution {public: int maxArea(vector<int>& height) { int n = height.size(); int ret = 0; // 两层 for 循环枚举出所有可能出现的情况 for (int i = 0; i < n; i++) { for (int j = i + 1; j < n; j++) { // 计算容积,找出最大的那一个 ret = max(ret, min(height[i], height[j]) * (j - i)); } } return ret; }};复杂度分析:
时间复杂度:O(n^2)。需要遍历所有的可能组合,计算每个组合的容积,因此时间复杂度为平方级别。空间复杂度:O(1)。只使用了常数个变量存储结果和中间值。 缺点:
该算法对大数据集会产生性能问题,会超时。因此需要寻找更高效的解法。解法二(对撞指针)
算法思路:
使用两个指针left 和 right 分别指向容器的左右两个端点。容器的初始状态为 left 在最左侧,right 在最右侧。容积公式:v = (right - left) * min(height[right], height[left])left++。因为固定左边界且继续移动右边界,只会使得容器宽度减小,而高度仍然由左边的短板决定,因此容积只能减小。同理,如果右边界小于左边界,则移动右边界 right--,以尝试找到更高的边界,从而可能获得更大的容积。 重复以上过程,直到 left 与 right 相遇,整个过程中不断更新最大容积的值。 代码实现:
class Solution {public: int maxArea(vector<int>& height) { int left = 0, right = height.size() - 1, ret = 0; while (left < right) { int v = min(height[left], height[right]) * (right - left); ret = max(ret, v); // 移动指针 if (height[left] < height[right]) { left++; } else { right--; } } return ret; }};复杂度分析:
时间复杂度:O(n)。只需要遍历整个数组一次,两个指针分别从头和尾相向而行。空间复杂度:O(1)。只使用了常数个变量存储结果和指针位置。 核心思想与证明:
双指针法的有效性:通过每次移动较短边界的方式,可以确保不会遗漏任何可能的最大容积的组合。因为容器的高度由两侧较短的一边决定,通过移动较短的那一边,我们尝试找到更高的边界,保持或增加容积。为什么移动短板?: 当左右边界不相等时,容器的高度取决于较短的一边。如果固定较短边界而移动较长边界,容器的高度不会增加,宽度还会减小,因此容积一定会减少。而如果移动较短的边,可能找到一个更高的边,从而在宽度减少的情况下保持或增加高度,从而有可能获得更大的容积。易错点提示
指针移动逻辑:
在指针移动过程中,不是随机移动,而是根据较短边界的高度决定移动哪个指针。目的是通过增加高度的可能性来找到更大的容积。边界条件的处理:
初始状态left = 0,right = height.size() - 1,要注意判断数组的长度不能为零,否则无法构成容器。 复杂度对比与结论
暴力求解法:时间复杂度为O(n^2),对于较大的输入会导致超时,适合小规模数据。对撞指针法:时间复杂度为 O(n),只需线性遍历,适合大规模输入,能够有效解决性能问题。 小结
这道题考察了如何通过合理的指针移动来减少不必要的计算,双指针法的精髓在于每次有目的地舍弃一些不可能产生最大值的组合,从而将时间复杂度降至线性。在实际解题时,双指针法是一种非常高效的解法,特别适用于涉及到对区间或边界的遍历优化问题。通过这两种方法的对比,我们可以看到,暴力法虽然简单,但在性能上存在很大的不足,而通过双指针策略,我们能够有效地减少重复计算,找到问题的最优解。
第二章:快慢指针
2.1 复写零
题目链接
202. 快乐数
题目描述
编写一个算法来判断一个数 n 是不是快乐数。
快乐数定义:
对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程,直到这个数变为1,或者进入无限循环但始终无法变为 1。如果这个过程结果为 1,那么这个数就是快乐数。如果 n 是快乐数就返回 true;否则返回 false。 示例 1:
输入:n = 19输出:true解释: 19 -> 1^2 + 9^2 = 8282 -> 8^2 + 2^2 = 6868 -> 6^2 + 8^2 = 100100 -> 1^2 + 0^2 + 0^2 = 1 示例 2:
输入:n = 2输出:false解释: 2 -> 4 -> 16 -> 37 -> 58 -> 89 -> 145 -> 42 -> 20 -> 4 -> 16出现了重复的数字,因此进入了无限循环,不是快乐数。 题目分析
为了方便叙述,将“对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和”这一操作记为 x 操作。
题目告诉我们,当我们不断重复 x 操作 时,计算一定会进入“死循环”,而“死循环”的方式有两种:
1,即 1 -> 1 -> 1 -> 1...,这是“快乐数”。情况二:在某个历史数值中循环,始终变不到 1。 由于上述两种情况只会出现一种,因此,只要我们能确定循环是在“情况一”还是“情况二”,就能判断该数是否是快乐数。
简单证明:
变化值范围:经过一次变化后的最大值为9^2 * 10 = 810(即最大的情况是 9999999999(实际上这道题没有这么大),由鸽巢原理,这个值最终的范围在 [1, 810] 之间)。循环保证:根据“鸽巢原理”,一个数变化 811 次之后,必然会形成一个循环。因此,变化的过程最终会进入一个圈里,可以使用快慢指针来判断是否进入循环。 解法(快慢指针)
算法思路:
根据题目分析,我们可以知道,当重复执行 x 操作 时,数值会陷入某种“循环”之中。而快慢指针有一个特性,就是在一个环中,快指针总是会追上慢指针,也就是说它们总会相遇在某个位置上。
1,则这个数是快乐数;如果相遇的位置不是 1,则这个数不是快乐数。 补充知识:如何求一个数 n 每个位置上的数字的平方和:
n 每一位的数字提取出来,使用以下步骤: 提取个位:int t = n % 10去掉个位:n /= 10重复上面的步骤,直到 n 的值为 0。 在提取每一位时,用一个变量 sum 记录平方和:sum += t * t C++代码实现
以下是 C++ 的代码实现,使用快慢指针来解决该问题:
class Solution {public: int bitSum(int n) { // 返回 n 的每一位上的平方和 int sum = 0; while (n) { int t = n % 10; // 提取个位 sum += t * t; // 累加平方和 n /= 10; // 去掉个位 } return sum; } bool isHappy(int n) { int slow = n, fast = bitSum(n); while (slow != fast) { // 使用快慢指针,直到二者相遇 slow = bitSum(slow); // 慢指针每次走一步 fast = bitSum(bitSum(fast)); // 快指针每次走两步 } return slow == 1; // 判断相遇点是否为 1 }};代码解析
bitSum 函数: 用于求一个数 n 的每位数字平方和。通过循环不断提取个位,计算平方和,直到 n 为 0。 isHappy 函数: 初始化两个指针 slow 和 fast,分别为 n 和 bitSum(n)。使用 快慢指针 的方式来进行循环,slow 每次只走一步,而 fast 每次走两步。如果 slow 和 fast 相遇,退出循环。最后判断是否相遇在 1 上,若是则返回 true,表示为快乐数,否则返回 false。 易错点提示
快慢指针相遇判断:
需要注意的是,当slow 和 fast 相遇时,如果该值为 1,则为快乐数;如果不是 1,则表明进入了其他循环。 平方和计算函数的实现:
在实现bitSum 函数时,需要注意提取个位后立即对其平方,并累加到总和中,最后在循环结束后返回结果。 复杂度分析
时间复杂度:O(log n)。在快慢指针法中,求平方和的时间复杂度为对数级。空间复杂度:O(1)。没有使用额外的数据结构,只使用了固定数量的变量。 写在最后
在这篇文章中,我们从基础开始,深入探讨了双指针方法在解决常见数组问题中的魔力。双指针法的魅力在于其精妙的指针移动方式,使得看似复杂的问题变得简单而高效。通过实例与代码实现,我们详细讲解了对撞指针和双指针的使用,帮助大家掌握这一关键的算法技巧。
但算法学习之路还在继续。随着基础知识的夯实,我们将在下一篇博客中,进一步探讨双指针的进阶用法,包括复杂数据结构中的应用以及更多高效算法的实现。接下来,欢迎大家阅读【C++ 双指针详解:进阶题解与思维分析】,一起深入学习双指针在更复杂场景中的应用。
以上就是关于【优选算法篇】双指针的优雅舞步:C++ 算法世界的浪漫探索的内容啦,各位大佬有什么问题欢迎在评论区指正,或者私信我也是可以的啦,您的支持是我创作的最大动力!❤️
