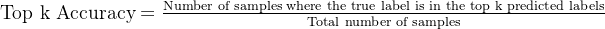在数据科学和机器学习中,评估模型的性能通常需要使用各种指标。这些指标可以帮助我们理解模型的预测能力和误差大小。
1. Mean Squared Error (MSE)
均方误差
MSE 是预测值与真实值之间差的平方的平均值,用于衡量模型的预测误差。MSE 越小,模型的预测效果越好。
公式: 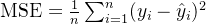
其中:
n是样本数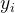 是真实值
是真实值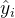 是预测值
是预测值 2. Mean Absolute Error (MAE)
平均绝对误差
MAE 是预测值与真实值之间绝对差的平均值。它比 MSE 更容易解释,因为它直接反映了预测值与真实值之间的平均差距。
公式: 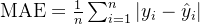
3. Root Mean Squared Error (RMSE)
均方根误差
RMSE 是 MSE 的平方根,用于保持单位与原始数据一致。它可以更加直观地反映预测误差的大小。
公式: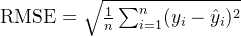
4. Mean Absolute Percentage Error (MAPE)
平均绝对百分比误差
MAPE 是预测误差的绝对值与真实值的百分比的平均值,常用于衡量预测相对误差的大小。
公式: 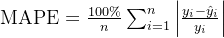
5. Mean Absolute Relative Error (MARE)
平均绝对相对误差
MARE 是预测误差与真实值的比值的平均值。与 MAPE 类似,MARE 也衡量相对误差,但通常不乘以 100%。
公式: 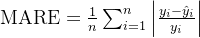
6. Symmetric Mean Absolute Percentage Error (SMAPE)
对称平均绝对百分比误差
SMAPE 是一种修改的 MAPE,避免了真实值为零的问题。它考虑了预测值和真实值的对称差异。
公式: 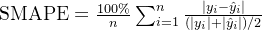
7. Accuracy (ACC)
准确率
在分类任务中,准确率是预测正确的样本数与总样本数之比。对于回归任务,通常用类似准确度的指标衡量,如 R^2。
公式: 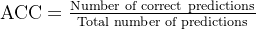
8. Top k Accuracy (TOP k)
前 k 准确率
Top k 准确率是指预测的前 k 个类别中包含正确类别的比例,常用于多分类任务。
公式: