目录
1 什么是堆1.1 堆的逻辑结构和物理结构1.2 堆的访问1.3 堆为什么物理结构上要用数组?1.4 堆数据上的特点 2 堆的实现2.1 堆类型定义2.2 需要实现的接口2.3 初始化堆2.4 销毁堆2.5 堆判空2.6 交换函数2.7 向上调整(小堆)2.8 向下调整(小堆)2.9 堆插入2.10 堆删除2.11 //堆顶 3 完整代码3.1 heap.h3.2 heap.c
1 什么是堆
简单来说堆是二叉树的一种表示方式,它在逻辑上就是一颗完全二叉树,它在物理上却是一个数组,这么说可能有点抽象,我们原来学习的栈,队列,或者说顺序表,链表等等,他们的逻辑结构和物理结构是相同或者相似的,就会比较好理解一些,而在堆这里物理结构和逻辑结构截然不同,理解相对就会比较抽象一些,我们接着看1.1 堆的逻辑结构和物理结构
逻辑结构即我们想象的结构,就比方说我们早上在图书馆排队的时候,放个包在图书馆门口,人可能都不见了,这个时候我们逻辑上认为我们在排队,但物理上我们同学就可能在吃早饭上厕所啥的逻辑上我们想象这个数组是一个二叉树,并且像二叉树一样访问子节点或者父节点 比方说我给出以下数组,它在逻辑上是这样表示的(当然哈,指针其实是不存在的,只是逻辑上我们看作其是父子关系):
1.2 堆的访问
既然堆是一颗货真价实的二叉树,可我们怎么像二叉树一样,通过父/子节点访问子/父节点呢?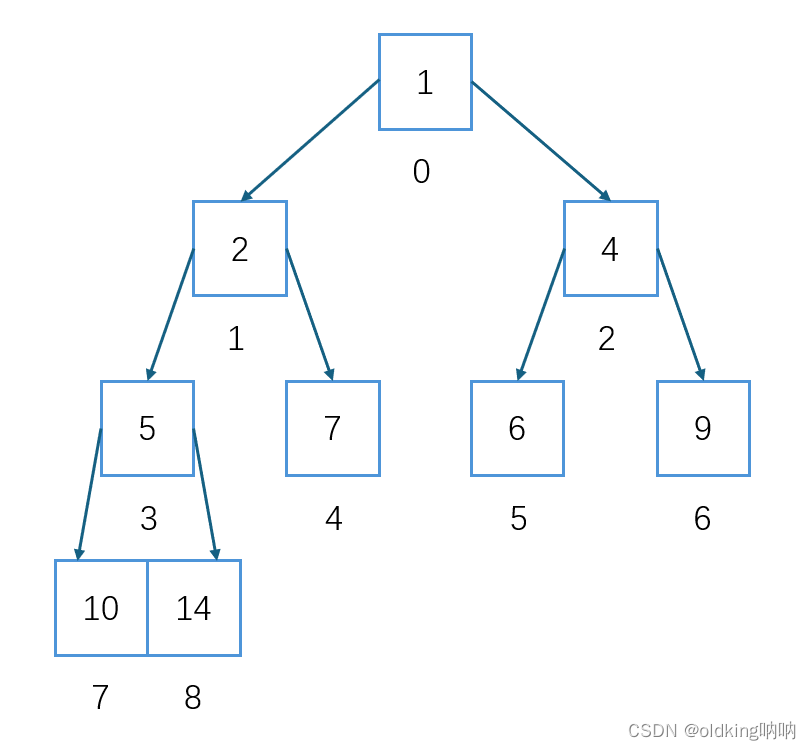
父节点的下标 * 2 + 1 或 父节点的下标 * 2 + 2 即可 即 7 或 8 通过子节点访问父节点 我们假设子节点的下标为7,我们想访问它的父节点,只需要把 (子节点的下标 - 1) / 2 即可 即 3我们假设子节点的下表为8,我们想访问它的父节点,依旧只需要把 (子节点的下标 - 1) / 2 即可 依旧是 3 1.3 堆为什么物理结构上要用数组?
事实上学习堆是为了学习堆排序打基础,在堆排序中,有时候需要频繁交换头尾节点,如果用数组,找节点就会方便很多,交换函数也很好写,效率会更高,用链表要不断去遍历,或者专门写个尾指针妥协,很没必要其次,如果我们用链式存储的话,访问子/父节点需要定义3个指针,需要多开辟很多空间堆一定是完全二叉树,用数组存放会很方便,其中不会有空节点,所有数据存储都是连续的1.4 堆数据上的特点
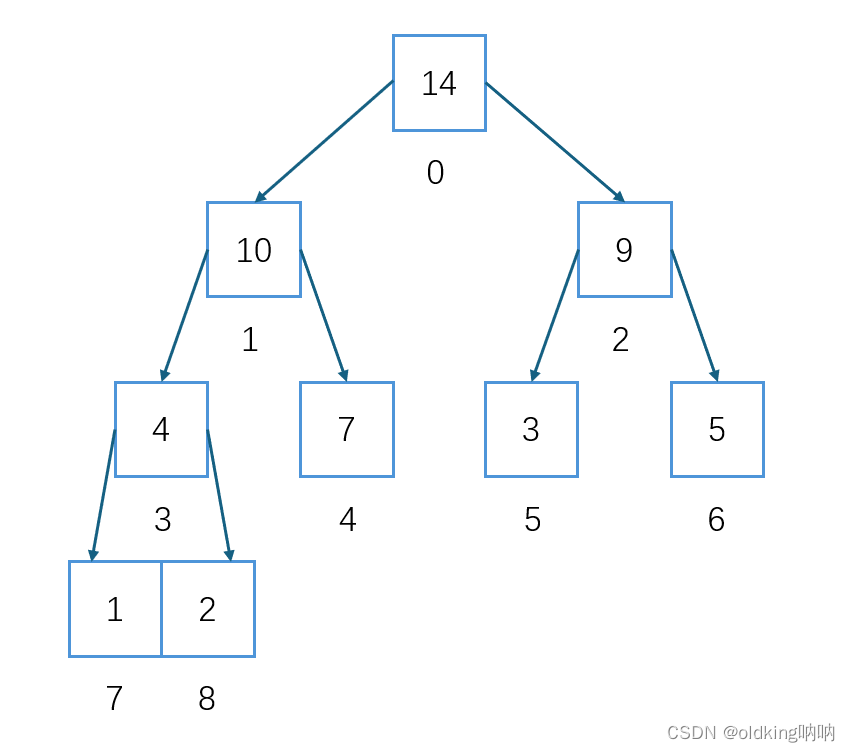
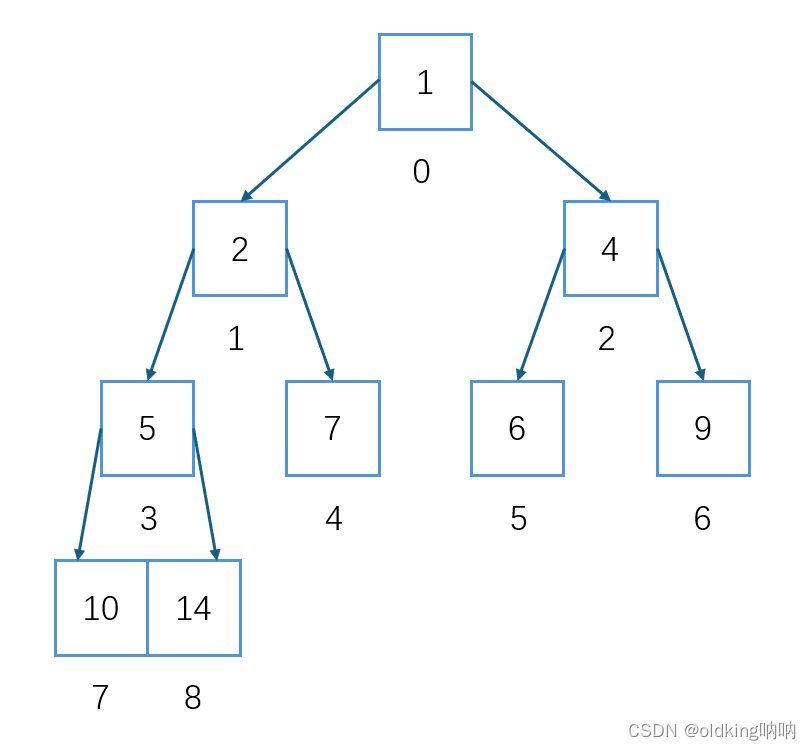
堆必须要始终满足满足:父节点值比子节点小或者父节点始终比子节点大我们称父节点值始终比子节点小的堆为小堆/小根堆我们称父节点值始终比子节点大的堆为大堆/大根堆例如:
1.大堆:
2.小堆:
2 堆的实现
2.1 堆类型定义
//堆在物理上是一个数组,我们直接按数组的定义方式就行//类型定义typedef int HPDataType;typedef struct Heap {HPDataType* data;int size;int capa;}Heap;2.2 需要实现的接口
//交换函数void Swap(HPDataType* x, HPDataType* y);//向上调整(小堆)void AdjustUp(HPDataType* data, int child);//向下调整(小堆)void AdjustDown(HPDataType* data, int size, int father);//初始化堆void HPInit(Heap* php);//销毁堆void HPDestroy(Heap* php);//堆插入void HPPush(Heap* php, HPDataType x);//堆删除void HPPop(Heap* php);//堆顶HPDataType HPTop(Heap* php);//堆判空bool HPEmpty(Heap* php);2.3 初始化堆
//像顺序表一样初始化就行//初始化堆void HPInit(HP* php){assert(php);php->a = (HPdatatype*)calloc(4, sizeof(HPdatatype));if (php->a == NULL){perror("HPInit::calloc fail");exit(1);}php->capa = 4;php->size = 0;}2.4 销毁堆
//同样,像顺序表一样销毁就行//销毁堆void HPdestory(HP* php){assert(php);free(php->a);php->a = NULL;php->capa = 0;php->size = 0;}2.5 堆判空
//堆判空bool HPEmpty(HP* php){assert(php); //判空return php->size == 0; //size是0就返回true}2.6 交换函数
//只是完成数据在空间上的交换//交换函数void Swap(HPdatatype* x, HPdatatype* y){HPdatatype tmp = *x;*x = *y;*y = tmp;}2.7 向上调整(小堆)
注意这里是重点向上调整会在很多地方用到,基本思想就是让本应该在上面的节点往上挪//向上调整(小堆)void AdjustUp(HPdatatype* a, int child){assert(a);//判空int father = (child - 1) / 2;//推算出父节点的位置while (father < child && a[father] > a[child]) //只要子节点比父节点还小,就让子节点和父节点交换{ //重复此步骤直到子节点大于父节点或者子节点和自己比较Swap(&a[child], &a[father]); child = father;father = (child - 1) / 2;}}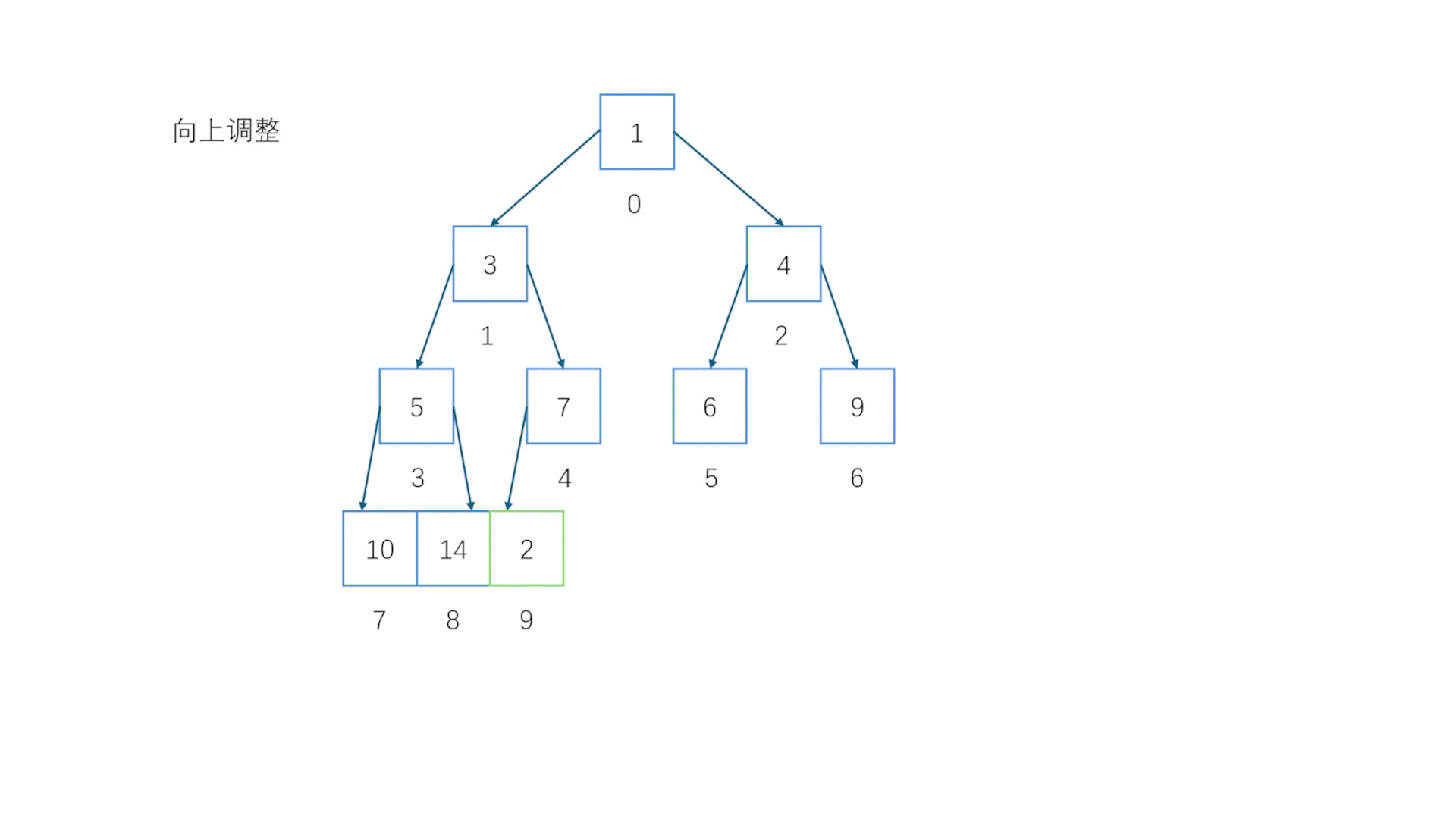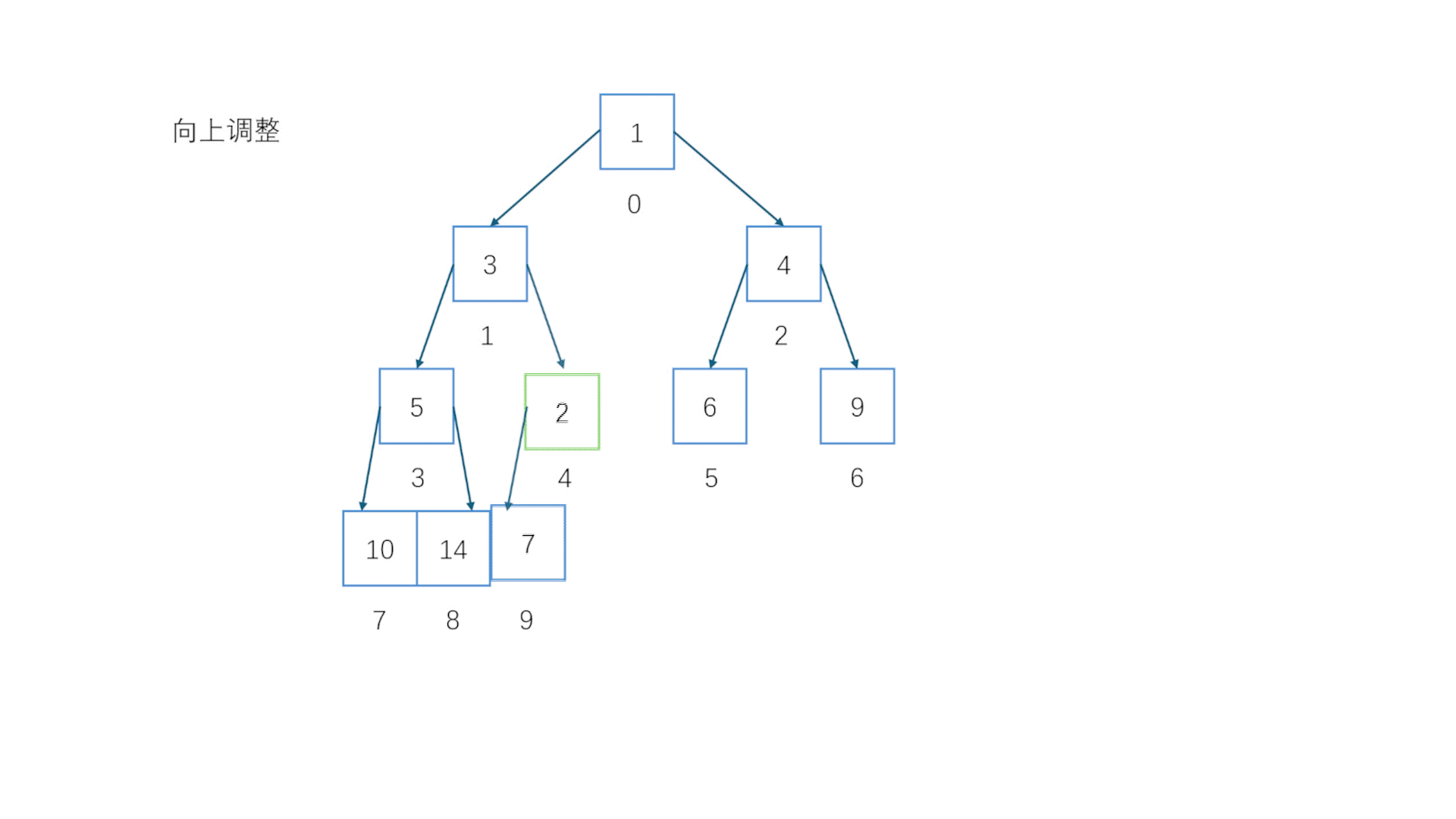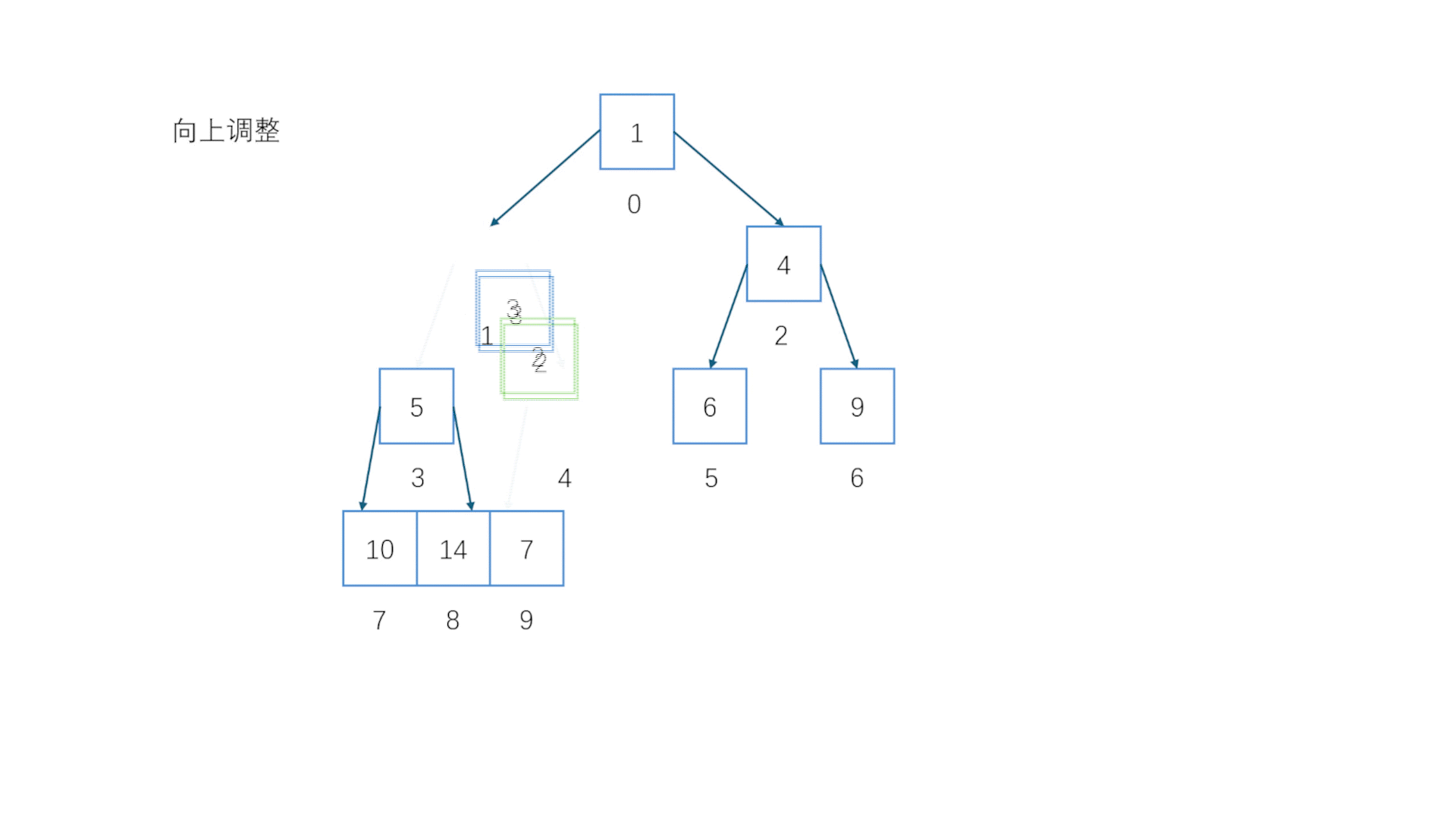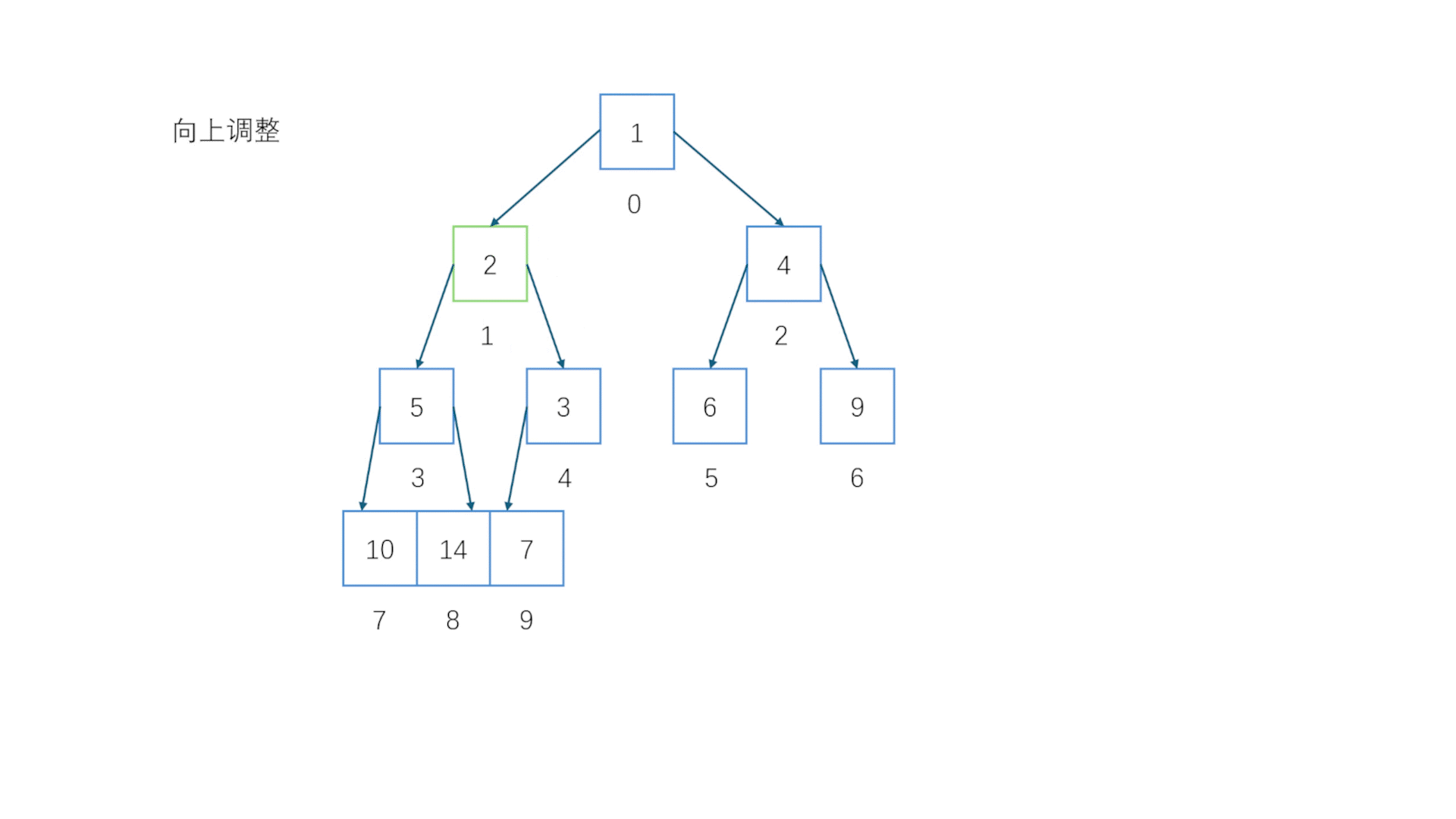
2.8 向下调整(小堆)
注意这里是重点向下调整同样会在很多地方用到//向下调整(小堆)void AdjustDown(HPdatatype* a, int size, int father){assert(a);//判空int child = (father * 2) + 1; //先假设比较小的是左子节点if (child + 1 < size && a[child] > a[child + 1]) //如果右子节点比左子节点大,注意要判断一下子节点是否会超范围{child++; //把child改成右子节点}while (child < size && a[father] > a[child] ) //如果父节点一直比子节点大就不断交换下移{ //直到子节点超出size范围或者父节点比子节点小就停下Swap(&a[father], &a[child]); //交换father = child; //重新找到父节点(交换后的父节点应该是原来的子节点的位置)child = (father * 2) + 1; //重新定位子节点if (child + 1 < size && a[child] > a[child + 1]) //如法炮制{child++;}}}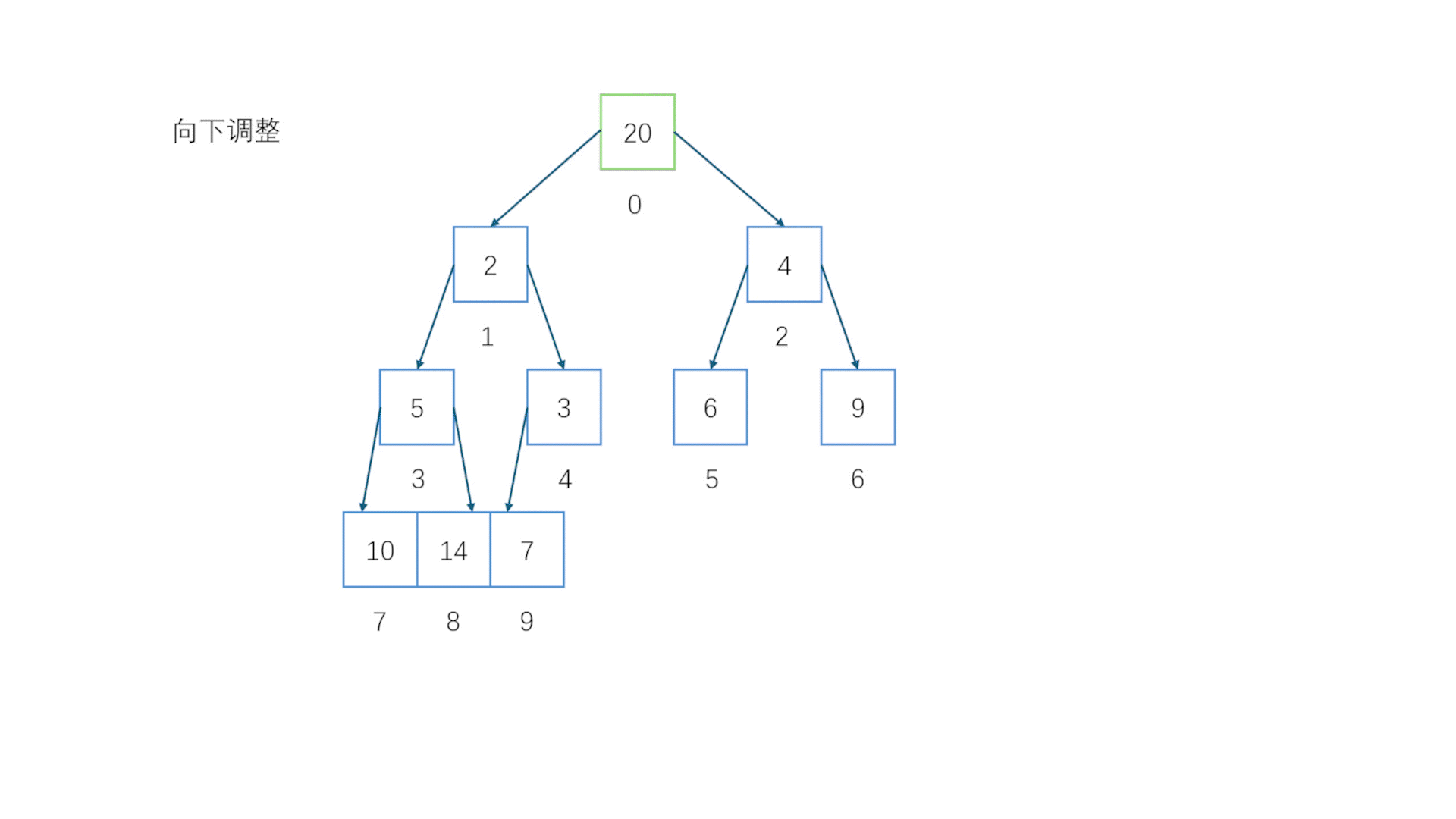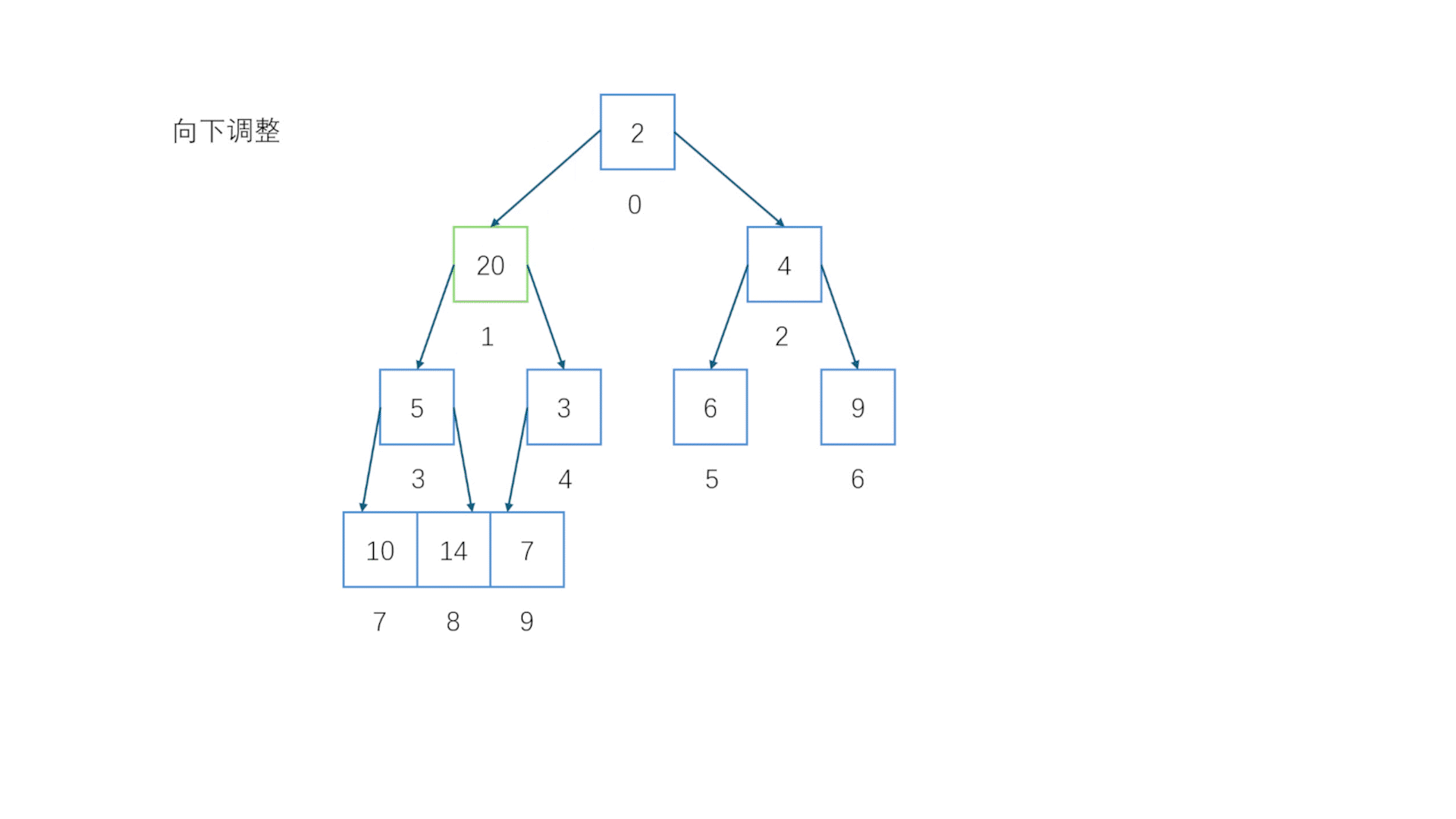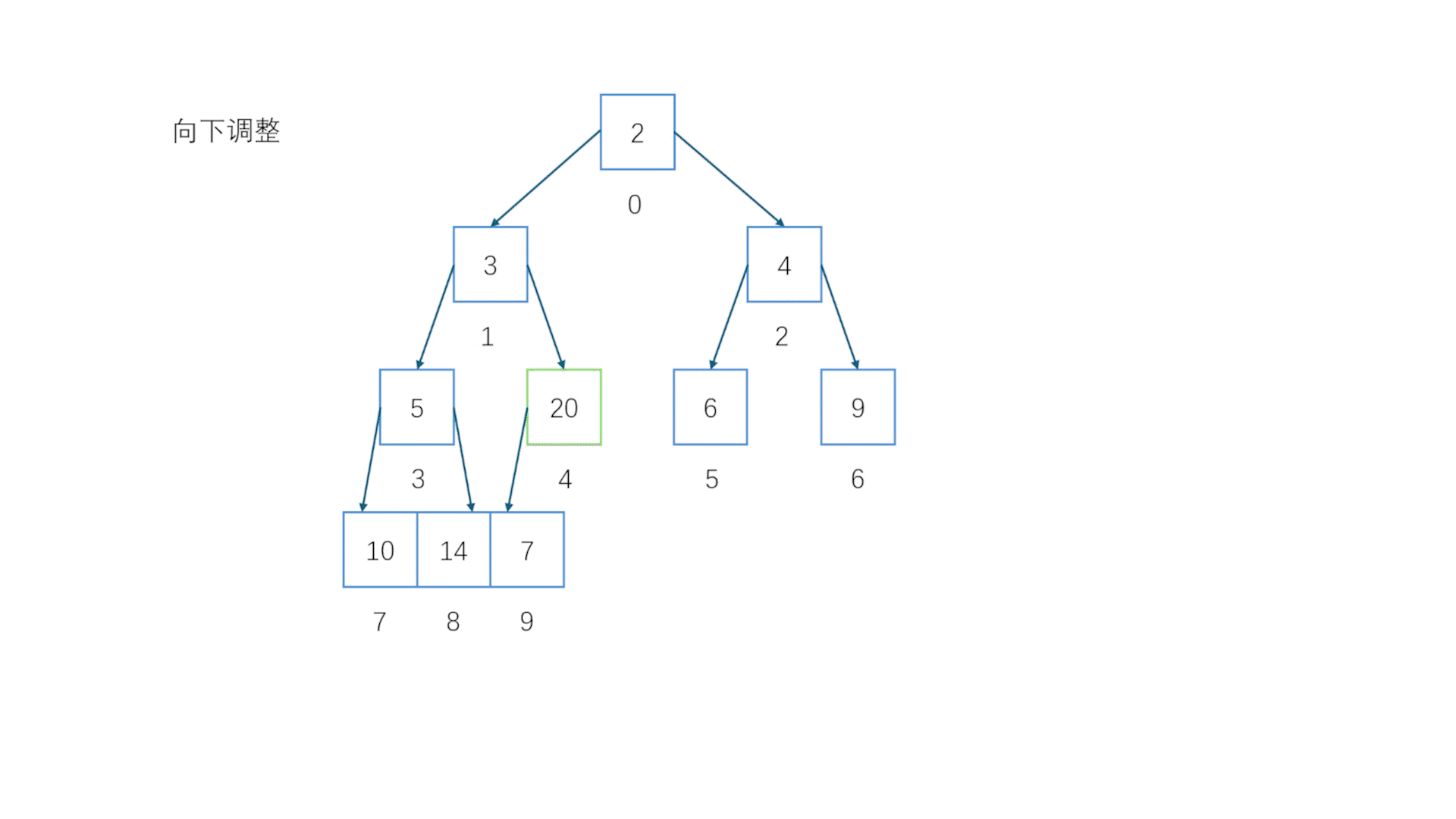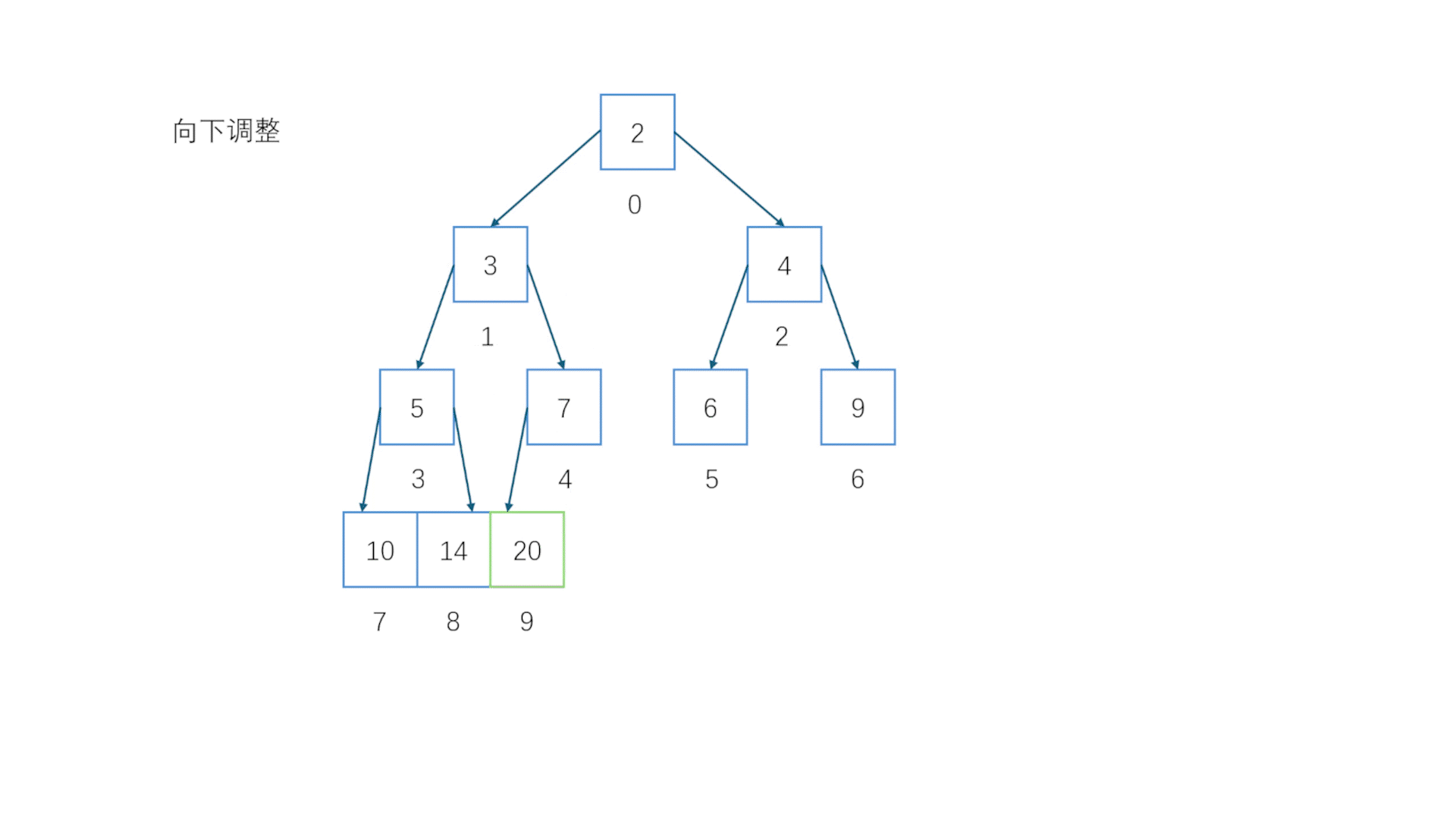
2.9 堆插入
堆插入一般插入到末尾,因为末尾很空,啥也没有,比较好插入,插在其他地方还得先挪动才可以插入//堆插入void HPPush(HP* php, HPdatatype x){assert(php); //判空//堆扩容,这里像数组一样扩容就行if (php->capa == php->size){HPdatatype* tmp = (HPdatatype*)realloc(php->a, 2 * php->size * sizeof(HPdatatype));if (tmp == NULL){perror("HPPush::realloc fail");exit(1);}php->a = tmp;php->capa *= 2;}php->a[php->size] = x; //将要插入的数据放到堆低AdjustUp(php->a, php->size); //通过向上调整找到这个数据本应该在的位置php->size++; //别忘了让size++}2.10 堆删除
堆删除一般删除堆顶的数据,但不能简单地把堆顶置为空,而是要和末尾数据交换,再一点点下调//堆删除void HPPop(HP* php){assert(php); //判空if (!HPEmpty(php)) //如果堆不是空堆{Swap(&php->a[0], &php->a[php->size - 1]); //交换堆顶和末尾的数据AdjustDown(php->a, php->size - 1, 0); //将堆顶的数据向下挪到合适的位置php->size--; //别忘了size--}}2.11 //堆顶
//取堆顶HPdatatype HPTop(HP* php){assert(php); //判空return HPEmpty(php) ? -1 : php->a[0]; //返回堆顶数据}完整代码在最下面哦
佬!都看到这了,如果觉得有帮助的话一定要点赞啊佬 >v< !!!
放个卡密在这,感谢各位能看到这儿啦!

3 完整代码
3.1 heap.h
#pragma once//头文件声明#include <stdio.h>#include <stdlib.h>#include <assert.h>#include <stdbool.h>#include <string.h>//类型定义typedef int HPdatatype;typedef struct Heap{HPdatatype* a;int size;int capa;}HP;//函数申明//交换函数void Swap(HPDataType* x, HPDataType* y);//向上调整(小堆)void AdjustUp(HPDataType* data, int child);//向下调整(小堆)void AdjustDown(HPDataType* data, int size, int father);//初始化堆void HPInit(Heap* php);//销毁堆void HPDestroy(Heap* php);//堆插入void HPPush(Heap* php, HPDataType x);//堆删除void HPPop(Heap* php);//堆顶HPDataType HPTop(Heap* php);//堆判空bool HPEmpty(Heap* php);3.2 heap.c
#include "heap.h"//初始化堆void HPInit(HP* php){assert(php);php->a = (HPdatatype*)calloc(4, sizeof(HPdatatype));if (php->a == NULL){perror("HPInit::calloc fail");exit(1);}php->capa = 4;php->size = 0;}//销毁堆void HPdestory(HP* php){assert(php);free(php->a);php->a = NULL;php->capa = 0;php->size = 0;}//堆判空bool HPEmpty(HP* php){assert(php);return php->size == 0;}//取堆顶HPdatatype HPTop(HP* php){assert(php);return HPEmpty(php) ? -1 : php->a[0];}//交换void Swap(HPdatatype* x, HPdatatype* y){HPdatatype tmp = *x;*x = *y;*y = tmp;}//向上调整(小堆)void AdjustUp(HPdatatype* a, int child){assert(a);int father = (child - 1) / 2;while (father < child && a[father] > a[child]){Swap(&a[child], &a[father]);child = father;father = (child - 1) / 2;}}//堆插入void HPPush(HP* php, HPdatatype x){assert(php);//堆扩容if (php->capa == php->size){HPdatatype* tmp = (HPdatatype*)realloc(php->a, 2 * php->size * sizeof(HPdatatype));if (tmp == NULL){perror("HPPush::realloc fail");exit(1);}php->a = tmp;php->capa *= 2;}php->a[php->size] = x;AdjustUp(php->a, php->size);php->size++;}//向下调整(小堆)void AdjustDown(HPdatatype* a, int size, int father){assert(a);int child = (father * 2) + 1;if (child + 1 < size && a[child] > a[child + 1]){child++;}while (child < size && a[father] > a[child] ){Swap(&a[father], &a[child]);father = child;child = (father * 2) + 1;if (child + 1 < size && a[child] > a[child + 1]){child++;}}}//堆删除void HPPop(HP* php){assert(php);if (!HPEmpty(php)){Swap(&php->a[0], &php->a[php->size - 1]);AdjustDown(php->a, php->size - 1, 0);php->size--;}}