目录
- 1:何为梯度下降
- 1.1 简单描述
- 1.2 直观描述
- 1.3 假设
- 2.符号说明
- 3.具体步骤
- 4.简单的证明
- 5.优化
- 5.1 模型的缺点
- 5.1.1效率
- 5.1.2 准确度
- 5.1.3 具有迷惑性的平原
- 5.1.4 局部最优解
- 5.2 优化算法
- 5.2.1 Adagrad
- 5.2.2 SGDM
- 5.2.3 Adam
- 参考文献
1:何为梯度下降
1.1 简单描述
通过迭代的思想解决函数求最值的问题(下文会以求最小值为例)
1.2 直观描述

如上图,从一个点出发,不断的向能使函数值减小最快的方向移动点,直到找到最小值
1.3 假设
假设存在一个可微分函数 f ( x , y ) f(x,y) f(x,y),当然不仅仅局限于二次函数
2.符号说明
| 符号 | 意义 |
|---|---|
| η \eta η | 学习指数 |
| g i g_i gi | d f d x i \frac{d f}{d x_i} dxidf |
| λ \lambda λ | 惯性系数 |
| β 1 \beta_1 β1 | 0.9 |
| β 2 \beta_2 β2 | 0.999 |
| ϵ \epsilon ϵ | 1 0 − 8 10^{-8} 10−8 |
3.具体步骤
一:随机取点
随机在函数上取一点
(
x
0
,
y
0
)
(x_0,y_0)
(x0,y0)
二:反复迭代
x
1
=
x
0
−
η
∗
∂
f
∂
x
∣
x
=
x
0
,
y
=
y
0
x_1=x_0-\eta* \left. \frac{\partial f}{\partial x} \right|_{x=x_0,y=y_0}
x1=x0−η∗∂x∂f∣∣∣x=x0,y=y0
y
1
=
y
0
−
η
∗
∂
f
∂
y
∣
x
=
x
0
,
y
=
y
0
y_1=y_0-\eta* \left. \frac{\partial f}{\partial y} \right|_{x=x_0,y=y_0}
y1=y0−η∗∂y∂f∣∣∣x=x0,y=y0
x
2
=
x
1
−
η
∗
∂
f
∂
x
∣
x
=
x
1
,
y
=
y
1
x_2=x_1-\eta* \left. \frac{\partial f}{\partial x} \right|_{x=x_1,y=y_1}
x2=x1−η∗∂x∂f∣∣∣x=x1,y=y1
y
2
=
y
1
−
η
∗
∂
f
∂
y
∣
x
=
x
1
,
y
=
y
1
y_2=y_1-\eta* \left. \frac{\partial f}{\partial y} \right|_{x=x_1,y=y_1}
y2=y1−η∗∂y∂f∣∣∣x=x1,y=y1
…
三:结束迭代
结束迭代一般有2种条件,根据不同情况而定
1:规定一定的迭代次数,达到一定次数后结束迭代
2:定义一个合理的阈值,当连续多次迭代所得结果之间的差值小于该阈值时,迭代结束
(对于为什么要多次迭代,会在后面说明)
4.简单的证明
假设 f ( x , y ) f(x,y) f(x,y)在点 ( x k , y k ) (x_k,y_k) (xk,yk)处 n n n阶可导则 f ( x , y ) f(x,y) f(x,y)在 ( x k , y k ) (x_k,y_k) (xk,yk)的一个领域内有
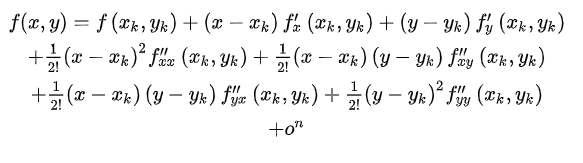
也就是泰勒公式,如果我们只考虑
(
x
k
,
y
k
)
(x_k,y_k)
(xk,yk)附加一个很小的领域,也就是能满足
x
−
x
k
x-x_k
x−xk和
y
−
y
k
y-y_k
y−yk的值很小,那么可以不考虑泰勒展开中二次及二次以后的项,也就是只保留
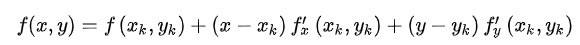
我们的目标是在这个很小的领域内找到使函数值减小最快的
(
x
,
y
)
(x,y)
(x,y)的移动方向,那么我们可以将问题简化为在
(
x
−
x
k
)
2
+
(
y
−
y
k
)
2
≤
r
2
(x-x_k)^2+(y-y_k)^2\leq r^2
(x−xk)2+(y−yk)2≤r2(其中r很小)中研究
(
x
−
x
k
)
∗
a
+
(
y
−
y
k
)
∗
b
(x-x_k)*a+(y-y_k)*b
(x−xk)∗a+(y−yk)∗b随
(
x
,
y
)
(x,y)
(x,y)的变化规律,其中a,b分表代表式中2个偏微分。其中
(
a
,
b
)
(a,b)
(a,b)是以
(
x
k
,
y
k
)
(x_k,y_k)
(xk,yk)为起点的一个向量,
(
x
−
x
k
,
y
−
y
k
)
(x-x_k,y-y_k)
(x−xk,y−yk)也是以
(
x
k
,
y
k
)
(x_k,y_k)
(xk,yk)为起点的一个向量,而我们要求的正好是这2个向量的乘积
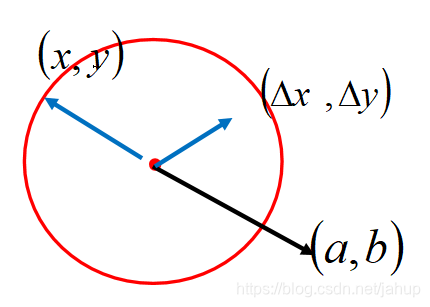
那么可得,当
(
x
,
y
)
(x,y)
(x,y)沿
(
a
,
b
)
(a,b)
(a,b)相反方向移动时
(
x
−
x
k
)
∗
a
+
(
y
−
y
k
)
∗
b
(x-x_k)*a+(y-y_k)*b
(x−xk)∗a+(y−yk)∗b减小的最快,也就是
f
(
x
,
y
)
f(x,y)
f(x,y)减小的最快。那么每次沿该方向迭代
(
x
,
y
)
(x,y)
(x,y)就能很快的找到此迭代所能找到的最小值。
x
1
=
x
0
−
η
∗
∂
f
∂
x
∣
x
=
x
0
,
y
=
y
0
x_1=x_0-\eta* \left. \frac{\partial f}{\partial x} \right|_{x=x_0,y=y_0}
x1=x0−η∗∂x∂f∣∣∣x=x0,y=y0
y
1
=
y
0
−
η
∗
∂
f
∂
y
∣
x
=
x
0
,
y
=
y
0
y_1=y_0-\eta* \left. \frac{\partial f}{\partial y} \right|_{x=x_0,y=y_0}
y1=y0−η∗∂y∂f∣∣∣x=x0,y=y0
上式中引入
η
\eta
η,是因为2个偏微分的值我们无法预测,如果过大会使得此次迭代2个坐标的位置改变较大,但证明成立的条件是在一个很小的领域内变动,故此处需要引入
η
\eta
η
5.优化

5.1 模型的缺点
5.1.1效率
x
1
=
x
0
−
η
∗
∂
f
∂
x
∣
x
=
x
0
,
y
=
y
0
x_1=x_0-\eta* \left. \frac{\partial f}{\partial x} \right|_{x=x_0,y=y_0}
x1=x0−η∗∂x∂f∣∣∣x=x0,y=y0
y
1
=
y
0
−
η
∗
∂
f
∂
y
∣
x
=
x
0
,
y
=
y
0
y_1=y_0-\eta* \left. \frac{\partial f}{\partial y} \right|_{x=x_0,y=y_0}
y1=y0−η∗∂y∂f∣∣∣x=x0,y=y0
从式中可以看出
η
\eta
η的大小会直接影响点的偏移量,如果偏移量过小,需要大量的迭代次数才能得到理想结果,也就是上图蓝色箭头表示的情况
5.1.2 准确度
当 η \eta η取的偏大时,点的偏移量会增大,而当我们很接近最低点时,过大的 η \eta η可能会导致直接跳过了最低点,也就是上图绿色和黄色的情况
5.1.3 具有迷惑性的平原
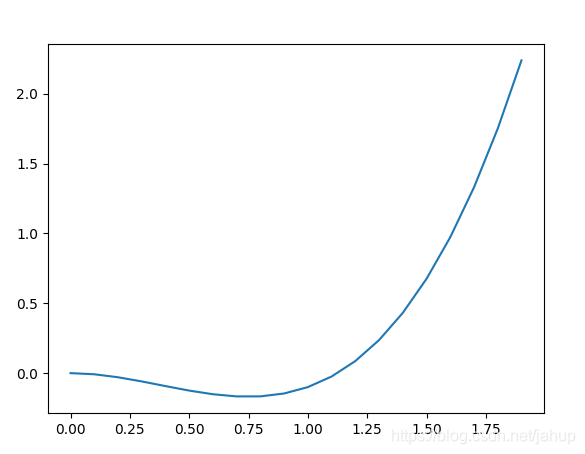
上文提过结束迭代的条件如下

如上图函数所示,函数的左端是一段斜率极小的很平滑的曲线,下文简称为平原,当我们通过迭代使得点进入平原时,因为5.1.2所提及的原因,我们无法将
η
\eta
η设的太大,那么进入平原后,点的偏移量会大大减小,使得迭代的次数快速增加,对于结束迭代的条件1,我们可以通过牺牲效率提高迭代次数来避免最后结果落在平原.但对于条件2,因为平原偏移量可能非常的小,导致相邻2次迭代结果的差可能低于阈值,所以我们通过多次迭代的差来判断是否结束迭代,但这种方法只对较小的平原有用,对于较大的平原结果任然有可能落在平原.而且无论是对于条件1还是条件2在这种情况下效率都极低。
5.1.4 局部最优解
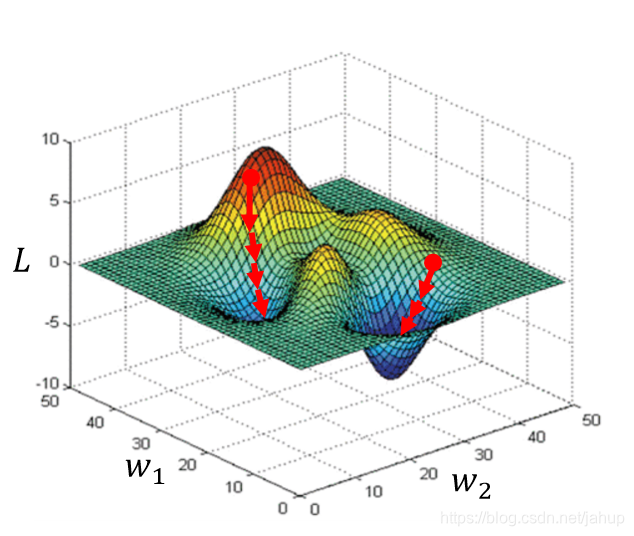
上图很形象的说明了,迭代的起始点不同,可能会导致迭代的结果为局部最优解
5.2 优化算法
对于上面的缺点,研究人员找出了一些优化方法,其能在一定程度上减弱这些缺点的影响
5.2.1 Adagrad
该模型对迭代式进行了一定程度上的改变(为了方便描述,这里以一元函数为例)
x
1
=
x
0
−
η
(
∑
k
=
0
0
(
g
k
)
2
)
∗
g
0
x_1=x_0- \frac{\eta}{\sqrt(\sum_{k=0}^0 (g_k)^2)}*g_0
x1=x0−(
∑k=00(gk)2)η∗g0
x
2
=
x
1
−
η
(
∑
k
=
0
1
(
g
k
)
2
)
∗
g
1
x_2=x_1- \frac{\eta}{\sqrt(\sum_{k=0}^1 (g_k)^2)}*g_1
x2=x1−(
∑k=01(gk)2)η∗g1
x
3
=
x
2
−
η
(
∑
k
=
0
2
(
g
k
)
2
)
∗
g
2
x_3=x_2- \frac{\eta}{\sqrt(\sum_{k=0}^2 (g_k)^2)}*g_2
x3=x2−(
∑k=02(gk)2)η∗g2
…
x
i
=
x
i
−
1
−
η
(
∑
k
=
0
i
−
1
(
g
k
)
2
)
∗
g
i
−
1
x_i=x_{i-1}- \frac{\eta}{\sqrt(\sum_{k=0}^{i-1} (g_k)^2)}*g_{i-1}
xi=xi−1−(
∑k=0i−1(gk)2)η∗gi−1
从式子可以看出 η ( ∑ k = 0 i ( g k ) 2 ) \frac{\eta}{\sqrt(\sum_{k=0}^i (g_k)^2)} ( ∑k=0i(gk)2)η的值随着迭代的不断增加而减小,也就是在迭代开始时点的偏移量较大,迭代次数越多,越接近最低点时,偏移量逐渐减小,这样既提高了效率,也能保持一定的准确度
5.2.2 SGDM
该模型也是对迭代式进行了改变
v
0
=
0
v_0=0
v0=0
v
1
=
λ
∗
v
0
−
η
∗
g
0
v_1=\lambda*v_0-\eta*g_0
v1=λ∗v0−η∗g0
x
1
=
x
0
+
v
1
x_1=x_0+v_1
x1=x0+v1_
v
2
=
λ
∗
v
1
−
η
∗
g
1
v_2=\lambda*v_1-\eta*g_1
v2=λ∗v1−η∗g1
x
2
=
x
1
+
v
2
x_2=x_1+v_2
x2=x1+v2
…
v
i
=
λ
∗
v
i
−
1
−
η
∗
g
i
−
1
v_i=\lambda*v_{i-1}-\eta*g_{i-1}
vi=λ∗vi−1−η∗gi−1
x
i
=
x
i
−
1
+
v
i
x_i=x_{i-1}+v_i
xi=xi−1+vi
对于该模型,每一次计算此次移动的偏移量时,都会考虑到此前产生的偏移量,下文我们称为惯性,这点有点类似物理学中的惯性,此时的运动状态不仅仅受此时的受力情况影响,还受之前的运动状态影响,引入这一点,使得模型与真实的情况更加类似。
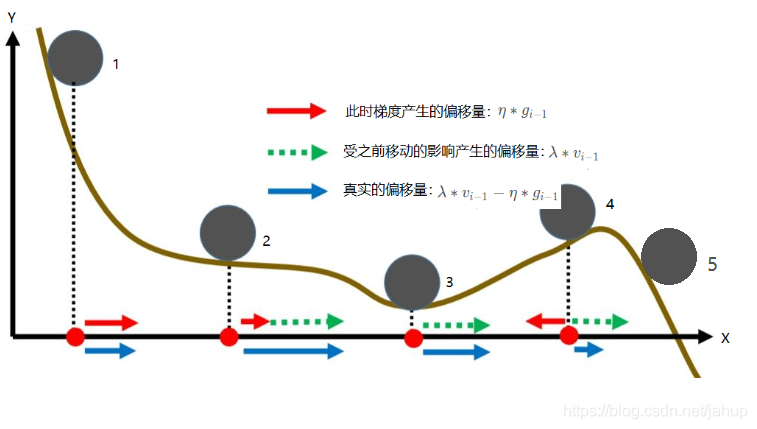
如上图所示,引入惯性,可以在一定程度上解决因为平原导致的效率低下的问题,如球2所示,也能在一定程度上解决局部最优解的问题,如球3到球4到球5
5.2.3 Adam
该模型也是对迭代式进行了改变
m
0
=
g
0
m_0=g_0
m0=g0
v
0
=
g
0
2
v_0=g_0^2
v0=g02
m
0
′
=
m
0
1
−
β
1
0
m_0'= \frac{m_0}{1-\beta_1^0}
m0′=1−β10m0
v
0
′
=
v
0
1
−
β
2
0
v_0'= \frac{v_0}{1-\beta_2^0}
v0′=1−β20v0
x
1
=
x
0
−
η
(
x
0
′
)
+
ϵ
∗
m
0
′
x_1=x_0-\frac{\eta}{\sqrt(x_0')+\epsilon}*m_0'
x1=x0−(
x0′)+ϵη∗m0′
m
1
=
β
1
∗
m
0
+
(
1
−
β
1
)
∗
g
1
m_1=\beta_1*m_0+(1-\beta_1)*g_1
m1=β1∗m0+(1−β1)∗g1
v
1
=
β
2
∗
v
0
+
(
1
−
β
2
)
∗
g
1
2
v_1=\beta_2*v_0+(1-\beta_2)*g_1^2
v1=β2∗v0+(1−β2)∗g12
m
1
′
=
m
1
1
−
β
1
1
m_1'= \frac{m_1}{1-\beta_1^1}
m1′=1−β11m1
v
1
′
=
v
1
1
−
β
2
1
v_1'= \frac{v_1}{1-\beta_2^1}
v1′=1−β21v1
x
2
=
x
1
−
η
(
v
1
′
)
+
ϵ
∗
m
1
′
x_2=x_1-\frac{\eta}{\sqrt(v_1')+\epsilon}*m_1'
x2=x1−(
v1′)+ϵη∗m1′
…
m
i
=
β
1
∗
m
i
−
1
+
(
1
−
β
1
)
∗
g
i
m_i=\beta_1*m_{i-1}+(1-\beta_1)*g_{i}
mi=β1∗mi−1+(1−β1)∗gi
v
i
=
β
2
∗
v
i
−
1
+
(
1
−
β
2
)
∗
g
i
2
v_i=\beta_2*v_{i-1}+(1-\beta_2)*g_i^2
vi=β2∗vi−1+(1−β2)∗gi2
m
i
′
=
m
i
1
−
β
1
i
m_i'= \frac{m_i}{1-\beta_1^i}
mi′=1−β1imi
v
i
′
=
v
i
1
−
β
2
i
v_i'= \frac{v_i}{1-\beta_2^i}
vi′=1−β2ivi
x
i
+
1
=
x
i
−
η
(
v
i
′
)
+
ϵ
∗
m
i
′
x_{i+1}=x_i-\frac{\eta}{\sqrt(v_i')+\epsilon}*m_i'
xi+1=xi−(
vi′)+ϵη∗mi′
其中参数的值在符号说明给出

Adam可以说是目前,同类算法中综合表现最出色的算法,被广泛的应用于翻译等诸多场合
参考文献
https://blog.csdn.net/hyg1985/article/details/42556847
https://www.zhihu.com/question/305638940
https://blog.csdn.net/luoxuexiong/article/details/90412213
https://blog.csdn.net/zb1165048017/article/details/78392623?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.baidujs&dist_request_id=&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.baidujs
https://zh.wikipedia.org/zh-hans/%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D%E6%B3%95
https://baike.baidu.com/item/%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D/4864937?fr=aladdin
https://www.youtube.com/watch?v=Syom0iwanHo

--某科学的超电磁炮