做每件事之前都心存诚意, 就会事半功倍.
目录
前言1. 根据二叉树创建字符串2. 二叉树的层序遍历Ⅰ3. 二叉树的层序遍历Ⅱ4. 二叉树的最近公共祖先5. 二叉搜索树与双向链表6. 根据一棵树的前序遍历与中序遍历构造二叉树7. 根据一棵树的中序遍历与后序遍历构造二叉树8. 二叉树的前序遍历,非递归迭代实现9. 二叉树中序遍历 ,非递归迭代实现10. 二叉树的后序遍历 ,非递归迭代实现
前言
一些面试中可能会遇到的二叉树的进阶题目, 这些题目我们也需要进行掌握.
博客主页: 酷酷学!!!
更多好文, 持续关注
正文开始
1. 根据二叉树创建字符串
题目链接: 根据二叉树创建字符串
题目描述:
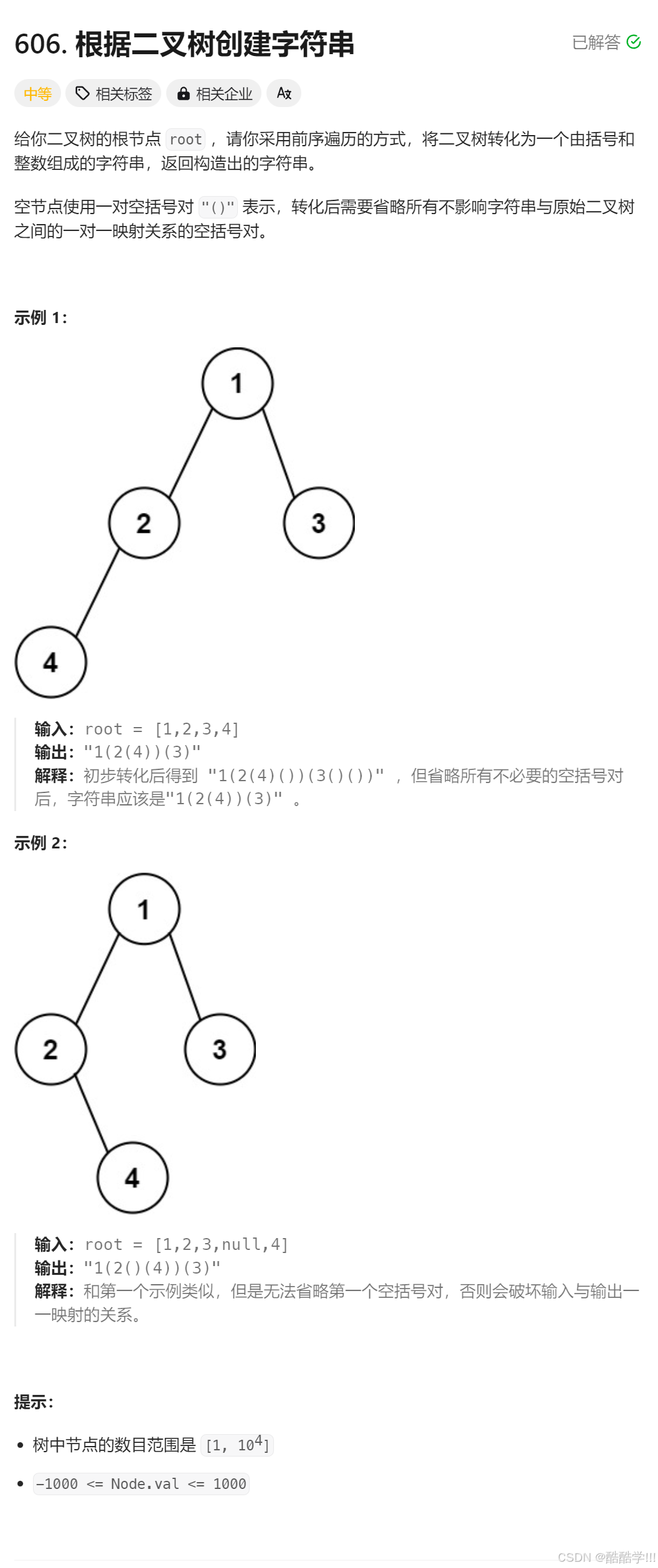
题目思路:
根据前序遍历创建二叉树, 再递归子树之前需要加括号, 但是题目要求省略不必要的括号, 通过观察可发现
左右子树都为空, 省略括号右子树为空,省略括号左为空, 右不为空, 不能省略括号每次递归之前加上条件即可, 不要忘记将整型转化为字符串, 字符串不能直接相加整型数据
题目代码:
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */class Solution {public: string tree2str(TreeNode* root) { string str; if(root == nullptr) return str; str+= to_string(root->val);//两个都为空就省略括号 if(root->left || root->right) { str+='('; str+=tree2str(root->left); str+=')'; }//右子树存在则都要括号 if(root->right) { str+='('; str+=tree2str(root->right); str+=')'; } return str; }};2. 二叉树的层序遍历Ⅰ
题目链接: 二叉树的层序遍历Ⅰ
题目描述:
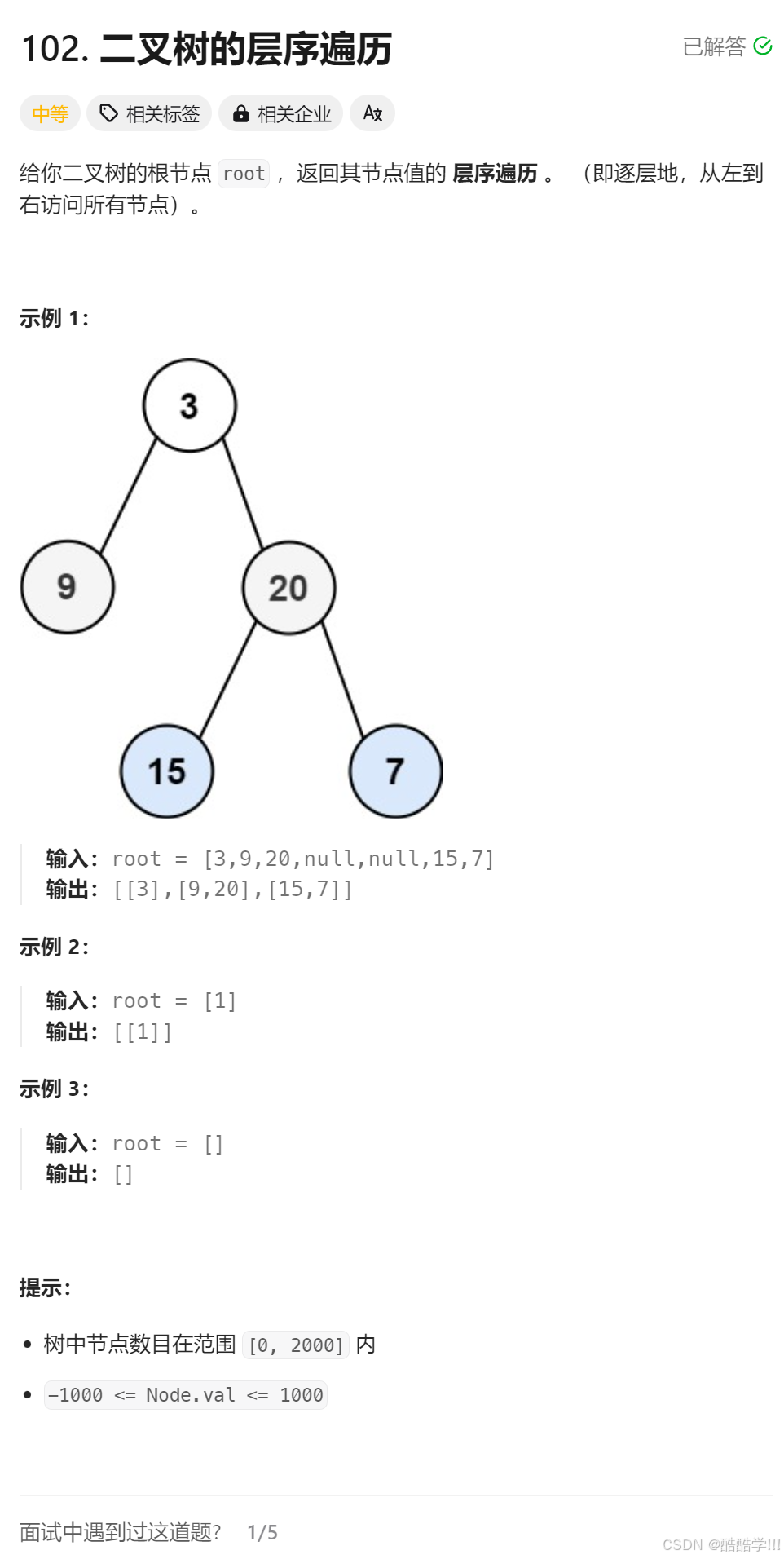
题目思路:
我们在层序遍历过程中,增加一个levelSize,记录每层的数据个数,树不为空的情况下,第1层levelSize=1,循环控制,第1层出完了,第2层就都进队列了,队列中size就是第2层的数据个数。以此内推,假设levelSize为第n层的数据个数,因为层序遍历思想为当前层结点出队列,带入下一层结点(也就是子结点),循环控制第n层数据出完了,那么第n+1结点都进队列了,队列size,就是下⼀层的levelSize。
题目代码:
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */class Solution {public: vector<vector<int>> levelOrder(TreeNode* root) { vector<vector<int>> vv; queue<TreeNode*> q; int levelsize = 1; if(root == nullptr) return vv; q.push(root); while(levelsize) { vector<int> v; while(levelsize--) { TreeNode* front = q.front(); v.push_back(front->val); if(front->left) q.push(front->left); if(front->right) q.push(front->right); q.pop(); } vv.push_back(v); levelsize = q.size(); } return vv; }};3. 二叉树的层序遍历Ⅱ
题目链接: 二叉树的层序遍历Ⅱ
题目描述:
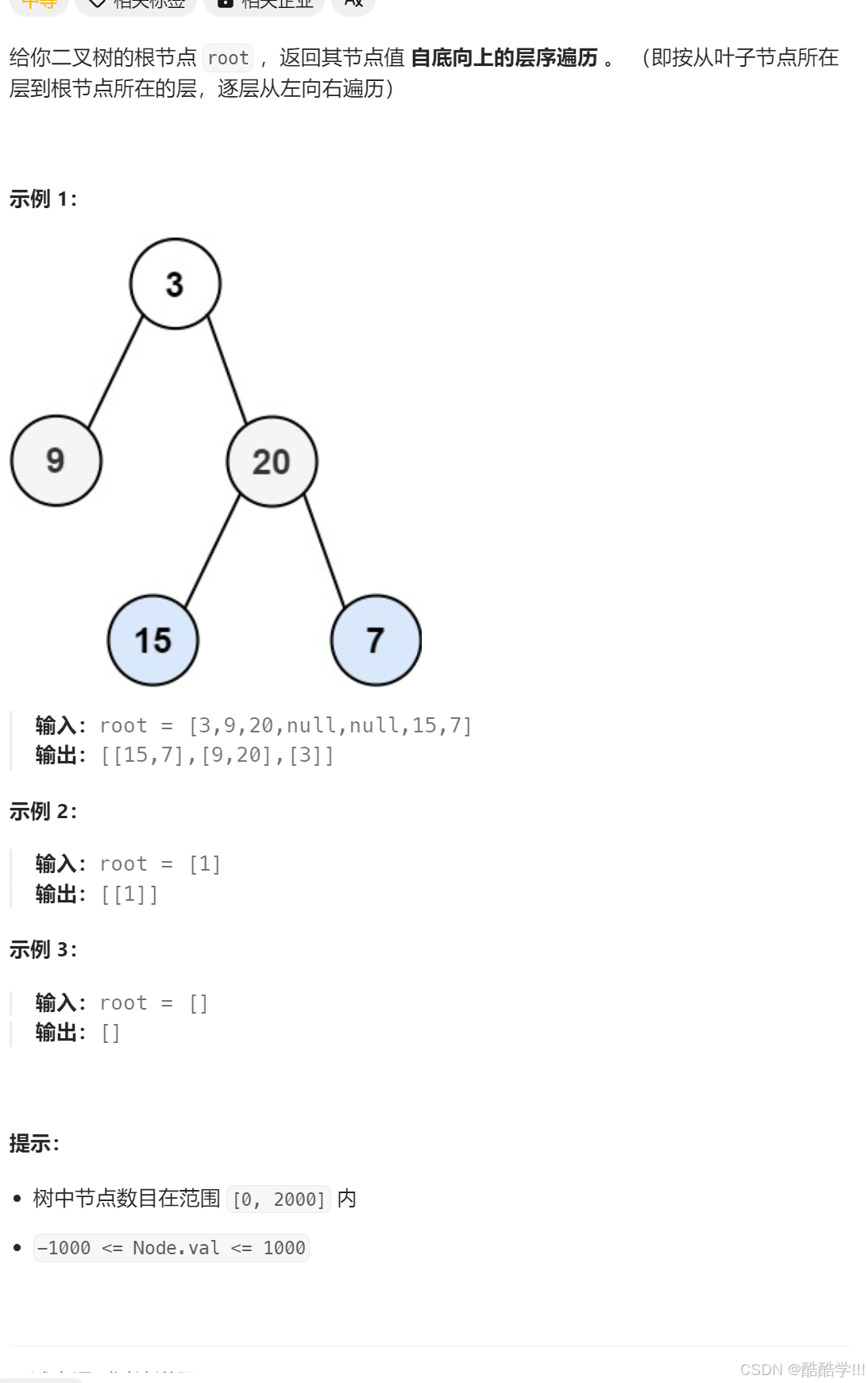
题目思路:
107的第二个题目,思路跟上题102⼀样,只⼆维数组逆置⼀下就可以得到结果。
题目代码:
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */class Solution {public: vector<vector<int>> levelOrderBottom(TreeNode* root) { vector<vector<int>> vv; int levelsize = 0; queue<TreeNode*> q; if(root) { q.push(root); levelsize = 1; } while(levelsize>0) { vector<int> v; while(levelsize--) { TreeNode* front = q.front(); q.pop(); v.push_back(front->val); if(front->left) q.push(front->left); if(front->right) q.push(front->right); } levelsize = q.size(); vv.push_back(v); } reverse(vv.begin(),vv.end()); return vv; }};4. 二叉树的最近公共祖先
题目链接: 二叉树的最近公共祖先
题目描述:
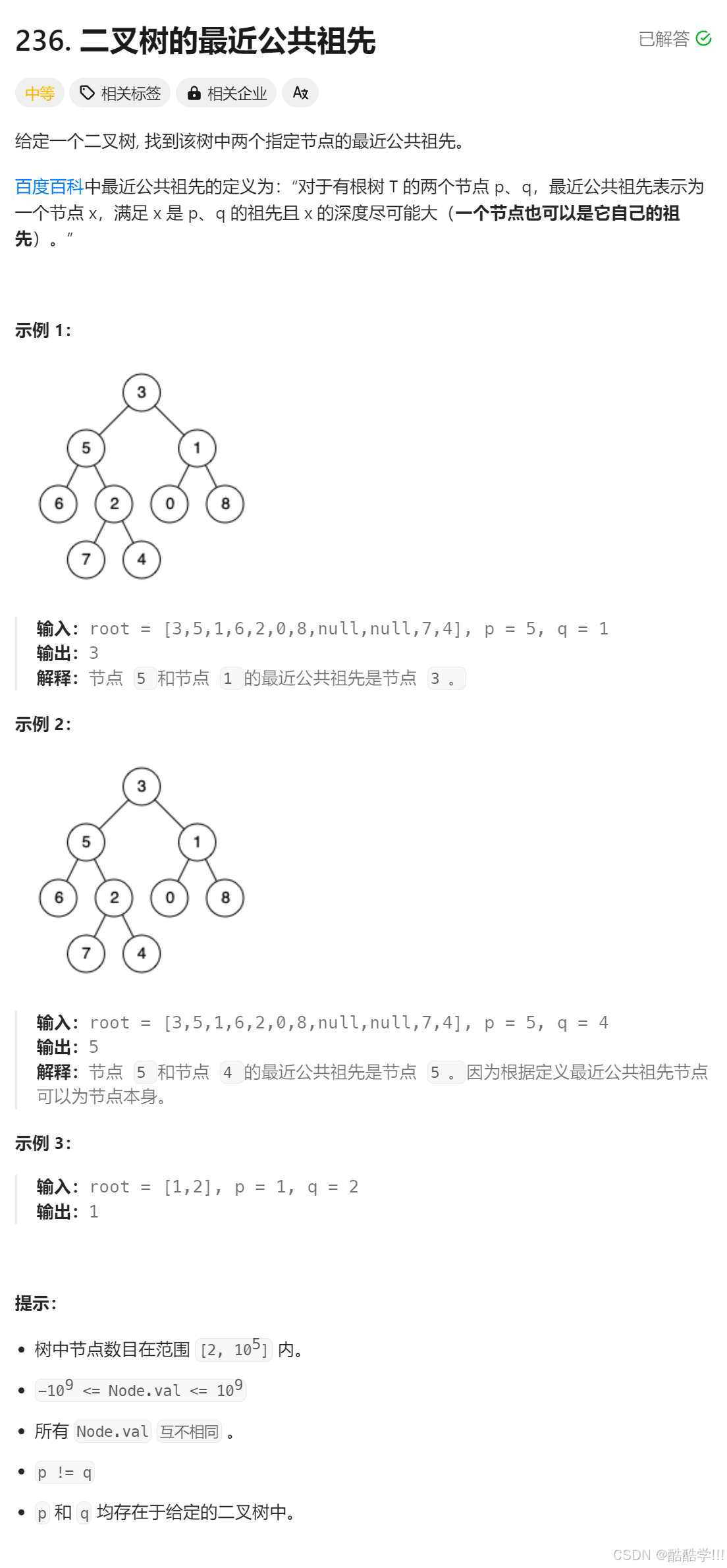
题目思路:
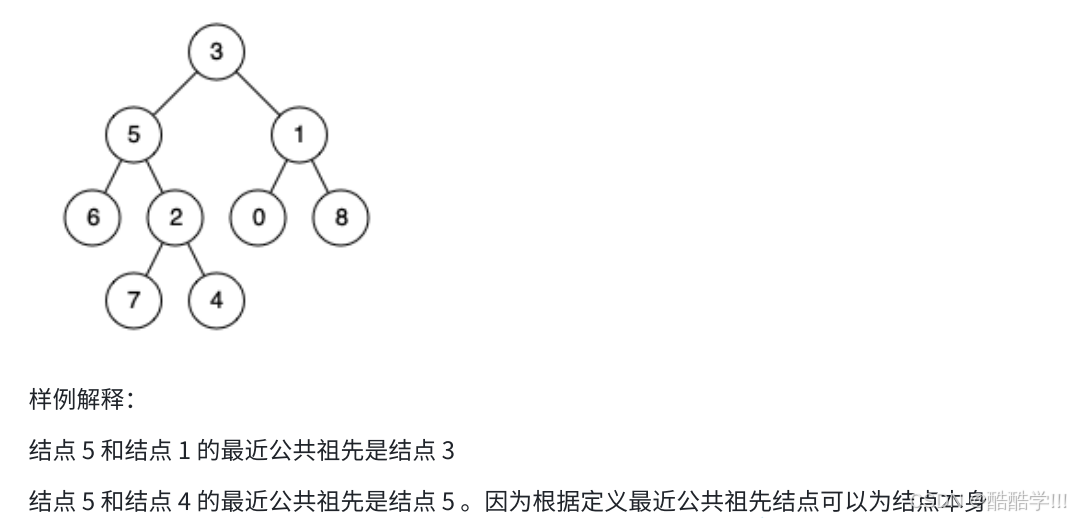
思路1:仔细观察⼀下,两个结点,最近公共祖先的特征就是⼀个结点在最近公共祖先的左边,⼀个结点在最近公共祖先的右边。⽐如6和4的公共祖先有5和3,但是只有最近公共祖先5满⾜6在左边,4在右边。
思路2:如果能求出两个结点到根的路径,那么就可以转换为链表相交问题。如:6到根3的路径为6->5->3,4到根3的路径为4->2->5->3,那么看做两个链表找交点,交点5就是最近公共祖先。
思路二时间复杂度更好一点,但是空间复杂度大一点
题目代码:
思路一:
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */class Solution {public: bool IsInTree(TreeNode* t,TreeNode* x) { if(t == nullptr) return false; return t == x || IsInTree(t->left,x) || IsInTree(t->right,x); } TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { if(root == nullptr) return nullptr; if(root == p || root == q) return root; //自此开始要么都在左,要么都在右 bool pInleft = IsInTree(root->left,p); bool pInright = !pInleft; bool qInleft = IsInTree(root->left,q); bool qInright = !qInleft; if((qInleft&&pInright) || (qInright&&pInleft)) return root; else if(pInleft && qInleft) return lowestCommonAncestor(root->left,p,q); else return lowestCommonAncestor(root->right,p,q); }};思路二:
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */class Solution {public: bool ancestor(TreeNode* root,TreeNode* node,stack<TreeNode*>& s) { if(root == nullptr) return false; s.push(root); if(root == node) return true; if(ancestor(root->left,node,s)) return true; if(ancestor(root->right,node,s)) return true; s.pop(); return false; } TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { stack<TreeNode*> pstack; stack<TreeNode*> qstack; ancestor(root,p,pstack); ancestor(root,q,qstack); while(pstack.size()>qstack.size()) { pstack.pop(); } while(qstack.size()>pstack.size()) { qstack.pop(); } while(qstack.top()!=pstack.top()) { pstack.pop(); qstack.pop(); } return qstack.top(); }};5. 二叉搜索树与双向链表
题目链接: 二叉搜索树与双向链表
题目描述:

题目思路:
搜索⼆叉树⾛中序是有序的,本题⽬要求原地修改,也就是不能创建新的结点。
思路1:中序遍历搜索⼆叉树,遍历顺序是有序的,将⼆叉树的结点指针放到⼀个vector中,再把前后结点的链接关系进⾏修改。这个思路最简单,但是需要消耗O(N)的空间复杂度。
思路2:依旧中序遍历搜索⼆叉树,遍历顺序是有序的,遍历过程中修改左指针为前驱和右指针为后继指针。记录⼀个cur和prev,cur为当前中序遍历到的结点,prev为上⼀个中序遍历的结点,cur->left指向prev,cur->right⽆法指向中序下⼀个,因为不知道中序下⼀个是谁,但是prev->right指向cur;也就是说每个结点的左是在中遍历到当前结点时修改指向前驱的,但是当前结点的右,是在遍历到下⼀个结点时,修改指向后继的。
代码如下:
/*struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;TreeNode(int x) :val(x), left(NULL), right(NULL) {}};*/class Solution {public:void InOrderConvert(TreeNode* cur,TreeNode*& prev){if(cur==nullptr) return;InOrderConvert(cur->left,prev);cur->left = prev;if(prev)prev->right = cur;prev = cur;InOrderConvert(cur->right,prev);} TreeNode* Convert(TreeNode* pRootOfTree) { if(pRootOfTree==nullptr) return nullptr;TreeNode* prev = nullptr;InOrderConvert(pRootOfTree,prev);TreeNode* head = pRootOfTree;while(head->left){head = head->left;}return head; }};6. 根据一棵树的前序遍历与中序遍历构造二叉树
题目链接: 根据一棵树的前序遍历与中序遍历构造二叉树
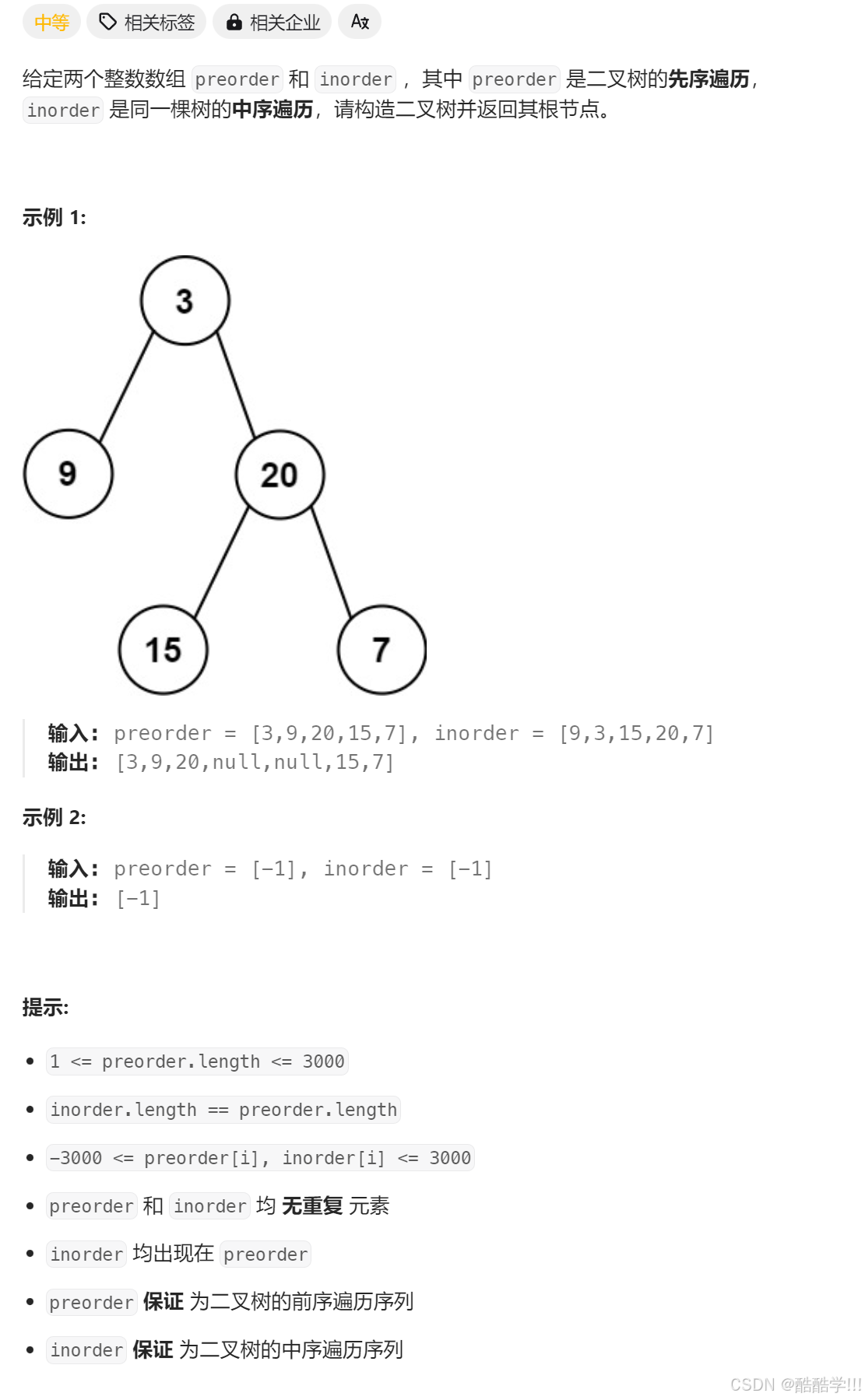
题目描述:
题目思路:
前序的⽅式构建树,前序确定当前构建树的根,根分割中序的左⼦树和右⼦树,再分别递归构建左⼦树和右⼦树。
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */class Solution {public: TreeNode* build(vector<int>& preorder,vector<int> inorder,int& prei,int inbegin,int inend) { if(inbegin>inend) return nullptr; //前序确定根 TreeNode* root = new TreeNode(preorder[prei]); //中序分割左右子树 int rooti = inbegin; while(rooti <= inend) { if(preorder[prei] == inorder[rooti]) break; else rooti++; } prei++; root->left = build(preorder,inorder,prei,inbegin,rooti-1); root->right = build(preorder,inorder,prei,rooti+1,inend); return root; } TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) { int i = 0; return build(preorder,inorder,i,0,inorder.size()-1); }};7. 根据一棵树的中序遍历与后序遍历构造二叉树
题目链接: 根据一棵树的中序遍历与后序遍历构造二叉树
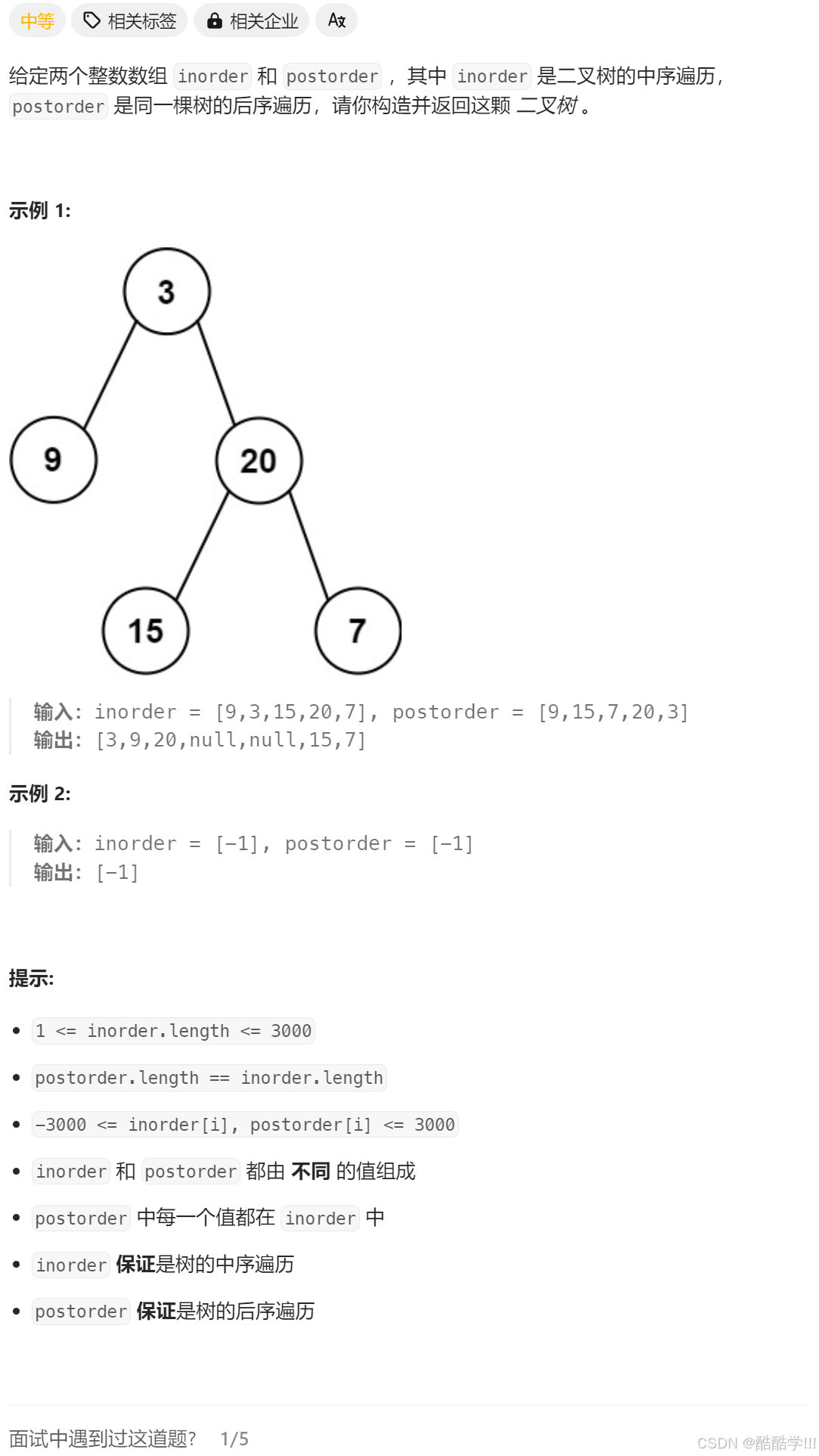
题目描述:
题目思路:
此题跟第六题差不多, 区别在于后续来确定根, 与上题相反, 且后续遍历的顺序是 左 右 根, 所以第二次取到是右子树的根, 故创建完根之后, 先创建右子树, 再创建根
题目代码:
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */class Solution {public: TreeNode* build(vector<int>& inorder, vector<int>& postorder,int& post,int inbegin,int inend) { if(inbegin>inend) return nullptr; TreeNode* newnode = new TreeNode(postorder[post]); int rooti = inbegin; while(rooti<=inend) { if(postorder[post] == inorder[rooti]) break; else rooti++; } post--; newnode->right = build(inorder,postorder,post,rooti+1,inend); newnode->left = build(inorder,postorder,post,inbegin,rooti-1); return newnode; } TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) { int post = postorder.size()-1; return build(inorder,postorder,post,0,inorder.size()-1); }};8. 二叉树的前序遍历,非递归迭代实现
题目链接: 二叉树的前序遍历
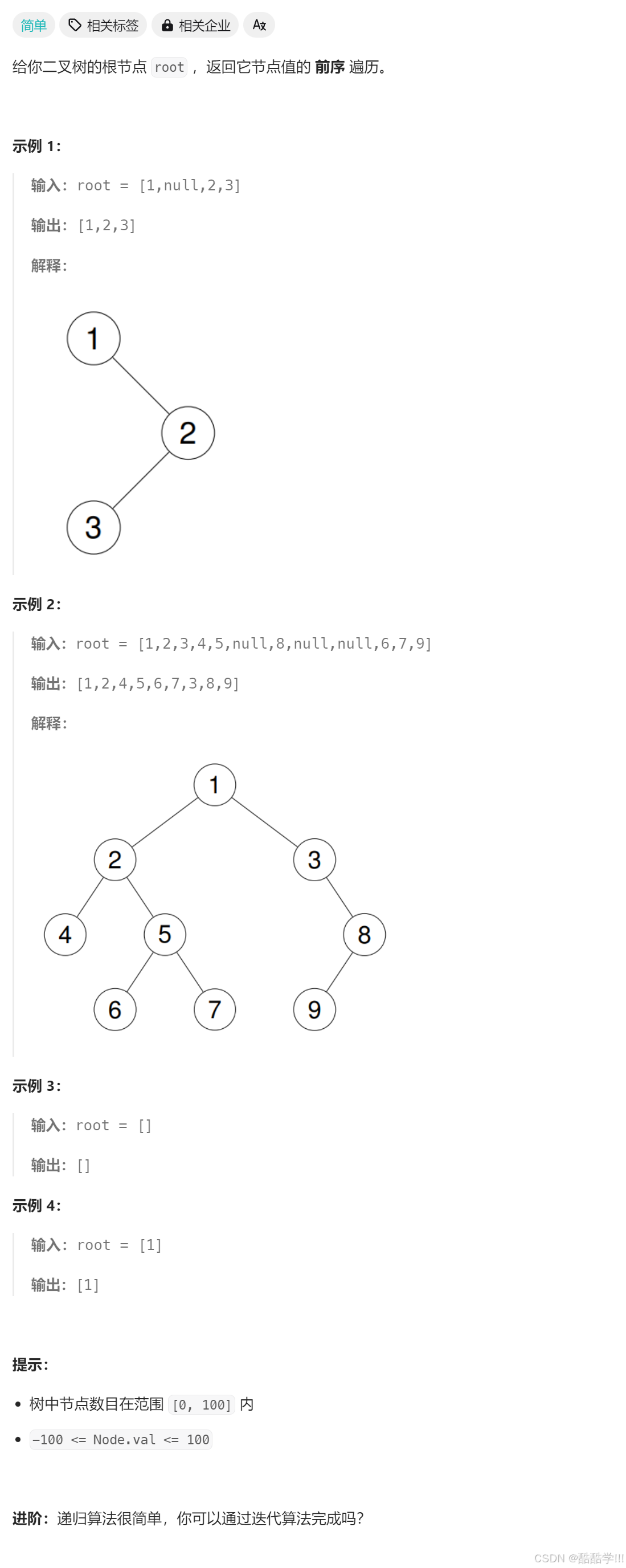
题目描述:
题目思路:
在二叉树初阶刷题阶段, 我们已经实现了前序遍历的递归实现, 但是递归层数多会造成栈溢出, 所以对于非递归的实现, 我们也要掌握, 其实原理也很简单, 就是模拟递归实现的过程, 先创建一个栈, 用于记录根模拟递归的过程, 遍历左节点, 遍历之前先入栈, 此题前序遍历, 所以直接将此节点的val也插入到vector中, 直到遍历到nullptr,次时说明左子树已全部遍历完, 接着去栈顶元素, 出栈顶元素, 并且将栈顶元素的right赋值给cur,进行下一次的循环遍历, 直至栈为空, 结束的条件cur不为空说明还有右子树需要遍历, 栈不为空说明还有左子树需要遍历右子树.
代码实现:
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */class Solution {public://非递归前序遍历 vector<int> preorderTraversal(TreeNode* root) { vector<int> v; TreeNode* cur = root; stack<TreeNode*> snode; while(cur || !snode.empty()) { while(cur) { v.push_back(cur->val); snode.push(cur); cur = cur->left; } TreeNode* top = snode.top(); snode.pop(); cur = top->right; } return v; }};9. 二叉树中序遍历 ,非递归迭代实现
题目连接: 二叉树的中序遍历
题目描述:
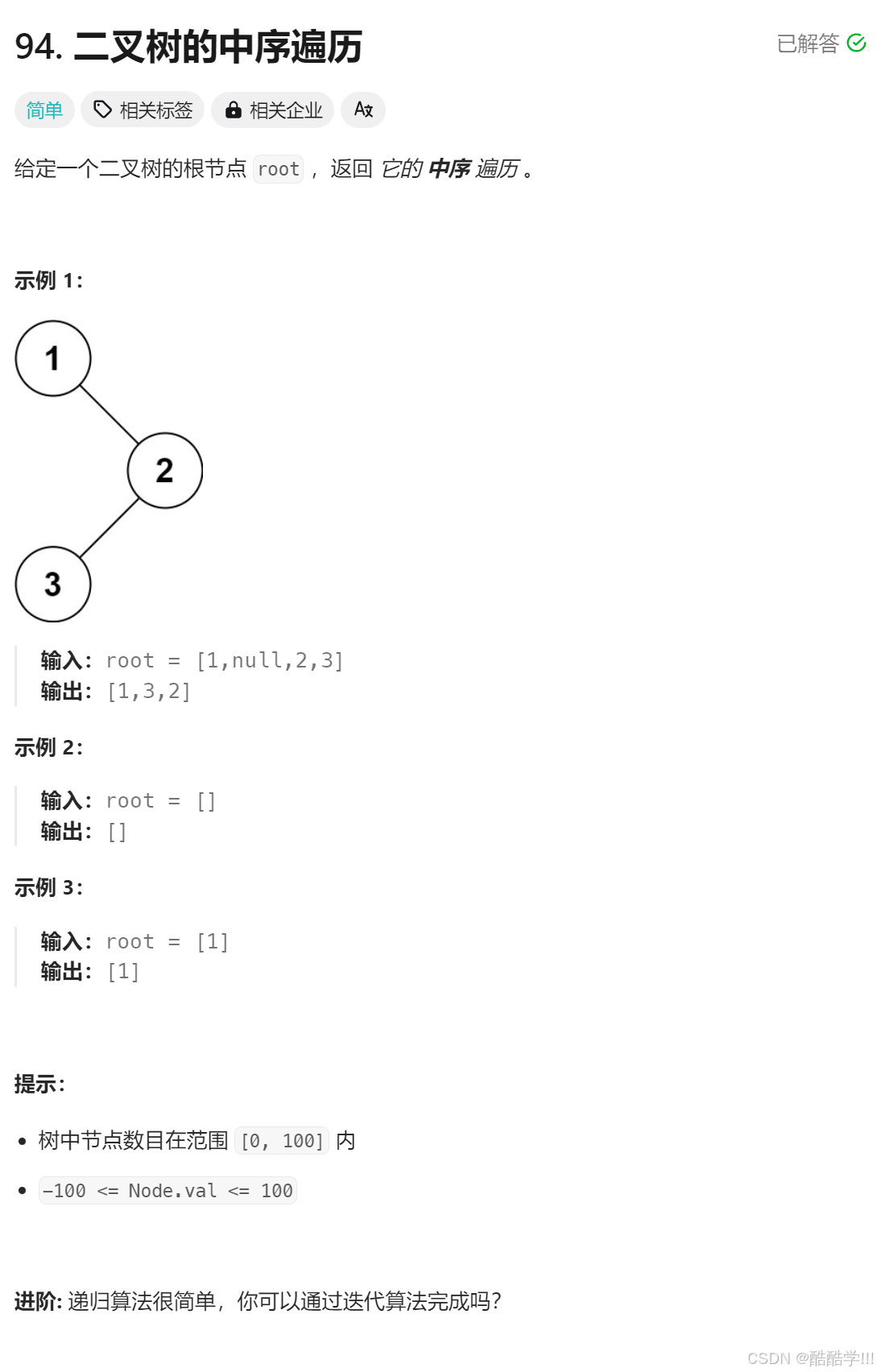
题目思路:
本题要求中序遍历, 基本思路与前序遍历差不多, 模拟递归的实现过程, 只不过, 本次我们左子树入栈不要进行访问, 而是遍历到左子树为nullptr时, 回退的过程在进行访问, 然后在访问右子树, 右子树也是一样的操作, 遇到不为空先不访问, 先入栈,直到栈为空时, 在进行访问, 此时访问的效果就达到 左 根 右.
代码实现:
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */class Solution {public: vector<int> inorderTraversal(TreeNode* root) { vector<int> v; stack<TreeNode*> snode; TreeNode* cur = root; while(cur || !snode.empty()) { while(cur) { snode.push(cur); cur = cur->left; } TreeNode* top = snode.top(); v.push_back(top->val); cur = top->right; snode.pop(); } return v; }};10. 二叉树的后序遍历 ,非递归迭代实现
题目连接: 二叉数的后序遍历
题目描述:
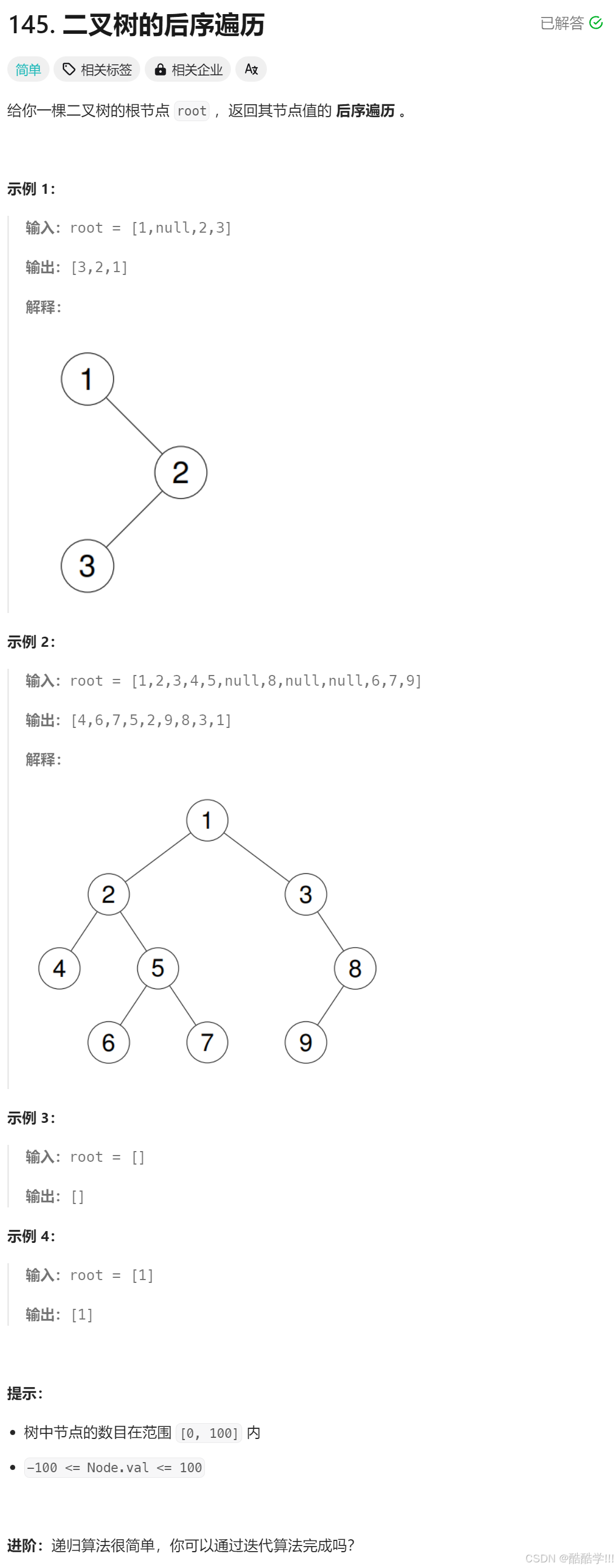
题目思路:
还是双循环模拟递归的实现过程, 遇到节点先不放问, 先入栈, 但是我们需要先访问左, 在访问右, 最后访问根, 所以左子树遍历到空之后, 取栈顶元素访问右子树, 如果右子树为根的情况我们才能访问, 访问完之后, 出栈, 在取栈顶元素, 问题就来了, 这时又会取到栈顶元素的右子树, 那我们是否还需要再进去访问呢, 如果访问过了我们就不要访问了, 直接访问此节点, 没访问过在进行访问, 不然会陷入死循环, 这是我们额为创建一个指针来记录上一次出栈的节点, 也就是上一次访问过的节点, 如果为top->right那么就不用进入循环了, 直接pop并直接访问该节点即可, 通过模拟我们可以发现, 其实不管怎么样, 后序遍历一定是先访问的是右子树为空的那个节点.
代码实现:
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */class Solution {public: vector<int> postorderTraversal(TreeNode* root) { stack<TreeNode*> snode; TreeNode* cur = root; TreeNode* prev = nullptr; vector<int> v; while(cur || !snode.empty()) { while(cur) { snode.push(cur); cur = cur->left; } TreeNode* top = snode.top(); if(top->right == nullptr || prev == top->right) { v.push_back(top->val); prev = top; snode.pop(); } else { cur = top->right; } } return v; }};完 这些进阶题目我们也需要进行掌握, 这样才能运筹帷幄, 创作不易 感谢点赞关注!!!