一、优化问题概述
1.优化问题概述
设计变量、目标函数、约束
2.优化问题求解步骤
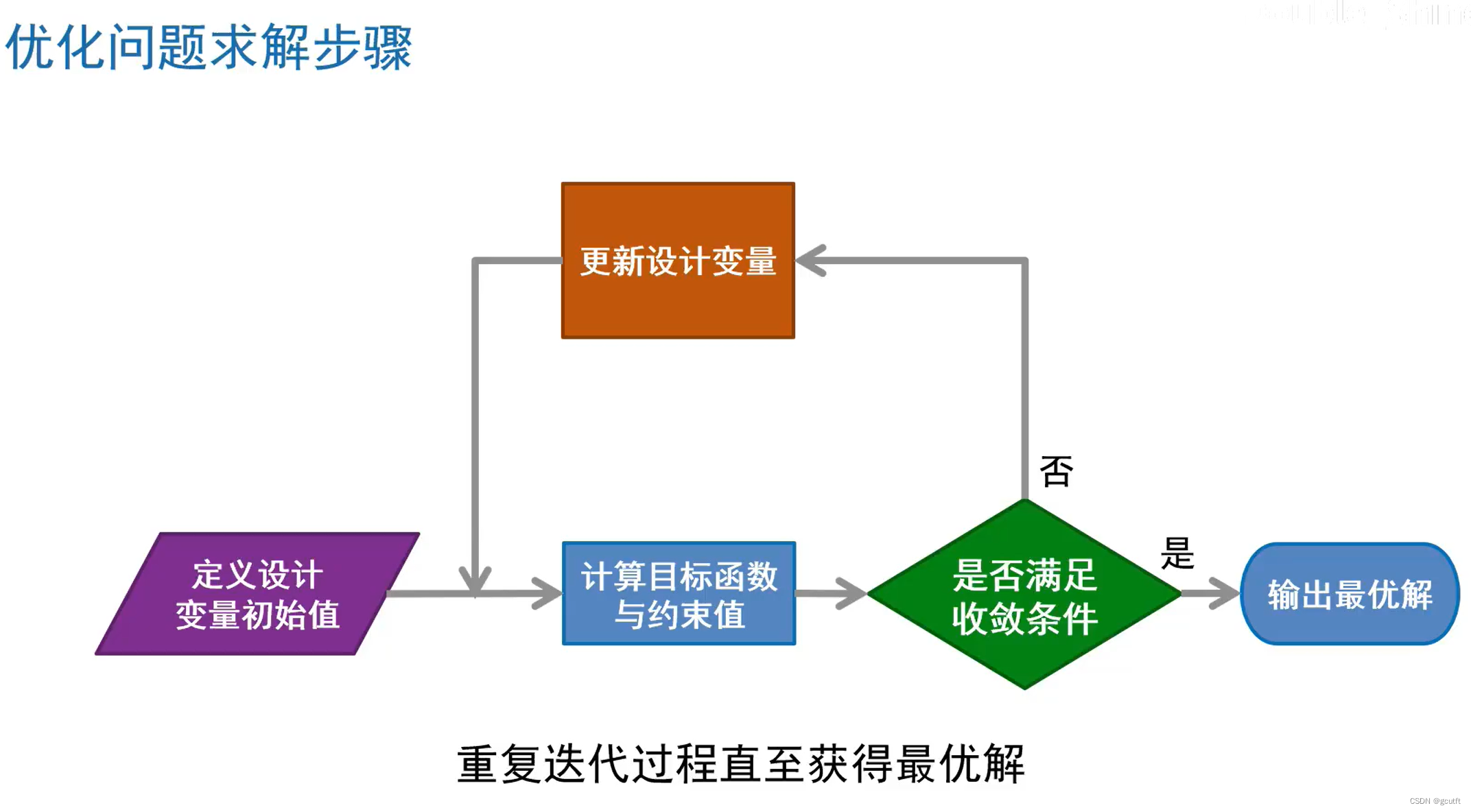
3.优化问题分类

二、Optimization Toolbox---优化工具箱
可在MATLAB帮助中心进行查看

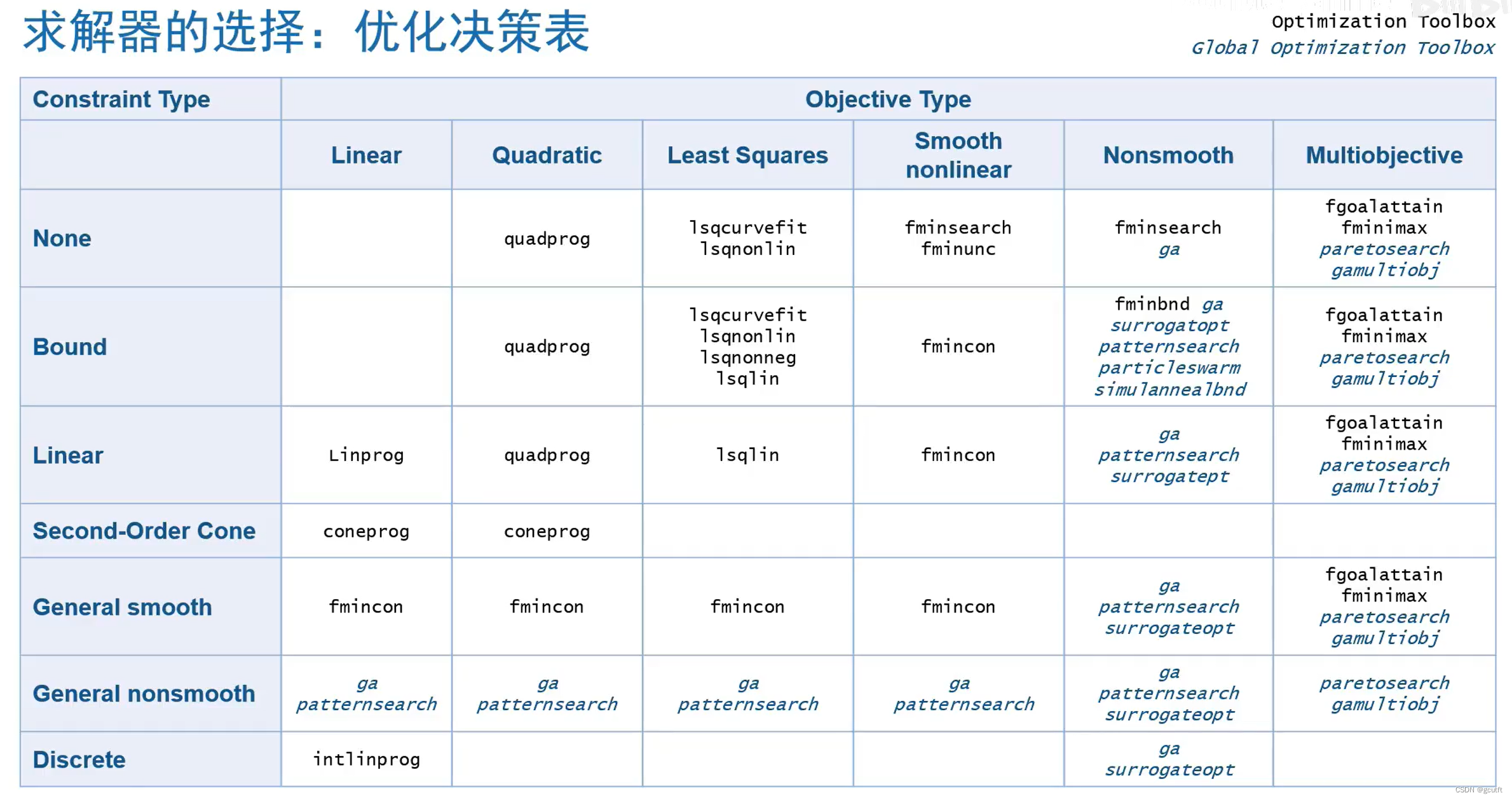
1.使用实时编辑器“优化”任务求解 (交互式)
示例:
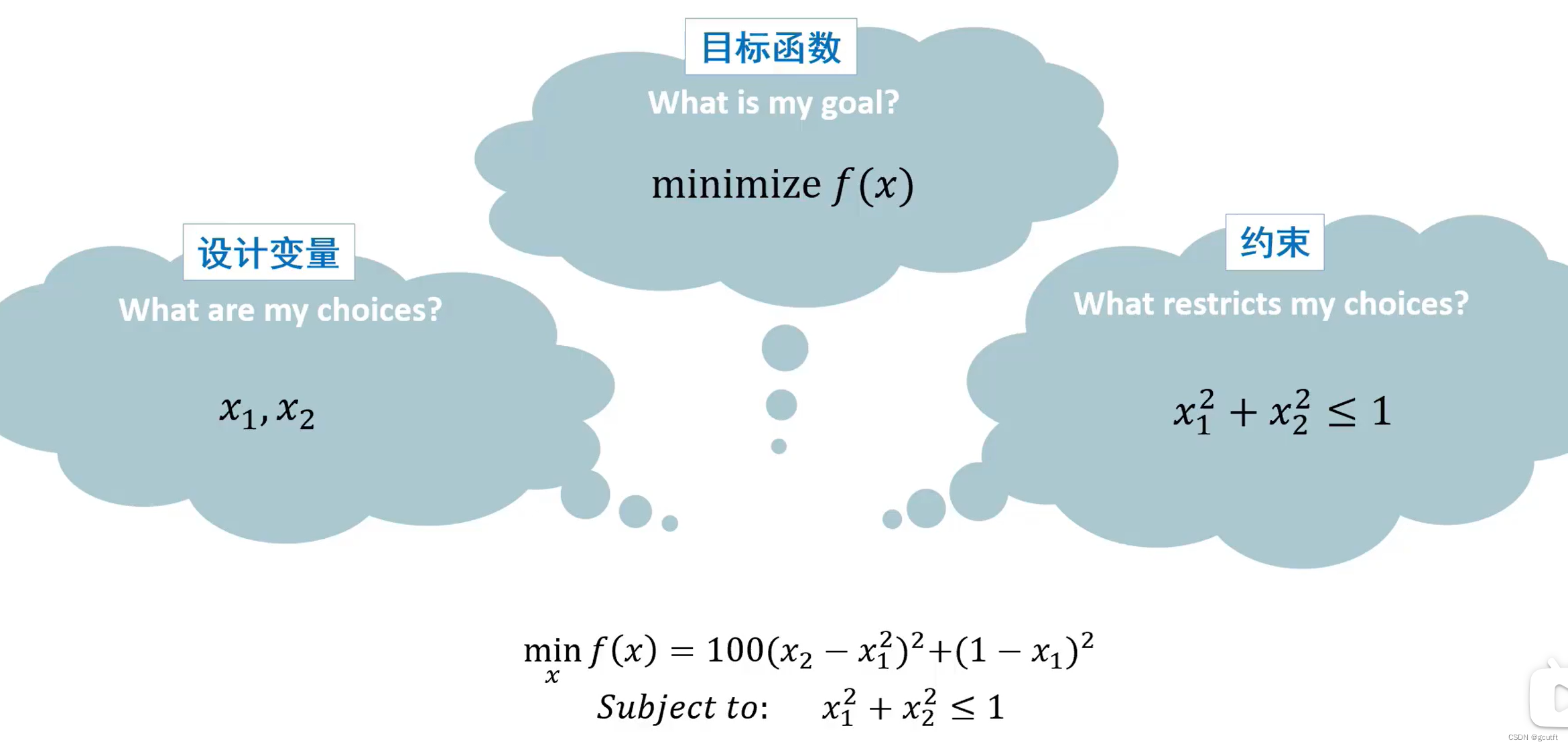
实时编辑器任务:
执行特定操作的APP
缩短开发时间
缩短绘图时间
减少错误
可自动生成代码
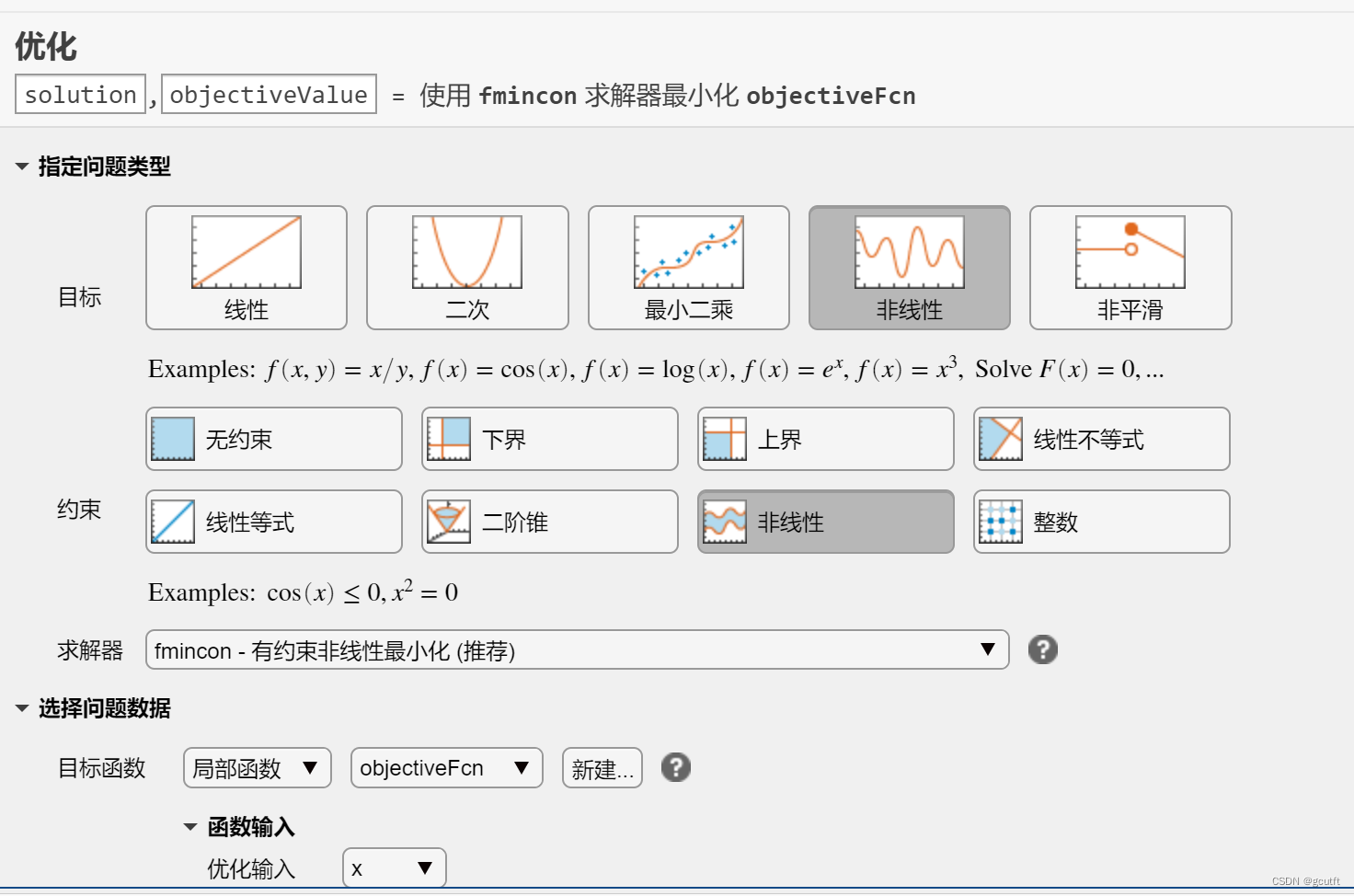
操作步骤:
1.选择目标函数与约束类型
2.选择求解器
3.提供相应数据
4.根据模板设置目标函数与约束
5.设置显示选项
6.求解
生成代码:基于“求解器”求解
2.基于“问题”求解优化问题(编程)
优势:
1.代码表述与数学公式一致,易于创建和调试
2.自动选择求解器、处理不同约束类型
3.提供fcn2optimexpr将函数转化为所需表达式
4.自动计算梯度
自动微分:对目标函数与约束自动计算梯度
1.一系列自动计算梯度的数值方法
无需使用符号表达式运算
仅支持一阶梯度
2.与有限差分法相比
计算量减小
计算精度高
3.需满足一定条件
示例: 使用MATLAB求解数独
求解思路:这是一个0/1优化问题
操作步骤:
1.定义优化变量
2.建立优化问题“容器”【目标函数表达式、约束表达式、初始值...】
3.定义目标函数表达式
4.设置初始值
5.求解
3.基于“求解器”求解---需要对优化算法有一定了解
优势:
1.可以使用实时编辑器“优化”任务进行可视化操作
2.矩阵形式表达,求解时间更短
3.可以在大型问题中使用Hessian矩阵乘法函数或jacobian矩阵乘法函数来节省内存
4.可以提供梯度或Hessian矩阵提高精度与效率


选择求解器
使用矩阵与向量定义目标函数与约束
使用函数定义目标函数与约束
调用求解器
操作步骤:
1.选择求解器
2.编写目标函数
3.编写约束
4.设置选项
5.调用求解器求解
三、Global Optimization Toolbox---全局优化工具箱
使用fmincon寻找全局最优解依赖于初始值
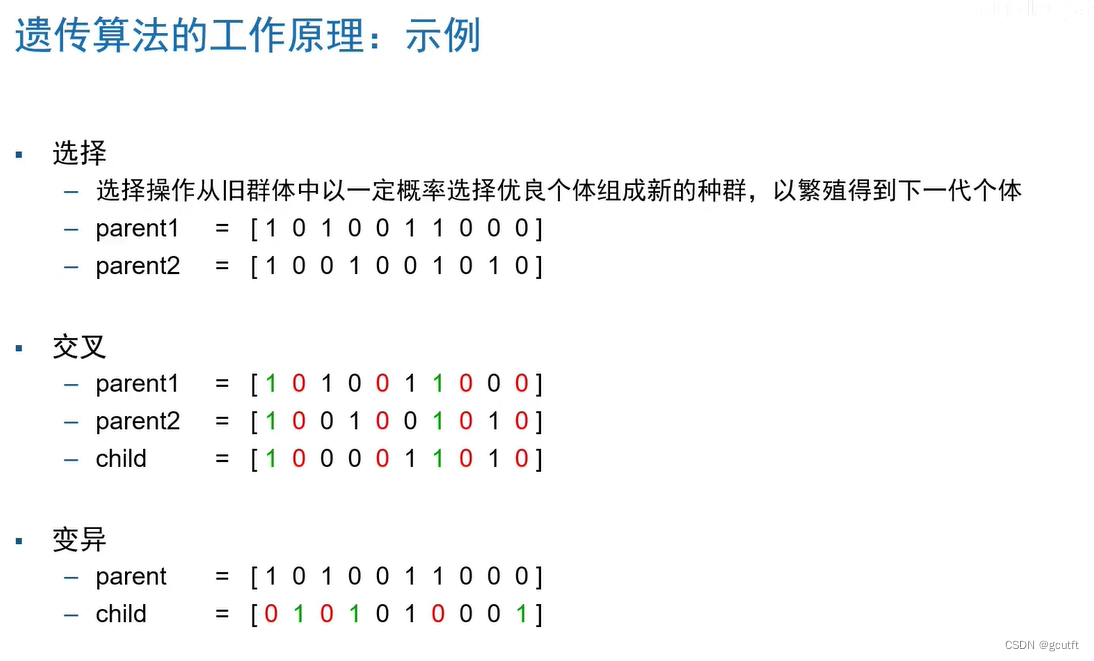
全局优化工具箱:求解器

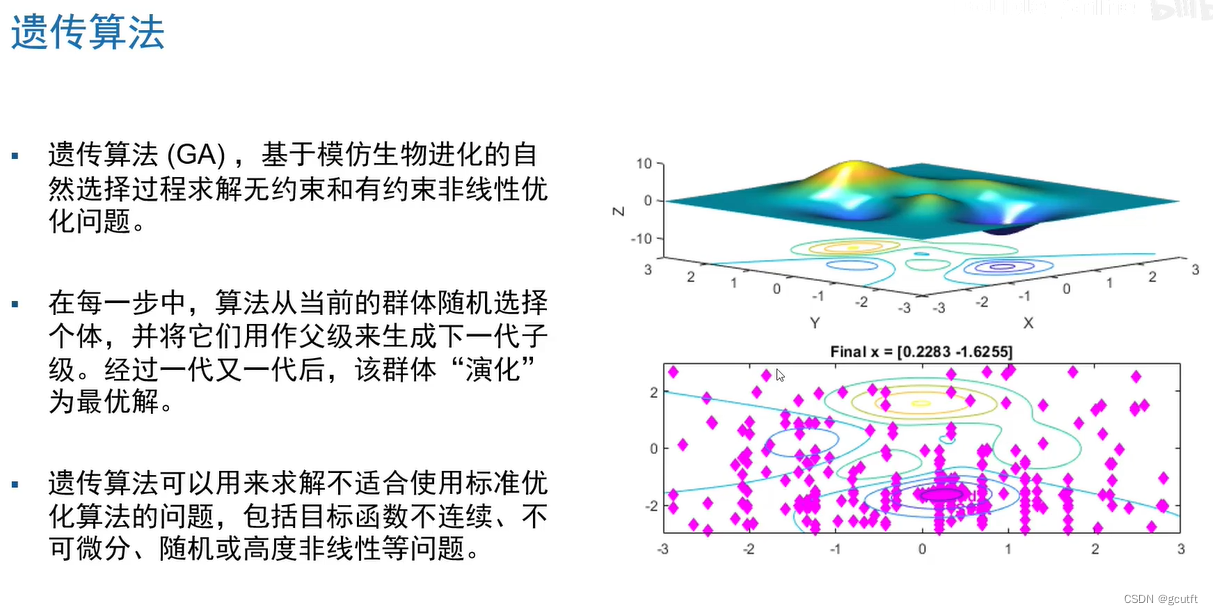
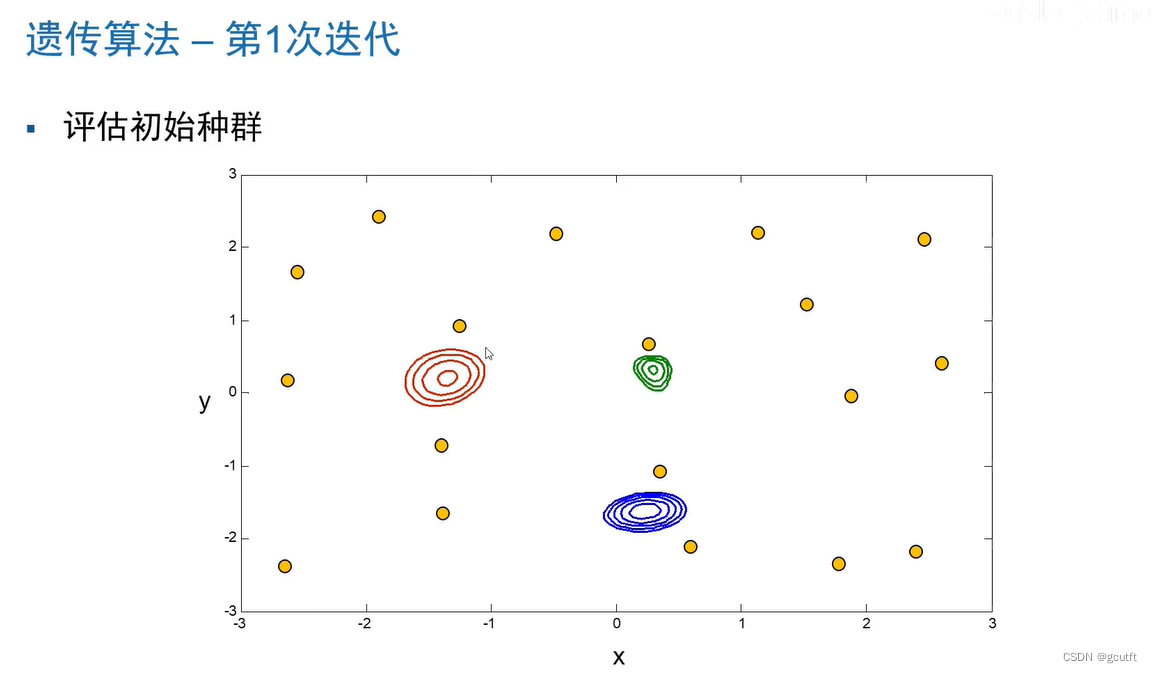
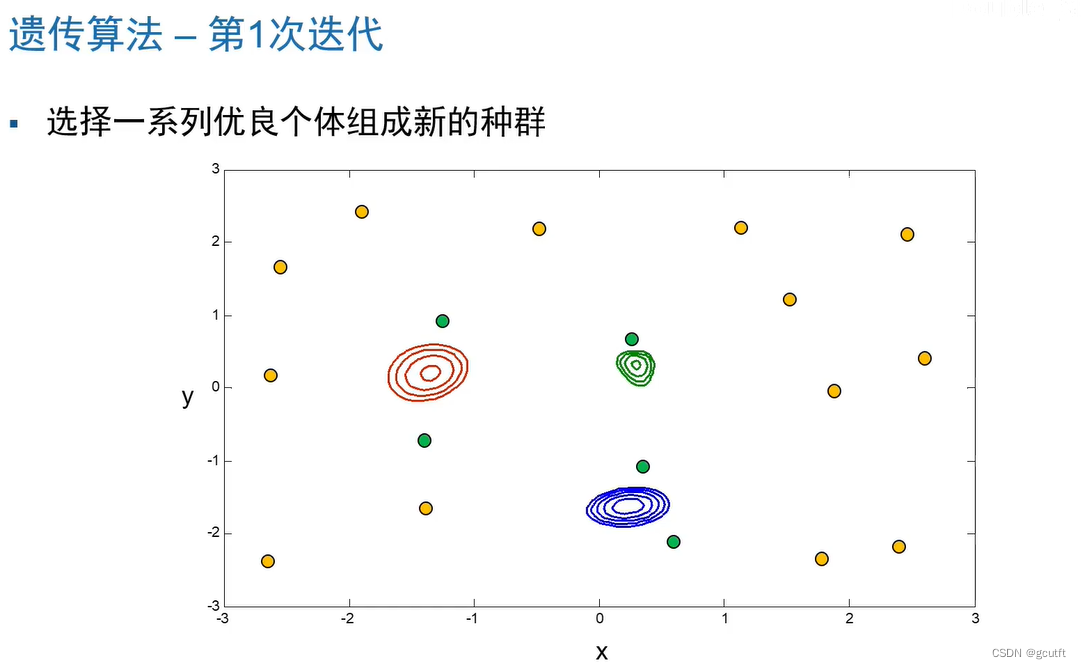
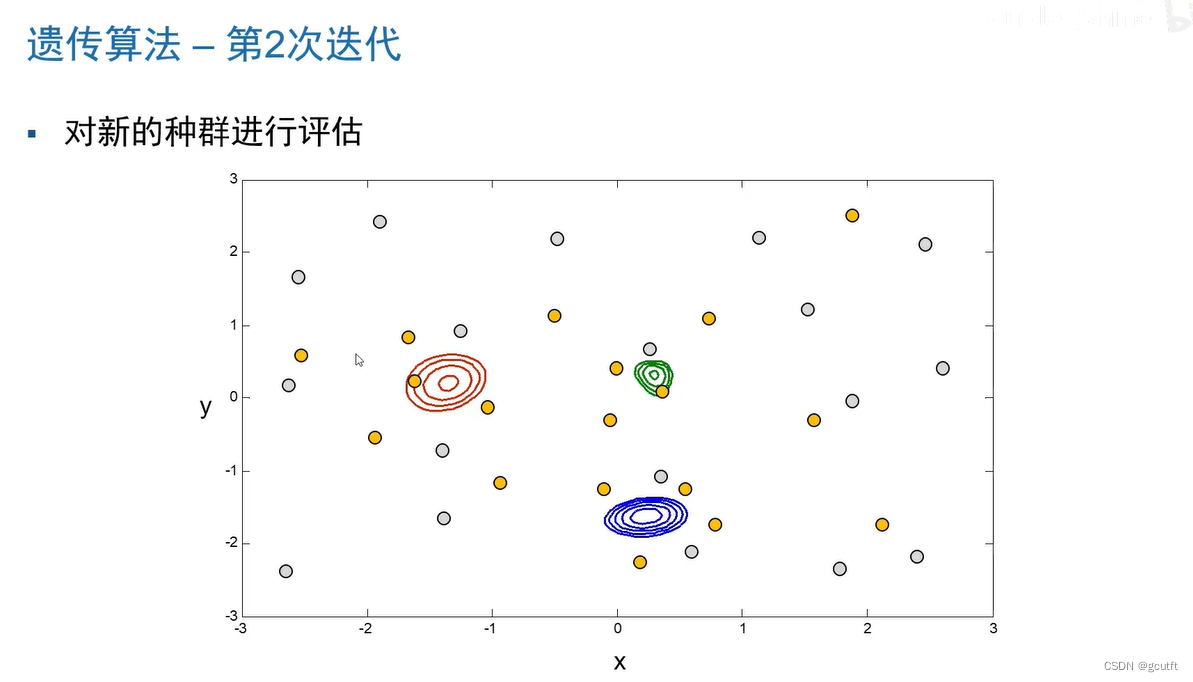
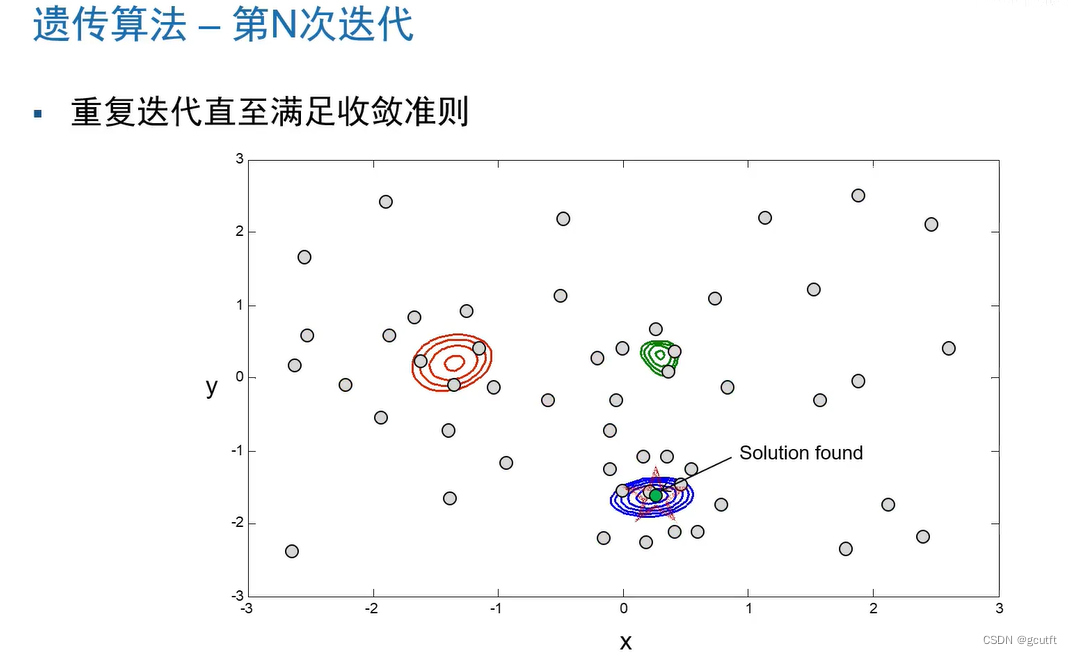
黄色点---初始种群
三个圈---三个局部最优解
蓝色圈---本问题的全局最优解