目录
0 专栏介绍1 N N N圆覆盖碰撞模型2 圆与矩形的碰撞检测3 算法仿真与可视化3.1 核心算法3.2 仿真实验
0 专栏介绍
?课设、毕设、创新竞赛必备!?本专栏涉及更高阶的运动规划算法轨迹优化实战,包括:曲线生成、碰撞检测、安全走廊、优化建模(QP、SQP、NMPC、iLQR等)、轨迹优化(梯度法、曲线法等),每个算法都包含代码实现加深理解
?详情:运动规划实战进阶:轨迹优化篇
本期实现如下的碰撞检测效果
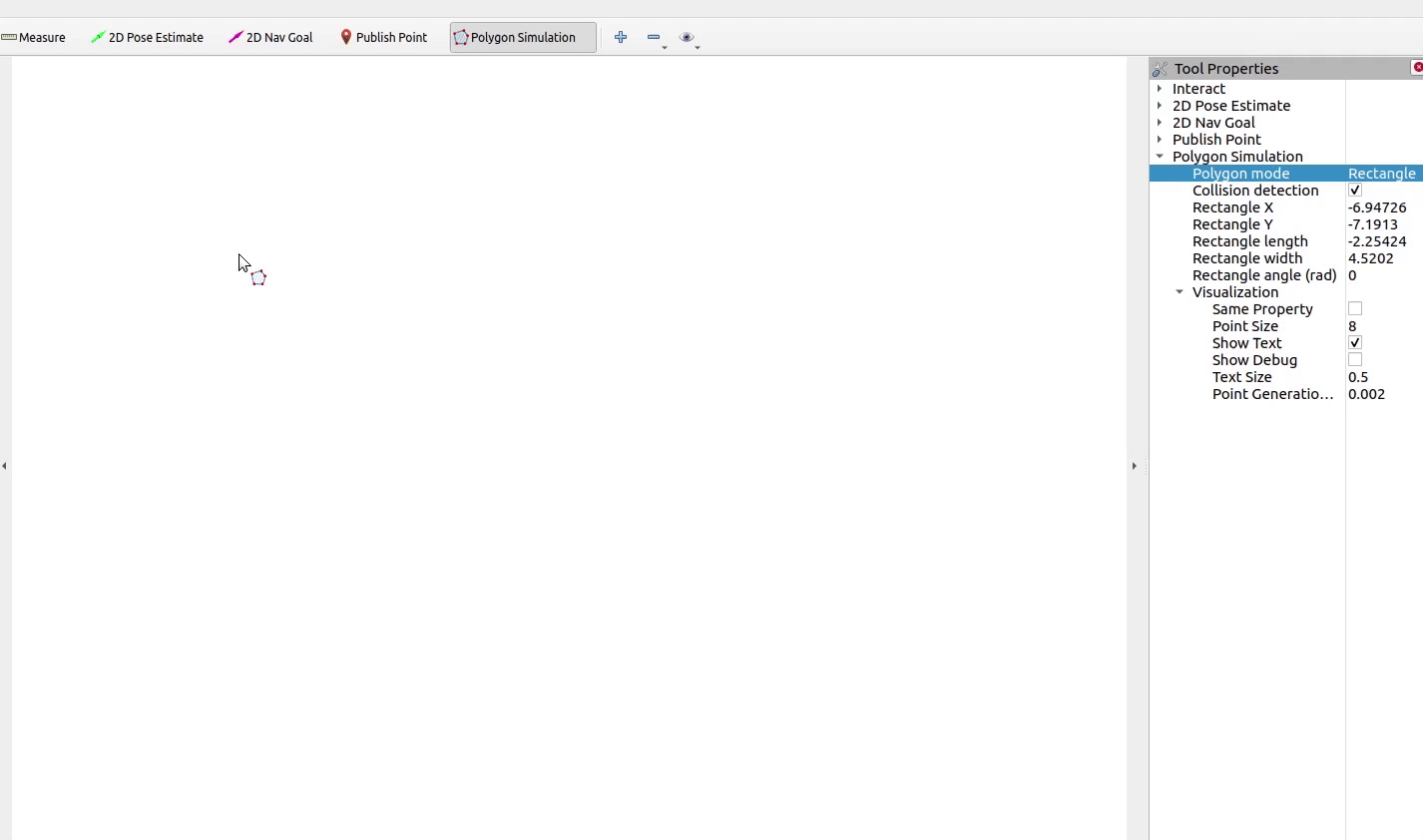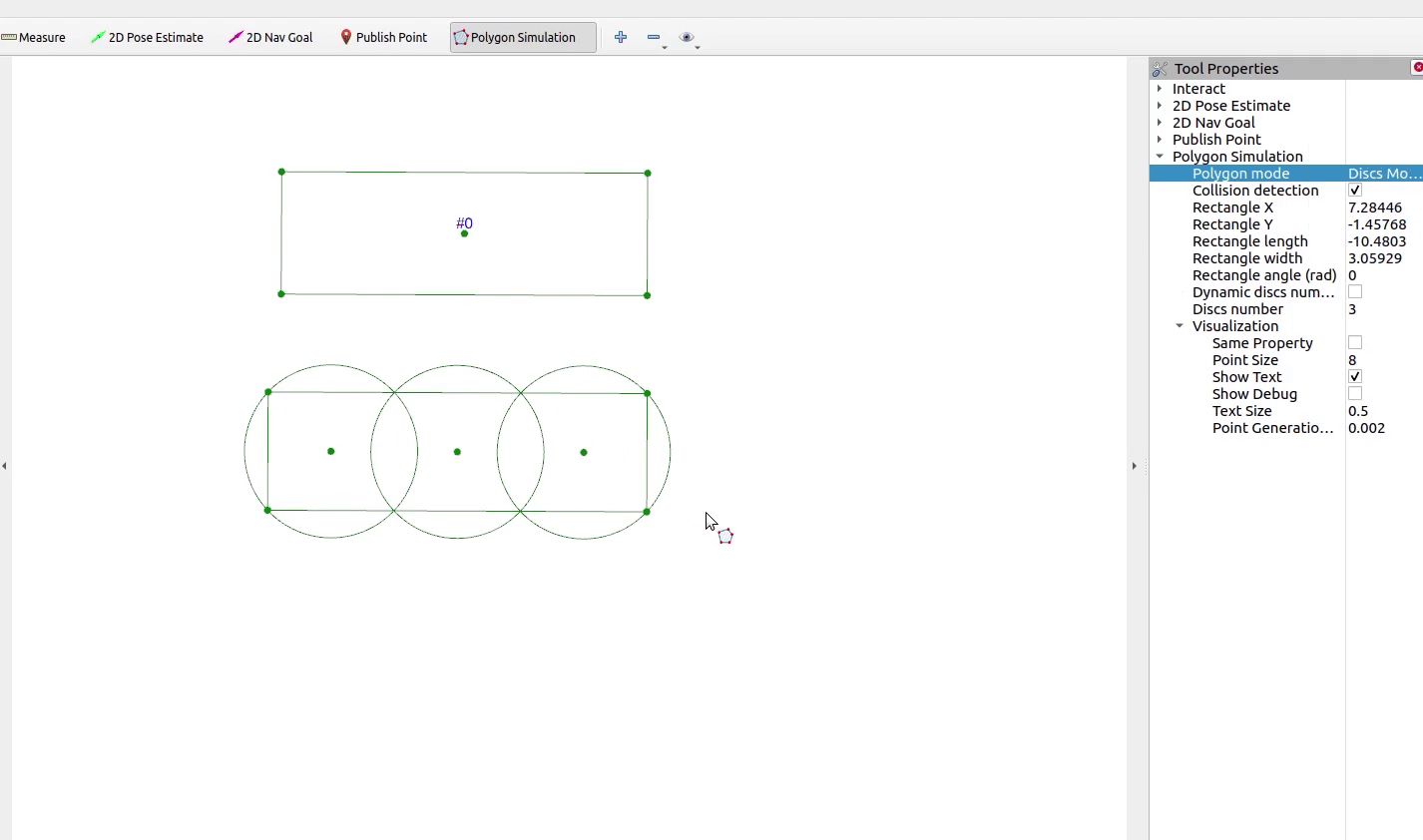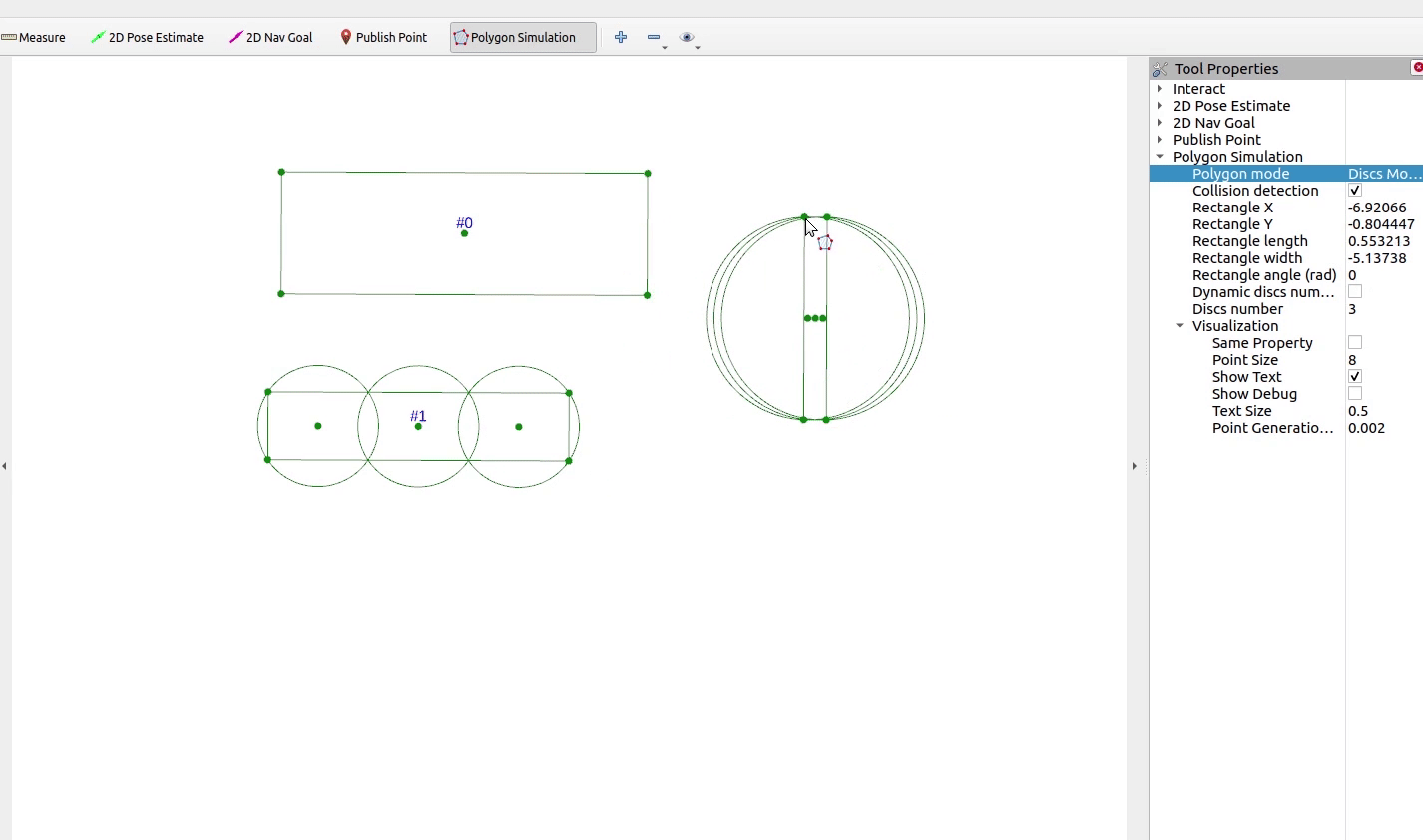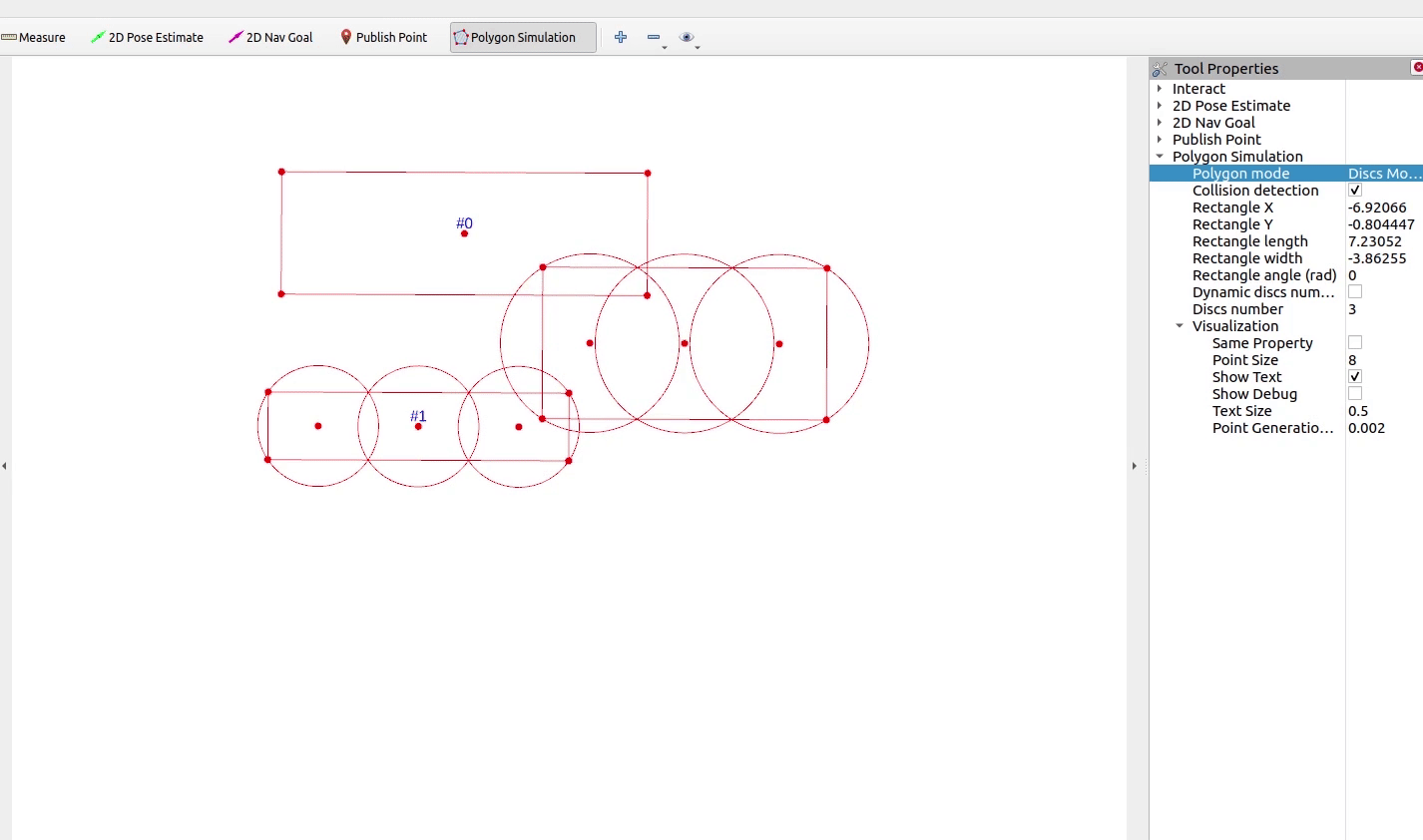
1 N N N圆覆盖碰撞模型
在车辆的路径规划过程中,需要评估和避开可能的障碍物。 N N N圆覆盖碰撞检测算法可以快速检测和响应路径上的障碍物,从而优化行驶路线。
直观地,如图所示,采用单个外接圆包围物体,此时只需要检查圆心和半径的关系即可实现碰撞检测。然而这种方法容易造成自由空间狭窄,更精细的做法是利用 个圆盘覆盖物体,对这些圆依次进行单圆碰撞检测,如图所示
形式化地,设自车后轴中心坐标为 ( x , y ) (x, y) (x,y),由几何关系可知
{ x i d i s c = x + ( 2 i − 1 2 N ⋅ ( L 1 + L 2 ) − L 1 ) cos θ y i d i s c = y + ( 2 i − 1 2 N ⋅ ( L 1 + L 2 ) − L 1 ) sin θ i = 1 , 2 , ⋯ , N \begin{cases} x_{i}^{\mathrm{disc}}=x+\left( \frac{2i-1}{2N}\cdot \left( L_1+L_2 \right) -L_1 \right) \cos \theta\\ y_{i}^{\mathrm{disc}}=y+\left( \frac{2i-1}{2N}\cdot \left( L_1+L_2 \right) -L_1 \right) \sin \theta\\\end{cases}\,\,i=1,2,\cdots ,N {xidisc=x+(2N2i−1⋅(L1+L2)−L1)cosθyidisc=y+(2N2i−1⋅(L1+L2)−L1)sinθi=1,2,⋯,N
其中 θ \theta θ是航向角; N N N是覆盖圆的数量, N N N越大碰撞检测越精细但同时计算负担更大。圆的半径由 N N N和自车几何形状唯一确定
R d i s c = ( L 1 + L 2 2 N ) 2 + ( W 2 ) 2 R^{\mathrm{disc}}=\sqrt{\left( \frac{L_1+L_2}{2N} \right) ^2+\left( \frac{W}{2} \right) ^2} Rdisc=(2NL1+L2)2+(2W)2
2 圆与矩形的碰撞检测
如图所示,核心原理是计算圆心与矩形的最短距离 ∣ u ∣ \left| \boldsymbol{u} \right| ∣u∣,若 ∣ u ∣ < r \left| \boldsymbol{u} \right|<r ∣u∣<r则两者相交。算法上,首先考虑无旋转的矩形,不失一般性地将圆投影到第一象限,得到
v = [ ∣ p x − c x ∣ ∣ p y − c y ∣ ] T \boldsymbol{v}=\left[ \begin{matrix} \left| p_x-c_x \right|& \left| p_y-c_y \right|\\\end{matrix} \right] ^T v=[∣px−cx∣∣py−cy∣]T
其中 p \boldsymbol{p} p与 c \boldsymbol{c} c分别是矩形和圆的中心向量。设 l − l^- l−、 w − w^- w−分别为矩形长、宽的一半,则矩形中心到第一象限顶点向量为 h = [ l − w − ] \boldsymbol{h}=\left[ \begin{matrix} l^-& w^-\\\end{matrix} \right] h=[l−w−],从而得到最近距离向量
u = [ max ( v x − h x , 0 ) max ( v y − h y , 0 ) ] T \boldsymbol{u}=\left[ \begin{matrix} \max \left( v_x-h_x, 0 \right)& \max \left( v_y-h_y, 0 \right)\\\end{matrix} \right] ^T u=[max(vx−hx,0)max(vy−hy,0)]T
即将负数分量设为0;再比较 ∣ u ∣ \left| \boldsymbol{u} \right| ∣u∣和圆的半径大小关系即可
推广到一般情形,设矩形旋转角度为 α \alpha α,则只需要将 v \boldsymbol{v} v反向旋转 α \alpha α角度即可转换为无旋转的场景,算法流程如下所示
3 算法仿真与可视化
3.1 核心算法
核心算法如下所示
圆与矩形的碰撞检测
auto other_rect = std::dynamic_pointer_cast<VRectangle>(other);for (const auto& disc : discs_){ auto v = disc.first - other_rect->center(); // rotate ang project first quadrant float theta = -other_rect->angle(); float rotate_vx = std::fabs(v.x * std::cos(theta) - v.y * std::sin(theta)); float rotate_vy = std::fabs(v.x * std::sin(theta) + v.y * std::cos(theta)); // right-top point of rectangle float h_x = std::fabs(other_rect->length()) / 2.0f; float h_y = std::fabs(other_rect->width()) / 2.0f; // closest vector float u_x = std::max(0.0f, rotate_vx - h_x); float u_y = std::max(0.0f, rotate_vy - h_y); if (std::hypot(u_x, u_y) < disc.second) return true;}return false;圆与圆的碰撞检测
auto other_circle = std::dynamic_pointer_cast<VCircle>(other);const auto& other_circle_center = other_circle->center();const auto& other_circle_radius = other_circle->radius();for (const auto& disc : discs_){ if (std::hypot(other_circle_center.x - disc.first.x, other_circle_center.y - disc.first.y) <= disc.second + other_circle_radius) return true;}return false;3.2 仿真实验
通过Rviz->Add New Tool添加Polygon Simulation插件
开启碰撞检测功能后,验证 N N N圆覆盖碰撞检测算法
单圆碰撞与无碰撞情形完整工程代码请联系下方博主名片获取
? 更多精彩专栏:
《ROS从入门到精通》《Pytorch深度学习实战》《机器学习强基计划》《运动规划实战精讲》…?源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系?