参考文献：
[1] Deb K , Jain H .An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints[J].IEEE Transactions on Evolutionary Computation, 2014, 18(4):577-601.DOI:10.1109/TEVC.2013.2281535.
非支配排序遗传算法(Non-dominated Sorting Genetic Algorithms，NSGA)是最经典的多目标优化算法之一，在NSGA算法的基础上，目前已经更新了NSGA-Ⅱ和NSGA-Ⅲ两种算法。NSGA-Ⅲ算法又称为NSGA3算法，第三代非支配排序遗传算法，第三代多目标遗传算法，这篇博客主要对NSGA-Ⅲ算法的原文献进行解读，重点介绍NSGA-Ⅲ算法的实现原理。
1.引言
由于传统的多目标优化已经很难满足水论文的目的了，因此现在多目标优化的研究主要集中在超多目标优化(many-objective optimization)，也就是四个以上目标函数的优化问题。而超多目标优化问题的研究也凸显了NSGA-Ⅱ及其他一些传统多目标优化算法的不足之处：
1）非支配解的数量爆炸式增长。超多目标优化问题中非支配解的数量呈指数级别增加，如何筛选和存储非支配解成为难题；
2）种群多样性评估的算法效率问题。超多目标优化问题中进行种群的选择操作时，为保证种群多样性，采用拥挤距离或聚类算子的计算效率很低，时间和空间复杂度都会变得很高；
3）种群重组策略的作用存疑。在超多目标优化问题中，不同的解之间的欧氏距离一般都较远，通过不同解信息相结合得到的新解的距离一般也会很远，这样更新的效果存疑。
4）不同优化目标的权衡面表示困难。需要用更大规模的解集才能表示帕累托前沿，同时很难从解集中选择适当的方案。
5）帕累托前沿可视化困难。不同于2目标或者3目标问题，超多目标优化问题的帕累托前沿难以用图像展示。
针对非支配解计算效率相关的问题，通常有两种不同的解决方法，其中一种方法是通过设置特殊支配原则(如ε支配原则)进行缓解。通过ε-支配，可以在很大程度上减少非支配解的数量，提高算法的搜索效率。
而在NSGA-Ⅲ算法中，针对种群多样性评估的算法效率等问题，采用了预定义的参考点对搜索方向进行引导。通过预先构造均匀分布的参考点对算法搜索方向进行引导，可以使得生成的帕累托前沿也尽可能均匀分布，即使在超多目标优化中也无需存储大规模非支配解集即可表示出帕累托前沿。针对种群重组策略的问题，NSGA-Ⅲ采用了对重组操作的个体进行限制的方式，只有处于相邻参考点的解之间才会发生重组操作，可以避免无效的重组操作。
2.相关概念的解释
引言中存在一些较新的概念，下面分别对这些概念进行简单说明，后面也会结合算法原理进一步解释。
2.1 ε-支配
在多目标进化算法中，ε-支配是一种改进的支配关系定义，用于解决传统Pareto支配关系的局限性。传统Pareto支配关系要求一个解在所有目标函数上都不劣于另一个解。然而，超多目标优化中，这种支配关系将导致非支配解数量过多。ε-支配通过引入一个小的正数ε来修正支配关系的定义。仅当一个解在所有目标上都比另一个解更优，且数值差在ε以上才认为其中一个解支配另一个解。举例说明：
对于多目标优化问题min {f1,f2,f3,f4}，设定ε=0.05，假设有两个解A=[1.5, 1.5, 1.5, 1.5]，B=[1.46, 1.7, 1.48, 1.9]，按照传统支配关系定义，解A和解B互不支配，为一组非支配解，但如果按照ε-支配的定义，A ≤ B+ε = [1.51, 1.75, 1.53, 1.95]，因此在ε-支配的定义下，可以认为解A支配解B。同理可得，通过使用ε-支配原则，可以大量减少非支配解的数量。
2.2 参考点
参考点常常被用来解决多目标优化问题上的收敛性和多样性问题，使用预定义的参考点可以指导NSGA-Ⅲ算法搜索解空间的方向，使得算法会更加倾向于搜索那些距离参考点较近的解。此外，参考点的分布会影响到生成的非支配解的多样性。如果参考点分布均匀，NSGA-Ⅲ算法就可以在 Pareto 前沿上找到尽可能广泛的解。
举例说明：
假设我们将租房子看做一个双目标优化问题，其中一个优化目标是最小化租金，另一个目标是最大化房子的面积，优化问题表示为{min Price, max S}。假设备选方案中租金的的范围是[2000,5000]元/月，面积的范围是[40,130]平方米。这种情况下，我们可以选择3个参考点：参考点1为{5000,140}，即面积最大但租金最高，参考点2为{2000,40}，即租金最便宜但面积最小，参考点3为{3500,85}，即中等租金和中等面积。
从上面的例子可以看到，所选的参考点不一定是优化问题的可行方案，但是可以表示不同目标之间的平衡。同样针对上面的问题，如果需要更多的参考点，我们可以把每个优化目标分为更多份数，租金分为低租金(2000元/月)，较低租金(3000元/月)，较高租金(4000元/月)和高租金(5000元/月)，面积分为小面积(40平方米)，较小面积(70平方米)，较大面积(100平方米)和大面积(130平方米)，这种情况下可以得到更多参考点：
{5000,130}——高租金，大面积；{4000,100}——较高租金，较大面积；{3000,70}——较低租金，较小面积；{2000,40}——低租金，小面积；如果需要把每个目标函数分为更多的份数，可以得到更多的参考点。NSGA-III算法就是像这样利用预定义的参考点对选择个体的方法进行改进，以维持种群之间的多样性。NSGA-III算法中求解参考点的具体方法将在博客的3.2节进行介绍。
3.NSGA-Ⅲ算法步骤
我们先给出论文中提供的伪代码：
从伪代码可以看到，NSGA-Ⅲ算法主要思路如下：种群初始化→进入主循环→交叉操作→变异操作→种群更新操作→选择操作→输出全局最优解。
NSGA-Ⅲ算法和NSGA-Ⅱ算法最主要的区别就是选择操作上，将基于拥挤度距离排序的方法改为基于参考点排序的方法。下面将详细介绍NSGA-Ⅲ算法求解过程。
3.1 目标函数的自适应归一化处理
实际的多目标优化问题中，不同目标的量纲、单位、取值范围都有可能不一样，为了能将不同的优化目标进行对比，需要将其进行归一化。NSGA-Ⅲ算法中采用的自适应归一化处理方法的伪代码如下：
从上面的伪代码可知，自适应归一化处理的步骤为：确定种群的理想点→根据理想点对目标函数进行转换→确定种群的极值点→计算超平面和坐标轴的截距→归一化目标函数。具体如下：
1）确定种群的理想点
种群的理想点就是各个目标函数的最优值，假设所有目标都是min形式，那么理想点可以表示如下：
以我们上面提到的租房子优化问题为例，假设种群中包含4个个体，每个个体的目标函数值为：
(3500,80),(2600,50),(4700,115),(3900,110)。
首先为了计算方便，我们通过添加负号的形式将所有优化目标均转为最小化形式{min Price, min -S}，转换后的4个个体为：
(3500,-80),(2600,-50),(4700,-115),(3900,-110)。
那么可以计算出种群的理想点：
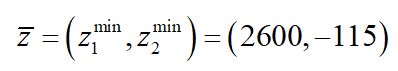
2）根据理想点对目标函数进行转换
在计算出理想点后，就需要将每个个体的目标函数值减去对应维的理想点目标函数值，从而对目标函数进行转换，公式如下：
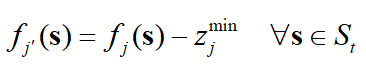
对上述租房优化问题，目标函数转换如下：
个体1转换后的目标函数=(3500,-80)-(2600,-115)= (900,35)个体2转换后的目标函数=(2600,-50)-(2600,-115)=(0,65)个体3转换后的目标函数=(4700,-115)-(2600,-115)=(2100,0)个体4转换后的目标函数=(3900,-110)-(2600,-115)=(1300,5)3）确定种群的极值点
种群的极值点数目和优化目标的数目相同，其中第k维的极值点就是在第k个目标函数上的取值很大，其他目标函数的取值很小。论文中使用权重向量w得到极值点：当计算第k维的极值点时，需要将该方向的权重wk设定为1，即wk=1，其他方向的权重设定为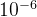
，再使用ASF函数得到每个个体的ASF值，ASF值最小的个体即为该目标方向的极值点。其中ASF函数公式如下：
经步骤2转换后的4个个体分别为：(900,35),(0,65),(2100,0),(1300,5)，当求第1个目标方向的极值点时，设定权重向量w=(1,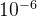
)，则4个个体的ASF值分别计算如下：
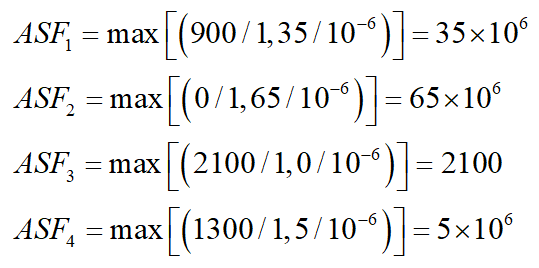
其中，第3个个体的ASF值最小，那么该个体就是第1个目标方向的极值点，为(2100,0)。
求第2个目标方向极值点时，设定权重向量w=(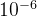
,1)，则4个个体的ASF值分别计算如下：
其中，第2个个体的ASF值最小，那么该个体就是第2个目标方向的极值点，为(0,65)。
4）计算超平面和坐标轴的截距
在求得极值点后，需要将极值点构成超平面，再计算超平面到各个坐标轴的截距。很容易发现，当目标函数的数量为M时，截距的数量也为M。以2维空间为例，截距式平面方程为
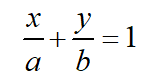
假设2个点的坐标分别为（x1,y1）和(x2,y2)，则带入上述平面方程，得出如下线性方程组：
推广到n维空间，线性方程组如下：
对于租房优化问题，已求出的两个极值点分别为(2100,0)和(0,65)，可以解出超平面到各个坐标轴的截距：
5）归一化目标函数
最后，需要根据上面的计算结果对目标函数进行归一化，公式为：
对于租房优化问题，归一化后每个个体的目标函数取值如下：
这样，就可以把每个个体的目标函数都归一化到[0,1]的区间。
3.2 生成参考点
2.2节中已经介绍了参考点的含义和作用，下面将介绍如何生成参考点。假设优化目标的数量为M，每个优化目标被划分为p份，则参考点的数量H计算公式如下：
那么，这些参考点的坐标该如何计算呢？假设有一个3目标优化问题，每个优化目标的范围都是[0,1]，将每个优化目标分为4份，参考点求取步骤如下：
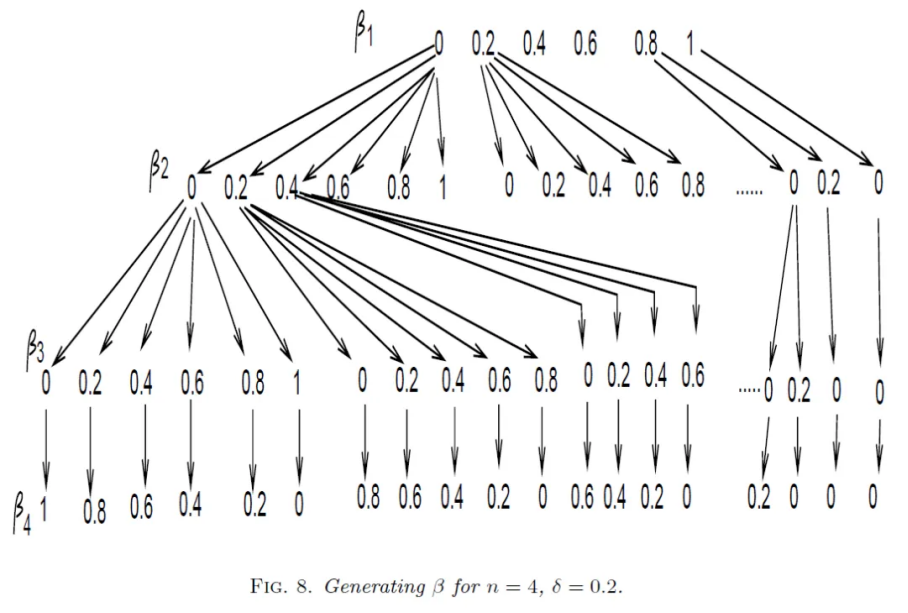
对于4目标优化问题，每个优化目标的范围都是[0,1]，将每个优化目标分为5份，参考点求取步骤如下：
一般性地，对于M目标优化问题，每个优化目标的范围都是[0,1]，将每个优化目标分为p份，参考点求取的matlab代码如下：
function Zr = GenerateReferencePoints(M, p) Zr = GetFixedRowSumIntegerMatrix(M, p)' / p; end function A = GetFixedRowSumIntegerMatrix(M, RowSum) if M < 1 error('M cannot be less than 1.'); end if floor(M) ~= M error('M must be an integer.'); end if M == 1 A = RowSum; return; end A = []; for i = 0:RowSum B = GetFixedRowSumIntegerMatrix(M - 1, RowSum - i); A = [A; i*ones(size(B,1),1) B]; end end使用该代码求解上面几个例子的参考点，结果如下：
3.3 将种群和参考点相关联
计算出参考点之后，还需要建立归一化后的种群与参考点之间的联系。所谓的联系，其实就是将个体和参考点相匹配，确定每个个体究竟属于哪个参考点。前面我们说到，如果参考点分布均匀，NSGA-Ⅲ算法就可以在Pareto前沿上找到尽可能广泛的解。而所谓Pareto前沿，就是将由所有参考点形成的超平面。关联操作的伪代码如下：
从上面的伪代码可知，关联操作的步骤为：绘制参考线→计算个体到参考线的距离→确定个体所属的参考点。具体如下：
1）绘制参考线
将每个参考点和原点相连，形成参考线w。优化问题有M个优化目标，就会有M个参考点，也就会形成M条参考线。
针对上面提到的租房优化问题，我们通过3.1小节已经确定了归一化后的种群目标函数为：(0.4286,0.5385), (0,1), (1,0), (0.6190,0.0769)。
该问题有M个优化目标，假设每个优化目标被划分为2份，则生成的参考点分别为：(1,0), (0.5,0.5), (0,1)。
可以形成三条参考线：
参考线1:x-1=0参考线2:x-y=0参考线3:y-1=02）计算个体到参考线的距离
对于种群中的个体s，计算该个体到每一条参考线的距离。
这其实就是计算点到直线的距离，假设点的坐标为(x1,y1)，直线表达式为：ax+by+c=0，点到直线的距离公式为：
3）确定个体所属的参考点
对于个体s，如果它和第k条参考线的距离最短，那么我们就认为个体s属于第k个参考点，即：
然后，可以求出个体s到该参考线的距离：
重复上述步骤，遍历完所有个体后，就实现了将种群和参考点关联的操作，示意图如下：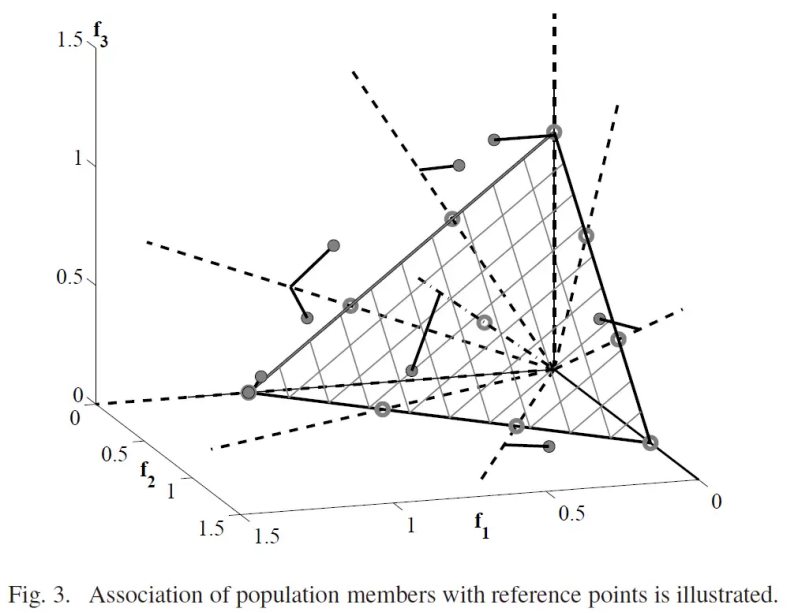
对于上述租房优化问题的个体1，很明显他到第2条参考线的距离最短，因此我们认为个体1属于第2个参考点，同时可以得到该个体和第2条参考线的距离为0.0777。
同理可得个体2属于第3个参考点，距离为0；
个体3属于参考点1，距离为0；
个体4属于参考点1，距离为0.3810。
3.4 小生境保留操作
将种群和参考点关联之后，会出现以下情况：
1）参考点关联一个或多个个体；
2）没有个体与参考点关联。
也就是说，每个参考点所关联的个体数量是不一致的。我们将参考点关联的个体数量定义为参考点的小生境数目ρj。
假设第t代的种群集合为Pt，数量为N，经过交叉变异操作（NSGA-Ⅲ算法交叉变异操作比较常规，这里不再讲解）后得到子代Qt，数量也是N，那么子代和父代组成的集合Rt的数量为2N，选择操作就是需要从Rt中选择N个个体组成t+1代的种群集合Pt+1。
为了得到t+1代的种群集合Pt+1，我们首先按照第一级的非支配水平，确定第一级非支配个体的集合F1，确定需要保留的种群St，然后逐步增加非支配级别，直到St中的种群数量≥N。
假设此时是第l级的非支配水平。如果St中的种群数量=N，那么直接令t+1代的种群集合Pt+1=St即可；
1）确定备选参考点
2）选择参考点关联的个体添加到Pt+1中
3）更新相关参数
3.5 NSGA-Ⅲ算法总结
经过上面的介绍，已经实现了NSGA-Ⅲ算法的全部过程。再次给出伪代码：
步骤1：初始化集合St为空集，初始化i=1；
步骤2：通过交叉变异，得到重组后的子代Qt；
步骤3：令Rt=Pt∪Qt；
步骤4-8：对Rt进行非支配排序，直到St中的种群数量≥N，得到前l级别的非支配个体集合F1-Fl；
步骤9-10：如果St中的种群数量正好等于N，直接将St作为Pt+1即可。
步骤14：对目标函数进行归一化，并得到参考点集合。这部分的详细介绍参考博客3.1小节和3.2小节。
步骤15：将种群和参考点相关联。这部分的详细介绍参考博客3.3小节。
经过上述步骤，便完成了从第t代种群向第t+1代种群更新的操作。
4.NSGA-Ⅲ算法完整代码
NSGA-Ⅲ算法完整的matlab代码可以从下面的链接获取：
第三代非支配排序遗传算法(NSGAⅢ)的原理和matlab实现资源-CSDN文库
如果想要免费获取，也可以下载PlatEmo工具箱，该工具箱里面集成了NSGA-Ⅲ等非常多种优化算法：
GitHub - BIMK/PlatEMO: Evolutionary multi-objective optimization platform