一.二叉树的概念
1.二叉树的基本概念
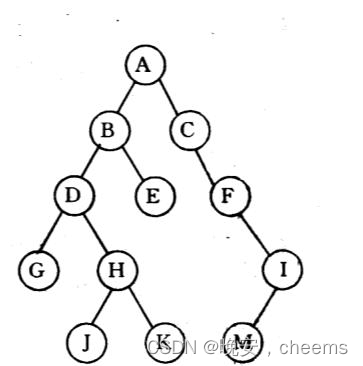
二叉树是一种常见的树状数据结构,它由若干个节点组成,这些节点通过边连接起来。每个节点最多可以有两个子节点,分别称为左子节点和右子节点。
二叉树的特点是每个节点最多有两个子节点,而且左子节点和右子节点的位置是固定的。通常,左子节点小于或等于父节点,右子节点大于父节点,这种顺序被称为二叉搜索树。
二叉树的一个重要概念是根节点,它是树的起始节点,其他节点通过边与根节点相连。根节点没有父节点。另外,每个节点除了子节点的连接外,还可以有一个指向父节点的连接,这样就形成了一个双向连接的二叉树。
2.二叉树的特殊形态
二叉树还有一些常见的特殊形态,例如满二叉树,每个节点要么没有子节点,要么有两个子节点;完全二叉树,除了最后一层之外,其他层的节点都必须是满的,并且最后一层的节点都靠左排列。
3.二叉树的应用
二叉树可以用于许多应用,例如在计算机科学中常用的二叉搜索树可以用来高效地存储和查找数据。二叉树还可以用于表示表达式、文件系统、网络路由等各种问题的结构化表示。
4.二叉树的优缺点
优点:
快速的查找:在二叉搜索树中,由于节点的有序性,可以通过比较节点值的大小来快速定位目标节点,因此查找操作的时间复杂度为 O(log n),其中 n 是树中节点的数量。快速的插入和删除:同样由于二叉搜索树的有序性,插入和删除操作只需要对数级别的操作,因此效率较高。结构简单:相对于其他更复杂的树状数据结构,二叉树的结构相对简单,易于理解和实现。缺点:
可能导致不平衡:如果插入的节点顺序不合适,或者是有序数据的插入顺序,可能会导致二叉树的不平衡,进而影响查找、插入和删除操作的效率,甚至退化为链表。有序性限制:二叉搜索树的有序性要求限制了节点的插入和删除操作,需要保持树的有序性,这增加了对树的平衡性的要求,同时也限制了一些特殊操作的实现。效率不稳定:在最坏的情况下,二叉搜索树的操作时间复杂度可能达到 O(n),其中 n 是树中节点的数量。这种情况通常出现在树的不平衡或有序性不合适的情况下。二.二叉树的功能
二叉树作为一种常见的数据结构,具有以下功能:
查找:二叉搜索树(BST)是一种特殊的二叉树,它的左子节点的值小于等于父节点,右子节点的值大于等于父节点。这种有序性使得在BST中可以高效地进行查找操作。通过比较节点的值,可以快速确定目标节点的位置,从而实现快速查找。
插入和删除:在二叉树中插入和删除节点通常是相对容易的操作。对于BST,插入操作可以根据节点值的大小关系找到合适的位置进行插入。删除操作需要考虑节点的后继或前驱节点,以保持树的有序性。
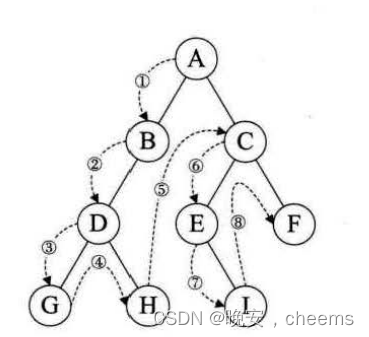
遍历:二叉树的遍历包括三种基本方式:前序遍历、中序遍历和后序遍历。前序遍历先访问根节点,然后递归地遍历左子树和右子树;中序遍历先遍历左子树,然后访问根节点,最后遍历右子树;后序遍历先遍历左子树和右子树,最后访问根节点。
最值查找:通过遍历二叉树,可以找到树中的最小值和最大值。在二叉搜索树中,最小值一定在最左边的叶子节点,最大值一定在最右边的叶子节点。
平衡性检查和调整:二叉树的平衡性对于保持操作的效率非常重要。当二叉树不平衡时,可以进行相应的调整操作,如旋转、重建等,使得树保持平衡状态。
应用领域:二叉树可以用于解决各种问题,例如表达式求值、排序算法(如快速排序中的划分操作)、哈夫曼编码、文件系统的组织结构、数据库索引等。它们提供了一种结构化的方式来组织和操作数据。
三.二叉树的代码实现
1.创建二叉树的结构体
struct TreeNode 是用来定义二叉树结点的结构体。它包含以下几个成员:
val:存储结点的值。这个成员变量可以根据实际需要定义为任意类型,这里定义为 int 类型。
left:指向当前结点的左子树的指针。它是一个指针类型,指向另一个 struct TreeNode 结构体,用于表示左子树。
right:指向当前结点的右子树的指针。它也是一个指针类型,指向另一个 struct TreeNode 结构体,用于表示右子树。
通过这样的结构体定义,可以创建二叉树的结点,并通过 left 和 right 指针将这些结点连接起来,形成一个完整的二叉树数据结构。在二叉树的操作中,通过访问结点的 val 成员可以获取结点的值,通过访问 left 和 right 指针可以获取左子树和右子树的结点。这样的结构体定义提供了一种组织和访问二叉树的方式。
// 二叉树结点的定义struct TreeNode {int val;struct TreeNode* left;struct TreeNode* right;};2.创建新结点
createNode(int val):创建新结点
val:要存储在新结点中的值。返回值:指向新创建结点的指针。 // 创建新结点struct TreeNode* createNode(int val) { struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode)); newNode->val = val; newNode->left = NULL; newNode->right = NULL; return newNode;}3.插入结点
insertNode(struct TreeNode* root, int val):
val:要插入的值。root:指向二叉树的根结点的指针。返回值:指向更新后的二叉树根结点的指针。运行原理:根据二叉搜索树的性质,如果要插入的值小于当前结点的值,则将其插入到左子树中;如果要插入的值大于等于当前结点的值,则将其插入到右子树中。递归地在合适的子树上调用插入函数,直到找到合适的位置插入新结点。 // 插入结点struct TreeNode* insertNode(struct TreeNode* root, int val) { if (root == NULL) { return createNode(val); } if (val < root->val) { root->left = insertNode(root->left, val); } else { root->right = insertNode(root->right, val); } return root;}4.前序遍历
preorderTraversal(struct TreeNode* root):
root:指向二叉树根结点的指针。返回值:无。运行原理:递归地进行前序遍历,首先输出当前结点的值,然后先递归遍历左子树,再递归遍历右子树。 // 前序遍历void preorderTraversal(struct TreeNode* root) { if (root != NULL) { printf("%d ", root->val); preorderTraversal(root->left); preorderTraversal(root->right); }}四.二叉树的源码呈现
#include <stdio.h>#include <stdlib.h>// 二叉树结点的定义struct TreeNode { int val; struct TreeNode* left; struct TreeNode* right;};// 创建新结点struct TreeNode* createNode(int val) { struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode)); newNode->val = val; newNode->left = NULL; newNode->right = NULL; return newNode;}// 插入结点struct TreeNode* insertNode(struct TreeNode* root, int val) { if (root == NULL) { return createNode(val); } if (val < root->val) { root->left = insertNode(root->left, val); } else { root->right = insertNode(root->right, val); } return root;}// 前序遍历void preorderTraversal(struct TreeNode* root) { if (root != NULL) { printf("%d ", root->val); preorderTraversal(root->left); preorderTraversal(root->right); }}int main() { struct TreeNode* root = NULL; root = insertNode(root, 5); insertNode(root, 3); insertNode(root, 8); insertNode(root, 2); insertNode(root, 4); insertNode(root, 7); insertNode(root, 9); printf("Preorder traversal: "); preorderTraversal(root); return 0;}