一.堆排序的概念
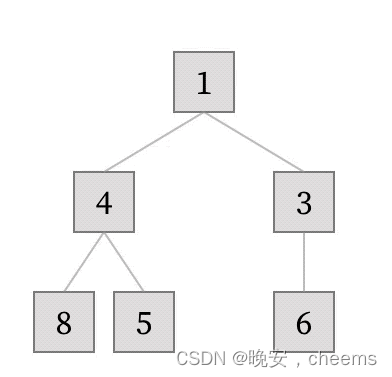
1.堆的思想
堆排序是一种常见的排序算法。它的基本思想是:
将待排序序列构建成一个大顶堆。大顶堆的特点是根节点的值大于或等于其左右子节点的值。
交换根节点(即当前最大值)与末尾元素。
减小堆的规模,重新调整结构,使其满足堆定义,然后再次交换根节点与当前末尾元素。
反复执行步骤2和步骤3,直到整个序列有序。
2.堆的实现步骤
具体实现步骤如下:
建立大顶堆:从最后一个非叶子节点开始调整,向上直到根节点。交换堆顶元素(即当前最大值)与末尾元素,并减小堆的规模。重新调整堆,使其满足堆定义。重复步骤2和步骤3,直到整个序列有序。堆排序的时间复杂度为O(nlogn)。空间复杂度为O(1),因为它在原数组上进行排序,不需要额外的内存空间。
堆排序的优势是能够在一个数组上就地完成排序,不需要额外的空间。缺点是对于小规模的数据,不如简单的插入排序和冒泡排序快。
3.堆的优点
优点:
时间复杂度为O(nlogn),是比较高效的排序算法之一。在原数组上进行排序,不需要额外的内存空间,即空间复杂度为O(1)。相比于其他基于比较的排序算法,如快速排序和归并排序,堆排序能够避免最坏情况下的性能下降。堆排序算法的关键操作是堆的构建和堆的调整,可以利用堆这种数据结构的性质来快速完成排序。堆排序算法的实现相对简单,容易编码实现。4.堆的缺点
缺点:
对于小规模的数据,堆排序并不一定是最优选择,因为相比于简单的插入排序和冒泡排序,堆排序有较大的常数时间因子。堆排序算法不是原地排序,需要利用原始数组的空间来存储中间结果。在某些情况下,堆排序的性能可能不如其他算法,如快速排序和归并排序。这取决于输入数据的特点。堆排序算法需要利用堆这种特殊的数据结构,对程序员的要求相对较高,实现起来也相对复杂一些。二.堆排序的功能
堆排序的主要功能是对一个给定的数组进行升序或降序排序。具体来说,堆排序有以下几个主要功能:
1.构建大顶堆或小顶堆
堆排序算法首先需要将输入数组构建成一个大顶堆或小顶堆。大顶堆的根节点是数组中的最大值,左右子节点都小于根节点。小顶堆的根节点是数组中的最小值,左右子节点都大于根节点。构建堆的过程使用"heapify"操作,从最后一个非叶子节点开始,逐级向上调整节点位置,直到根节点满足堆的性质。这一步保证了数组中的元素满足堆的特性,为后续的排序奠定基础。2.排序
在构建好堆之后,堆排序会进行反复的交换和调整操作。首先将堆顶元素(即最大值或最小值)与堆的最后一个元素交换位置。然后对新的根节点进行调整,使其满足堆的性质,成为一个新的有效堆。通过不断重复这样的交换和调整过程,可以将最大值或最小值逐步放置到数组的后部,达到排序的目的。这一步通过不断"弹出"堆顶元素并调整堆,最终实现了整个数组的排序。3.支持原位排序
堆排序是一种原地排序算法,不需要额外的内存空间来辅助排序。算法直接在原数组上进行操作,交换和调整元素位置,不需要申请新的数组空间。这使得堆排序的空间复杂度非常低,仅需O(1)的额外空间开销。原地排序的特性使得堆排序可以高效地处理大规模数据,不会受到内存限制的影响。4.时间复杂度优秀
堆排序的时间复杂度为O(nlogn),其中n是输入数组的大小。这是一个非常优秀的时间复杂度,使堆排序成为高效的通用排序算法之一。无论数据规模大小,堆排序的时间复杂度都保持稳定,不会随数据规模的增加而急剧增长。5.适用于大规模数据
由于时间复杂度优秀,堆排序特别适用于排序大规模数据集。相比于一些时间复杂度为O(n^2)的排序算法,堆排序可以更高效地处理海量数据。这使得堆排序在处理大型数据库、大文件排序等场景下具有很强的优势和应用价值。三.堆排序的代码实现
1.构建大顶堆
heapify(arr, n, i) 函数用于构建大顶堆。它从最后一个非叶子节点开始,向上调整整个堆。
heapify(int arr[], int n, int i) 函数:
i 为根节点的子树,使其满足大顶堆的性质。首先找到根节点、左子节点和右子节点中的最大值的下标 largest。如果最大值不是根节点,则将根节点与最大值交换,并递归地调整子树。 void heap_sort(int arr[], int n) { // 构建大顶堆 for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // 交换堆顶元素与末尾元素, 并重新调整堆 for (int i = n - 1; i > 0; i--) { int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; heapify(arr, i, 0); }}
2.堆排序的算法
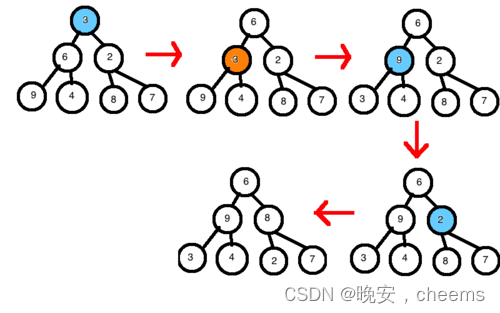
heap_sort(arr, n) 函数实现了堆排序的算法。它首先构建大顶堆,然后反复交换堆顶元素和末尾元素,并重新调整堆。
heap_sort(int arr[], int n) 函数:
heapify 函数,构建一个大顶堆。然后进行交换和调整的循环: 将堆顶元素(即最大值)与数组的最后一个元素交换。对新的根节点调用 heapify 函数,以维护堆的性质。重复这个过程,直到整个数组有序。 void heapify(int arr[], int n, int i) { int largest = i; int left = 2 * i + 1; int right = 2 * i + 2; // 如果左子节点大于根节点 if (left < n && arr[left] > arr[largest]) largest = left; // 如果右子节点大于根节点 if (right < n && arr[right] > arr[largest]) largest = right; // 如果最大值不是根节点 if (largest != i) { // 交换根节点和最大值 int temp = arr[i]; arr[i] = arr[largest]; arr[largest] = temp; // 递归调整子树 heapify(arr, n, largest); }}3.列举例子
main() 函数:
main 函数中,首先定义了一个待排序的数组 data。然后调用 heap_sort 函数对数组进行排序。最后打印排序后的数组。 int main() {int data[] = {12, 11, 13, 5, 6, 7};int n = sizeof(data) / sizeof(data[0]);heap_sort(data, n);printf("Sorted array is \n");for (int i = 0; i < n; i++) printf("%d ", data[i]);printf("\n");return 0;}四.堆排序的源码呈现
#include <stdio.h>void heapify(int arr[], int n, int i) { int largest = i; int left = 2 * i + 1; int right = 2 * i + 2; // 如果左子节点大于根节点 if (left < n && arr[left] > arr[largest]) largest = left; // 如果右子节点大于根节点 if (right < n && arr[right] > arr[largest]) largest = right; // 如果最大值不是根节点 if (largest != i) { // 交换根节点和最大值 int temp = arr[i]; arr[i] = arr[largest]; arr[largest] = temp; // 递归调整子树 heapify(arr, n, largest); }}void heap_sort(int arr[], int n) { // 构建大顶堆 for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // 交换堆顶元素与末尾元素, 并重新调整堆 for (int i = n - 1; i > 0; i--) { int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; heapify(arr, i, 0); }}int main() { int data[] = {12, 11, 13, 5, 6, 7}; int n = sizeof(data) / sizeof(data[0]); heap_sort(data, n); printf("Sorted array is \n"); for (int i = 0; i < n; i++) printf("%d ", data[i]); printf("\n"); return 0;}