1、GBDT简介
GBDT,全称Gradient Boosting Decision Tree,梯度提升树。是集成学习中boosting中较著名的算
法。主要包含两部分:Gradient Boosting 和 Decision Tree。
2、Decision Tree:CART回归树。
(1)什么是CART?
CART全称是Classification and Regression Tree,一种著名的决策树学习算法,分类和回归任务
都可用。GBDT中使用的是CART回归树。
CART回归树算法详解参考:决策树--CART回归树算法详解-CSDN博客。
(2)为什么不用CART分类树?
原因 ①:无论是回归问题还是分类问题,GBDT需要将多个弱分类器的结果累加起来(Boosting的
训练是串行的,一个接一个,每一棵树的训练都依赖于之前的残差。对于Boosting我们应该要求
和)。
原因 ②:且每次迭代要拟合的是梯度值,是连续值所以要用回归树,也就是说DT独指Regression
Decision Tree。
(3)回归树最佳划分点的判别标准?
分类树:熵或者基尼系数最小。
回归树:平方误差最小。
3、Gradient Boosting:拟合负梯度
(1)梯度下降(Gradient Descent)
梯度下降实际是沿梯度相反的方向寻找使目标函数最小时候的参数值。因为一个函数的梯度方向是
函数上升最快的方向,负梯度方向是函数下降最快的方向。
(2)基于残差的训练(boosting的一种训练方式)
每一个后续的模型都会去把前一个模型没有拟合好的残差重新拟合一下。用下一个弱分类器去拟合
当前残差(真实值-当前预测值),之后所有弱分类器的结果相加等于预测值。
(3) 为何Gradient Boosting可以用负梯度近似残差呢?
当损失函数选用MSE时,负梯度<==>残差。
假设我们用MSE做损失函数:
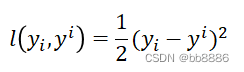
它的负梯度计算公式为:
![]()
4、GBDT
4.1 原理
GBDT,梯度提升决策树,是一种迭代的决策树算法,该算法由多颗决策树组成,所有树的结论累
加起来做最终答案。 如图所示Y = Y1 + Y2 + Y3。
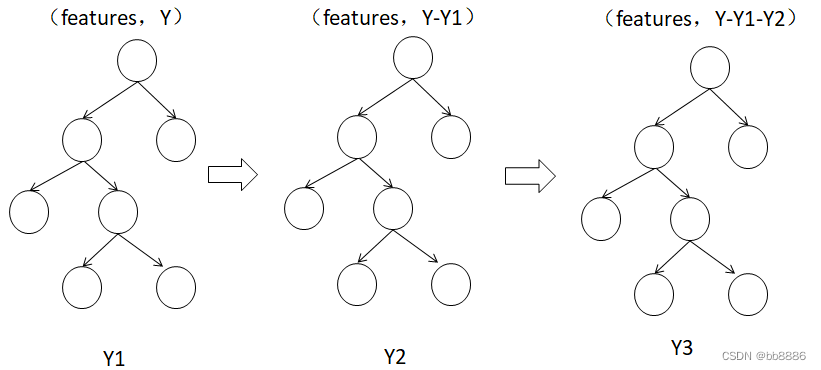
对于Boosting Tree,最后决策时为什么是求和而不是平均?
因为在Bagging里每棵树是独立训练的,互不影响,所以最后决策时需要投票决策。但Boosting的训练是串行的,一个接一个,每一棵树的训练都依赖于之前的残差。所以对于Boosting我们在预测时应该要求和而不是平均。
4.2 GBDT回归任务【例题1】
题目:某人今年30岁了,但计算机或模型GBDT并不知道今年多少岁,那GBDT咋办呢?
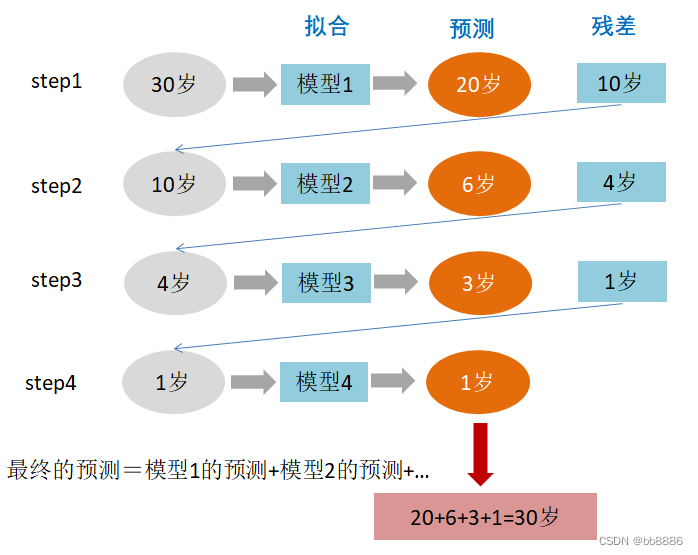
第一步:在第一棵树中,随便用一个年龄(20岁)来拟合,发现误差有10岁(10=30-20);
第二步:在第二棵树中,用6岁去拟合剩下的损失,发现差距还有4岁;
第三步:在第三棵树中,用3岁拟合剩下的差距,发现差距只有1岁了;
第四步:在第四课树中,用1岁拟合剩下的残差,完美。
最终,四棵树的结论加起来,就是真实年龄30岁(实际工程中,gbdt是计算负梯度,用负梯度近似残差)。
4.3 GBDT回归任务【例题2】
题目:假定训练集只有4个人:A,B,C,D,他们的年龄分别是14,16,24,26。其中A、B分别
是高一和高三学生;C,D分别是应届毕业生和工作两年的员工,问题是预测年龄。
传统决策树:
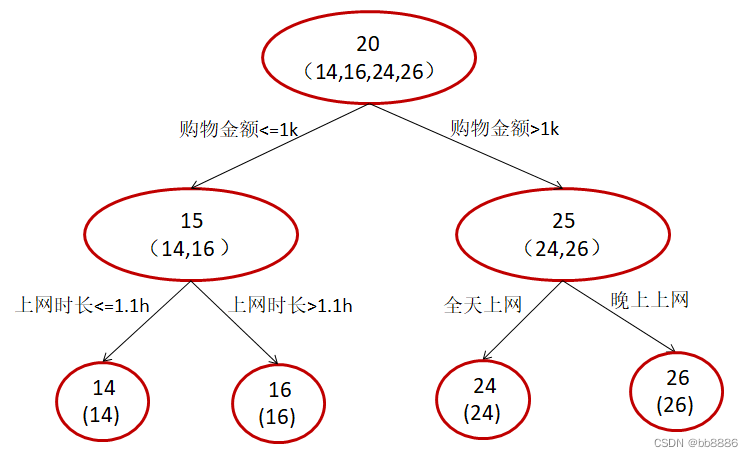
GBDT:限定叶子结点最多两个,限定只学两棵树。

在第一棵树分枝和图1一样,由于A,B年龄较为相近,C,D年龄较为相近,他们被分为左右两
拨,每拨用平均年龄作为预测值。进而得到A,B,C,D的残差分别为-1,1,-1,1。
A: 14岁高一学生,购物较少,经常问学长问题,预测年龄A = 15 – 1 = 14
B: 16岁高三学生,购物较少,经常被学弟问问题,预测年龄B = 15 + 1 = 16
C: 24岁应届毕业生,购物较多,经常问师兄问题,预测年龄C = 25 – 1 = 24
D: 26岁工作两年员工,购物较多,经常被师弟问问题,预测年龄D = 25 + 1 = 26
总结:GBDT需要将多棵树的得分累加得到最终的预测得分,且每一次迭代,都在现有树的基础
上,增加一棵树去拟合前面树的预测结果与真实值之间的残差。
4.4 GBDT分类任务
(1) 缺点
GBDT的分类算法和回归算法没有区别,但由于样本输出不是连续值,而是离散的类别,导致我们
无法直接从输出类别去拟合类别输出的误差。
(2) 解决方式
① 用指数损失函数,此时GBDT退化为Adaboost算法。
② 用类似于逻辑回归的对数似然损失函数的方法(分为二元和多元分类)。
4.5 GBDT与LR的区别
(1) 用图不同
① Logisitic Regression(LR)是分类模型。
② GBDT既可作分类又可回归。
(2) 损失函数不同
① LR的loss是交叉熵。
② GBDT采用回归拟合(将分类问题通过softmax转换为回归问题),用当前损失去拟合实际值与
前一轮模型预测值之间的残差。
(3) 从正则的角度
① LR采用 l1 和 l2 正则;
② GBDT采用弱分类器的个数,也就是迭代轮次T,T的大小影响着算法的复杂度。
(4) 特征组合
① LR是线性模型,具有很好的解释性,很容易并行化,处理亿条训练数据不是问题,但是学习能
力有限,需要大量的特征工程。
② GBDT可以处理线性和非线性的数据,具有天然优势进行特征组合 。