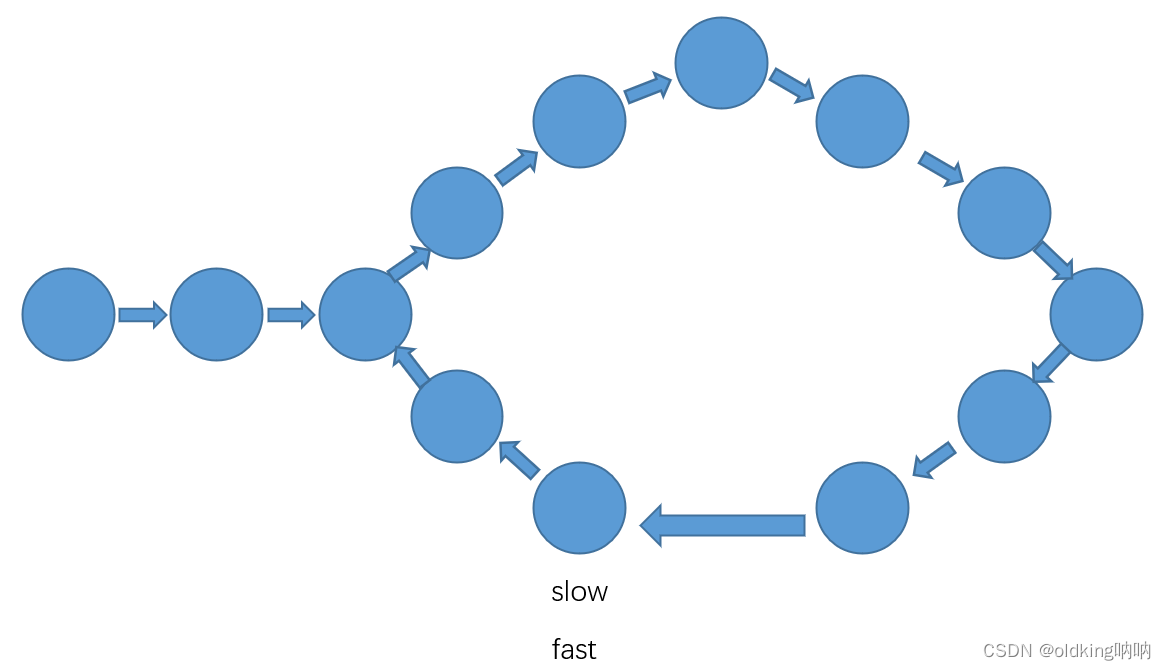
1 题目介绍
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例1:
输入以下这条链,head指向值为3的节点
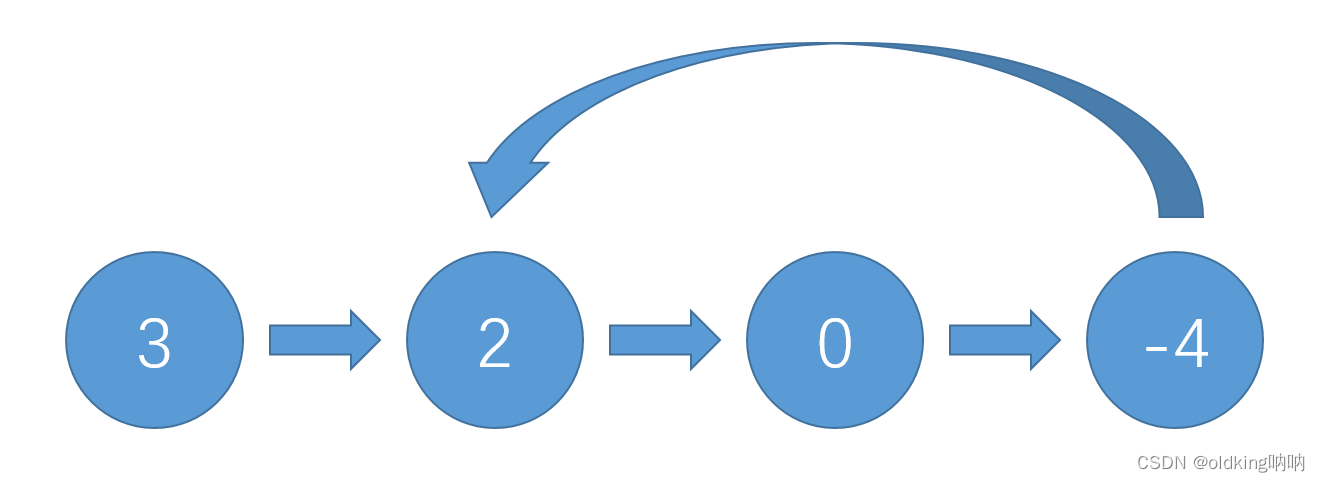
返回值应该为 true
示例2:
输入以下这条链,head指向值为1的节点
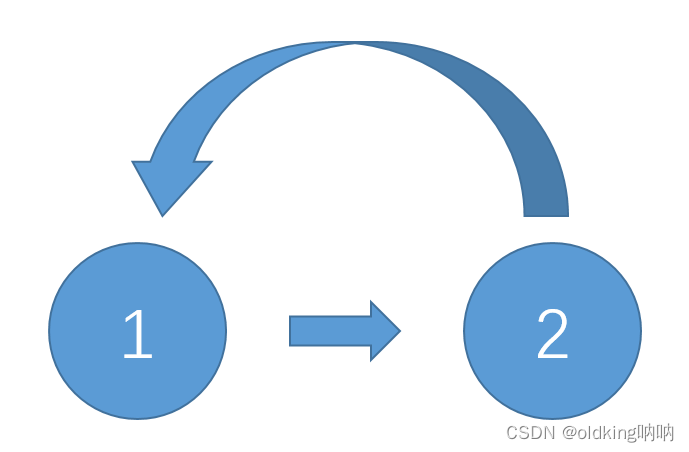
返回值应该为 true
示例3:
输入以下这条链,head指向值为1的节点

返回值应该为false
这里放上链接. - 力扣(LeetCode)
2 解题思路
2.1 思路1(逆序法):
(注意:此方法不是最优解)
基本思想就是逆序整个链表时(简单来说就是让箭头掉头指回上一个节点),如果这个链表是带环的,那么指针cur会从头节点开始遍历,最终回到头节点,若链表不带环,则指针cur回不到头节点
由于有些链表不带头节点,所以一开始需要我们手动创建一个哨兵位
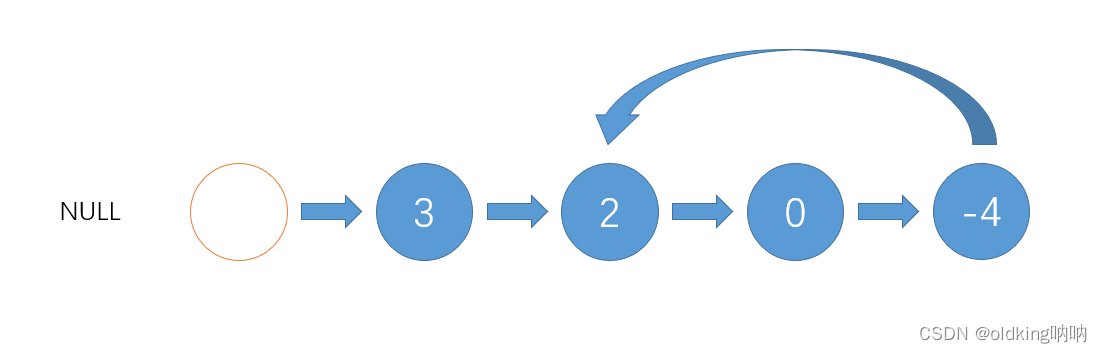
我们需要先定义三个指针,负责将箭头转向
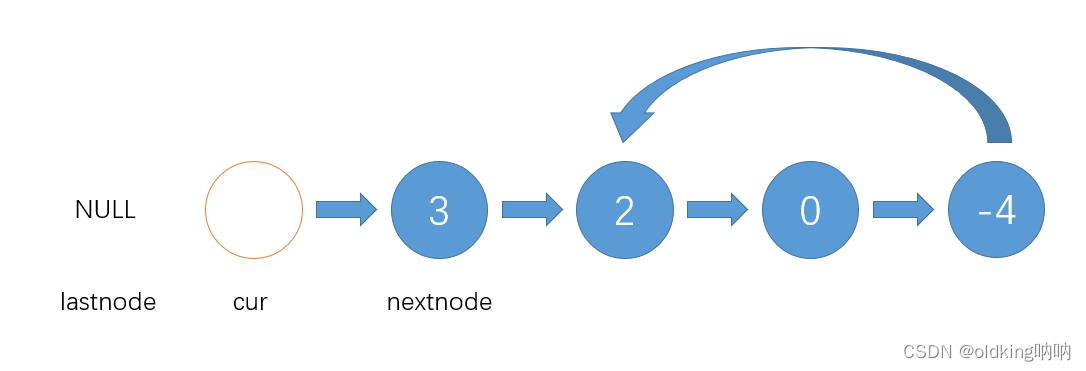
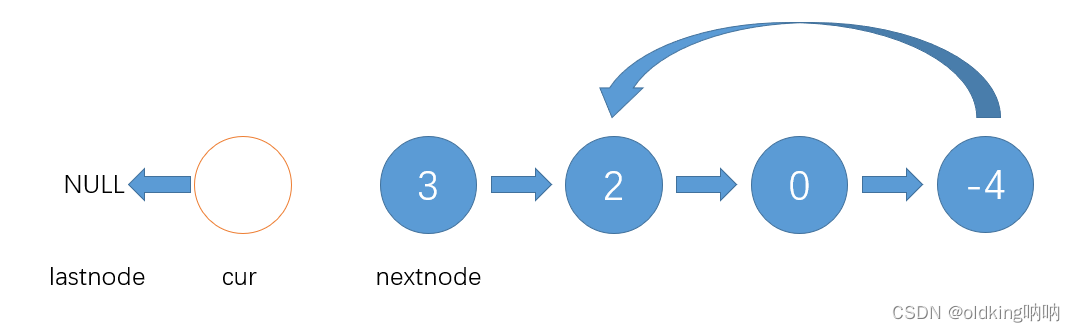
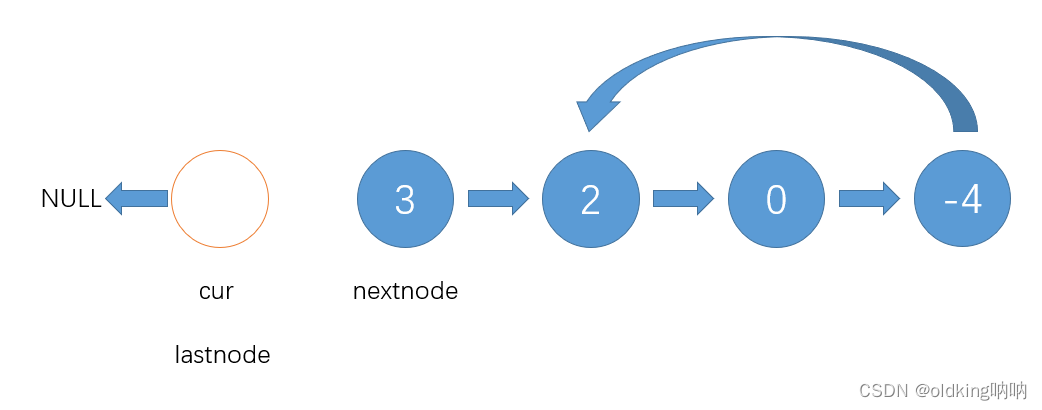
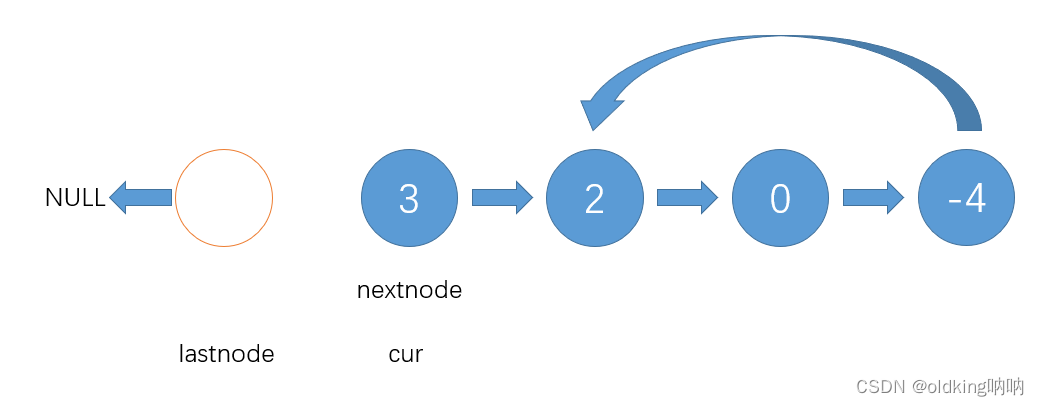
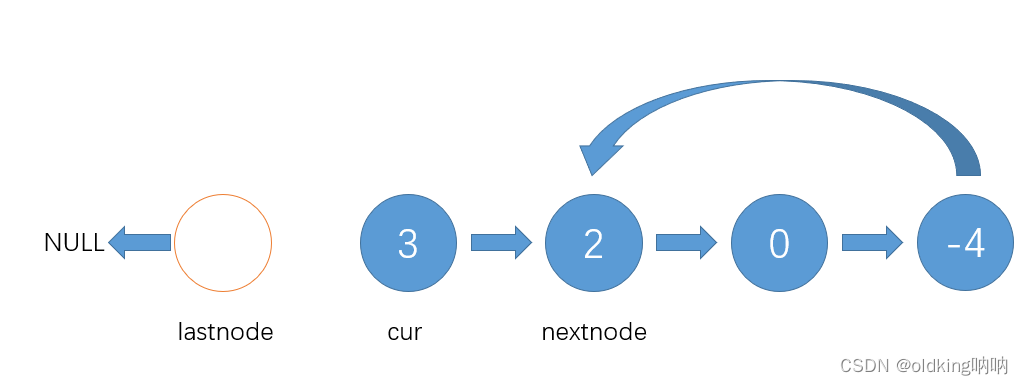 接着就是如法炮制
接着就是如法炮制
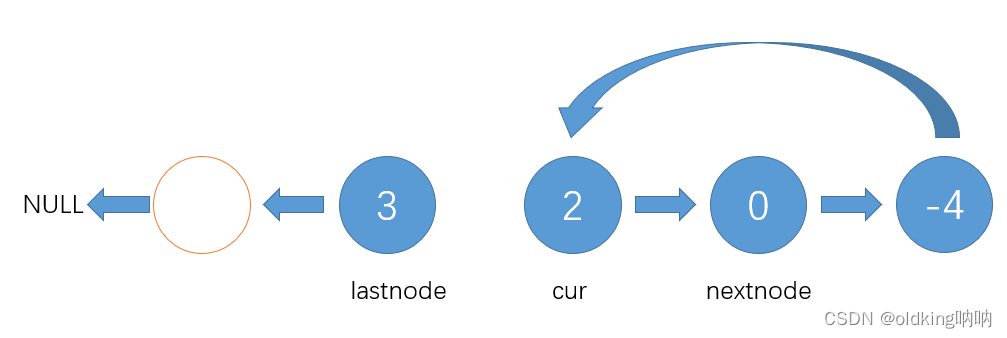
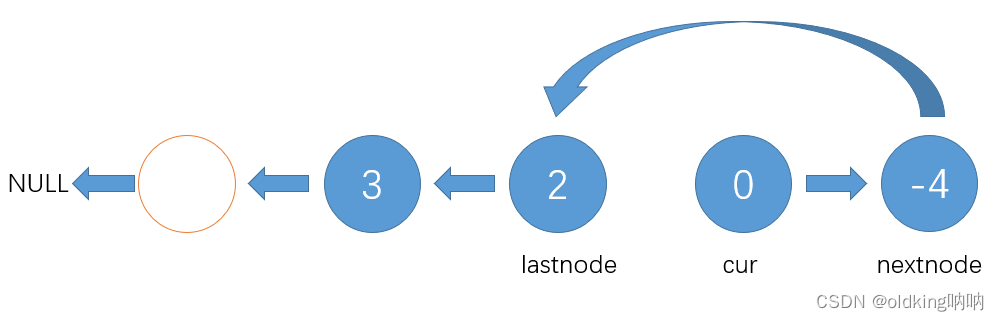
注意,这里nextnode回到了值为2的节点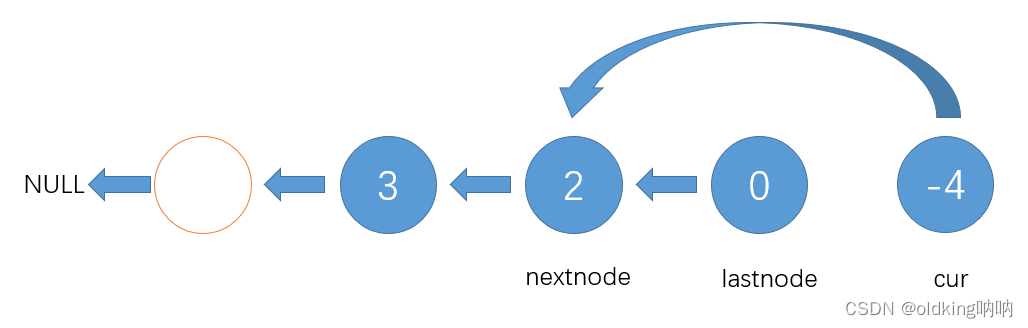
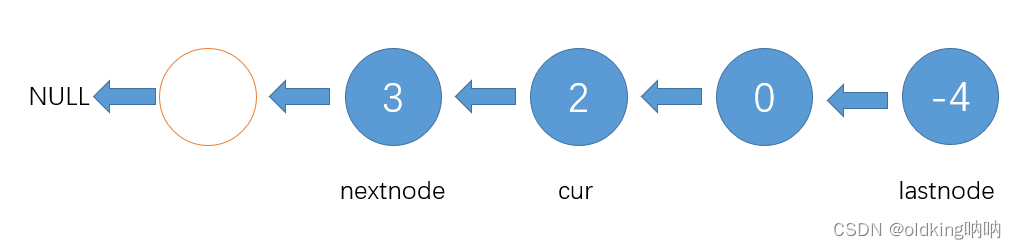
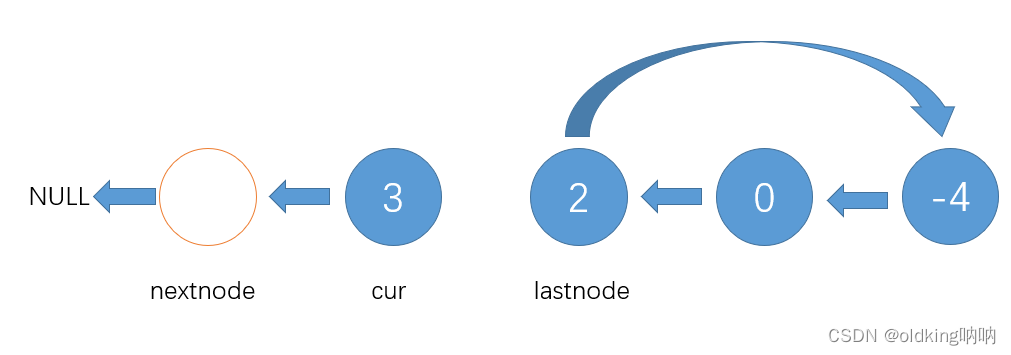
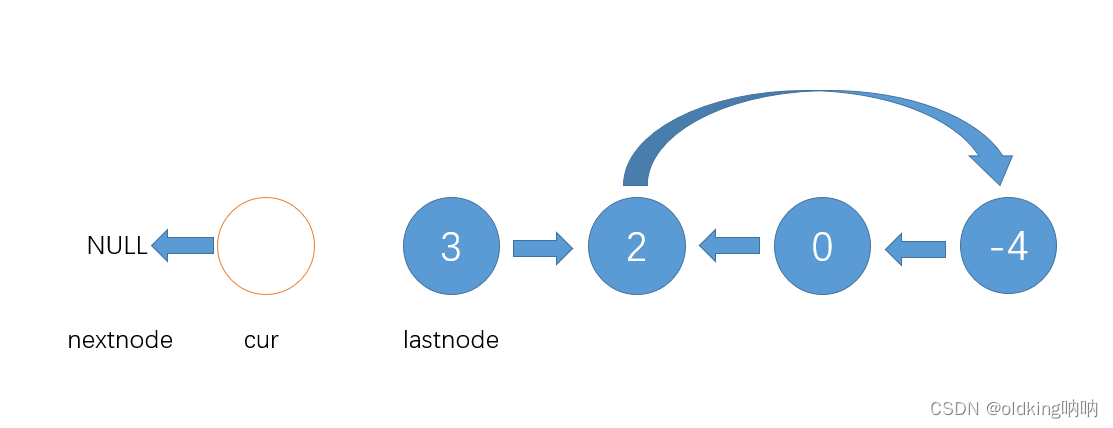
(注意:nextnode指向NULL时,让循环停止,并且开始检测 cur 是否回到了哨兵位,否则就停不下来了)
此时我们发现 cur 回到了哨兵位,一旦产生这种情况,就证明这个链表是带环的
立马返回 ture 就可以
对于不带环的链表来讲,检测到 cur 没有回到哨兵位,就返回 false
2.2 思路2(快慢指针):
基本思路就是快慢指针,一个指针跑得快一点,另一个慢一点,让他俩一直随着 next 指针遍历,快指针和慢指针的距离不断缩短,直到两者相遇,就好比两个人绕操场跑步,都是匀速跑,一个块一个慢,如果不记时间的话那么,这两个人一定会相遇,一旦相遇,就说明这个链表是带环的,因为两者速度不一样,跑道是直线的话是一定不会相遇的
(这个方法是最优解)
快指针:一次走两步(每次走一步都要判断一下 fast 和 fast->next 是否为 NULL,防止出现野指针)
慢指针:一次走一步
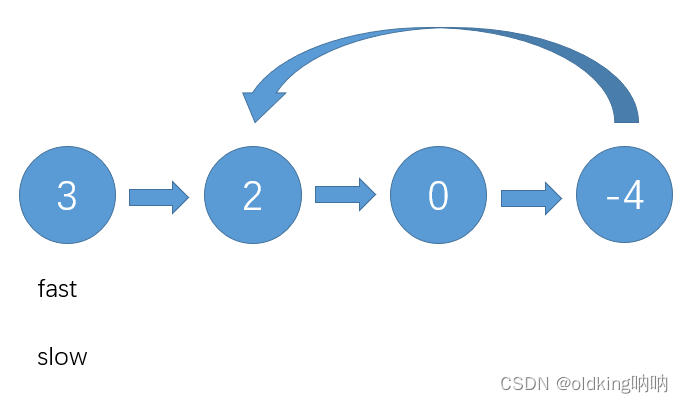
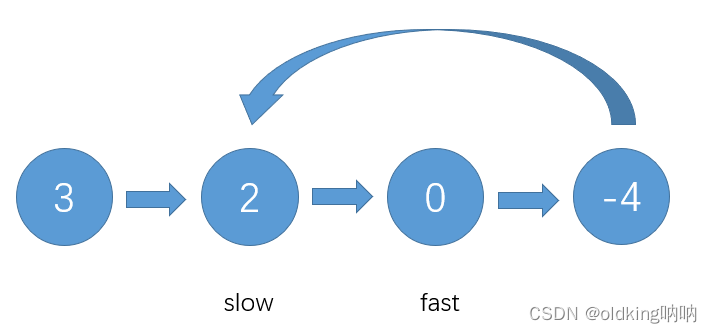
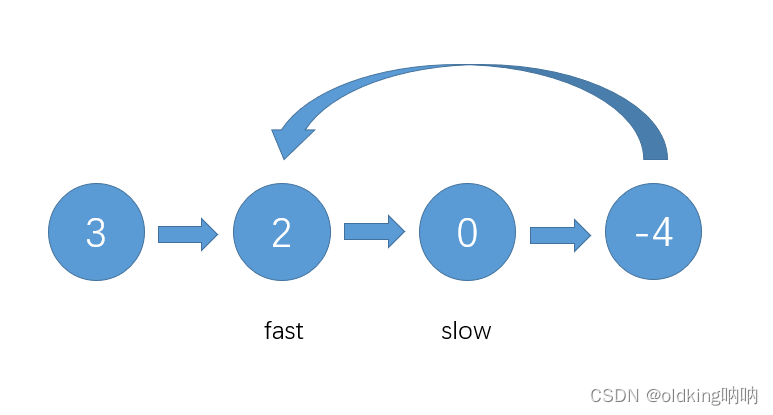
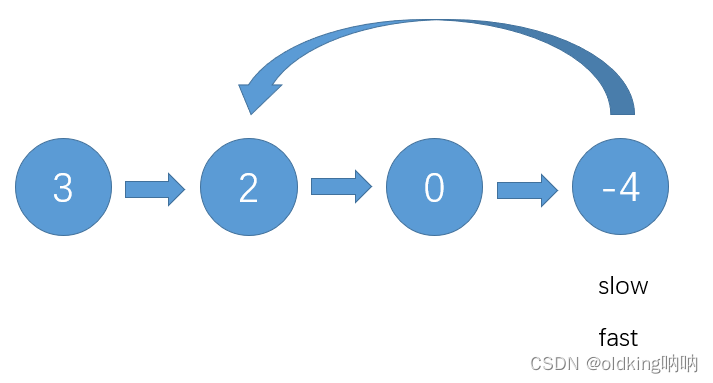
此时发现两者相遇,返回 true
如果 fast 或者 fast->next 在某个时刻 为 NULL,证明这个链表不是带环的,返回 false
3 实现代码
3.1 思路1(逆序法):
typedef struct ListNode ListNode;bool hasCycle(struct ListNode *head) { //输入为空,返回false if(head == NULL) { return false; } //创建头节点 ListNode* headnode = (ListNode*)calloc(1, sizeof(ListNode)); if(headnode == NULL) { perror("hasCycle::calloc"); exit(1); } headnode->next = head; //创建cur,前节点,后节点 ListNode* lastnode = NULL; ListNode* cur = headnode; ListNode* nextnode = headnode->next; //执行逆置 while(nextnode != NULL) { cur->next = lastnode; lastnode = cur; cur = nextnode; nextnode = nextnode->next; } //判断是否是最开始的那个头节点 if(cur == headnode) { return true; } else { return false; }}3.2 思路2(快慢指针):
typedef struct ListNode ListNode;bool hasCycle(struct ListNode *head) { //如果输入为空,或者只有一个节点并且其next也没有指向任何节点 //就判断为非带环节点 if(head == NULL || head->next == NULL) { return false; } //定义快慢指针 ListNode* fast = head; ListNode* slow = head; //快指针碰到NULL就停下 while(fast != NULL && fast->next != NULL) { fast = fast->next->next; slow = slow->next; //如果两者相遇,就一定是带环链表 if(fast == slow) { return true; } } //一旦快指针被迫停下,就证明这个链表一定不带环 return false;}4 衍生思考
4.1 带环链表里快慢指针为什么一定会相遇
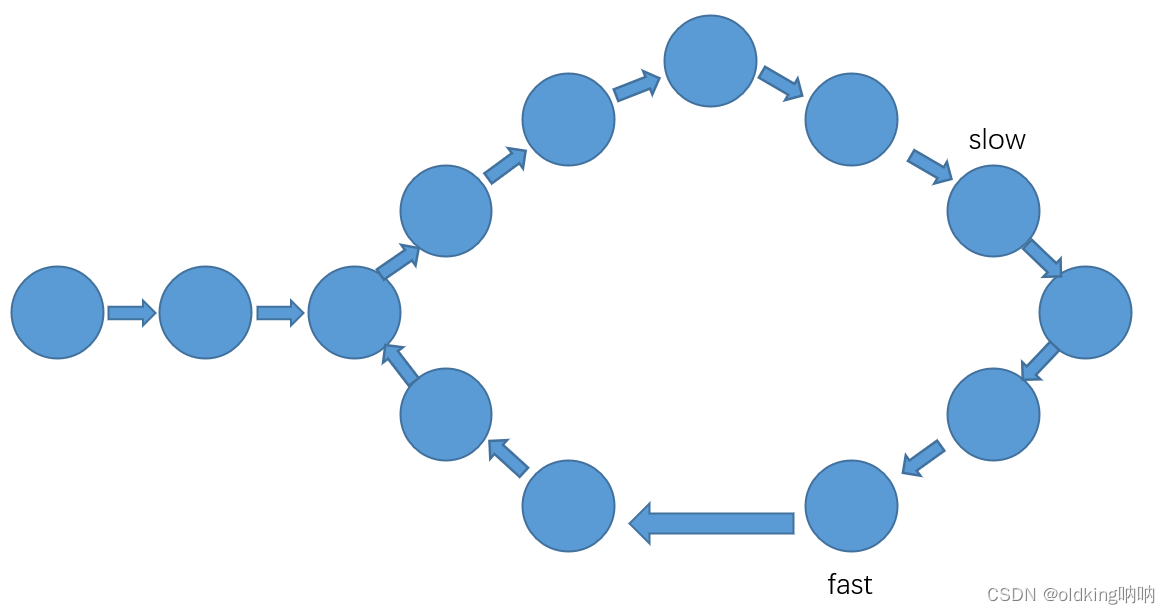
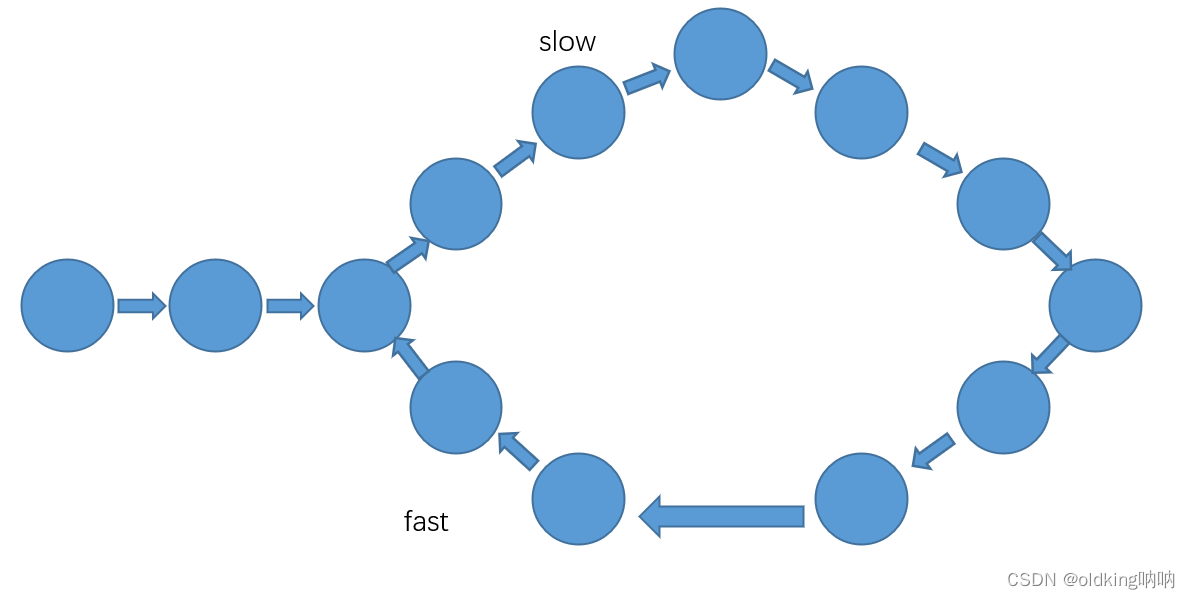
当 slow 进入环的时候,slow 和 fast 就会有距离差了,每一回合之后,fast 和 slow 就会缩短一个节点的距离,直到 fast 和 slow 的距离为0,即相遇为止
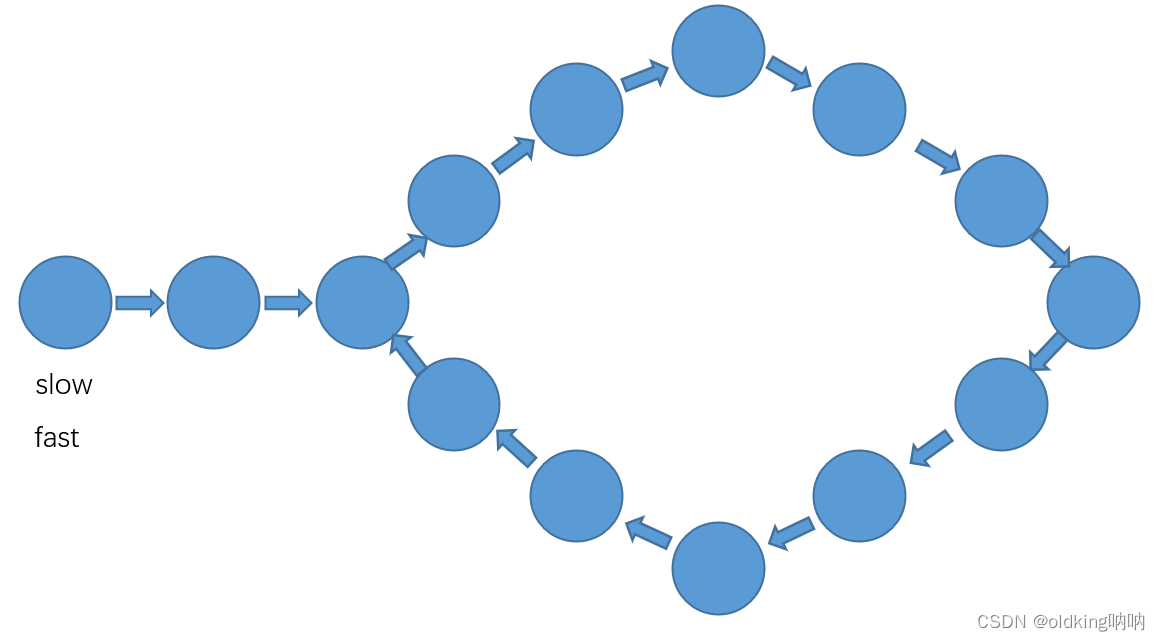
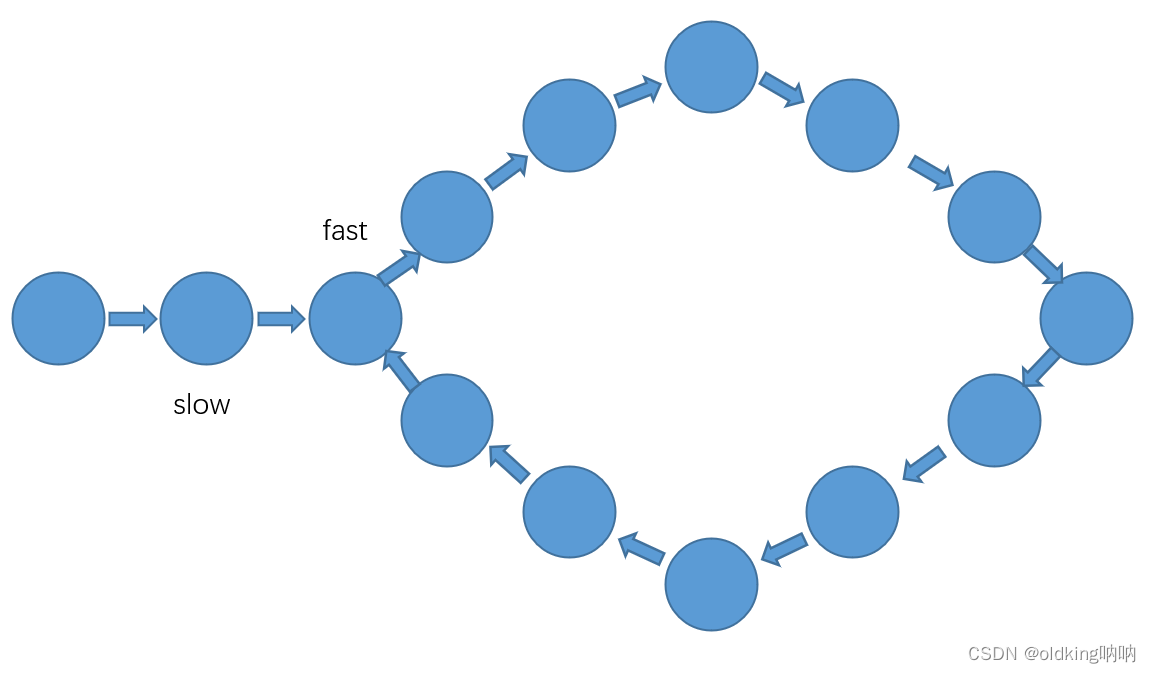
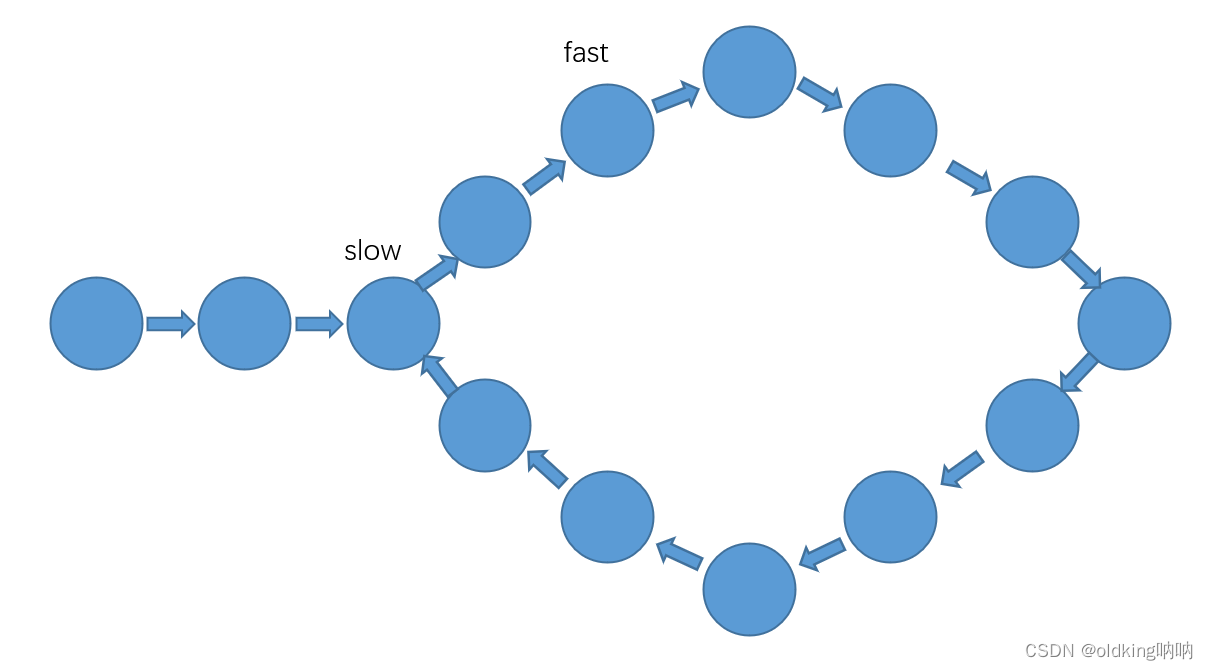
上图这里,fast 和 slow 就相差了10个节点

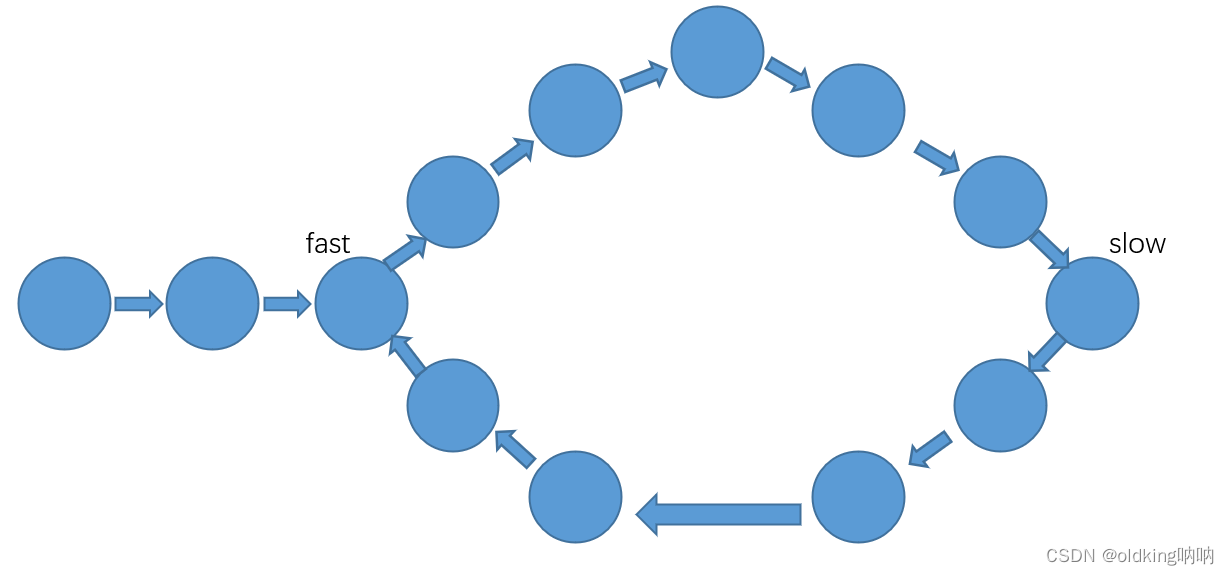
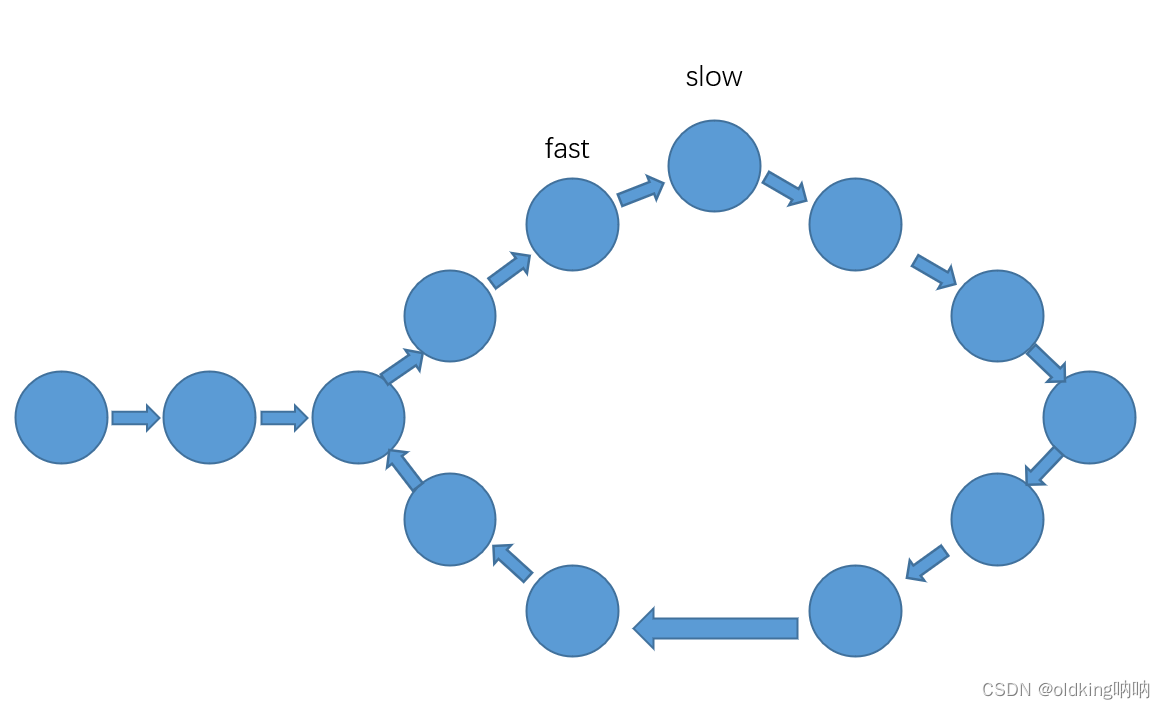
上图这里接着走了一回合,fast 和 slow 的距离就缩短了1变成了9个节点了
所以两者在环里面一定会相遇
4.2 快指针一次跳更多步,两者还会相遇嘛
比方说,快指针一次跳3步,那么每回合两者距离缩短的速度是2,也就是每回合两者距离缩短2,如果两者相距的距离是2的倍数,那么 fast 就会和 slow 相遇,如果二者相距的距离不是2的倍数,即是个奇数,那么快指针一定会在某个回合直接超过 slow 而不会相遇,而此时,你会发现正是因为 fast 越过了 slow,导致两者相距的距离为“奇数 - 1”即偶数了,那此时 fast 和 slow 的相遇就是必定的事了,如果快指针一次跳更多也是一样的道理,如法炮制即可
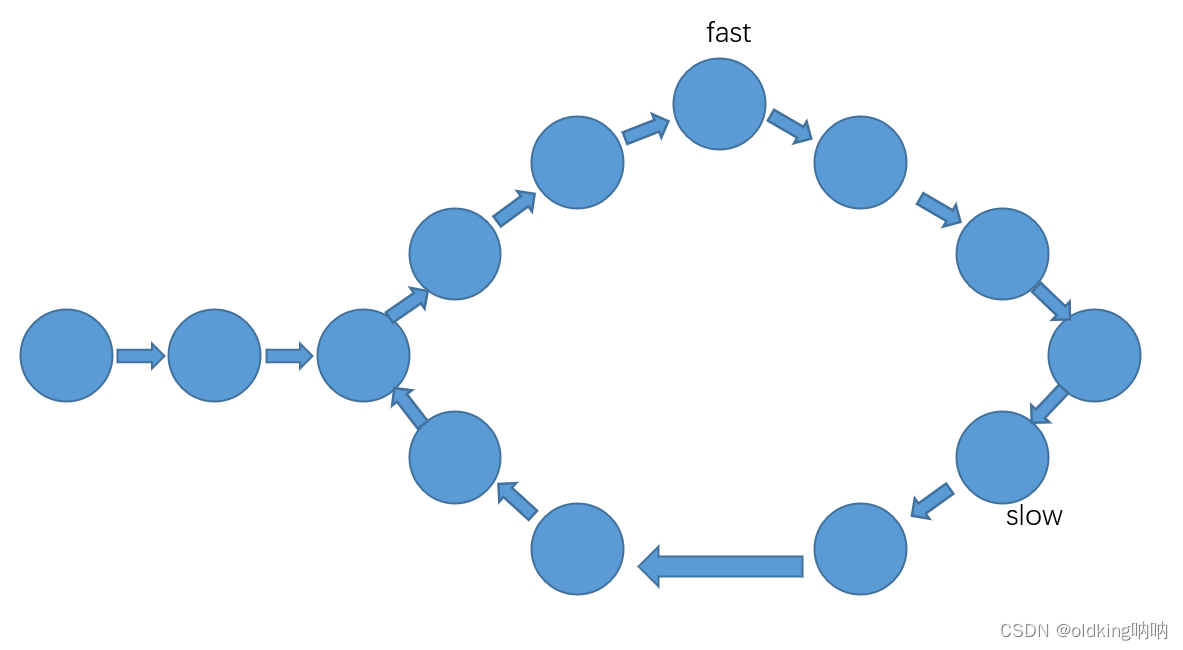
偶数情况:
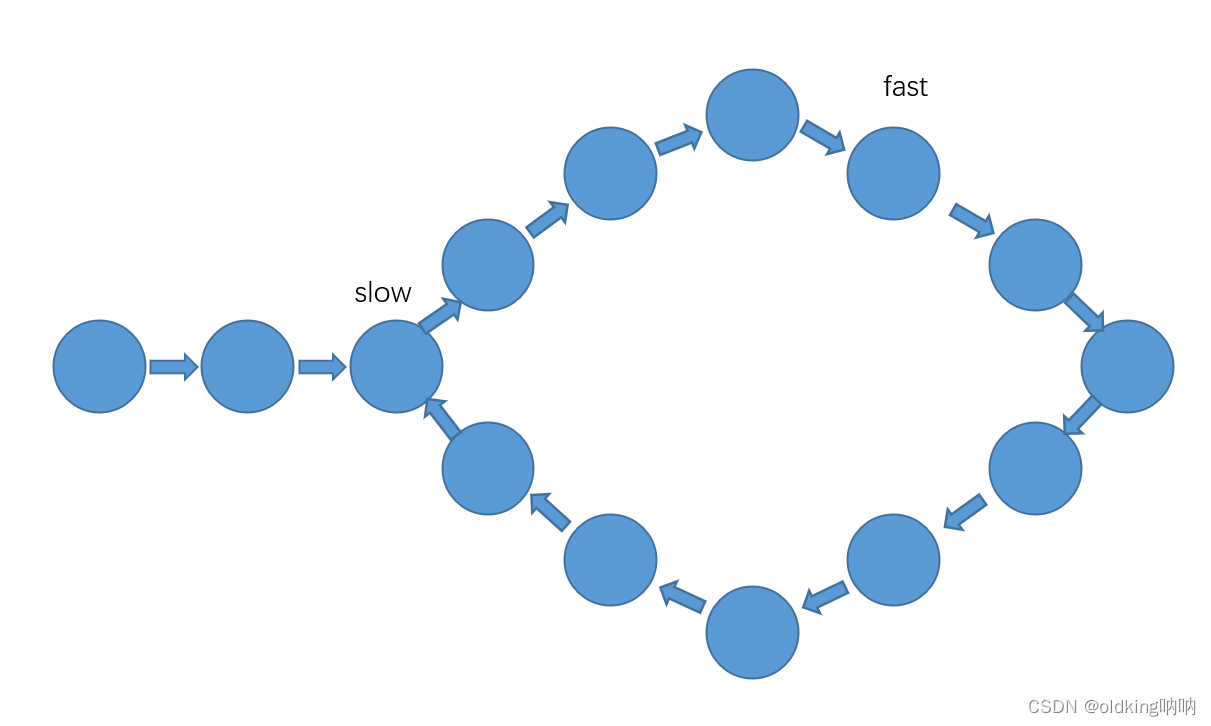
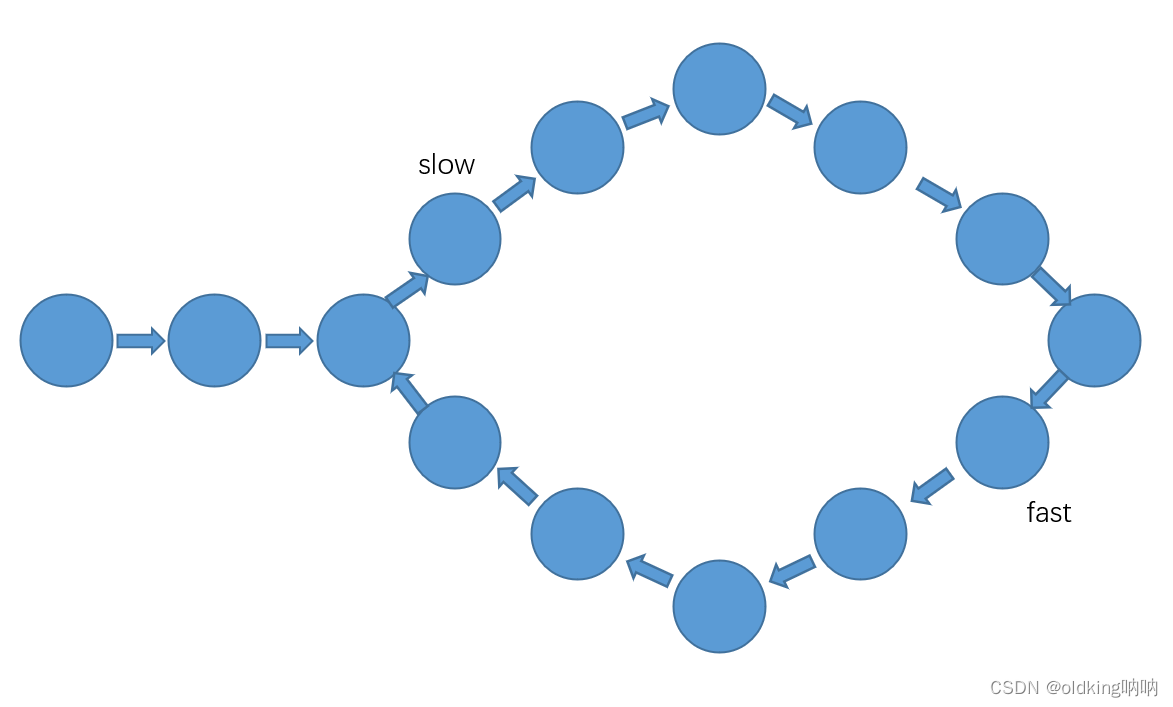
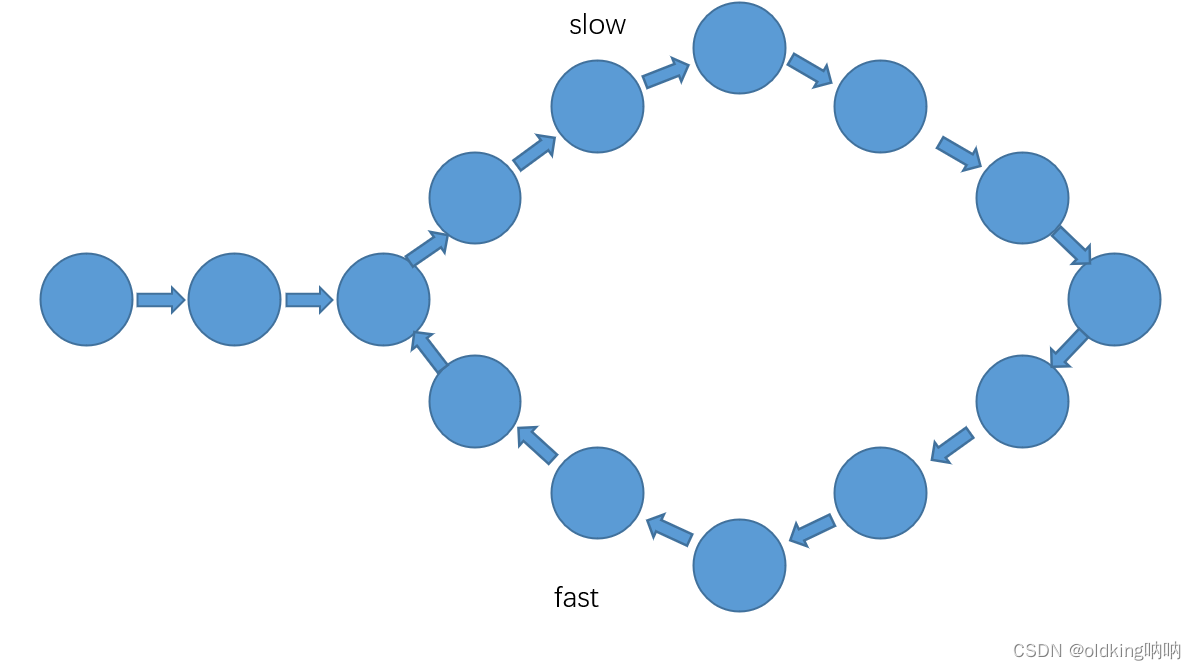

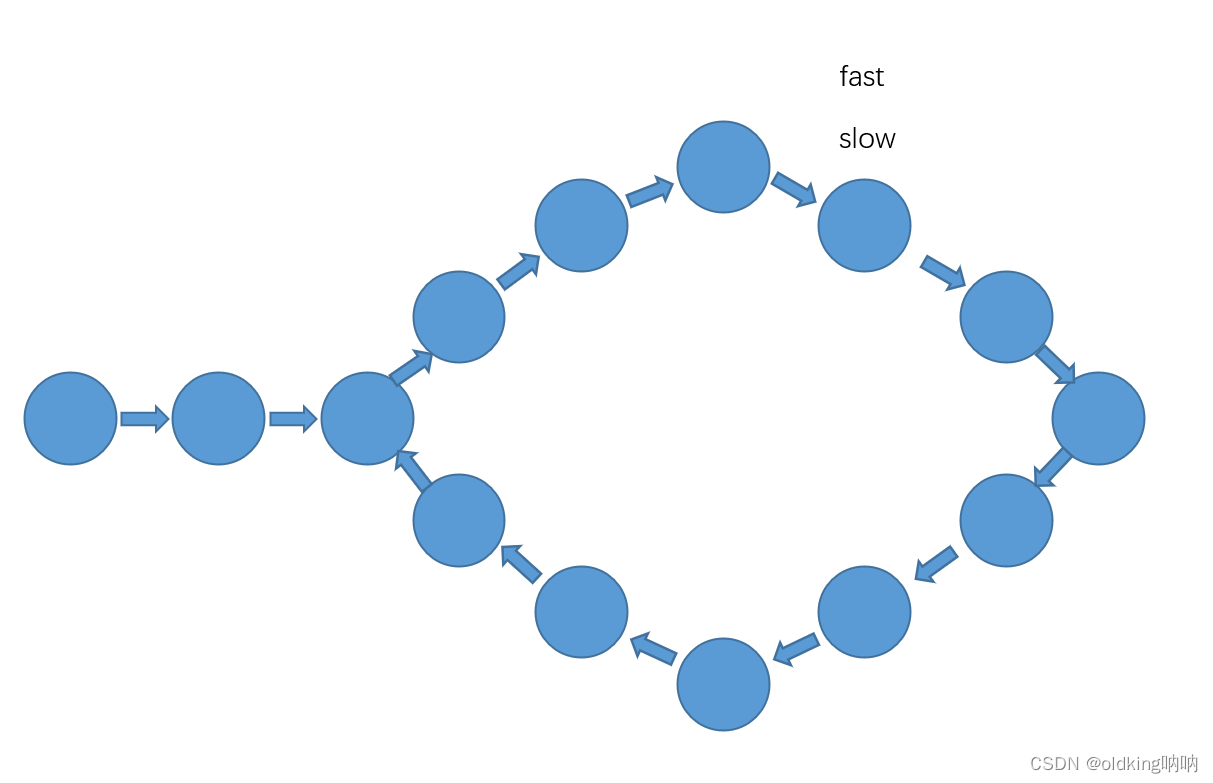
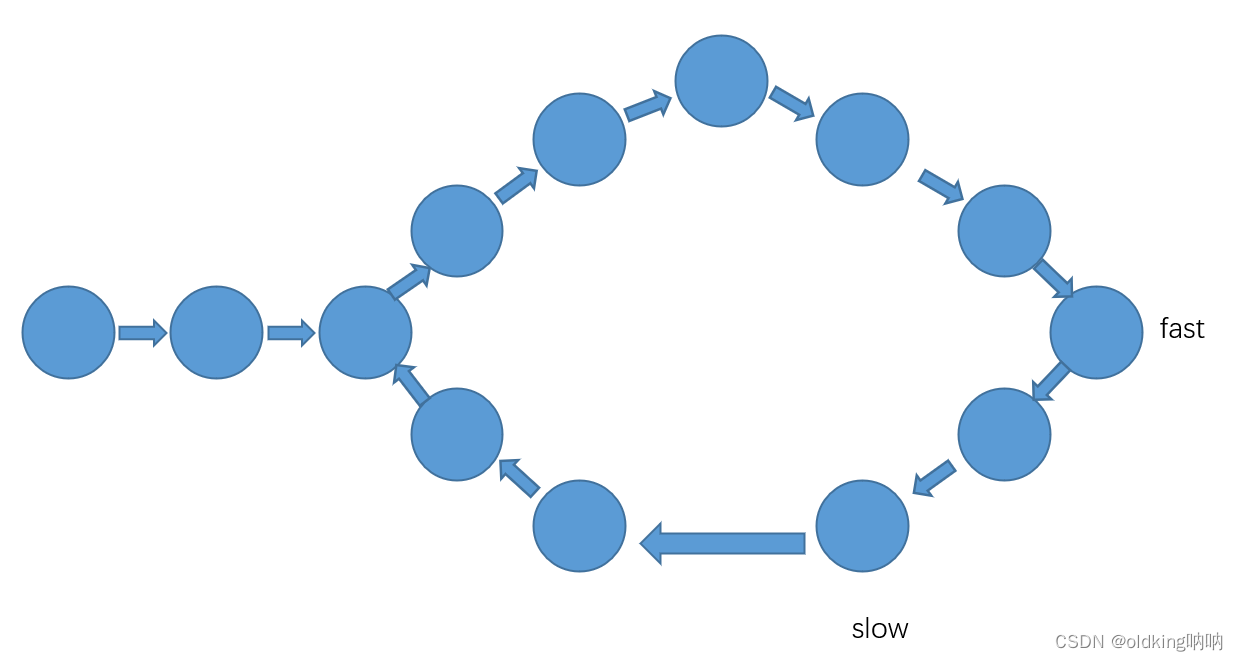
奇数情况:
注意此时这里两者相距 7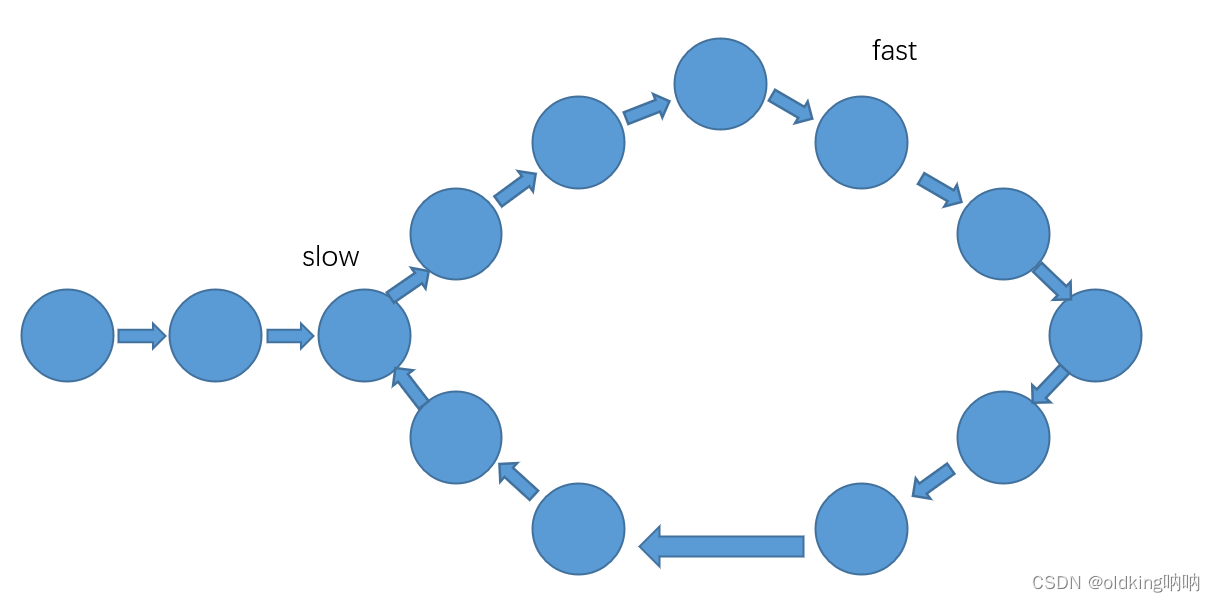
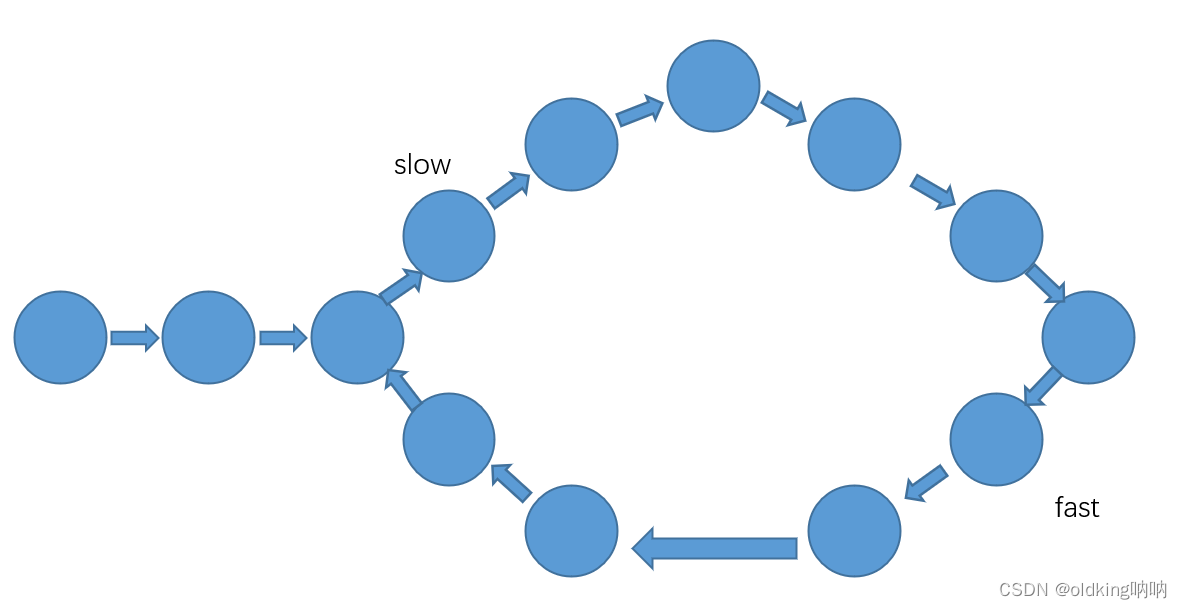
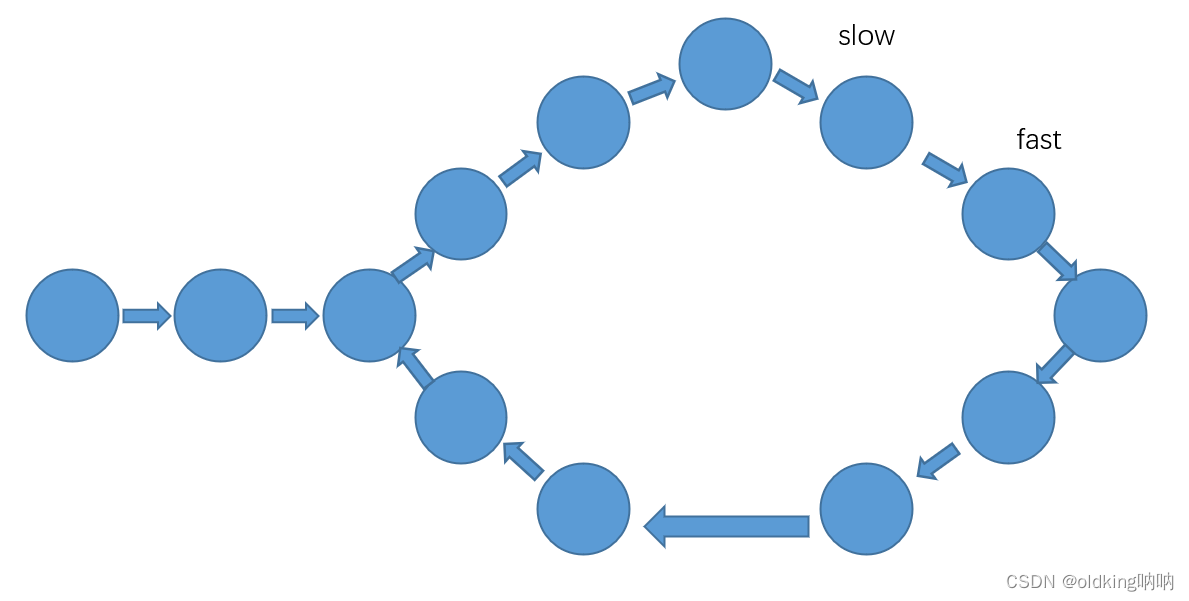
上图这里两者就相距 10 为偶数