很幸运拿了辽宁赛区的省一,进入6月1号的国赛啦...
这篇文章主要对第十五届省赛大学B组(C++)进行一次完整的复盘,这次省赛==2道填空题+6道编程题:
A.握手问题
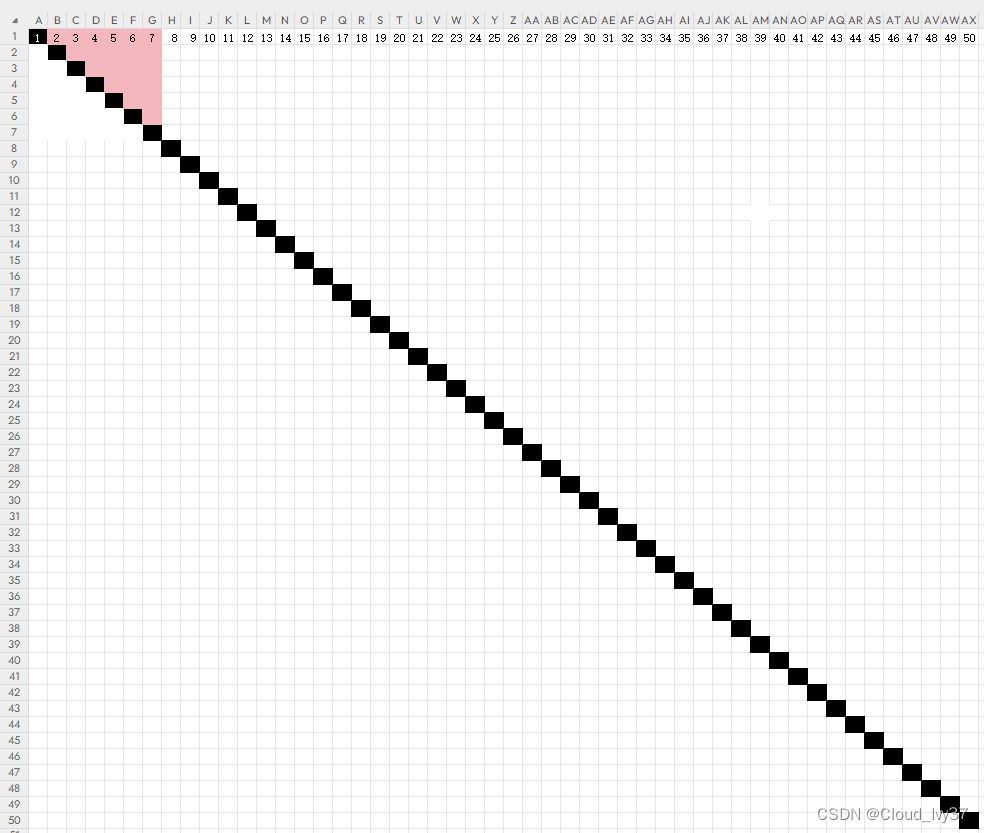
把握手情景看成矩阵:
粉色部分是7个不能互相捂手的情况
由于每个人只能和其他人捂手, 所以黑色情况是不算的
1和2握手==2和1握手,就是只用算一半的对角矩阵
#include<iostream>using namespace std;int main(){ int a=0; for(int i=49;i;i--) a+=i; int b=0; for(int i=6;i;i--) b+=i; int ans=a-b; cout<<ans<<endl;//最后求得答案为1204 return 0;}B.小球反弹
这题考试的时候我是直接跳过的,到最后也没来得及看,看了估计也算不对,haha
整体思路是:
最终返回左上角时,小球走过的水平路程和垂直路程一定是343720和233333的偶数倍
并且水平路程与垂直路程之比一定为15:17
#include<iostream>#include<cmath>using namespace std;typedef long long ll;const int N=1e4;const ll X=343720;const ll Y=233333;int main(){ for(ll x=2;x<=N;x+=2){ for(ll y=2;y<=N;y+=2){ if (15*Y*y==17*X*x){ printf("%lf",sqrt((X*x)*(X*x)+(Y*y)*(Y*y))); //结果是1100325199.770395 return 0; } } }}C.好数
这题暴力枚举就能AC,数据不大,haha
#include<iostream>using namespace std;typedef long long ll;const int N=1e7+5;ll ans;bool check(int x){ int flag=0; while(x>0){ int t=x%10; if(!flag){ if(t%2==0) return false; else flag=1; } else{ if(t%2!=0) return false; else flag=0; } x/=10; } return true;}int main(){ int n; cin>>n; for(int i=1;i<=n;i++) if(check(i)) ans++; cout<<ans<<endl; return 0;}
D.R格式
考试时候的代码:
#include<iostream>#include<cmath>using namespace std;typedef long long ll;int main(){ int n; double d; cin>>n>>d; ll a=(ll)pow(2,n); double ans=a*d; double res=(ll)ans+0.5; if(ans>=res) cout<<(ll)ans+1<<endl; else cout<<(ll)ans<<endl; return 0;}混了一半的分数:
高精度优化(AC):
#include<iostream>#include<algorithm>//reverse函数:前后翻转#include<cstring>//to_string函数:数字常量转化为字符串using namespace std;typedef long long ll;int n;string d;string ans="1";string add(string a,string b){ string res; int la=a.size(),lb=b.size(); int i=la-1,j=lb-1,jw=0; while(i>=0||j>=0){ int sum=jw; if(i>=0) sum+=a[i--]-'0'; if(j>=0) sum+=b[j--]-'0'; jw=sum/10; res+=to_string(sum%10); } if(jw) res+=to_string(jw); reverse(res.begin(),res.end()); return res;}string mul(string a,string b){ string res="0"; int la=a.size(),lb=b.size(); for(int i=la-1;i>=0;i--){ int jw=0; string temp; for(int j=lb-1;j>=0;j--){ int sum=(a[i]-'0')*(b[j]-'0')+jw; jw=sum/10; temp+=to_string(sum%10); } if(jw) temp+=to_string(jw); reverse(temp.begin(),temp.end()); for(int k=0;k<la-1-i;k++) temp+="0"; res=add(res,temp); } return res;}int main(){ cin>>n>>d; while(n--) ans=mul(ans,"2"); string newd="";int flag; for(int i=0;i<d.size();i++){ if(d[i]!='.') newd+=d[i]; else flag=d.size()-i-1; } ans=mul(newd,ans); int key=ans.size()-flag; string s=""; for(int i=0;i<key;i++) s+=ans[i]; if(ans[key]>='5') s=add(s,"1"); cout<<s; return 0;}E.宝石组合
整体思路(当然考试时候我肯定是没想出来):
由最小公倍数和最大公约数的性质我们可以推出S的值就等于三个数的最大公约数gcd(h[a],h[b],h[c])当三个数的最大公约数最大时,s最大,然后把包含此因子的三个最小数输出即可//最大公约数int gcd(int a,int b){ return b==0?a:gcd(b,a%b);}//最小公倍数int lcm(int a,int b){ return a*b/gcd(a,b);}暴力:
#include<iostream>#include<algorithm>using namespace std;typedef long long ll;const int N=1e5+5;int n,h[N],ans[5],res[5],temp=0;int gcd(int a,int b){ return b==0?a:gcd(b,a%b);}int gcd3(int a,int b,int c){ return gcd(gcd(a,b),c);}void dfs(int x,int startt) { if(x>3){ int y=gcd3(h[ans[1]],h[ans[2]],h[ans[3]]); if(y>temp){ res[1]=ans[1],res[2]=ans[2],res[3]=ans[3]; temp=y; } return ; } for(int i=startt;i<=n;i++){ ans[x]=i; dfs(x+1,i+1); ans[x]=0; }}int main(){ cin>>n; for(int i=1;i<=n;i++) cin>>h[i]; dfs(1,1); h[1]=h[res[1]],h[2]=h[res[2]],h[3]=h[res[3]]; sort(h+1,h+4); cout<<h[1]<<" "<<h[2]<<" "<<h[3]<<endl; return 0;}
优化思路(AC):
#include<iostream>#include<algorithm>#include<vector>#include<cmath>using namespace std;const int N=1e5+5;int n,h[N];vector<int>ans[N];int main(){ cin>>n; for(int i=0;i<n;i++) cin>>h[i]; sort(h,h+n); //遍历一遍把数放入其因子中 for(int i=0;i<n;i++){ for(int j=1;j<=sqrt(h[i]);j++){ if(h[i]%j==0){ ans[j].push_back(h[i]); if(h[i]/j!=j) ans[h[i]/j].push_back(h[i]); } } } //从最大的因子开始遍历,个数不低于3就可以输出 for(int i=N-1;i>=0;i--){ if(ans[i].size()>=3){ cout<<ans[i][0]; for(int j=1;j<3;j++){ cout<<" "<<ans[i][j]; } break; } } return 0;}F.数字接龙
这题考试时候没想明白如何判断路径是否交叉,就只会dfs出所有答案可能的情况,折腾将近一个小时还没解决,最后无奈提交了样例还有-1这个情况...
实际上对于斜方向进行判断时,只需判断对于斜边的两个坐标是否被选中(AC):
#include<iostream>#include<string>using namespace std;int n,k,a[15][15],endd=0;bool flag[15][15];int dx[8]={-1,-1,0,1,1,1,0,-1};int dy[8]={0,1,1,1,0,-1,-1,-1};string ans;//寻找方向函数int direction(int x,int y){ if(a[x][y]==k-1) return 0; else return a[x][y]+1;}//回溯字符串函数string delete_last(string s){ if(s.size()==1) return "";//注意:大小为1时返回空 string temp=""; for(int i=0;i<=s.size()-2;i++) temp+=s[i]; return temp;}//核心函数dfsvoid dfs(int x,int y){ flag[x][y]=true; if(x==n&&y==n&&ans.size()==n*n-1){ cout<<ans<<endl; //只要找到字典序最小的,找到后标记endd endd++; return ; } int dir=direction(x,y); for(int i=0;i<=7;i++){ int xx=x+dx[i],yy=y+dy[i]; if(xx>=1&&xx<=n&&yy>=1&&yy<=n&&a[xx][yy]==dir&&flag[xx][yy]==false){ //判断斜方向情况,i才是真正的方向,direction只是方向的值 if(i==1&&flag[x-1][y]&&flag[x][y+1]) continue; else if(i==3&&flag[x][y+1]&&flag[x+1][y]) continue; else if(i==5&&flag[x+1][y]&&flag[x][y-1]) continue; else if(i==7&&flag[x-1][y]&&flag[x][y-1]) continue; else{ flag[xx][yy]=true; ans+=to_string(i); dfs(xx,yy); //在回溯时,特判一下已经找到答案的情况 if(endd) return ; //回溯 flag[xx][yy]=false; ans=delete_last(ans); } } } return ;}int main(){ cin>>n>>k; //注意:k的值不可能大于pow(n,2) if(k>n*n){ puts("-1"); return 0; } for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>a[i][j]; dfs(1,1); //利用endd标记是否成功dfs if(!endd) puts("-1"); return 0;}G.爬山
这题利用STL的优先队列进行模拟,考试时候魔法一和魔法二相同时候的情况没完善明确,因此下面这段代码肯定会有问题,但考完试我隐约记得while(m--)好像被我写成了while(n--),我真是个**:
#include<iostream>#include<cmath>#include<queue>using namespace std;typedef long long ll;const int N=1e5+5;int n,p,q,h[N];ll ans;priority_queue<int,vector<int>,less<int>>pq;int magic(int x){ int a=sqrt(x); int b=x/2; if(a>b) return 2; else if(a<b) return 1; else return 0;}int main(){ cin>>n>>p>>q; for(int i=1;i<=n;i++){ int x; cin>>x; pq.push(x); } int m=p+q; while(m--){ int t=pq.top(); pq.pop(); if(p>0&&q>0){ int tt=magic(t); if(tt==0){ if(q>p) pq.push(t/2),q--; else pq.push((int)sqrt(t)),p--; } else if(tt==1){ pq.push((int)sqrt(t)); p--; } else{ pq.push(t/2); q--; } } else if(p>0&&q<=0){ pq.push((int)sqrt(t)),p--; } else if(q>0&&p<=0){ pq.push(t/2),q--; } else{ break; } } while(pq.size()){ ans+=pq.top(); pq.pop(); } cout<<ans<<endl; return 0;}
HACK数据:
2 1 149 48H.拔河
这题考试时候直接理解错题目了(哭),以为每一人都要参加拔河,估计直接零蛋了haha
所以做题时一定要认真把题目读清楚...
暴力枚举两个连续区间的左右端点:
#include<iostream>using namespace std;typedef long long ll;const int N=1e3+5;ll n,a[N],l1,r1,l2,r2,ans=1e18;//不开浪浪见祖宗...int main(){ cin>>n; for(int i=1;i<=n;i++){//前缀和 cin>>a[i]; a[i]+=a[i-1]; } for(int l1=1;l1<=n;l1++){ for(int r1=1;r1<=n;r1++){ for(int l2=1;l2<=n;l2++){ for(int r2=1;r2<=n;r2++){ if(l1<=r1&&r1<l2&&l2<=r2){ ll sum1=a[r1]-a[l1-1]; ll sum2=a[r2]-a[l2-1]; ans=min(ans,abs(sum2-sum1)); } } } } } cout<<ans<<endl; return 0;}
前缀和+multiset(AC):
#include<iostream>#include<set>using namespace std;typedef long long ll;const int N=1e3+5;ll n,a[N],ans=1e18;multiset<ll>s;int main(){ cin>>n; for(int i=1;i<=n;i++){ cin>>a[i]; a[i]+=a[i-1]; } //利用multiset(有序并且可以重复)记录所有可能的区间 for(int l=1;l<=n;l++) for(int r=1;r<=n;r++) if(r>=l) s.insert(a[r]-a[l-1]); //枚举左区域的右端点 for(int r=1;r<n;r++){ //删除以r为左端点的所有区间,因为接下来右区间是从r+1开始选择 //如果保留之前的以r为左端点的右区间之和,会影响答案 for(int i=r;i<=n;i++) s.erase(s.find(a[i]-a[r-1])); //枚举左区间的左端点 for(int l=1;l<=r;l++){ //计算左区间 ll temp=a[r]-a[l-1]; auto x=s.lower_bound(temp); //multiset.lower_bound(key)函数返回一个迭代器 //返回第一个>=key的元素 //如果key>容器max,则返回当前容器中最后一个元素的位置 if(x!=s.end()){ ans=min(ans,abs(*x-temp));//和temp右侧的*x更新ans } if(x!=s.begin()){ x--;//先向左移动x ans=min(ans,abs(*x-temp));//和temp左侧的*x更新ans } } } cout<<ans<<endl; return 0;}