

登神长阶
上古神器-常见排序算法
冒泡排序/快速排序/归并排序/非基于比较排序
?一.前言
为保障知识获取的可读性,以及连贯性,再开始可以适当的重新温习前文内容 :Java 【数据结构】常见排序算法实用详解(上) 插入排序/希尔排序/选择排序/堆排序【贤者的庇护】
在本篇内容我们将紧跟前篇内容,进一步学习冒泡排序,快速排序,归并排序以及非基于比较排序。
?二.冒泡排序
基本原理
冒泡排序是一种简单直观的排序算法,它重复地遍历要排序的列表,一次比较两个元素,并且如果它们的顺序错误就将它们交换位置。这个过程持续到列表没有任何再次交换的元素为止。
算法步骤
从列表的第一个元素开始,依次比较相邻的两个元素。如果顺序不正确(例如,前面的元素大于后面的元素),则交换这两个元素。继续对每一对相邻元素进行相同的操作,直到到达列表的末尾。重复以上步骤,每次都从列表的开始处进行,直到没有任何元素需要交换。时间复杂度
冒泡排序的时间复杂度为O(n^2),其中n是列表的长度。这是因为在最坏情况下,需要进行n-1轮比较,每一轮最多进行n-1次交换。
稳定性
冒泡排序是稳定的排序算法。在排序过程中,相同元素的相对位置不会发生变化,只有在相邻元素大小不同时才进行交换。
适用性
冒泡排序是一个简单但效率较低的排序算法,通常用于教学目的或者在数据集较小时。由于其时间复杂度较高,在大型数据集上性能不佳,不适合实际应用。然而,由于其实现简单,易于理解和实现,有时在一些特殊场景下可能会被采用。
源代码
/** * 冒泡排序 * 时间复杂度: * 不管数据 有序 还是无序 在不优化的情况下:O(N^2) 5 4 3 2 1 * 空间复杂度:O(1) * 稳定性:稳定 * 目前学到现在为止:2个稳定排序 ,插入排序 冒泡排序 * @param arr */ public static void bubbleSort(int[] arr){ for (int i = 0; i < arr.length-1; i++) { boolean flag=false; for (int j = 0; j < arr.length-i-1; j++) { if (arr[j]>arr[j+1]){ swap(arr,j,j+1); flag=true; } } //在优化了的情况下,当数据有序,1 2 3 4 5 //时间复杂度为:O(N) if (flag==false){ break; } } }?三.快速排序
基本原理
快速排序是一种基于分治思想的排序算法。它的基本思想是选择一个基准元素,然后将数组分割成两个子数组,一个子数组中的所有元素都比基准元素小,另一个子数组中的所有元素都比基准元素大。然后递归地对这两个子数组进行排序。
算法步骤
选择一个基准元素(通常是数组中的第一个元素)。将数组分割成两个子数组,一个子数组中的元素都比基准元素小,另一个子数组中的元素都比基准元素大。递归地对两个子数组进行排序。将两个排序好的子数组合并起来。时间复杂度
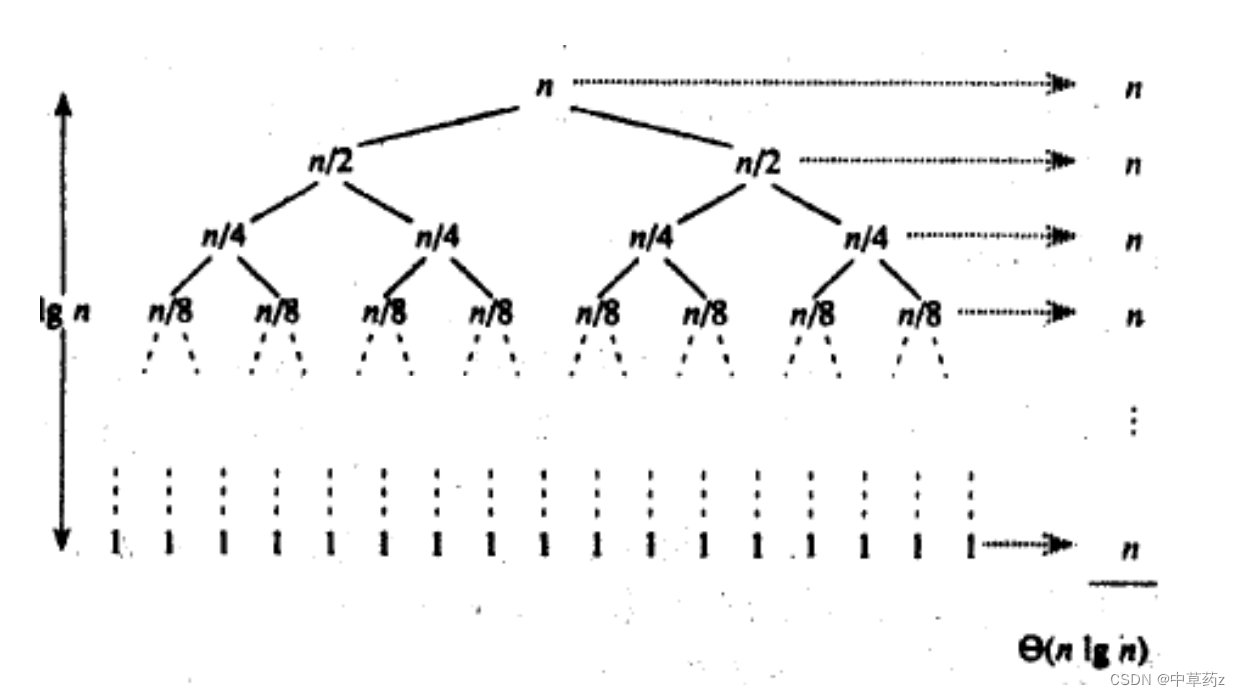
快速排序的平均时间复杂度为O(n log n),其中n是数组的长度。最坏情况下的时间复杂度是O(n^2),当数组已经有序或者基准元素选择不当时会发生。然而,由于快速排序通常表现良好,因此平均时间复杂度更具代表性。
稳定性
快速排序是不稳定的排序算法。在排序过程中,相同元素的相对位置可能会发生变化。
适用性
快速排序在大多数情况下表现良好,并且通常被认为是最快的排序算法之一(因此得名)。它特别适用于大型数据集的排序,因为其平均时间复杂度相对较低。然而,由于其不稳定性和最坏情况下的性能可能较差,有时可能不适用于特定情况,例如需要稳定排序的场景。
源代码
/** * 快速排序 * 时间复杂度:O(N*logN) * 空间复杂度:O(logN) * 稳定性:不稳定 * @param array */public static void quickSort(int arr[]){//保证接口的统一性 quick(arr,0,arr.length-1); } public static void quick(int[] arr,int start,int end){ if (start>=end){ return; } //寻找基准元素 int par=partition(arr,start,end); quick(arr,start,par-1); quick(arr,par+1,end); }在上述代码之中, int par=partition(arr,start,end);有多种方法,在这里我们展开说明三种:
1.挖坑法
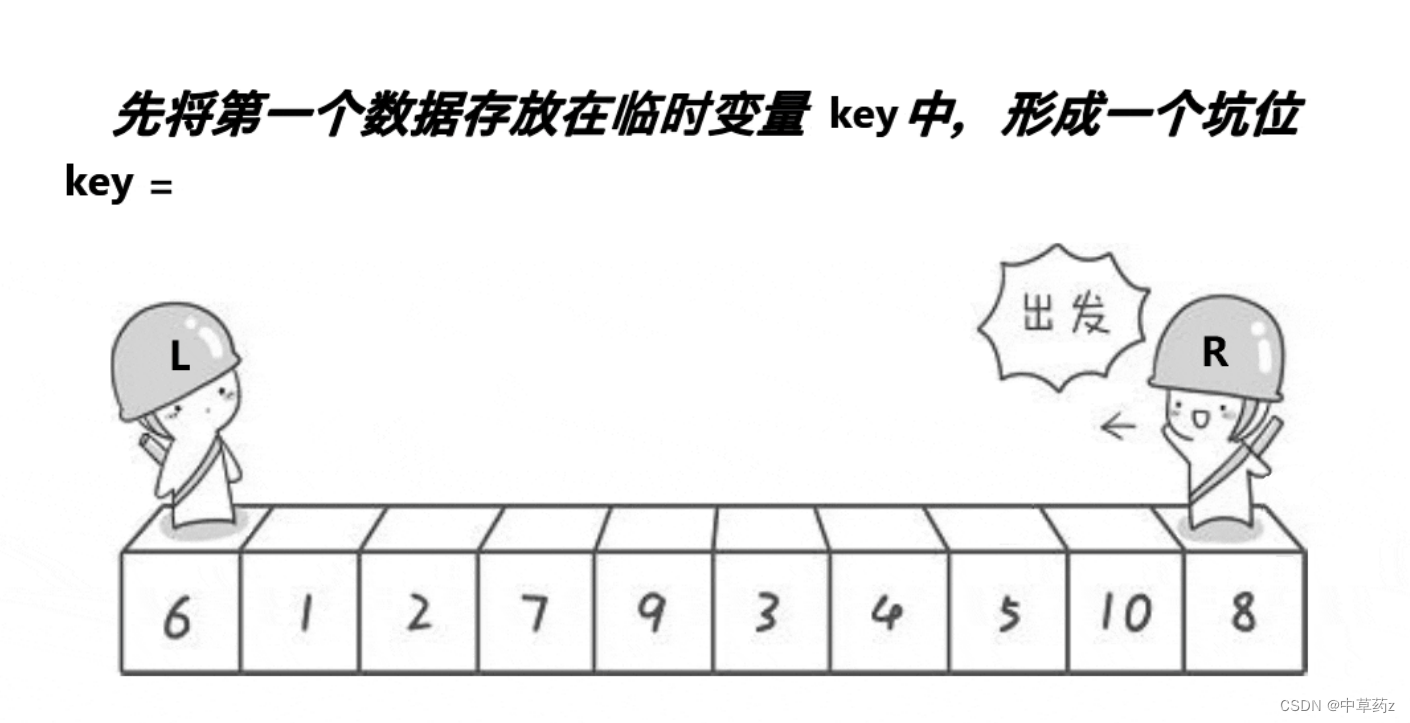
/** * 挖坑法 * @param arr * @param left * @param right * @return */ public static int partitionDig(int[] arr,int left,int right){ int temp=arr[left]; while(left<right){ while(left<right&&arr[right]>=temp){ right--; } arr[left]=arr[right]; while(left<right&&arr[left]<=temp){ left++; } arr[right]=arr[left]; } arr[left]=temp; return left; }2.Hoare法
/** * Hoare法 * @param arr * @param left * @param right * @return */ public static int partitionHoare(int[] arr,int left,int right){ int i=left; int temp=arr[left]; while(left<right){ while(left<right&&arr[right]>=temp){ right--; } while(left<right&&arr[left]<=temp){ left++; } swap(arr,left,right); } swap(arr,left,i); return left; }3.前后指针法

/** * 前后指针法 * @param arr * @param left * @param right * @return */ public static int partitionPrev(int[] arr,int left,int right){ int prev=left; int cur=left+1; while(cur<=right){ if (arr[cur]<arr[left]&&arr[++prev]!=arr[cur]){ swap(arr,cur,prev); } } swap(arr,left,prev); return prev; }同时由于当数据很少,且基本趋于有序的情况而言,我们对此代码进行优化
/** * 快速排序 优化 * 时间复杂度:O(N*logN) * 空间复杂度:O(logN) * 稳定性:不稳定 * @param array */ public static void quickSort(int arr[]){ quick(arr,0,arr.length-1); } public static void quick(int[] arr,int start,int end){ if (start>=end){ return; } //优化 if(end - start + 1 <= 10) { //插入排序 insertSortRange(arr,start,end); return; } //三数取中 int index = midThreeNum(arr,start,end); swap(arr,index,start); //寻找基准元素 int par=partitionPrev(arr,start,end); quick(arr,start,par-1); quick(arr,par+1,end); } public static void insertSortRange(int[] arr,int left,int right){ for (int i = left+1; i <= right; i++) { int temp=arr[i]; int j=i-1; for (; j >=left ; j--) { if (arr[j]>temp){ arr[j+1]=arr[j]; }else{ break; } } arr[j+1]=temp; } } /** * 三位取中 * @param arr * @param left * @param right * @return */ public static int midThreeNum(int[] arr,int left,int right){ int mid=(left+right)/2; if (arr[left]<arr[right]){ if (arr[mid]<arr[left]){ return left; }else if(arr[mid]>arr[right]){ return right; }else{ return mid; } }else{ if (arr[mid]<arr[right]){ return right; }else if(arr[mid]>arr[left]){ return left; }else{ return mid; } } }同时,我们也可以用非递归的方式去实现快速排序
/** * 非递归实现快速排序 * @param arr */ public static void quickSortnot(int[] arr){ Stack<Integer> stack=new Stack<>(); int left=0; int right=arr.length-1; int par=partitionHoare(arr,left,right); if (par>left+1){ stack.push(left); stack.push(par-1); } if (par<right-1){ stack.push(par+1); stack.push(right); } while (!stack.empty()){ right=stack.pop(); left=stack.pop(); par=partitionHoare(arr,left,right); if (par>left+1){ stack.push(left); stack.push(par-1); } if (par<right-1){ stack.push(par+1); stack.push(right); } } }?四.归并排序
基本原理
归并排序是一种基于分治思想的排序算法。它的基本原理是将待排序的数组分成两部分,分别对这两部分进行排序,然后将排好序的子数组合并成一个大的有序数组。
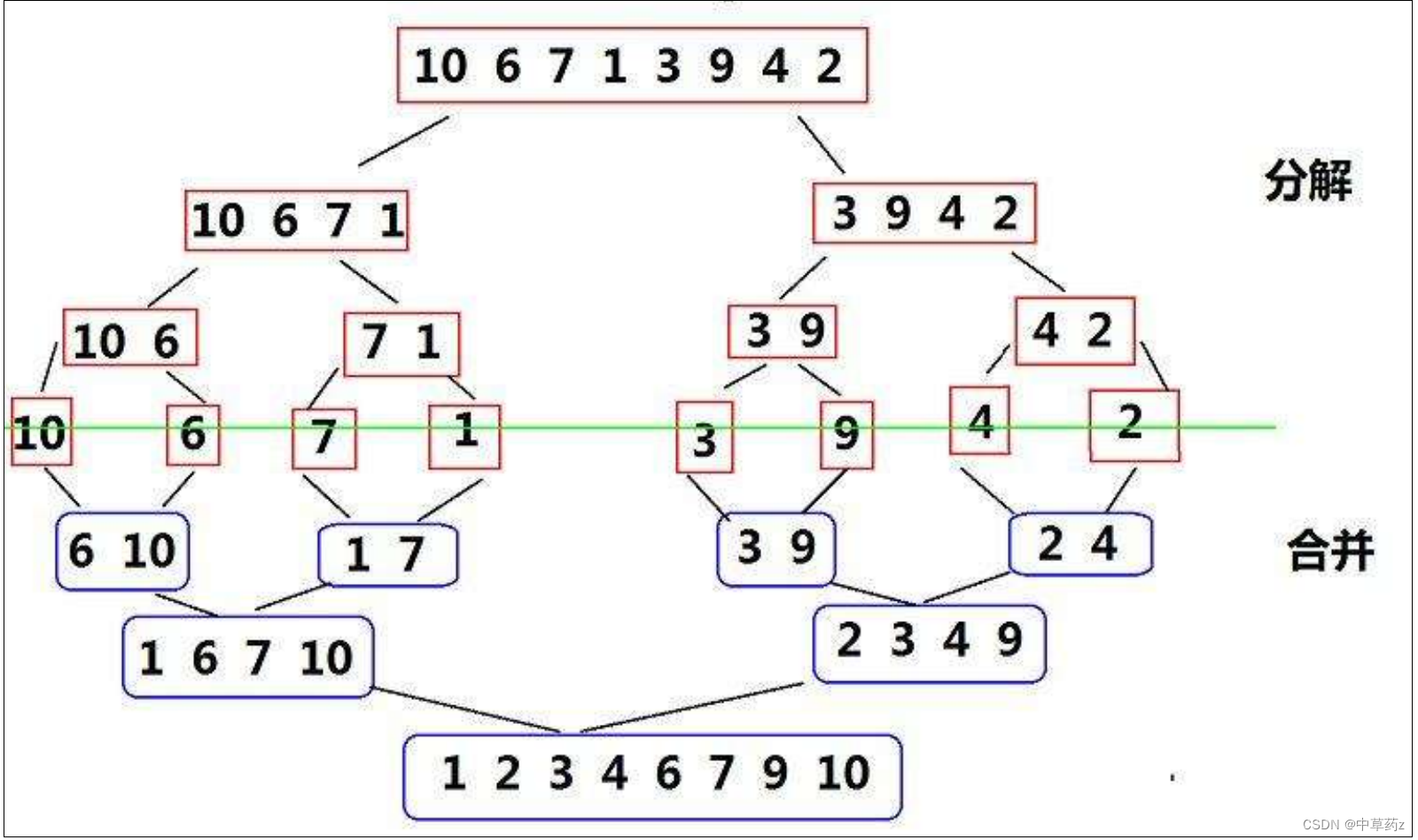
算法步骤
分解:将待排序的数组递归地分成两个子数组,直到每个子数组只有一个元素。合并:将相邻的两个子数组合并成一个有序的数组,直到整个数组被合并成一个有序的数组。时间复杂度
归并排序的时间复杂度为O(n log n),其中n是数组的长度。这是因为归并排序的每一层递归都需要O(n)的时间来合并两个子数组,而递归的深度是O(log n)。因此总的时间复杂度是O(n log n)。
稳定性
归并排序是稳定的排序算法。在合并过程中,相同元素的相对位置不会发生变化,只有在不同子数组之间的合并时才会涉及元素交换。
适用性
归并排序适用于各种数据规模的排序,尤其在内存充足的情况下,其性能稳定且良好。由于其稳定性和较好的时间复杂度,归并排序常被用于外部排序,例如对大型文件进行排序。然而,由于其需要额外的空间来存储临时数组,因此在空间复杂度较为敏感的场景下可能不适用。
源代码
/** * 归并排序 * 时间复杂度:0(N * logN) * 空间复杂度:O(N) * 稳定性:稳定的排序 * @param arr */ public static void mergeSort(int[] arr){ mergeSortfun(arr,0,arr.length-1); } public static void mergeSortfun(int[] arr,int left,int right){ if (left>=right){ return; } int mid=(left+right)/2; mergeSortfun(arr,left,mid); mergeSortfun(arr,mid+1,right); //合并 merge(arr,left,right,mid); } public static void merge(int[] arr,int left,int right,int mid){ int s1=left; int e1=mid; int s2=mid+1; int e2=right; int k=0; int[] temp=new int[right-left+1]; //要考虑相等 while(s1<=e1&&s2<=e2){ if (arr[s1]>arr[s2]){ temp[k++]=arr[s2++]; }else{ temp[k++]=arr[s1++]; } } while(s1<=e1){ temp[k++]=arr[s1++]; } while(s2<=e2){ temp[k++]=arr[s2++]; } //至此,temp数组中的所有元素已然有序 //接下来把tmp数组的内容 拷贝到array数组当中 //最后k=temp.length for (int i = 0; i < k; i++) { arr[i+left]=temp[i]; } }同理可得,可用非递归的方式去实现归并排序:
public static void mergeSortnor(int[] arr){ int gap=1; while(gap< arr.length){ for (int i = 0; i < arr.length; i=i+gap*2) { int left=i; int mid=left+gap-1; if (mid>=arr.length){ mid=arr.length-1; } int right=mid+gap; if (right>=arr.length){ right=arr.length-1; } merge(arr,left,right,mid); } gap*=2; } }?五.常用排序算法复杂度及稳定性分析
我们可以对上述接触到的排序算法进行一个简单的分类

| 排序方法 | 最好 | 平均 | 最坏 | 空间复杂度 | 稳定性 |
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 希尔排序 | O(n) | O(n^1.3) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(1) | 不稳定 |
| 快速排序 | O(n * log(n)) | O(n * log(n)) | O(n^2) | O(log(n)) ~ O(n) | 不稳定 |
| 归并排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(n) | 稳定 |
在时间复杂度方面,快速排序、堆排序和归并排序是最快的,它们的时间复杂度都是 O(n log n),适用于大多数场景。而插入排序、希尔排序、选择排序和冒泡排序的时间复杂度都在O(n^2)级别,适用于小规模数据或者教学目的。
在稳定性方面,插入排序、归并排序和冒泡排序是稳定的排序算法,而希尔排序、选择排序、堆排序和快速排序是不稳定的排序算法。稳定性表示相同元素的相对位置是否在排序前后保持不变。
在空间复杂度方面,除了归并排序需要额外的O(n)空间来存储临时数组外,其他排序算法的空间复杂度都是常数级别的,即O(1)。
? 六.其他非基于比较排序(了解)
?1.计数排序
基本原理
计数排序是一种非比较性的排序算法,其基本原理是统计待排序序列中每个元素的出现次数,然后根据元素的值将其放置到正确的位置上。计数排序假设待排序的元素都是整数,并且范围在一个已知的区间内。
算法步骤
统计计数: 遍历待排序的数组,统计每个元素出现的次数,并将统计结果存储在一个辅助数组中。累加计数: 将统计数组中的元素累加,得到每个元素在排序后的数组中的位置。排序: 遍历待排序的数组,根据统计数组中每个元素的值,将元素放置到排序后的数组中相应的位置上。输出: 将排序后的数组输出作为排序结果。时间复杂度
计数排序的时间复杂度为O(n + k),其中n是待排序数组的长度,k是待排序数组中元素的取值范围。在最坏情况下,即元素都是相同的,也需要进行n次遍历,因此时间复杂度为O(n)。而在元素范围较大的情况下,k会对时间复杂度产生影响,但通常情况下k远小于n,所以计数排序的时间复杂度可以近似看作是线性的。
稳定性
计数排序是稳定的排序算法。在排序过程中,相同元素的相对位置不会发生变化,只有根据元素的值进行元素的移动。
适用性
计数排序适用于元素取值范围较小,且待排序数组长度较大的情况。由于计数排序不涉及元素之间的比较,因此在某些情况下,它比基于比较的排序算法效率更高。然而,需要注意的是,计数排序需要额外的空间来存储统计数组,因此在元素范围非常大的情况下可能会占用过多内存。
源代码
/** * 计数排序 * 时间复杂度:O(N+范围) * 空间复杂度:O(范围) * 稳定性:稳定 * @param array */ public static void countSort(int[] array) { //1. 遍历数组 求最大值 和 最小值 int maxVal = array[0]; int minVal = array[0]; for (int i = 0; i < array.length; i++) { if(maxVal < array[i]) { maxVal = array[i]; } if(minVal > array[i]) { minVal = array[i]; } } //2. 定义count数组 int[] count = new int[maxVal - minVal + 1]; //3. 遍历array数组 把值 放入 计数数组当中 for (int i = 0; i < array.length; i++) { int val = array[i];//98 count[val - minVal]++; } //4. 以上3步完成之后,计数数组 已经存好了对应的数据 // 接下来 开始遍历 计数数组 int index = 0;//array的下标 for (int i = 0; i < count.length; i++) { while (count[i] > 0) { array[index] = i+minVal; index++; count[i]--; } } }?2.基数排序
基数排序(Radix sort)是一种非比较型整数排序算法,它的基本原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。基数排序可以采用最低有效数字(LSD)或最高有效数字(MSD)的方式进行排序。
算法步骤
确定排序的位数,即确定需要比较的最大位数。初始化10个桶(0-9),用于存放待排序的数字。从最低位开始,将所有数字按照当前位的值放入对应的桶中。将所有桶中的数字依次取出,按照桶的顺序重新排列原始数组。重复步骤3和步骤4,直到所有位都被比较完毕。时间复杂度
基数排序的时间复杂度取决于待排序数字的位数和桶的数量。如果有n个数字,每个数字有d位,基数排序的时间复杂度为O(d*n)。稳定性方面,基数排序是稳定的排序算法,即相等元素的相对顺序在排序前后保持不变。
适用性
待排序的数字是整数类型,且位数相同。待排序的数字范围不太大,可以容易地确定排序的位数。可以使用辅助空间来存储桶和中间结果。总结起来,基数排序是一种非比较型整数排序算法,通过按位数切割和桶的分配来实现排序。它具有稳定性和适用性的优点,并且时间复杂度与待排序数字的位数和桶的数量相关。
以下是动图演示

源代码
/** * 基数排序 * 考虑负数的情况还可以参考: https://code.i-harness.com/zh-CN/q/e98fa9 */public class RadixSort implements IArraySort { @Override public int[] sort(int[] sourceArray) throws Exception { // 对 arr 进行拷贝,不改变参数内容 int[] arr = Arrays.copyOf(sourceArray, sourceArray.length); int maxDigit = getMaxDigit(arr); return radixSort(arr, maxDigit); } /** * 获取最高位数 */ private int getMaxDigit(int[] arr) { int maxValue = getMaxValue(arr); return getNumLenght(maxValue); } private int getMaxValue(int[] arr) { int maxValue = arr[0]; for (int value : arr) { if (maxValue < value) { maxValue = value; } } return maxValue; } protected int getNumLenght(long num) { if (num == 0) { return 1; } int lenght = 0; for (long temp = num; temp != 0; temp /= 10) { lenght++; } return lenght; } private int[] radixSort(int[] arr, int maxDigit) { int mod = 10; int dev = 1; for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) { // 考虑负数的情况,这里扩展一倍队列数,其中 [0-9]对应负数,[10-19]对应正数 (bucket + 10) int[][] counter = new int[mod * 2][0]; for (int j = 0; j < arr.length; j++) { int bucket = ((arr[j] % mod) / dev) + mod; counter[bucket] = arrayAppend(counter[bucket], arr[j]); } int pos = 0; for (int[] bucket : counter) { for (int value : bucket) { arr[pos++] = value; } } } return arr; } /** * 自动扩容,并保存数据 * * @param arr * @param value */ private int[] arrayAppend(int[] arr, int value) { arr = Arrays.copyOf(arr, arr.length + 1); arr[arr.length - 1] = value; return arr; }}? 3.桶排序
桶排序(Bucket sort)是一种非比较型的排序算法,它将待排序元素分为若干个区间(桶),然后将每个元素放入对应的桶中。每个桶内部使用其他排序算法(如插入排序)进行排序,最后按照桶的顺序依次输出各个桶中的元素。
基本原理:
确定桶的数量,可以根据待排序元素的范围和分布情况灵活设定。将待排序元素依次放入对应的桶中。对每个桶中的元素进行排序,可以选择其他排序算法。按照桶的顺序依次输出各个桶中的元素,即得到有序序列。算法步骤:
初始化桶和空数组,桶的数量根据待排序元素范围和分布情况确定。遍历待排序元素,将每个元素放入对应的桶中。对每个桶中的元素进行排序,可以使用插入排序等其他排序算法。按照桶的顺序,将各个桶中的元素依次取出放入空数组中。输出空数组,即得到有序序列。时间复杂度: 桶排序的时间复杂度取决于元素的分布情况和桶的数量。在最均匀的情况下,平均时间复杂度和最佳时间复杂度均为O(n + k),其中n为元素个数,k为桶的数量。但在最差情况下,如果元素全部落在同一个桶中,则时间复杂度为O(n^2)。需要注意的是,桶排序的时间复杂度与元素大小无关。
稳定性:
桶排序是一种稳定的排序算法,即相等元素的相对顺序在排序前后保持不变。这是因为在将元素放入桶及桶内部排序时,采用了稳定的排序算法,如插入排序。
适用性:
待排序元素是均匀分布的。可以确定合适的桶的数量,以尽量减少桶之间元素的差距。桶内部的排序算法具有较高的效率。源代码
public static void bucketSort(int[] arr){ // 计算最大值与最小值 int max = Integer.MIN_VALUE; int min = Integer.MAX_VALUE; for(int i = 0; i < arr.length; i++){ max = Math.max(max, arr[i]); min = Math.min(min, arr[i]); } // 计算桶的数量 int bucketNum = (max - min) / arr.length + 1; ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum); for(int i = 0; i < bucketNum; i++){ bucketArr.add(new ArrayList<Integer>()); } // 将每个元素放入桶 for(int i = 0; i < arr.length; i++){ int num = (arr[i] - min) / (arr.length); bucketArr.get(num).add(arr[i]); } // 对每个桶进行排序 for(int i = 0; i < bucketArr.size(); i++){ Collections.sort(bucketArr.get(i)); } // 将桶中的元素赋值到原序列int index = 0;for(int i = 0; i < bucketArr.size(); i++){for(int j = 0; j < bucketArr.get(i).size(); j++){arr[index++] = bucketArr.get(i).get(j);}} }总结:桶排序是一种非比较型的排序算法,通过将元素放入对应的桶中,并对每个桶内部进行排序,最后按照桶的顺序输出得到有序序列。它的时间复杂度取决于元素的分布情况和桶的数量,稳定性较高,并适用于元素均匀分布的情况。
?七.总结与反思
人的成长要接受四个方面的教育:父母、老师、书籍,社会。有趣的是,后者似乎总是与前面三种背道而驰。
在学习了冒泡排序、快速排序、归并排序以及基于非比较的排序算法之后,我们可以对这些排序算法进行总结和反思。
冒泡排序
冒泡排序是一种简单的排序算法,其基本思想是将相邻的元素两两比较,如果前一个元素大于后一个元素,则交换这两个元素的位置。通过多次遍历整个数组,每次都将最大的元素"浮"到数组的末尾,从而实现排序。时间复杂度为O(n^2),不适用于大规模数据的排序。
快速排序
快速排序是一种高效的排序算法,其基本思想是选择一个基准值,将数组分为左右两部分,使得左半部分的所有元素小于等于基准值,右半部分的所有元素大于等于基准值,然后递归地对左右两部分排序。由于采用了分治的思想,并且在平均情况下时间复杂度为O(nlogn),因此快速排序是常用的排序算法之一。
归并排序
归并排序是一种稳定的排序算法,其基本思想是将待排序序列不断划分成更小的子序列,直到每个子序列只有一个元素,然后再将相邻的子序列合并成一个有序序列。由于采用了分治的思想,并且时间复杂度始终为O(nlogn),因此归并排序也是常用的排序算法之一。
非基于比较的排序算法
非基于比较的排序算法不需要进行元素之间的比较,因此它们常常具有线性的时间复杂度,但是空间复杂度较高。这类算法包括计数排序、桶排序和基数排序等。
总体来说,不同的排序算法适用于不同的场景,我们需要根据具体的问题和数据特点选择合适的排序算法。同时,我们还应该注意算法的时间复杂度、稳定性和空间复杂度等方面,以便在实际应用中能够达到更好的效果。
????????????????????????????
以上,就是本期的全部内容啦,若有错误疏忽希望各位大佬及时指出?
制作不易,希望能对各位提供微小的帮助,可否留下你免费的赞呢?