【论文导读】- Subgraph Federated Learning with Missing Neighbor Generation（FedSage、FedSage+）

文章目录

论文信息摘要FedSageSubgraphs Distributed in Local Systems孤立子图上的协作学习 FedSage+Missing Neighbor Generator (NeighGen)Graphsage和Neighgen的本地联合训练Graphsage和Neighgen的联邦学习FedSage+ Algorithm

论文信息

Subgraph Federated Learning with Missing Neighbor Generation

原文链接：Subgraph Federated Learning with Missing Neighbor Generation：https://arxiv.org/abs/2106.13430

摘要

Graphs have been widely used in data mining and machine learning due to their unique representation of real-world objects and their interactions. As graphs are getting bigger and bigger nowadays, it is common to see their subgraphs separately collected and stored in multiple local systems. Therefore, it is natural to consider the subgraph federated learning setting, where each local system holds a small subgraph that may be biased from the distribution of the whole graph. Hence, the subgraph federated learning aims to collaboratively train a powerful and generalizable graph mining model without directly sharing their graph data. In this work, towards the novel yet realistic setting of subgraph federated learning, we propose two major techniques: (1) FedSage, which trains a GraphSage model based on FedAvg to integrate node features, link structures, and task labels on multiple local subgraphs; (2) FedSage+, which trains a missing neighbor generator along FedSage to deal with missing links across local subgraphs. Empirical results on four real-world graph datasets with synthesized subgraph federated learning settings demonstrate the effectiveness and efficiency of our proposed techniques. At the same time, consistent theoretical implications are made towards their generalization ability on the global graphs.

图由于其对现实世界对象及其相互作用的独特表示，在数据挖掘和机器学习中得到了广泛的应用。随着图形越来越大，常见的看到他们的子图分别收集和存储在多个本地系统。因此，考虑子图联邦学习设置是很自然的，其中每个局部系统持有一个小的子图，这个小的子图可能会偏离整个图的分布。因此，子图联合学习旨在协作地训练一个强大的、可泛化的图挖掘模型，而无需直接共享它们的图数据。

在这项工作中，针对子图联邦学习的新颖而现实的设置，我们提出了两个主要的技术：( 1 ) FedSage，它训练了一个基于FedAvg的GraphSage模型集成多个局部子图上的节点特征、链接结构和任务标签；( 2 ) FedSage +，它沿着FedSage训练一个缺失的邻居生成器，以处理跨本地子图的缺失链接。在4个具有合成子图联邦学习设置的真实图数据集上的实验结果表明了我们提出的技术的有效性和高效性。同时，对它们在全局图上的可推广性提出了一致的理论含义。

FedSage

Subgraphs Distributed in Local Systems

我们将一个全局图表示为G = { V，E，X }，其中V是节点集，X是各自的节点特征集，E是边集。在FL系统中，我们有中心服务器S，和M个具有分布式子图的数据拥有者。Gi = { Vi，Ei，Xi }是Di拥有的子图，其中i∈[ M ]。

对于整个系统，我们假设。为了模拟链路缺失较多的场景，我们假设数据所有者之间没有重叠节点共享。注意，中心服务器S只维护一个图挖掘模型，不存储实际的图数据。任何数据拥有者Di都不能直接从另一个数据拥有者Dj中检索出u∈Vj 。

对于全局图G = { V，E，X }，每个节点v∈V都有其特征xv∈X和一个标签yv∈Y用于下游任务，例如节点分类。注意，对于v∈V，v的特征和相应的标签是一个dy -维one - hot向量。在一个典型的GNN中，预测一个节点的信息需要查询节点的自我图。对于图G中的一个节点v，我们将v的查询图表示为G ( v )，并且( G ( v )，yv ) ~ DG。

该系统利用FL框架协作地学习所有数据所有者中的孤立子图，而无需原始图数据共享，从而获得一个全局节点分类器F。F中的可学习权重φ按照从全局图G中抽取的权重的分布为查询的自我图进行优化。我们将问题形式化为寻找最小化聚合风险的φ *：

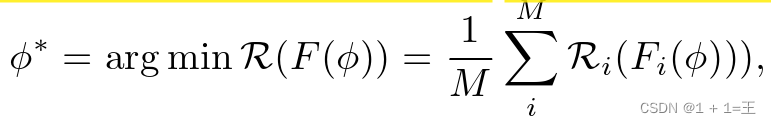
其中, Ri 是本地经验风险定义为:

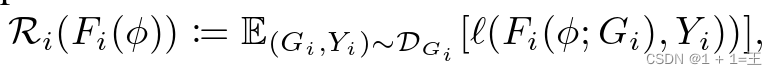
其中，l是任务特定的损失函数:

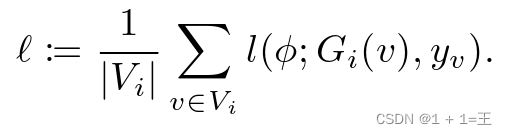
孤立子图上的协作学习

为了实现上述系统目标，我们利用简单高效的Fed Avg框架，将节点分类器F固定为Graph Sage模型。GraphSage模型的归纳性和可扩展性为训练具有异构查询分布的不同子图以及后期对全局图的推理提供了便利。我们将使用FedAvg框架训练的GraphSage模型称为FedSage。

对于一个被查询的节点v∈V，一个全局共享的K层GraphSage分类器F将v和它在图G上的K跳邻域集成起来，用可学习的参数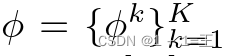进行预测。以子图Gi为例，对于特征为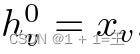的v∈Vi，在每一层k∈[ K ]上，F计算v的表示为：

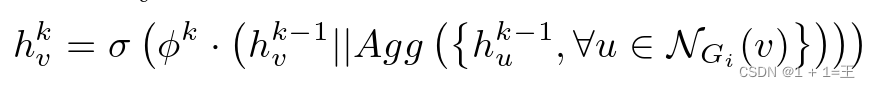
其中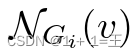，是图Gi上v的邻居的集合，|| 是串联操作，Agg(·)是聚合器，σ是激活函数。

对于v∈ViF输出推理标签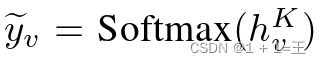 时，监督损失函数l ( φ | · )定义如下：

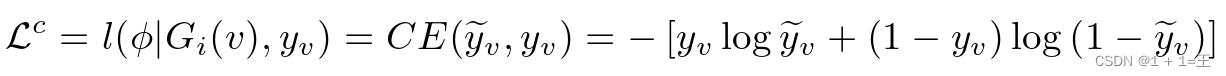
其中CE(·) 是交叉熵函数，Gi ( v )是v在Gi上的K跳自我图，它包含v及其在Gi上的K跳邻居的信息。

在Fed Sage中，分布式子图系统通过ec轮的训练得到一个由φ参数化的共享全局节点分类器F。在每个epoch t内，每个Di首先本地计算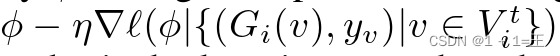，其中包含epoch t的采样训练节点，η为学习率；然后中心服务器S收集最新的；接下来，通过对进行平均，S将φ设置为平均值；最后，S向数据所有者广播φ并完成一轮训练F。在ec轮之后，整个系统检索F作为结果全局分类器，它不局限于或偏向于任何特定数据所有者中的查询。

与欧几里得数据上的FL不同，分布式子图系统中的节点可以在子图之间进行潜在的交互。然而，由于系统中的跨子图链接不能被任何数据拥有者捕获，因此与全局图上的跨子图链接相比，不完全邻域普遍存在于其中。因此，通过FedSage直接聚合不完全查询的自我图信息，限制了结果F获取全局查询分布的迫切的要求。

FedSage+

Missing Neighbor Generator (NeighGen)

NeighGen的神经架构如下图所示，Neigh Gen由编码器He和发生器Hg两个模块组成。我们在下面详细描述了它们的设计。

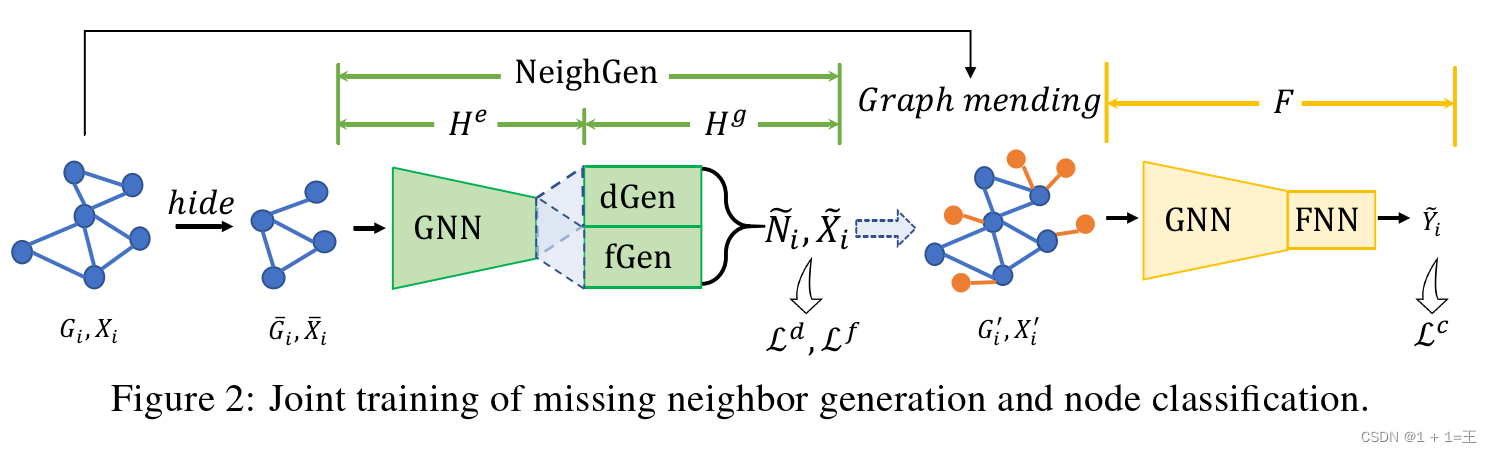
He:一个GNN模型，即K层Graph Sage编码器，参数为θ e。对于在输入图Gi上的节点v∈Vi，根据公式计算节点嵌入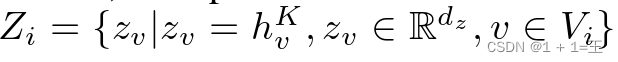Hg：一种基于节点嵌入恢复输入图缺失邻居的生成模型。Hg包含dGen和fGen，其中dGen是由θ d参数化的线性回归模型，预测缺失的邻居数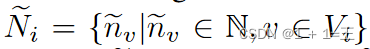，fGen是由θ f参数化的特征生成器，生成一组Ni个特征向量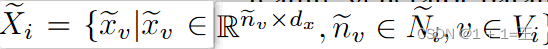。dGen和fGen都被构造成全连接神经网络( FNNs )，而fGen还配备了一个生成z维噪声向量的高斯噪声生成器N( 0 , 1)和一个随机采样器R。对于节点v∈Vi，fGen是变分的，它在将噪声插入到嵌入zv后为v生成缺失的邻居特征，而R保证fGen通过从特征生成器的输出中采样nv个特征向量来输出特定数目邻居的特征。从数学上讲，我们有

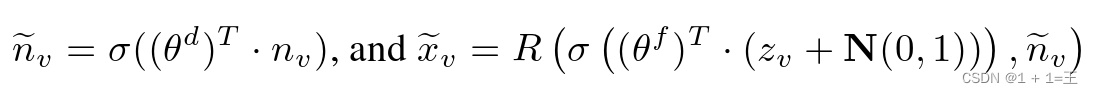
对于我们系统中的每个数据所有者，我们假设只有一组特定的节点有跨子图缺失的邻居。该假设是现实而非平凡的，因为它既抓住了分布式子图系统的本质，又允许我们通过一个图的减损和修补过程来局部模拟邻居缺失的情况。具体来说，为了模拟Neigh Gen训练过程中的图修补过程，在每个局部子图Gi中，随机保留其节点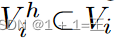的h%和所有涉及它们的链接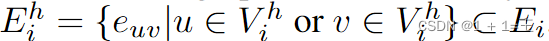，形成一个受损子图，记为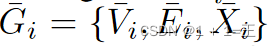包含节点受损集合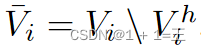，对应节点特征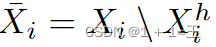和边。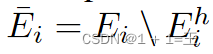

因此，基于真实缺失的节点Vhi链接Ehi，在受损的图Gi上训练NeighGen可以联合训练dGen和fGen，如下所示:

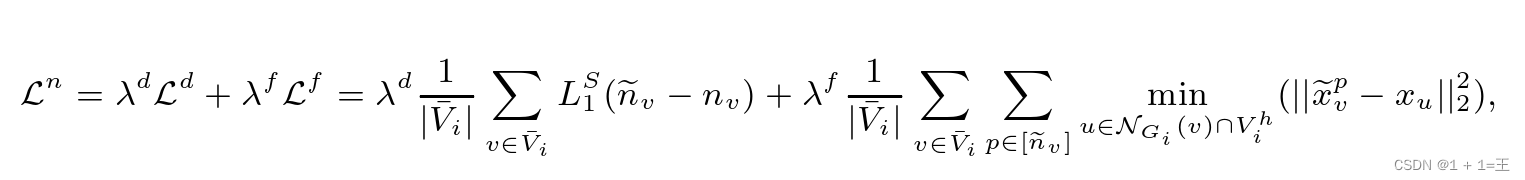
其中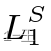是平滑的L1距离，是xv中的第p个预测特征。值得注意的是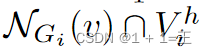包含了nv个节点，这些节点是v在Gi上的邻居节点，但不包含在Vhi中。检索到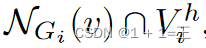为训练Neigh Gen提供了依据。

Graphsage和Neighgen的本地联合训练

虽然NeighGen旨在恢复丢失的邻居，但我们系统的最终目标是训练分类器。因此，我们设计了Graph Sage和Neigh Gen的联合训练，利用Neigh Gen生成的邻居辅助Graph Sage进行节点分类。我们将Graph Sage和Neigh Gen在局部图上的集成称为LocSage +。

Neigh Gen将图Gi修复成图Gi’后，对图Gi’应用Graph Sage分类器F。因此，NeighGen和Graph Sage的联合训练通过优化以下损失函数来完成：

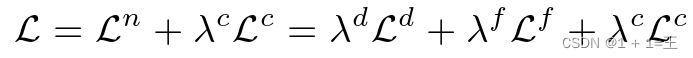
GraphSage和NeighGen的本地联合训练允许NeighGen在本地图中生成有助于GraphSage分类的缺失邻居。然而，与Graph Sage一样，局部Neigh Gen中编码的信息仅限于并偏向于局部图，并不能使其真正生成由缺失的交叉子图链接连接的属于其他数据拥有者的邻居。为此，用FL训练Neigh Gen也是很自然的。

Graphsage和Neighgen的联邦学习

类似于单独使用Graph Sage，通过将损失函数设置为L，可学习参数设置为{ θe，θd，θf，φ }，可以将FedAvg应用于Graph Sage和Neigh Gen的联合训练。然而，我们观察到通过直接平均NeighGen在整个系统中的权重来进行合作会对其性能产生负面影响，即平均单个NeighGen模型的权重并不能真正让它从不同的子图中产生不同的邻居。考虑到我们构建Neigh Gen的目标是通过在每个子图中生成不同的缺失邻居来方便训练一个集中式的Graph Sage分类器，因此我们不一定需要一个集中式的Neigh Gen。因此，我们不训练单个集中式Neigh Gen，而是为每个数据拥有者Di训练一个本地Neigh Geni。为了让每个Neigh Geni生成与其他子图Gj相似的不同邻居，我们在f Geni中添加一个跨子图特征重构损失如下：

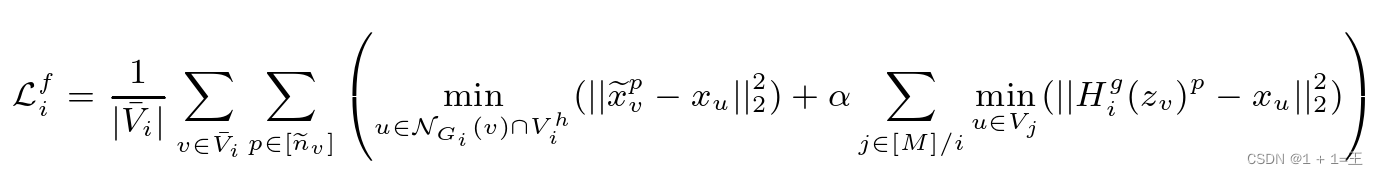
如上所示，为优化方程，Di需要从Gj中选择最接近的u。然而，将Dj中的节点特性Xj直接传输给Di不仅违反了我们的子图FL系统关于没有直接数据共享的约束，而且在现实中也是不切实际的，因为它要求每个Di在训练NeighGeni的过程中保持整个全局图的节点特性。因此，为了允许Di使用公式更新Neigh Geni。在不直接访问Xj的情况下，对于v¯∈Vi，Dj本地计算并将相应的梯度发回Di。

FedSage+ Algorithm